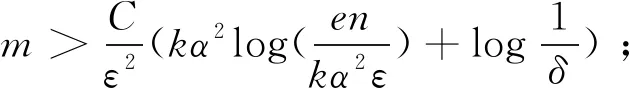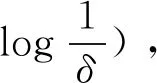通过混合l2/l1范数最小化实现块稀疏信号恢复

李 坤 王会敏

(绍兴文理学院 数理信息学院，浙江 绍兴 312000)

0 引言

压缩感知是Donoho[1]和Candese等[2]提出的一种新采样理论，该理论指出可压缩的信号可通过远低于Nyquist-Shannon Sampling Theorem[3]的标准进行采样，原始信号仍然能够被精确地恢复.在压缩感知中，利用一个观测矩阵对高维信号进行线性压缩观测得到少数的观测值，进而形成线性观测模型，根据少数的观测值和已知的观测矩阵，通过构造和求解有效的优化问题，最终实现精确或者是高概率地重构原始信号.当原始的高维信号是稀疏信号，即信号的非零元素的个数远远小于信号的维数时，可以显著减少估计所需的测量数量.

现实世界中自然信号的结构千变万化，常见的稀疏结构有块稀疏[4-5]、图稀疏[6]、树稀疏[7]等.其中最为普遍的是块稀疏信号，该信号的非零元素以块的形式出现.现有研究表明，充分利用块稀疏结构，可以进一步降低压缩感知中的数据采样率，提高数据重构效率.近年来，块稀疏信号的应用涉及多个领域，包括DNA微阵列[8]、稀疏通信均衡通道[9]、雷达成像[10]、脑磁图、多宽带信号[11]、数据挖掘、纠错编码等领域.

许多研究表明，在处理块稀疏信号时，混合l2/l1范数最小化的方法优于标准的l1范数最小化.Huang等[12]利用一个称为强群稀疏性的概念发展了混合l2/l1范数最小化的理论，证明了混合l2/l1范数最小化对于恢复强群稀疏信号是非常有效的.Stojnic等[13]通过混合l2/l1范数最小化得到了恢复块稀疏信号的最优高斯测量值.Eldar等[14]表明，在l1范数情况下，如果测量矩阵有相同的有限等距常数，那么在无噪声的情况下，混合l2/l1范数方法可以完全恢复任何块稀疏信号.

本文基于混合l2/l1范数最小化，考虑了观测模型y=Φx+ξ+d，其中Φ是高斯矩阵，‖ξ‖2,0≤ηm，得到稀疏噪声和有界噪声两个结果：

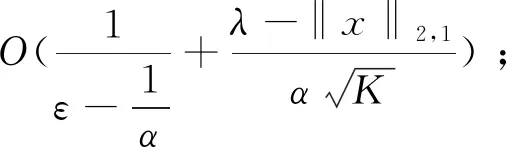
1 预备知识

设Φ∈Rm×n是一个高斯矩阵，y∈Rm为观测值，x∈Rn是块稀疏向量.设I={d1,d2,...,dn} 是分块指标集，向量x∈Rn的结构如下

(1.1)

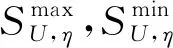
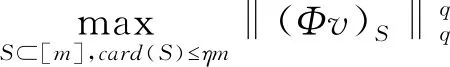
其中card(S)表示S包含的块数，则矩阵Φ∈Rm×n对U⊂Rn具有(η,b)鲁棒性.

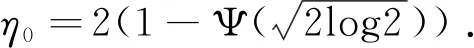
2 主要结果

在测量矩阵Φ一定的条件下，有唯一一个块稀疏信号服从y=Φx，可以通过求解混合l2/l1范数最小化问题：

(2.1)

如果测量值y有损坏，(2.1)变成了以下噪声版本：

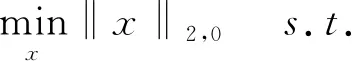
(2.2)

其中ε表示噪声误差.与标准的l0范数最小化问题类似，(2.2)是混合l2/l0范数最小化问题，是NP-hard问题.基于压缩感知的研究，通常使用混合l2/l1范数代替混合l2/l0范数，求解混合l2/l1范数最小化问题.

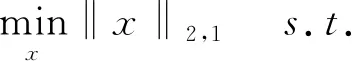
(2.3)

(2.3)是一个凸优化问题，可以重新定义为一个凸二阶锥来有效地求解.

本文在以上基础考虑，若观测矩阵Φ∈Rm×n是正态矩阵且独立同分布.考虑以下观测模型:

y=Φx+ξ+d

其中，x∈Rn为块K-稀疏信号，ξ∈Rm为块-ηm稀疏噪声向量，d∈Rm为噪声向量.以下是本文的主要结果.

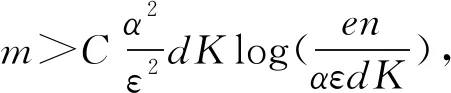
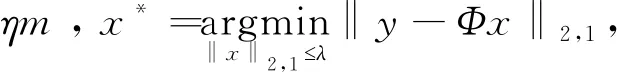
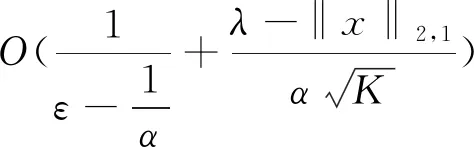
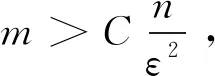
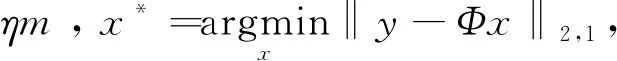
3 主要引理及证明

为了证明定理2.1，在[15]引理3.3，引理3.4的基础上，将k-稀疏信号推广至块K-稀疏信号，得到了相关引理.

引理3.1[15]设S={z1,...,zm}是通过N(0,1)采样得到，并且是独立同分布的，下列不等式

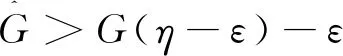
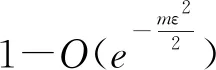
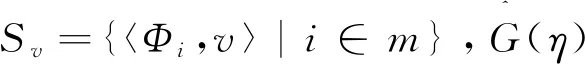
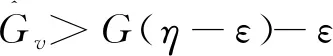
(3.1)

为了做到这一点，首先证明在球面上足够细的网中，所有块K-稀疏单位向量以很高的概率满足(3.1)，对于网外的点，(3.1)偏差不能很大.在引理3.2的基础上，定义以下事实：令v是一个固定的向量，参数τ>0，

根据卡方随机变量的性质，则有:

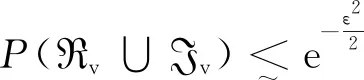
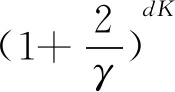
设u∈Rn为块K-稀疏单位向量.对于任何t，存在v0,v1,...,vt与u有相同的块支集，一个单位向量d也与u有相同的块支集，于是有:

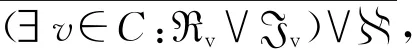
(3.2)

引理3.2证明了高斯矩阵对块K-稀疏向量具有鲁棒性.本文最终目的是证明高斯矩阵对‖x-x*‖也具有鲁棒性.在接下来的引理中，使用参数，将块(1+α2)K-稀疏向量的特征值的上界和下界转移到圆锥VS={x∈RN|Δ+‖xS‖2,1≥‖xSC‖2,1}上，其中card(S)=K.

引理3.3 对任意块(1+α2)K-稀疏向量x，A∈Rm×n满足L‖x‖2≤‖Ax‖2，1≤U‖x‖2.如果S⊂[m]，且card(S)=K，则A满足：

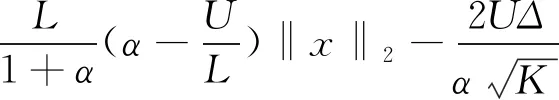
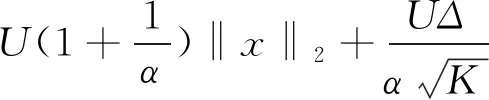
其中x∈VS={x∈RN|Δ+‖xS‖2,1≥‖xSC‖2,1}.

证明：思路是将块K-稀疏向量上A的特征值转移到VS上A的特征值.为此，首先选择VS的一个元素，并将其表示为块稀疏向量的和.对于任何x∈VS记为S，SC划分为T1,T2,...,TJ，其中Ti对应于VSC中第i个最大块l2范数的指标集.然后每个Ti被分为α2K个块，对任意i≥1都有‖xTi‖2≥‖xTi+1‖2.

下面证明集合VS中向量特征值的上界和下界.根据范数的三角形不等式，有:

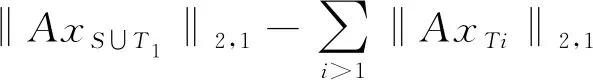
由于VS∪T1和VTi至多是块(1+α2)K-稀疏的，则:

(3.3)

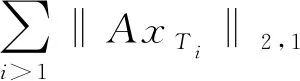
‖xTi‖2≥‖xTi+1‖2，因此

则有:

利用稀疏特征值的界，得到

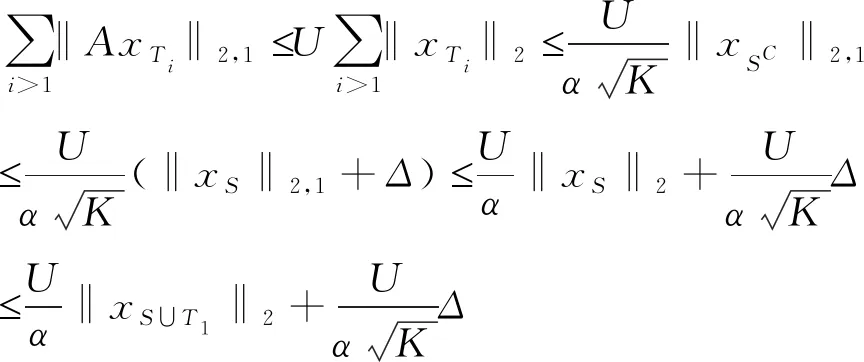
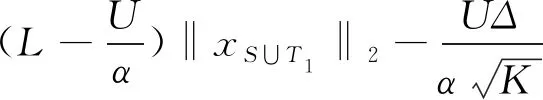
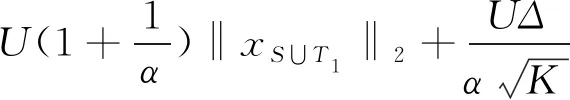
(3.4)

根据Ti的定义和柯西-施瓦茨不等式的应用，有:

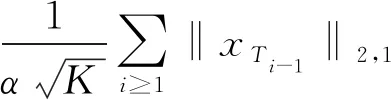
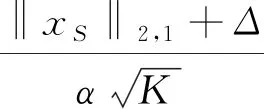
得到‖x‖2的上界:

‖x‖2≤‖xS∪T1‖2+‖x(S∪T1)C‖2

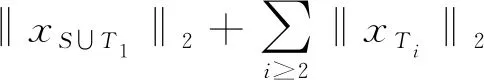
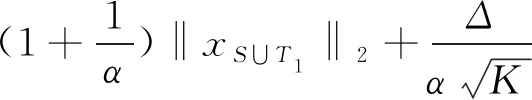
所以:

代入(3.4)，得到

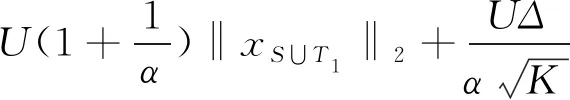
整理‖Ax‖2,1的下界，有:

得到引理:

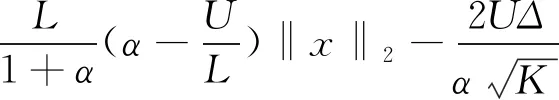
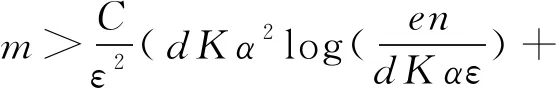
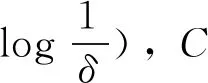
T⊂[m]且card(T)≤ηm，则下列不等式:

以1-δ的概率成立.

证明：矩阵Φ对于所有块(1+α2)K稀疏向量具有(η,1)和(1-η,1)鲁棒性.由引理3.3知，对任何矩阵A是由其行的η个分数组成，于是有以下不等式成立:

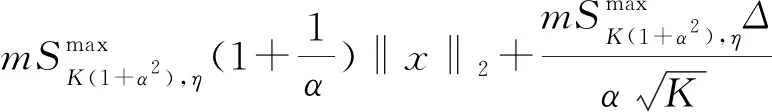
且矩阵A是Φ的子矩阵，故下列不等式成立:

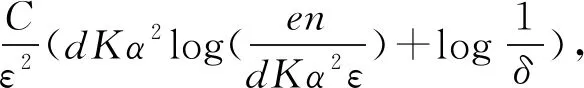
于是产生以下界限:

通过上述不等式的差值和简单化，且T⊂[m]，card(T)≤ηm，得到:

‖(Φx)TC‖2,1-‖(Φx)T‖2,1

≥m‖x‖2((G(η-ε)-B(η+ε)-2ε)-

≥m‖x‖2((G(η-ε)-B(η+ε)-2ε)-

4 主要定理的证明

利用引理3.2，3.3，3.4，开始证明本文的主要定理2.1.

令Φg和Φb分别表示Φ未损坏的行和已损坏的行，yg和yb表示对应的y项.由于，‖Φx-y‖2,1=‖Φgx-yg‖2,1+‖Φbx-yb‖2,1，故:

0≥‖Φx*-y‖2,1-‖Φx-y‖2,1

=(‖Φgx*-yg‖2,1-‖Φgx-yg‖2,1)+

(‖Φbx*-yb‖2,1-‖Φbx-yb‖2,1)

≥‖Φg(x*-x)‖2,1-2‖Φgx-yg‖2,1+

(‖Φbx*-yb‖2,1-‖Φbx-yb‖2,1)

≥‖Φg(x*-x)‖2,1-2‖Φgx-yg‖2,1-

‖Φb(x*-x)‖2,1

(4.1)

上述式子化简为:

2‖Φgx-yg‖2,1≥‖Φg(x*-x)‖2,1-

‖Φb(x*-x)‖2,1

(4.2)

令x*=x+h， 且假设S是x的块支集， 则

λ≥‖x*‖2,1=‖h+x‖2,1≥‖x‖2,1+‖hSC‖2,1-‖hS‖2,1，于是有(λ-‖x‖2,1)+‖hS‖2,1≥‖hSC‖2,1.

令Δ=(λ-‖x‖2,1)，T是引理3.4中已损坏数据指数的集合， 这意味着如果

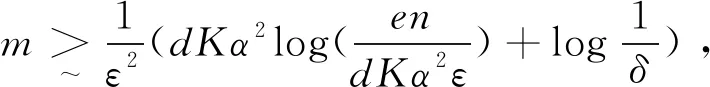
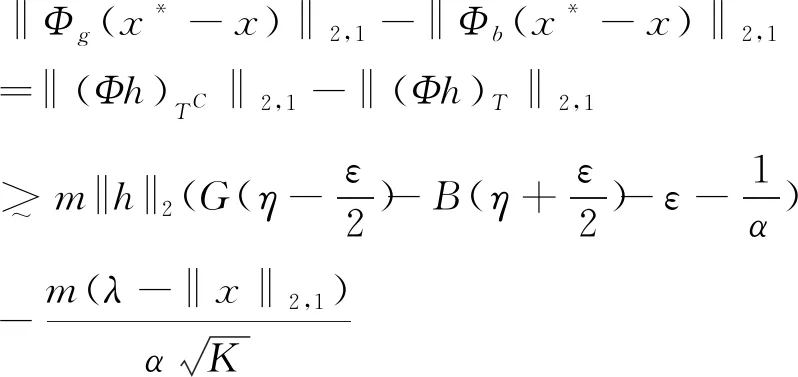
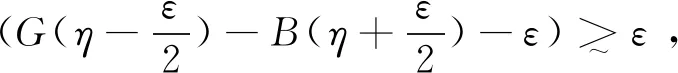
也就是:

得到的结果:

当x不是稀疏信号时，由(4.2)直接利用引理3.2即可得到定理2.2.

5 总结

对于块稀疏向量，可以在不知道原始信号中非零系数的位置坐标的情况下精确地恢复原始信号，重构过程更简单、更准确.本文利用高斯矩阵的性质得到了块K-稀疏信号最小恢复误差.若信号含有有界噪声，可直接得到‖Φx‖2,1的上下界；若信号含有块稀疏噪声，需要将x限制在锥VS={x∈RN|Δ+‖xS‖2,1≥‖xSC‖2,1}上，利用矩阵的块-RIP性质，得到‖Φx‖2,1的上下界.