岩桥倾角对岩石力学性质尺寸效应规律的影响研究

傅姜平 杜时贵，2 胡高建 马 刚

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000； 2. 宁波大学 土木与环境工程学院，浙江 宁波 315211 )

0 引言

滑坡是我国最常见的地质灾害之一，而岩质滑坡是其重要组成部分[1].对于岩质边坡应力积累使其岩桥被剪断，突发脆性破坏是其形成高速滑坡的本质原因，并且滑坡发生往往会经历“滑移-拉裂-剪断”三个过程[2].因此，研究岩桥对岩体强度特征的影响对了解岩质边坡力学性质、分析其发生机制、评估其稳定性有重要意义.

自“岩桥”概念提出以来，众多学者对其进行了相关研究.其中，针对岩桥倾角的变化，王来贵等[3]为了研究岩桥的破坏规律，通过FEPG软件进行数值模拟，认为在单轴压缩的条件下，岩桥的倾角会影响岩桥的破坏形式，并且随着岩桥倾角的增加，岩桥发生张拉破坏的概率增加；杨圣奇等[4]通过伺服试验机，研究岩桥倾角对断续三裂隙砂岩强度破坏和裂纹扩展的影响规律，得到与完整砂岩相比，从应力应变曲线上看，断续三裂隙砂岩有较大的应力跌落现象，峰值强度也明显降低，但降低程度与岩桥倾角紧密相关；韩刚[5]通过双轴压缩试验和双轴循环加卸载试验来研究岩桥的贯通模式，认为岩桥的倾角对岩桥的贯通模式有显著的影响，随着岩桥倾角的增大，岩桥的贯通模式逐渐转换为剪性或张剪性贯通；王存根等[6]基于MATLAB技术，利用FLAC3D软件进行数值模拟，认为岩桥倾角与峰值抗剪强度有关，随着岩桥倾角的增大，试样的峰值抗剪强度也呈现增大的趋势，且峰值抗剪强度的增大幅度越来越大；李玉成等[7]通过单轴压缩试验与PFC3D数值模拟相结合，认为当岩桥倾角较大时，试验和数值模拟的结果保持一致，岩桥倾角与抗压强度呈现正相关的关系.

在尺寸效应的研究上，也有不少学者做了大量的贡献.Weibull等[8]率先提出岩石强度具有尺寸效应； Carpinte等[9]引入分形方法研究岩石的尺寸效应；章仁友等[10]通过大量的实测统计分析，列举了结构面力学行为中普遍存在的尺寸效应现象,论证了结构面力学行为的尺寸效应具有分形结构；杨圣奇等[11]通过伺服试验机进行单轴压缩试验，研究尺寸对岩石强度和变形特征的影响规律，认为岩石材料的长度效应并不是非均质性所致，而是源于端部摩擦效应，并提出了大理石岩石材料的尺寸效应理论模型；吕兆兴等[12]采用数值试验的方法，研究非均质性对岩石材料尺寸效应的影响，认为尺寸效应随着非均质参数的变化而变化；张占容等[13]基于现场试验，采用数值模拟的方法，得到了不同尺寸岩体等效变形模型的变化特征；张明等[14]通过有限元软件进行数值模拟，认为不同加载条件会影响岩石强度的尺寸效应；罗战友等[15]则认为不同的边界条件会影响岩石强度的尺寸效应，对室内试验有指导意义.

综上所述，目前人们对岩桥的研究停留在揭示同一尺寸下改变岩桥倾角对岩体的破坏规律的影响，尚未有学者考虑岩桥倾角对岩体强度尺寸效应的影响.因此，本文利用RFPA[16]建立系列尺寸下含不同倾角的岩石数值模型，并通过模拟试验研究岩桥倾角对岩体单轴抗压强度及其尺寸效应的影响.

1 数值模型及实验方案

1.1 软件介绍

RFPA软件是一个能模拟岩石介质逐渐破坏过程的数值模拟工具.

为了考虑岩石是一种非均匀的材料，令基元的弹模、强度等力学参数服从韦伯分布，即

(1)

式中：m为形状参数，用来反映岩石的力学性质的均质度，m越大说明岩石越均匀；α0为用来反映岩石平均性质的参数.有关韦伯分布函数和参数定义及选取详见参考文献[8].

1.2 破坏准则

边坡岩土体作为典型的塑性材料，一般采用摩尔库伦屈服准则，在RFPA程序中，对于岩土体的破坏准则也可以采用Mohr-Coulomb屈服准则进行模拟,如图1所示.

图1 Mohr-Coulomb 模型破坏标准

τn=C+σntanφ

(2)

式中：c为土的黏聚力；φ为土的内摩擦角；σn、τn分别为滑移面上的正应力与切应力.

1.3 数值模型和试验方案

1.3.1 数值模型

文中研究预置岩桥倾角对岩石强度的影响，并通过改变试样的尺寸大小，研究岩桥倾角对岩体强度尺寸效应的影响.试样模型如图2所示，其中c为试样尺寸，α为岩桥倾角.

1.3.2 试验方案

基本的试验方案有两种，具体如下.

方案一:为了研究岩桥倾角对岩石强度的影响，试样模型如图2 所示.c 的尺寸分别为200 mm、400 mm、600 mm、800 mm 和1 000 mm，对应的α分别为15 °、30 °、45 °、60 °、75 °，共有25组模拟试验.如表1 所示.

图2 试样模型

方案二:为了研究岩桥倾角对岩石强度尺寸效应的影响，试样模型如图2所示. 倾角α 分别为15 °、 30 °、 45 °、 60 °、 75 °， 对应的c分别为200 mm、400 mm、600 mm、800 mm 和1 000 mm，共有25组模拟试验.如表1所示.

表1 岩桥长度表

模型试样均不考虑端部摩擦影响，采用摩尔库伦准则为基本的破坏准则，数值分析采用平面应力分析. 参数标定： 标定基元的平均强度为200 MPa，平均弹性模量为60 GPa，均质度为2，内摩擦角为30 °，拉压强度之比为1/10.实验过程采用竖向位移控制，每步的加载量为0.03 mm，总加载步数为100步，直至模型被压坏.

2 岩桥倾角对岩体力学行为的影响

2.1 岩桥倾角对岩体力学性质的影响

根据试验方案一，可做得岩桥倾角对岩石单轴抗压强度应力应变曲线的影响图，如图3所示.图a到图e 的模型尺寸依次为200 mm×200 mm，400 mm×400 mm，600 mm×600 mm，800 mm×800 mm，1 000 mm×1 000 mm.

a (200 mm×200 mm)

e (1 000 mm×1 000 mm)

由图3-a岩桥倾角为15 °的应力-应变曲线可知，随应变的增加，其抗压强度先增大后减小.在应变为0～0.2%时，应力应变呈现正相关关系，应力应变曲线斜率保持不变，此时，模型试样处于弹性阶段；当应变在大于0.2%以后，应力骤降，模型试样由微观上的裂纹扩展到宏观上的破坏,模型试样没有塑性阶段.对照图3-a中其余岩桥倾角的应力-应变曲线，与15 °岩桥倾角的应力应变曲线趋势相同，但不同岩桥倾角模型试样的应力应变曲线斜率不同，所达到的峰值也不同，随岩桥倾角增大，应力应变曲线的斜率逐渐减小，峰值也随之降低.故岩桥倾角的变化会影响岩石单轴抗压强度，岩桥倾角增大，岩石单轴抗压强度降低.

结合图3中a-e应力应变关系也存在上述规律.可知，当岩桥倾角从15 °变成30 °时，岩石单轴抗压强度变化幅度较小，当岩桥倾角大于30 °之后，岩石单轴抗压强度呈现明显的下降趋势，且下降的速度先增大后减小.

2.2 倾角对岩石破坏演化规律的影响

表2是尺寸为200 mm×200 mm不同岩桥倾角岩石模型的破坏过程表.

从表2可知，整个破坏过程大致分为以下几个阶段：岩石压密实阶段、节理端部出现细小裂纹阶段、贯通破坏阶段.

表2 不同岩桥倾角的破坏过程列表

下面以岩桥倾角为45 °模型的破坏过程为例.

在初始阶段，预置裂纹产生了闭合效应；在压应力的作用下，都在靠近预置裂纹内侧端部的位置出现应力集中现象；紧接着，在上部应力集中处的上方，下部应力集中处的下方，萌生了细小的裂纹，并逐渐与应力集中处的预置裂纹相连接；由于存在岩桥，在压应力的作用下，模型发生了偏转，在偏转处会集中出现大量裂纹；在压应力的进一步作用下，裂纹发育速度增加，岩桥被贯通破坏.

结合表中其余岩桥倾角，岩石模型的破坏过程也存在上述规律.但不同岩桥倾角岩石的破坏过程略微有所不同，主要是由于不同的岩桥倾角会导致受压过程中的岩石模型会在不同时刻发生偏转，且偏转的程度也有所不同.随岩桥倾角的增大，破坏过程中模型偏转的时刻前移，偏转的程度也加深.

3 岩桥倾角对岩石力学行为尺寸效应规律的影响

3.1 岩桥倾角对岩石力学行为尺寸效应规律的影响

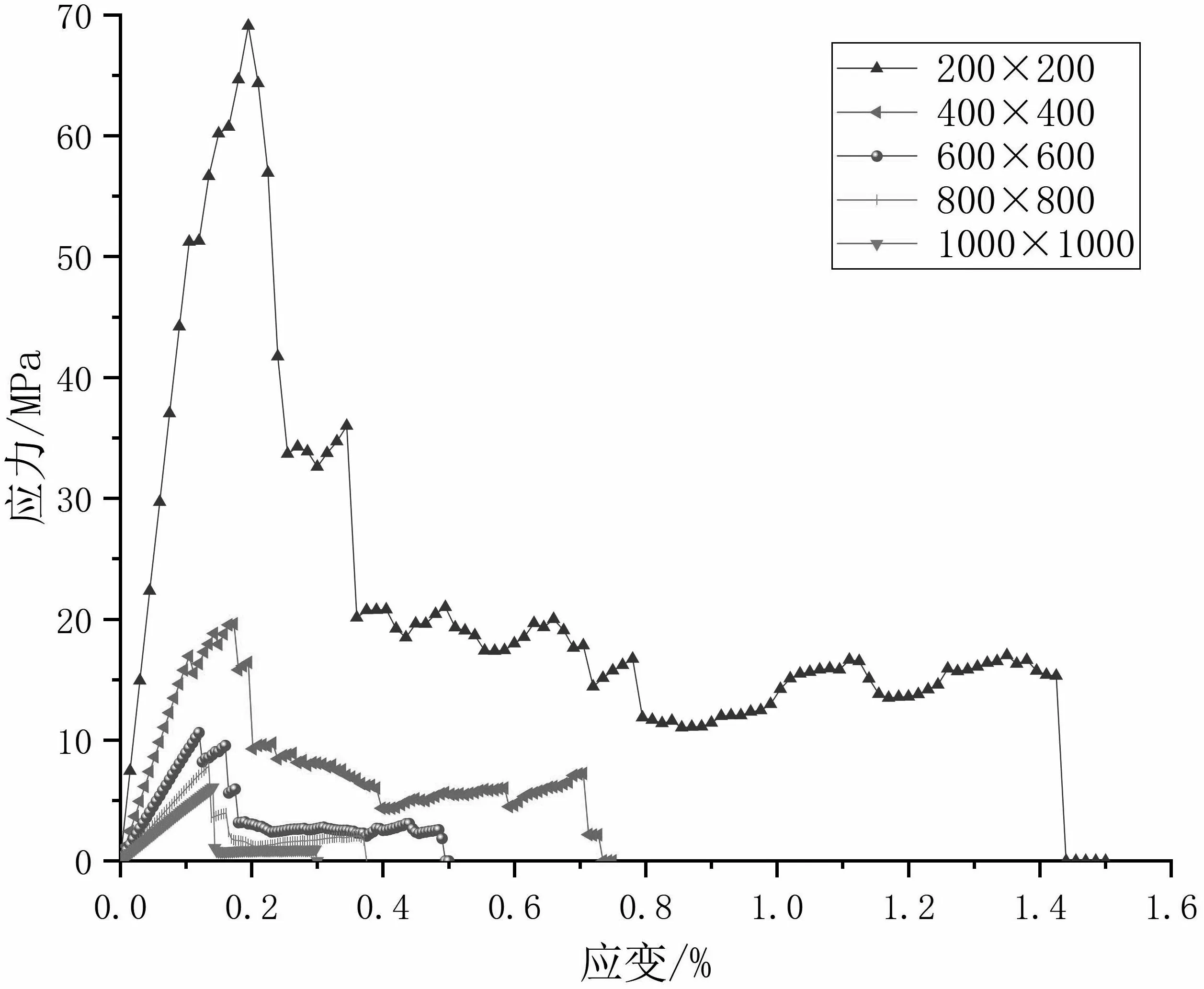
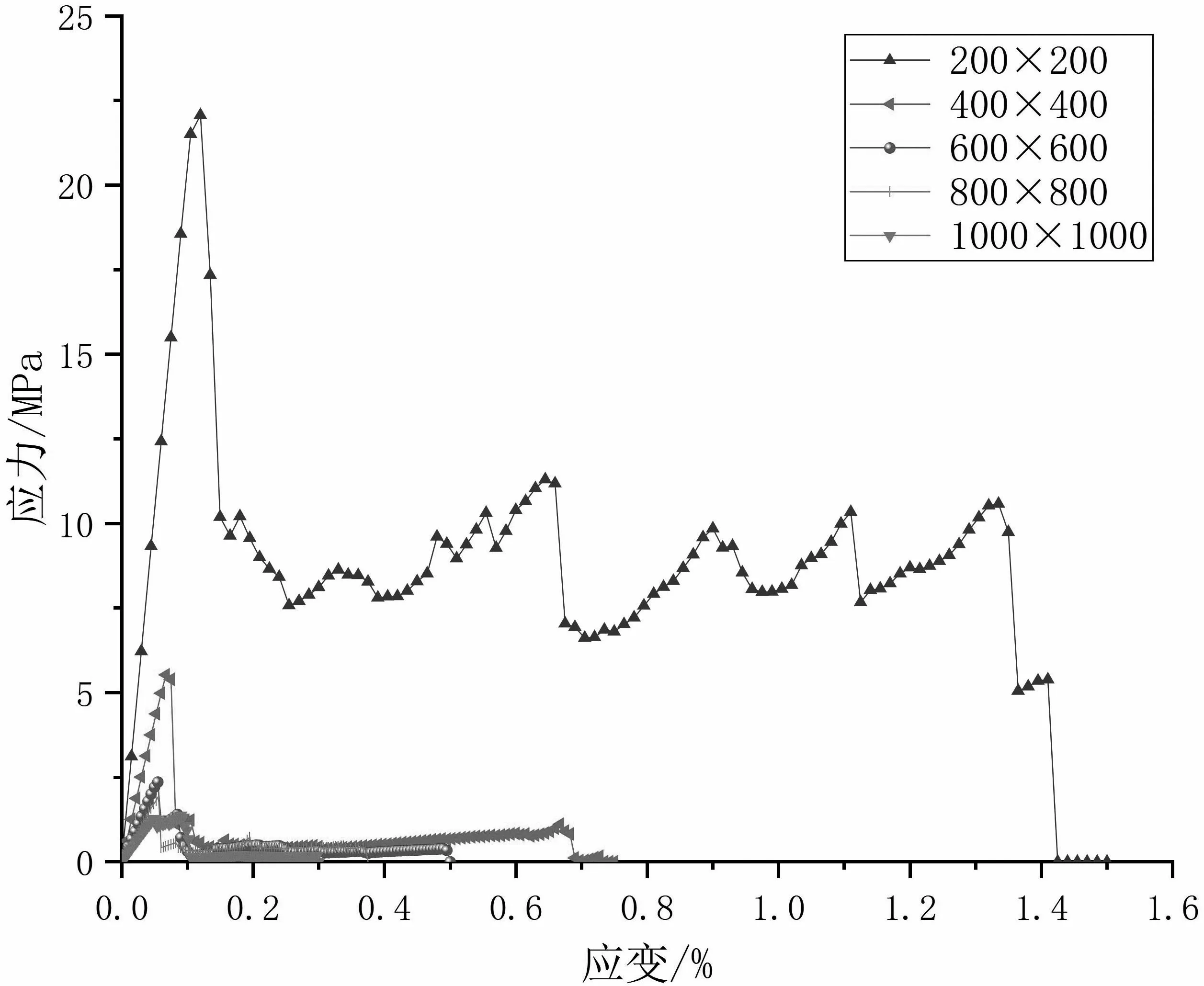
根据试验方案二可得到相同岩桥倾角下不同尺寸模型的应力应变曲线图，图4中a-e的岩桥倾角依次为15 °、30 °、45 °、60 °、75 °，图中尺寸单位都为mm.

由图4-d模型尺寸为200 mm×200 mm、岩桥倾角为60 °的应力-应变曲线可知，随应变的增加，其应力强度先增大后减小. 在应变为0～0.01%时，应力应变呈现正相关关系，应力应变曲线斜率保持不变， 此时， 模型试样处于弹性阶段；当应变在大于0.01%以后，应力骤降，模型试样由微观上的裂纹扩展到宏观上的破坏,模型试样没有塑性阶段.对照图4-d中其余模型尺寸的应力-应变曲线，与尺寸为200 mm×200 mm的应力应变曲线趋势相同，但不同模型尺寸的应力应变曲线斜率不同，所达到的峰值也不同，随模型尺寸增大，应力应变曲线的斜率逐渐减小，峰值强度也随之减小.

a (15 °)

e (75 °)

结合图4中a-e可知，岩石单轴抗压强度随模型试样尺寸的增加而减小.当模型尺寸从200 mm×200 mm变成400 mm×400 mm时，岩石单轴抗压强度下降非常明显；当模型尺寸大于400 mm×400 mm后，岩石单轴抗压强度仍呈现下降的趋势，但相对于小尺寸范围内的变化较为不明显.

将每个角度对应每个尺寸的单轴抗压强度整合后得到表3.

表3 系列尺寸下不同岩桥倾角岩石单轴抗压强度

根据表3可得不同岩桥倾角下岩石单轴抗压强度尺寸效应图.由图5可知，当岩桥倾角为15 °时，岩石单轴抗压强度随尺寸的增大非线性减小，结合图中其余岩桥倾角，岩石的单轴抗压强度与尺寸关系亦存在上述规律，表明含岩桥岩石的单轴抗压强度存在尺寸效应.但不同岩桥倾角下岩石单轴抗压强度随尺寸改变而形成的变化量有所不同.

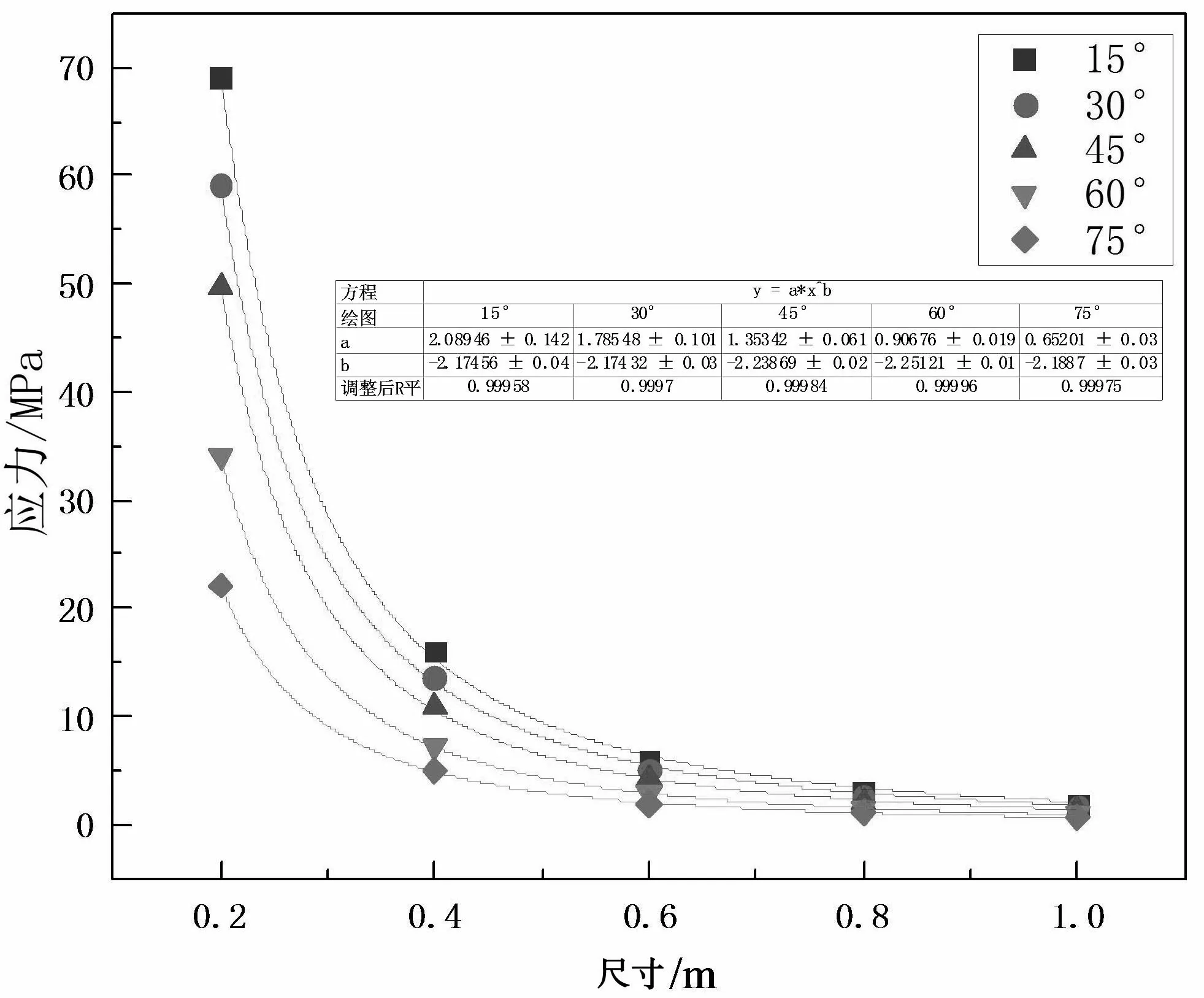
图5 不同岩桥倾角下的单轴抗压强度尺寸效应图

为了研究岩桥倾角对岩石单轴抗压强度尺寸效应的影响，定义Δσ用来描述尺寸效应的明显程度.Δσ值越大尺寸效应就越明显.Δσ的计算公式如式(6)所示.

Δσ=σ200-σ1 000

(3)

式中：σ200代表尺寸为200 mm的岩石单轴抗压强度，σ1 000代表尺寸为1 000 mm的岩石单轴抗压强度.

由表4可知，当岩桥倾角从15 °增大到75 °时，Δσ值在不断减小，表明岩桥倾角的增大，岩石单轴抗压强度的尺寸效应会被弱化.

表4 岩桥倾角与抗压强度的关系

3.2 单轴抗压强度与岩桥倾角和尺寸函数推导

由图5可知，不同岩桥倾角的模型试样在单轴抗压条件下所得到的单轴抗压强度与模型尺寸的函数关系均符合σ=acb，式中σ代表单轴抗压强度；a、b均为系数；c为模型的尺寸.系数a、b的取值如表5所示.

表5 岩桥倾角正弦值所对应的系数a、b

将岩桥倾角的正弦值与系数a、b分别进行拟合，可得到如图6所示的曲线.

图6 系数a与岩桥倾角正弦值关系图

由岩桥倾角正弦值与系数a的拟合曲线可以看到，系数a与岩桥倾角正弦值呈现几近线性的关系.即a=2.72+2.07sinα，式中a为单轴抗压强度与模型尺寸的函数关系中的系数，α为岩桥倾角.

由岩桥倾角正弦值和系数b的拟合曲线图7可以看到，系数b与岩桥倾角正弦值呈现的是非线性的关系，通过拟合得到：

图7 系数b与岩桥倾角正弦值关系图

b=2.79(sinα)3-4.88(sinα)2+2.47sinα-2.54

式中b为应力强度与模型尺寸的函数关系中的系数，α为岩桥倾角.

将系数a与系数b回代到σ=acb中，可得到：σ=(2.72+2.07sinα)c2.79(sinα)3-4.88(sinα)2+2.47sinα-2.54

上式即为单轴抗压强度与岩桥倾角和模型尺寸的函数关系式.

4 结论

本文针对不同岩桥倾角的岩石，进行数值模拟试验，并对其作了尺寸效应分析，得到以下结论：

(1)岩桥倾角会影响岩石的单轴抗压强度.相同模型尺寸下，随岩桥倾角增大，岩石单轴抗压强度下降，当岩桥倾角从15 °变成30 °时，变化较小，当岩桥倾角大于30 °时，岩石单轴抗压强度呈现明显的下降趋势，且下降速度先增大后减小.

(2)在相同的岩桥倾角下，随模型尺寸的增加，岩石单轴抗压强度呈下降趋势，岩石的单轴抗压强度与尺寸呈现的是非线性的负相关关系，存在明显的尺寸效应.

(3)岩桥倾角变化会影响岩石单轴抗压强度的尺寸效应，岩桥倾角增大，尺寸效应会被弱化.

(4)岩石单轴抗压强度与岩桥倾角和模型尺寸的函数关系为：

σ=(2.72+2.07sinα)c2.79(sinα)3-4.88(sinα)2+2.47sinα-2.54