韦氏摆运动机理及关键调控因素的研究

吕欣然，张 萌，马 丽，王 彪

(西南大学 物理科学与技术学院学校，重庆 400715)

近年来，国内学者聚焦于研究基于特定条件下的耦合形式的耦合摆振动[1]，但针对韦氏耦合形式的振转耦合振子的研究仍然较少。而国外对于韦氏摆现有的研究均是基于已有公式推导出的特定条件下的韦氏摆装置所测试的数据，其可推广性有待提高。

1 研究内容与方法

对于韦氏摆运动，其主要是由一个弹簧和一个重物(带侧耳的刚性圆柱)组成的弹簧振子，重物可以在弹簧的作用下作竖直方向的伸缩简谐振动(竖直方向位移为x)，也可以作水平面内的往复扭转运动(水平扭转角度为θ)[2]。

抬升摆锤至平衡位置之上后释放，摆锤将沿弹簧中心线进行上下振荡。经过3～5 s无明显扭动的上下振动后，摆锤在水平面内的扭转幅度逐渐增大，而竖直方向的振动幅度逐渐减小，直至停止上下振动。此时摆锤在水平面内的扭转幅度最大，角度可达180°以上。经过3～5 s的水平扭转运动后，摆锤再次逐渐开始上下振动，如此周期性地重复上下振动与水平往复扭转运动的转换过程。

1.1 理论模型分析

对于韦氏摆运动，其主要是由一个弹簧和一个重物(带侧耳的刚性圆柱)组成的弹簧振子，重物可以在弹簧的作用下作竖直方向的伸缩简谐振动(竖直方向位移为x)，也可以作水平面内的往复扭转运动(水平扭转角度为θ)。

抬升摆锤至平衡位置之上后释放，摆锤将沿弹簧中心线进行上下振荡。经过3～5 s无明显扭动的上下振动后，摆锤在水平面内的扭转幅度逐渐增大，而竖直方向的振动幅度逐渐减小，直至停止上下振动。此时摆锤在水平面内的扭转幅度最大，角度可达180°以上。经过3～5 s的水平扭转运动后，摆锤再次逐渐开始上下振动，如此周期性地重复上下振动与水平往复扭转运动的转换过程。

1.1.1 共振频率条件

当外界周期性驱动力的频率等于弹簧的固有频率时，系统振幅可达最大，此即共振现象。韦氏摆的运动是由竖直和水平两种模态的运动耦合而成，因此存在两个自由度，对于每个模态都其有对应的特征频率解。竖直振动与水平扭转运动都存在各自的固有频率，特征频率由固有频率耦合而成。运动中，摆锤对外表现的合运动频率均可由两种固有频率经不同程度的耦合得到。竖直方向振动的固有频率为ωz，水平方向扭转运动的固有频率为ωθ。两种振动模态互为各自周期性驱动力。因此，当ωz与ωθ趋于相等时，两模态均可趋近振幅最大的共振状态。此时摆锤对外表现的合运动频率亦为特征频率。

1.1.2 弹簧系数条件

为更好地满足韦氏摆共振的频率条件，韦氏摆装置中使用的弹簧也需满足一定条件。下面进行推导。

对与摆锤相比，自身质量与转动惯量可忽略不计的理想弹簧来说，其竖直方向振动固有频率与水平面内扭转角频率分别为

(1)

(2)

式中，m和I分别为重物的质量和转动惯量。其中，弹簧的劲度系数k与扭转系数δ可写作下式：

(3)

(4)

(G：剪切模量，E：杨氏模量，d：弹簧导线直径，D：平均线圈直径，n：绕组数)[3]合并两式可以得到弹簧的线圈直径与弹簧的弹性参数与刚度参数间满足以下关系式：

(5)

由前分析可知，韦氏摆达到共振需要满足

ωz=ωθ

(6)

将式(1)～(5)带入可得弹簧与重物之间需满足的参数关系。这对于挑选重物与弹簧组装韦氏摆装置有一定的指导意义。

1.2 建立动力学模型

对一根柔软弹簧，其劲度系数为k，扭转系数为δ。弹簧下端悬挂一质量为m，转动惯量为I的重锤。以弹簧平衡位置为原点，建立空间柱坐标系，z为纵坐标，θ为水平方向角度坐标。写出系统拉格朗日方程：

(7)

(8)

(9)

若使韦氏摆达到共振情况，需满足

(10)

(11)

(12)

将所求得的特征频率表达式带入式(8)、(9)中，可得韦氏摆竖直方向振动轨迹方程(13)与水平面内扭转振动方程(14)：

(13)

(14)

2 实验验证

2.1 实验准备

实验器材：重锤、不同质量的螺帽、铁皮卷、不同规格的弹簧、游标卡尺、三线摆转动惯量测量仪、高铁架台。

实验中所采用的重锤上的螺杆可以通过组装质量不同的螺帽或铁皮卷进行配重，也通过改变配重在螺杆上的距离改变转动惯量。

为了更好地用tracker进行追踪，在螺杆上粘贴轻质红色标记，以利于水平扭转追踪；在重锤底部粘贴白色细条标记，以利于竖直振动追踪。

2.2 运动模态的周期性转化行为

同等条件下，在铁架台底部和正对铁架台处安置拍摄装置同时进行拍摄，保证拍摄平面与物体运动平面平行。实验中利用tracker在竖直振动模式和水平扭转模式下追踪示意图如图1所示。

图1 Tracker追踪图

将同一条件下两种模式的tracker追踪所得Z-t图与θ-t图进行拟合，拟合结果如图2所示。

图2 竖直方向与水平方向轨迹追踪图

需要注意的是，此图中因两者的纵坐标不同，无法定量比较，因此只需关注两者横坐标的关系。可以发现，韦氏摆运动过程中其竖直振动与水平扭转运动确实存在周期上的相互转化。当竖直振动达到最弱时，水平扭转运动也相应达到最强；而随着水平扭转运动的减弱，竖直振动也对应增强。

2.3 理论模型验证

将tracker追踪得到的竖直运动数据导入matlab进行傅里叶频谱分析，得到结果如图3所示。根据理论分析可知，图中两个尖峰值处所对应的横坐标即为韦氏摆运动的两个特征频率F1和F2，从而得到特征角频率ω1、ω2。

图3 傅里叶频谱分析图

根据建立的韦氏摆竖直振动理论轨迹公式，将初始条件和特征角频率带入，通过matlab绘制函数(图4)，与实际振动曲线(图5)进行同等标度拟合，拟合结果如图6所示，在误差范围内以及理论建模时不考虑能量耗散的前提下，发现在拍频、平均角频率、耦合振幅上拟合效果良好。

图4 Matlab绘制理论运动轨迹

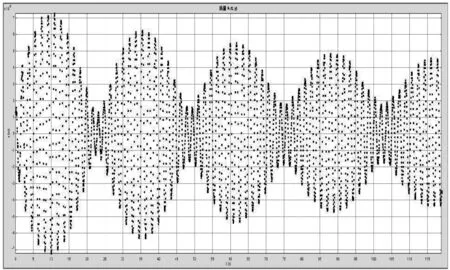
图5 实际运动轨迹

图6 实验运动轨迹与理论运动方程等标度拟合

2.4 不同参数对运动的影响

证明韦氏摆运动存在水平和竖直两种模式间的周期性转化现象后，采用控制变量法探究不同参数对韦氏摆运动的影响。

2.4.1 初始条件z0

初始条件z0对运动的影响。在其他条件相同时，黄色轨迹在距离平衡点18 cm处释放，蓝色轨迹在20 cm处释放，将两者进行进行同等标度拟合，得到图7。分析其运动轨迹，发现两者的波包最大振幅与z0成正比，拍频、平均频率和耦合振幅几乎不变。

图7 不同z0情况下的轨迹对比图

2.4.2 初始条件θ0

初始条件θ0对运动的影响。在其他条件相同时，蓝色轨迹在距离平衡位置2π处释放，红色轨迹在距离平衡位置4π处释放，将两者进行进行同等标度拟合，得到图8。分析其运动轨迹，发现两者的波包最大振幅与θ0成正比，拍频、平均频率和耦合振幅几乎不变。因此，初始条件z0和θ0主要影响表征分运动强度的波包最大振幅，对表征运动转化的耦合振幅影响不大。

图8 不同θ0情况下轨迹对比

2.4.3 转动惯量I

在其他条件相同时，如图9所示，三条轨迹中摆锤的转动惯量分别为1.65 gm2,1.55 gm2和1.48 gm2。分析其运动轨迹，发现其与初始条件Z0和θ0对运动影响不同的是，转动惯量I的改变不仅影响运动的波包最大振幅，还会影响竖直振动和水平转动的耦合情况。

图9 不同转动惯量I下运动轨迹对比

根据理论模型，系统要实现运动完全转化的韦氏摆现象，竖直振动和水平转动的固有频率需满足相等关系，即(6)式。求解该等式，可以得到实验中实现韦氏摆共振现象所需满足的摆锤理论转动惯量，为1.5 gm2。三种情况中，紫色轨迹摆锤转动惯量最接近理论值，因此，其耦合振幅最小，运动在两种模式间的转化也更彻底。

同时可以发现，随着实验转动惯量值与理论值的差值增大，其运动轨迹的包络现象越发不明显，有趋于简谐振动的趋势。这也说明了韦氏摆是弹簧振子结构中的一种特殊情况，当韦氏摆结构中的摆锤满足特定条件时，才会有韦氏摆共振现象出现。

3 结 语

通过实验验证了韦氏摆动力学模型，研究了不同参数对韦氏摆运动的影响，但仍存在一定不足：模型构建未充分考量空气阻力、连接处摩擦在内的衰减系数，无法定量计算对于振动的衰减及衰减程度；这也是未来实验将改进的一个方向。

近年教育改革政策的出台，国家不断加大对教育方面的投入，高校规模呈现了扩容之势。随着教育质量的不断提高，教育资金投入的不断增大，各大高校的实验内容也会增加。韦氏耦合运动有望成为大学物理实验中重要项目。韦氏摆运动研究对于大众科普和中小学教育同样具有重要意义。利用该装置，科普工作者可以进行耦合运动与能量守恒转化现象的科学普及。