基于局部特征的自然场景配准算法比较分析
赵思雨,刘岩松,柳倩
(沈阳航空航天大学,辽宁 沈阳 110136)
0 引 言
作为图像识别领域的研究热点之一,图像配准在医学影像处理、遥感数据分析、计算机视觉及三维建模等领域应用十分广泛[1]。基于特征的配准算法是众多配准算法中效率最高且效果最好的一种,其中SIFT、SURF 和ORB 三种算法使用最多、应用最广。2004年Lowe[2]提出SIFT 算法并在IJCV 上发表。该算法的独特性在于将兴趣点用直方图进行描述,并在亮度上进行归一化,所以在尺度变换和光照变换下性能突出。2006年在SIFT 的基础上,Bay[3]等人提出了鲁棒性更强、效率更高的SURF 算法。该算法利用盒子滤波器和快速积分来提高特征检测速度,并且在匹配上与SIFT有着相近的效果。但是由于SIFT 和SURF 特征提取的复杂性,2012年Rublee[4]等人基于ROSTEN[5]和Canlonder[6]描述子提出了ORB 算法。该算法完善了FAST 尺度变换不变性的和BRIEF 噪声影响不变性,虽然在性能上逊色于SIFT和SURF,但是提高了检测速度。每个算法都有自己独特的性能,选择合适的算法将一定程度上提高其应用效果,故特征配准算法的研究是重要且必要的。
近年来有关上述三种配准算法的比较研究也很多,刘伟[7]等发现在SIFT、SURF 和ORB 三种算法中,ORB 特征点的检测速度最快,SIFT 匹配对数最多,SURF 性能适中,更适用于特征提取与匹配。索春宝[8]等通过不同变换对比实验得出:相比于SIFT 和SURF 算法,ORB 在速度上更有优势,但SURF 表现出的鲁棒性更加全面。徐妍[9]等通过研究SIFT 和SURF 两种算法的配准速度与精度,发现SIFT 算法的精度更高,SURF 算法的速度更快。林志东[10]等在光照差异和视角变换条件下对SIFT 算法与SURF 算法进行对比实验发现:SIFT 特征点提取数量更多,且适用于具有光照差异的图像。SURF 运行速度更快,在视角差异的图像中匹配效果更佳。陈敏[11]等通过旋转不变性实验对SIFT 算法与SURF 算法进行比较,发现SIFT 在旋转条件下匹配性能更优,而SURF 精度虽低,但速度更快。以上是学者们对三种算法的运行速度、配准精度和鲁棒性等方面进行的研究,但是缺少系统性的对比,尤其是影响算法鲁棒性的因素考虑的还不够全面。
因此,本文对SIFT、SURF 和ORB 三种特征配准算法进行特征提取与匹配实验,从算法用时和匹配数目两个方面对算法的性能进行比较,分析三种算法在自然场景下的实时性及鲁棒性。
1 特征配准算法原理
1.1 SIFT 算法
SIFT 是一种具有尺度不变性和旋转不变性的图像局部特征描述子[10],是在不同的尺度空间中,通过寻找极值点的精确位置和主要方向,构建特征点描述符来提取特征。算法主要包括以下4 个步骤。
1.1.1 尺度空间极值检测
通过利用不同尺度的高斯卷积核与图像进行卷积运算,并对上下相邻尺度的图像进行差分,得到高斯差分(Derivative of Gaussian,DOG)尺度空间:
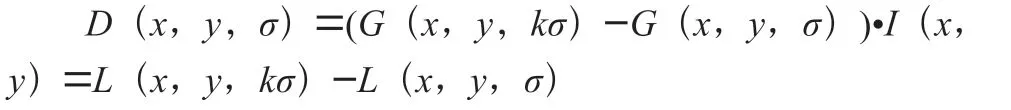
利用非极大值抑制的策略,判断像素点是否为邻域26点的DOG 最大值或最小值,从而得到一定范围内离散空间上的极值点。
1.1.2 特征点定位
极值点并非都为特征点,通过采用曲面拟合的方法,利用插值来寻找特征点,以实现对于低对比度点的过滤。通过使用高斯差分对边缘特征点进行滤波,实现对极值点的二次过滤。
1.1.3 特征点方向赋值
计算特征点附近像素的梯度方向和梯度赋值:
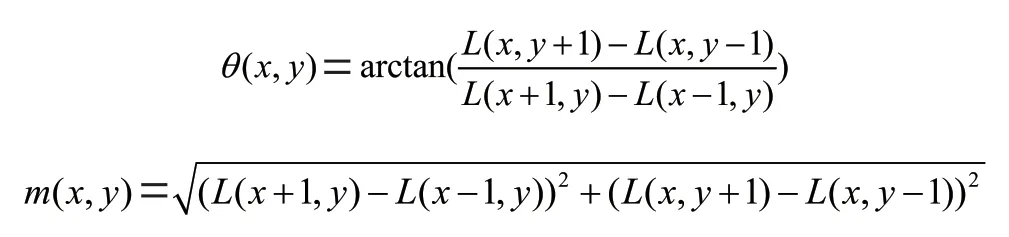
使用基于直方图统计的方法,得到邻域内所有像素的梯度和它们的方向。其中直方图的最大值方向代表了特征点的主方向。
1.1.4 特征点描述
对特征点周围取8×8 的区域,并将每个区域划分成4×4 的小区域,且每个区域有8 个梯度方向,对区域内的像素点的梯度方向进行统计,最终可以得到关于特征点的4×4×8 的128 维描述符,并做归一化处理。如图1所示为128 维描述符。
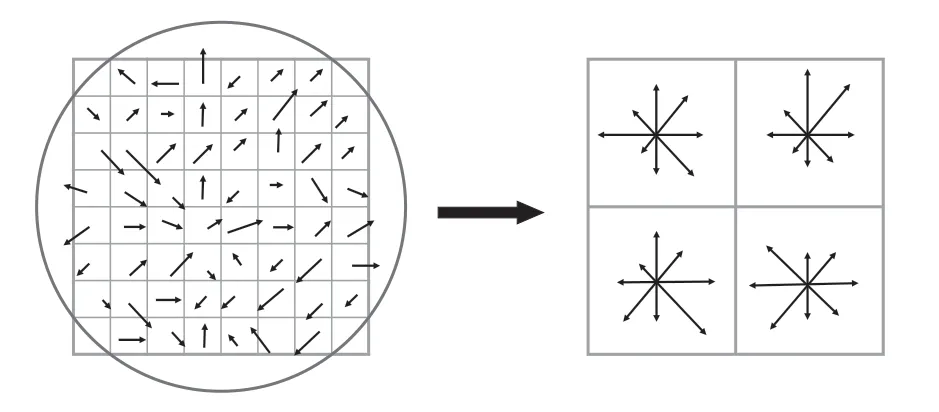
图1 SIFT 特征点描述符
1.2 SURF 算法
相比于SIFT 算法,SURF 算法在尺度空间构造和特征点描述方面进行了优化改进[11]。SURF 算法步骤与SIFT 算法大致相同,但在存在一些差异:
(1)在构建尺度空间时,SIFT 使用高斯函数卷积来构造尺度空间,但是SURF 使用盒子滤波器,即不需要重复采样,并且在卷积过程中使用了积分图像的概念,可以加速特征的提取。
(2)在极值检测时,SURF 比SIFT 多采用Hessian 矩阵处理每个像素点,然后再用非极大值抑制的策略检测初步极值点。其中Hessian 矩阵为:
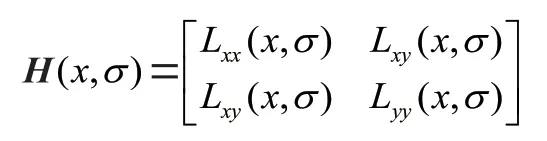
(3)在特征点方向赋值时,与SIFT 不同,SURF 是通过统计特征点圆形邻域内的Haar 小波特征来确定主方向。
(4)在特征点描述时,SURF 选取一个正方形窗口,将正方形划分为16 个5×5 的子区域,每个子区域有4 个值,因此构成16×4 的64 维向量,是SIFT 的一半,可以大大节省运算量。如图2所示为64 维描述符。
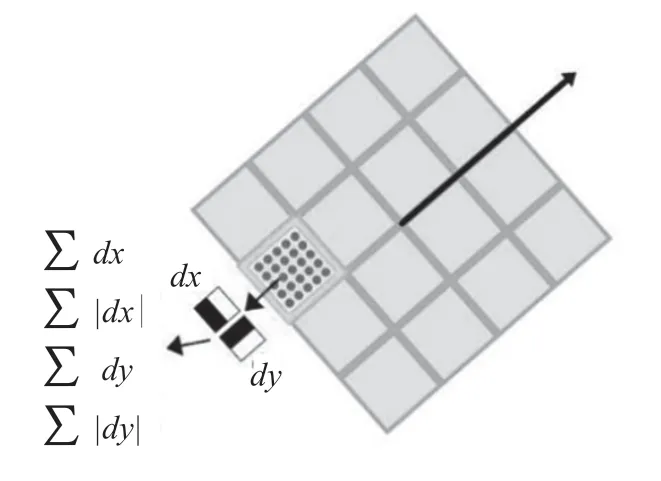
图2 SURF 特征点描述符
1.3 ORB 算法
ORB 算法是一种基于FAST 特征检测[12]以及BRIEF 特征描述[13]的一种局部不变特征算法。算法主要包括以下两个步骤。
1.3.1 FAST 特征检测
使用决策树将像素点p与其半径为3 的圆邻域的16 个点的灰度值进行比较,从而初步筛选出极值点。再用Harris算法对极值点进一步筛选,得到优质的特征点。
ORB 算法采用灰度质心法对具有旋转不变性的特征点进行方向赋值。将特征点邻域像素的矩定义为:
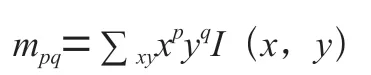
则矩的质心为:

因此可以定义特征点的方向θ为:
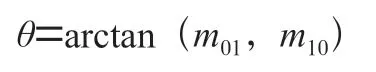
1.3.2 BRIEF 特征描述
ORB 算法是基于BRIEF 进行特征描述,但由于BRIEF特征描述不具备旋转不变性,所以需要根据特征点自身的旋转来调整描述符方向,以实现BRIEF 的旋转不变性。
2 实验结果分析
2.1 实验数据及平台
为比较SIFT、SURF 和ORB 三种特征配准算法在自然场景下的实时性和鲁棒性,本文对三种算法进行了特征提取与匹配实验。实验数据来源于智能手机iPhone13pro 实拍的室外图像,其中摄像头焦距为26 mm、光通量为1.5,拍摄出的图像分辨率为12 PM、大小为4 032×3 024。利用Adobe Photoshop 2021 和Python 3.7 实现图像的各种变换,如图3所示。实验平台为Intel Core M i7-10750H,CPU 为2.60 GHz,64 位系统,运行内存16 GB,在Python 3.7 下进行编程。
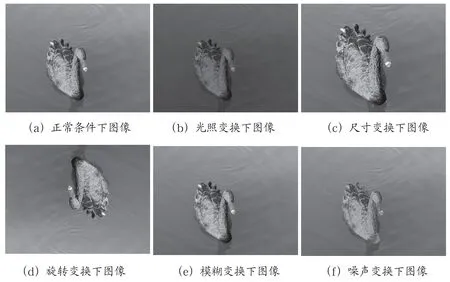
图3 不同条件下的实验数据
2.2 特征点提取与匹配实时性分析
对实验数据分别采用SIFT、SURF 和ORB 三种算法进行特征点的提取与匹配实验。使用OpenCV 提供的特征提取算法的调用接口,设置三种算法的提取点数均为500,选择快速最近邻(FLANN)算法[14]进行特征匹配,将其阈值设置0.5,然后通过随机取样一致性(RANSAC)算法[15]剔除图像误匹配对。通过比较运行时间,进一步反应对应算法的特征提取与匹配速度。
图4和图5分别为三种算法在自然场景中特征点提取和匹配后的图像,在特征分布上,ORB 过于集中,SIFT 和SURF 分布较广且均匀。在匹配数目上,SIFT 和SURF 匹配特征数目较多,ORB 匹配特征数目较少。

图4 三种算法提取特征点后图像
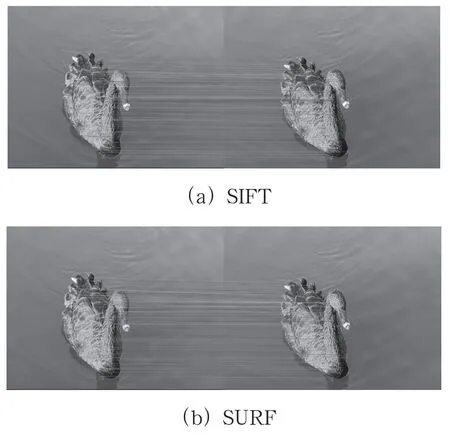
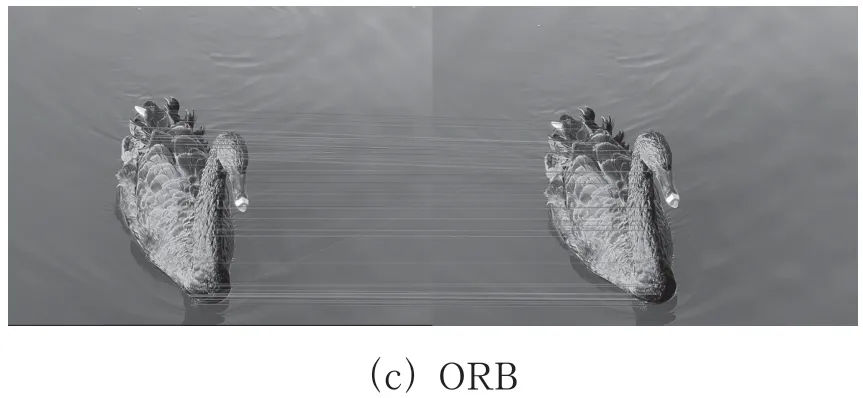
图5 三种算法特征匹配后图像
不同算法的运行时间和匹配数目如表1所示。在结果中可以看出,在提取同等数量特征点时,三种算法提取特征点的时间关系是SIFT >SURF >ORB。其中ORB 算法的提取时间要远远小于SIRF 和SURF 的时间,SIRF 和SURF 用时接近。在相同的匹配环境下,从各算法的匹配用时与匹配数目相结合进行比较,ORB 的匹配速度最具优势,其次是SURF,最后是SIFT。整体上,ORB特征配准算法更具实时性。
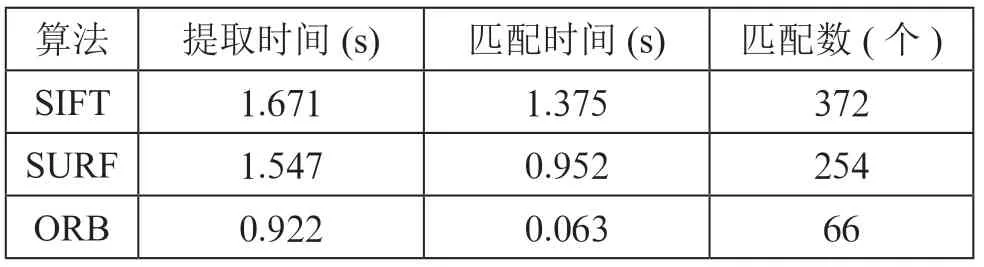
表1 特征提取与匹配实验结果
2.3 光照变换鲁棒性分析
在自然场景下,光照变化普遍发生。由于天气变化、相机曝光不同或者拍摄角度差异等不可控因素的影响,会导致同一场景在不同图像上光照条件不一致。不同的光照条件会增大图像之间的成像差异,这使得光照变换下的图像匹配成为一个普遍而具有挑战性的问题。为研究光照变换对三种算法性能的影响,本文利用计算机处理技术将图像亮度值变化量设置为-100%~100%,步长为25%,生成不同光照条件下的场景图像b1~b8,将处理后的图像与原始图像a0进行匹配,算法处理效果分析如下。
结合表2和图6可以得出:总体上光照条件的变化对三种算法均有影响,SIFT 受到光照变换的影响最小,其次是ORB,SURF 受到影响最大。SURF 在光照变化量不大时,表现出不错的稳定性。但随着亮度变化量继续增大,特征匹配对数也都随之急剧下降,降低到一定程度时,SURF 无法进行特征匹配。SIFT 和ORB 在亮度值减小的图像上特征匹配对数较为平稳,且远远多于亮度值增大的图像。

表2 各算法匹配光照变换图像的匹配对数
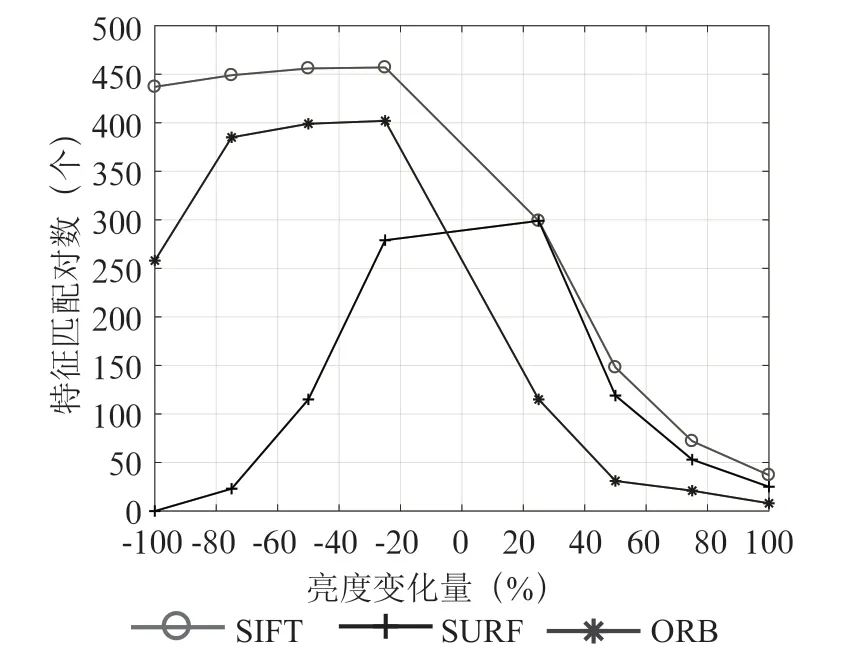
图6 光照变换下匹配对数折线图
2.4 几何变换鲁棒性分析
尺度变换、旋转变换等几何变换在自然场景图像中十分普遍,相机的稳定性、拍摄距离及拍摄角度都会使图像在几何形态上发生改变。在尺度变换中,尺度的变化不仅会改变图像中特征点的尺度信息,还会产生新的特征点。当图像发生旋转时,各像素点会随图像旋转相应的角度,像素点的梯度幅值和特征点的方向信息会随之改变。几何变换改变了特征点的信息,增加了特征提取的难度,对后续图像匹配工作造成挑战。为探讨三种算法在几何变换下的鲁棒性,本文利用计算机处理技术生成尺度变换和旋转变换等条件下的场景图像:将图像缩放系数从0.25 变化至0.85,步长0.15,得到尺寸变换图像c1~c5;将图像顺时针旋转18°~90°,步长18°,得到d1~d5的旋转图像。将几何变换变换后的图像与原始图像进行匹配,算法处理效果分析如下。
结合表3和图7可以发现,当尺寸变化不大时,三种算法有足够的特征匹配数。当尺寸变换比较大时,三种算法特征匹配数目均减少,SURF 和ORB 迅速下降,SIFT 下降速度较缓,表现出较好的鲁棒性。

表3 各算法匹配尺寸变换图像的匹配对数
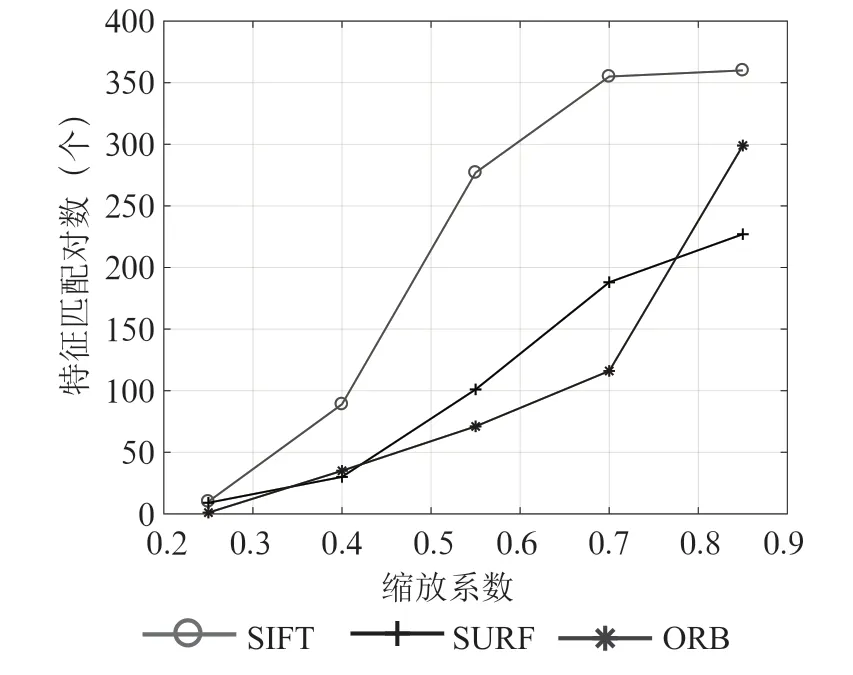
图7 尺寸变换下匹配对数折线图
根据表4和图8可以得出,当图像发生旋转时,特征匹配对数会减少,但三种算法都能获得一定量的特征匹配。SIFT 和ORB 均表现出良好的稳定性,且SIFT 算法在匹配数目上更胜一筹。总体上,SIFT 算法在几何变换下鲁棒性优于其他两种算法。
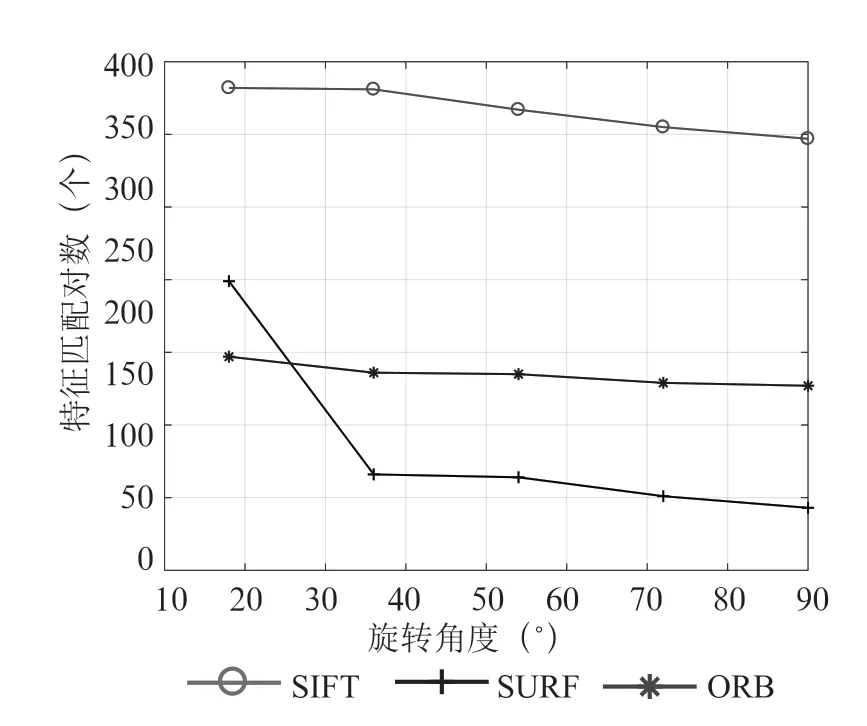
图8 旋转变换下匹配对数折线图

表4 各算法匹配旋转变换图像的匹配对数
2.5 模糊变换鲁棒性分析
由于成像系统散焦、相对运动及拍摄抖动等原因,图像易发生模糊、不清晰现象。这种现象会导致图像的分辨率和识别能力下降,对图像匹配造成一定程度上的挑战。为研究三种算法在模糊变换下的鲁棒性,本文利用计算机处理技术对图像进行高斯模糊处理,半径由1 变化至5,生成模糊场景图像e1~e5,将处理后的图像与原始图像逐一匹配,算法处理效果分析如下。
通过表5和图9可以得出,在较小的高斯模糊半径范围内,三种算法都能获得一定量的匹配数,但随着模糊半径继续增大,三种算法的匹配对数均明显下降。当模糊程度较大时,三种算法趋于一致,鲁棒性都比较差。
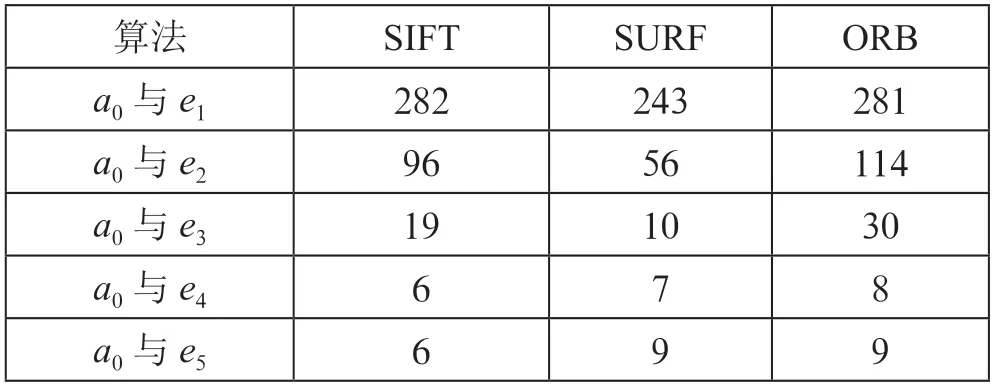
表5 各算法匹配模糊变换图像的匹配对数
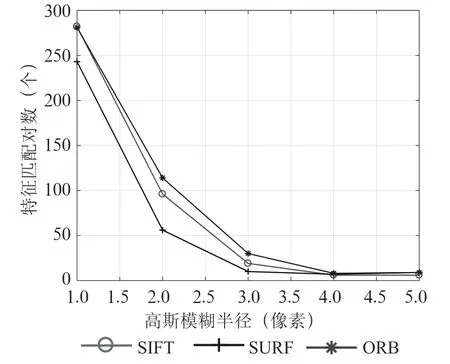
图9 模糊变换下匹配对数折线图
2.6 噪声鲁棒性分析
在获取图像的过程中,外部环境和电子系统自身都会不可避免地产生噪声。噪声会导致图像中像素点随机的出现灰度值的突变,影响图像特征点位置的检测,为特征匹配工作增加难度。为探讨噪声变化对三种算法的性能影响,本文利用计算机处理技术对图像添加高斯噪声,半径由5 变化至25,步长为5,生成噪声变换条件下的场景图像f1~f5,得到的图像与原始图像依次匹配,算法处理效果分析如下。
结合表6和图10可以看出,当加入噪声后,三种算法特征匹配对数随着噪声的强度增大而减少,当噪声强度比较大时,三种算法匹配结果趋于稳定。整体上,SURF 算法的鲁棒性更强。
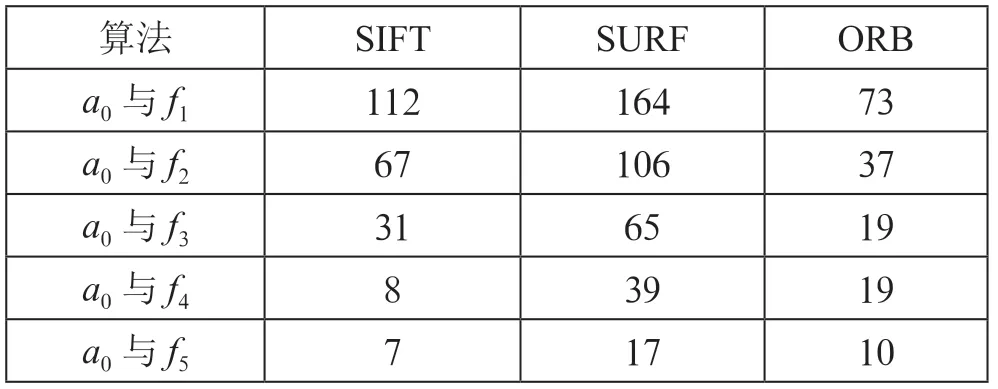
表6 各算法匹配噪声变换图像的匹配对数
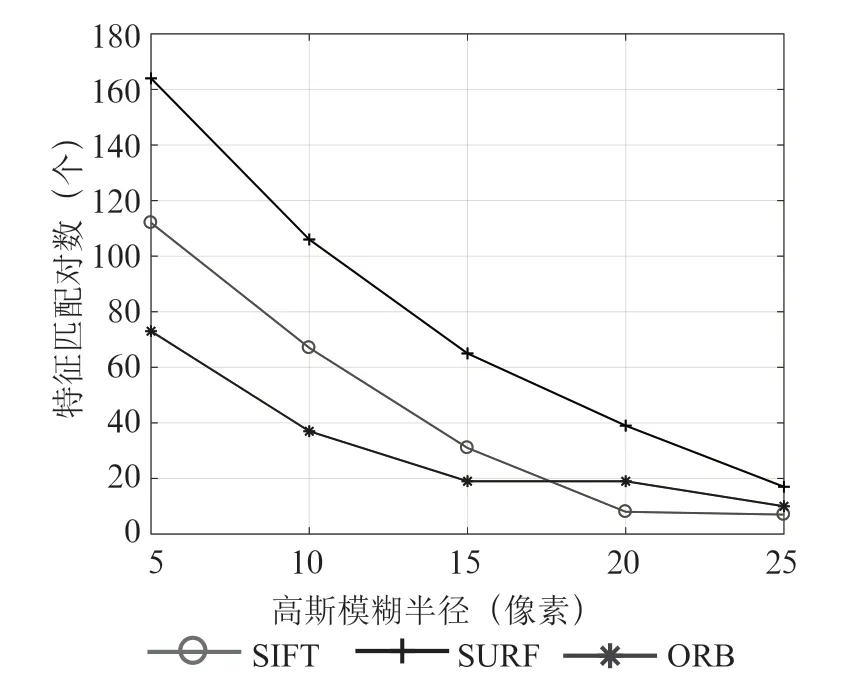
图10 噪声变换下匹配对数折线图
3 结 论
本文选取SIFT、SURF 和ORB 三种主流算法,通过原理分析和仿真实验,比较各算法在图像特征提取与匹配中发生图像变换时的表现,探究出各种算法的实时性和鲁棒性,得出以下结论:
(1)SIFT 算法特征稳定、分布广泛,匹配数目多,但是速度慢,且描述子过大,对平台要求高。在光照变换和几何变换条件下仍能获取较多的匹配对数,鲁棒性较强。在面向光度变化或尺度变化的图像时,可以优先选择SIFT 算法。
(2)SURF 算法特征匹配数目仅次于SIFT 算法,但匹配速度和特征分布状态优于SIFT 算法,噪声变换下的鲁棒性明显优于其他两种算法,在处理受到噪声干扰的图像较为占优。
(3)在实时性方面,ORB 算法具有很大优势,在模糊变换下获取的匹配对数较多,但特征点分布效果差,匹配数目少。所以在图像分辨率低或特征点多的情况下,可以优先考虑ORB 算法。
本文结果可以为图像特征研究工作提供参考,除了上面介绍的经典特征匹配算法,还有许多表现效果很好的算法值得研究,接下来考虑如何设计更全面的评价机制,进一步对图像特征相关算法进行比较。

