一种新四维超混沌系统的分岔分析及应用

王春娥，崔 岩，赵少卿，周六圆，王申鹏

(上海工程技术大学 机械与汽车工程学院，上海 201620)

0 引言

1963年，洛伦茨(Lorenz)在研究气象中存在的湍流现象时，根据当时可依据的非线性理论构建出了一个三维非线性微分方程组，即Lorenz系统[1]。此后，若干非线性系统及同步和控制方法的不断涌现[2-7]，使混沌学迅速发展并逐步走向成熟[8]。分岔是非线性系统所具备的独特现象[9]，混沌系统平衡点稳定性发生改变将会引起系统的局部分岔，系统局部动力学行为也会随之发生变化。Hopf分岔是系统局部分岔中非常基本而又至关重要的一种。文献[9]研究了四维混沌的Hopf分岔行为，并进一步发现了一种通向混沌的路径。文献[10]在非线性动力系统的基础上，丰富了Hopf分岔理论。文献[11]对一个四维超混沌系统进行了Hopf分岔反控制研究。文献[12]研究了时滞Lü系统的Hopf分岔，得到Hopf分岔产生的条件。文献[13]研究了时滞扰动类Chen系统Hopf分岔及控制，针对某一输入量受扰动设计出一种控制其分岔临界点的新方法。文献[14]研究了时滞Rössler系统的Hopf分岔，验证了时滞参量在时滞分岔点附近的改变会影响系统的稳定性。文献[15]对一个新超混沌系统的控制问题进行研究，设计了一种自适应滑模变结构控制，验证了该控制对外界扰动具有鲁棒性。文献[16]研究了三八超混沌系统的时滞反馈控制，分析了时滞值对平衡点的影响，给出了在该点附近Hopf分岔的参数和时滞条件。文献[17]研究了一类具时滞超混沌系统的稳定性及控制的问题，将混沌系统控制成为稳定状态。超混沌系统因其复杂度更高，其状态轨迹和系统产生的混沌信号会更加复杂[18]，在图像加密、金融系统等领域有很高的应用价值。文献[19]研究了一类分数阶金融模型的混沌控制问题，运用时滞反馈控制法成功控制了金融模型的混沌行为。文献[20]通过改进图像变换形式与分块方法，验证了图像加密算法具有更强的鲁棒性和安全可靠性，可以充分抵御各种针对性攻击。文献[21]构建了一个新型的四维混沌系统，利用混沌和密码学的对应关系将其应用到图像加密领域，验证了新系统具有很好的混沌特性，但缺少对新系统的分岔分析及线性控制。

本文构建了一个新四维超混沌系统，w为新引入的状态变量。分析新系统的混沌特性及稳定性，结合Hopf分岔理论判断分岔类型及方向。在新系统中加入线性控制器，验证时滞Hopf分岔点是否发生延迟，并将新系统应用在图像加密方面，分析其加密效果及安全性能。

1 系统分析

本文所研究的四维超混沌系统描述为：

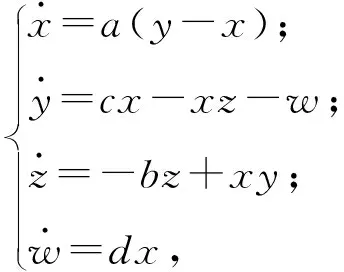
(1)

其中：x,y,z,w为系统(1)的状态变量；a,b,c,d为系统(1)的参数，且该系统存在唯一一个平衡点E0=(0,0,0,0)。当参数取a=35,b=3,c=33,d=8时，系统(1)存在一个典型的超混沌吸引子，混沌吸引子相图如图1所示。

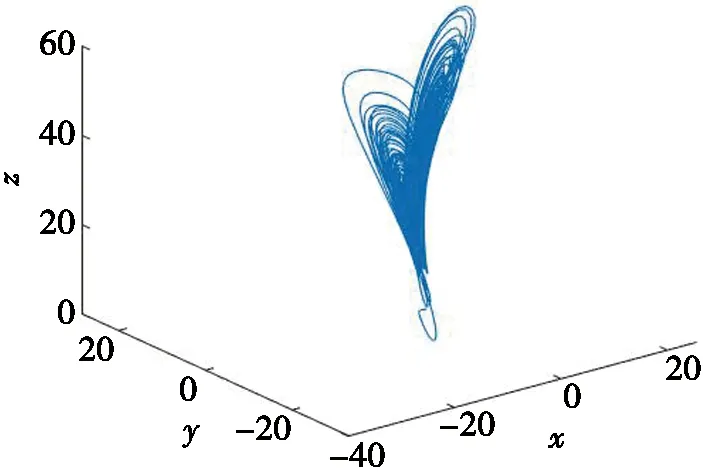
(a) x-y-z三维投影相图

1.1 混沌特性分析

利用LE工具箱计算新系统(1)的李雅普诺夫(Lyapunov)指数，得到4个李雅普诺夫指数LE1=0.343,LE2=0.052 2,LE3=-0.305,LE4=-36.640，其中有两个李雅普诺夫指数大于零，即系统(1)为超混沌系统。

1.2 稳定性分析

在超混沌系统(1)的第2个非线性方程中添加时滞项τ，时滞系统方程描述为：

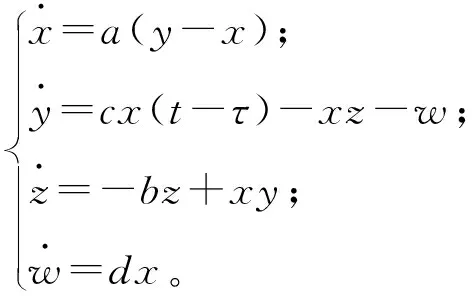
(2)

当时滞项τ=0时，系统(1)在平衡点E0=(0，0，0，0)是局部渐近稳定的，雅可比(Jacobi)矩阵为：

特征方程如下：

(λ+b)(λ3+aλ2-acλe-λτ+ad)=0。

(3)

根据换元法令P1=a,P2=-ac,P3=ad，若仅考虑虚根，当τ=0时，系统(2)的特征方程为：

λ3+P1λ2+P2λ+P3=0。

(4)

根据劳斯-赫尔维茨(Routh-Hurwitz)判据可知，若满足条件P1>0,P2>0,P3>0,P1P2-P3>0，则方程(3)的特征根实部均为负值。将对应参数代入上述不等式可知，时滞系统(2)在平衡点E0=(0,0,0,0)处是局部渐近稳定的。

1.3 Hopf分岔分析

当时滞参数τ>0时，λ=±iω是特征方程的一对纯虚根，令λ=iω并代入方程(3)中有：

-iω3-P1ω2+P2iω(cosωτ-isinωτ)+P3=0。

令实数和虚数分别等于零得：

(5)

移项，平方相加得：

(6)

假设方程(6)至少有一实根，令ξ=ω2则有：

(7)

令：

(8)

则有：

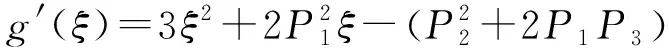
假设ω=ω0为式(5)的一个实根，代入式(5)得：

(9)

再将ω=ω0代入式(9)可得时滞参数τ：

(10)

由式(10)可知：(ω0,τn)为式(3)的解，即λ=±iω0是式(3)的一对纯虚根，时滞参数τ=τn为系统(2)的最小时滞参数。下面针对系统(2)在平衡点E0=(0,0,0,0)时，给出分岔条件。假设方程的特征根为λ(τ)=α(τ)+iω(τ)，则λ=±iω0是特征方程(4)的一对共轭的纯虚根，使得α(τn)=0,ω(τn)=0。

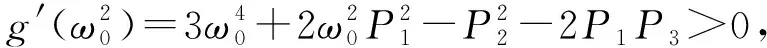
证明对于式(3)两边求导得：

(11)

由式(5)可得：

λ3+P1λ2+P3=P2λe-λτ。

(12)

(13)

则有：

(14)

当时滞参数τ=τn时，方程(2)存在特征根iω0，代入式(4)得：

(15)

根据欧拉公式e-iω0τ=(cosω0τ-isinω0τ)，|e-iω0τ|=1，式(15)两边取绝对值得：

(16)

即：

(17)

根据式(14)和式(17)可得：

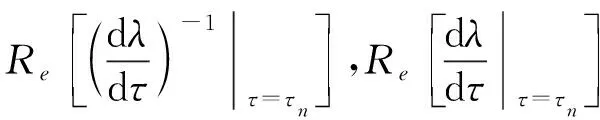
根据上述计算分析与Hopf分岔理论[9]可得下面结论：

(Ⅰ)当τ∈[0,τ0)时，时滞系统(2)在平衡点E0处是趋向稳定的。

(Ⅱ)当τ=τn,(n=0,1,2,3,…)时，时滞系统(2)在平衡点E0处发生Hopf分岔并产生极限环。

(Ⅲ)当τ>τ0时，时滞系统(2)在平衡点E0趋向不稳定，但在一定范围内存在较为稳定的极限环。

综上，系统发生的为超临界Hopf分岔。

在工程实际应用中，可以通过添加控制器延迟Hopf分岔的发生。设计线性控制器为u=k(y-p)，其中，p为平衡点E0处y点的坐标，即p=0。将线性控制器添加到时滞系统(2)的第2项中，对时滞分岔点进行延迟控制，用MATLAB 软件进行仿真验证。计算出受控系统的时滞参数τ为：

2 数值仿真

2.1 数值分析

为了方便计算超混沌系统的时滞参数，取a=8,b=2,c=-1.17,d=1，系统(2)转化为：

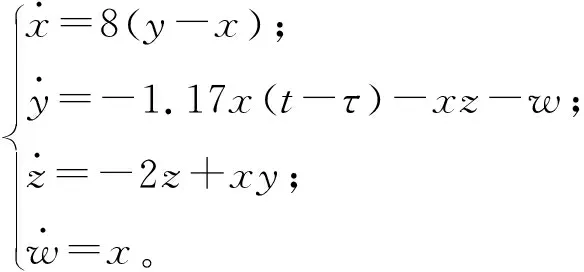
(18)

根据方程(5)可取ω0=0.601 5,将ω0代入到方程(10)中，得第一个大于零的时滞τ0=0.673 9。根据上述分析中的结论可得如下推论：

(Ⅰ)当τ∈[0,0.673 9)时，系统(18)在平衡点E0=(0,0,0,0)处短时间内趋近稳定状态。

(Ⅱ)当τ≥0.673 9+2.967 8nπ时，系统(18)在平衡点E0=(0,0,0,0)发生超临界Hopf分岔且产生稳定的极限环。

系统加入线性控制器后，经Routh-Hurwitz判据得k<1.061 9，本文取k=0.7，得ω0=0.666 1，可计算得出时滞分岔临界值为τ=0.722 9，绘出受控系统的时滞分岔图。

2.2 仿真结果

运用MATLAB软件仿真得出不同时滞参数下该系统的时滞相图与时间序列图。

(a)时滞参数τ∈[0,0.673 9)时，取τ=0.663 9。

当τ=0.663 9时，系统(18)的相图如图2所示。由图2可知：系统从初值迭代后逐渐趋向于平衡点E0，此时未形成极限环，如图2a。图2b中状态变量x,y,z,ω在较短时间内趋近平衡点。由此推论(1)得证。

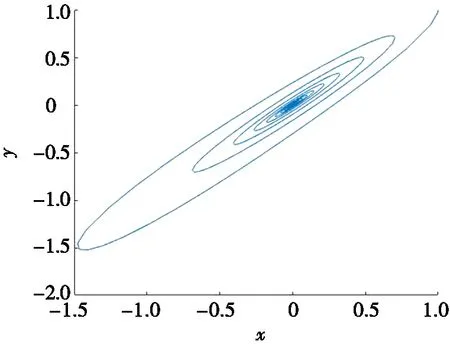
(a) x-y平面投影相图

(b)时滞参数τ≥0.673 9+2.967 8nπ,(n=0,1,2,3,…)时，取τ=0.673 9和τ=0.683 9。

当τ=0.673 9时，系统(18)的相图如图3所示。观察图3a可知：系统的初值迭代后不趋向于平衡点E0，表明系统开始形成极限环。图3b可以观察到状态变量x,y,z,ω在经历了30个时间积分后趋于稳定振荡，即开始形成极限环。

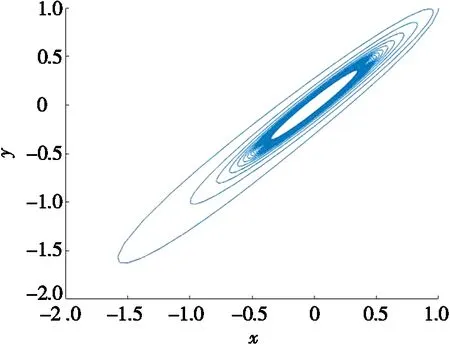
(a) x-y平面投影相图

当τ=0.683 9时，系统(18)的相图如图4所示。图4a表明系统已经形成清晰的极限环。图4b中状态变量x,y,z,ω在经历5个时间积分后，振荡趋于稳定即产生了极限环，此时发生Hopf分岔。由此推论(2)得证。

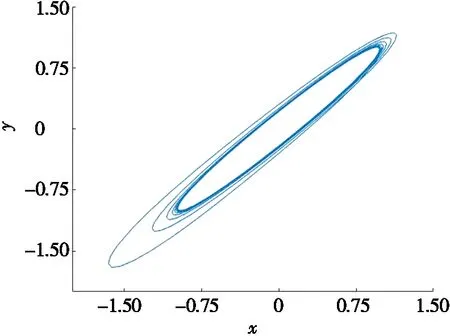
(a) x-y平面投影相图

图5为时滞超混沌系统的局部分岔图，显然τ=0.673 9是分岔临界点，进一步验证推论的正确性。当τ<0.673 9时，系统为渐近稳定状态，趋向于平衡点E0；当τ>0.673 9时，发生超临界Hopf分岔，产生稳定的极限环。由图5可以看出：受控系统与原系统相比，时滞分岔点由0.673 9延迟到0.722 9，延迟了由时间扰动引起Hopf分岔的发生；振动幅值也稍有降低，说明加入控制器后迭代更加平滑。

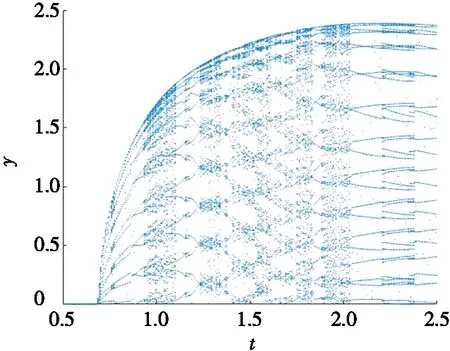
(a) 原系统局部分岔图

3 应用

超混沌系统因复杂度高，状态轨迹及系统产生的混沌信号难以预测，被广泛应用到图像加密、信息安全等领域。利用混沌映射自身的性质生成密码，从而完成对传输信息加密的目的[21]。 基于文献[22]提出对图像加密安全性的改进算法，将新超混沌系统应用到图像加密中，通过MATLAB软件仿真，观察图像的加密效果。

3.1 加密效果分析

取新系统的系统参数a=35,b=3,c=33,d=8，初值x0=1,y0=1,z0=1,w0=1，步长h=0.01，图像大小为256×256，用MATLAB软件进行仿真实验。与传统行列加密算法对比，分析Lena图像的加密效果。图6为加密算法对比分析。由图6a可以观察到：该算法较传统行列加密算法对Lena图像加密效果明显，密文图像杂乱似雪花，行加密和列加密图像似条状。图6b纵坐标表示像素点出现的次数，可以观察到明文直方图波动起伏较大，密文直方图像素出现的次数大致分布在750左右，分布均匀无较大波动，表明该算法成功将像素点置乱，行加密和列加密直方图与明文直方图相似，加密效果差。说明该算法与新超混沌系统结合，对图像的加密效果良好，扰乱性及安全性较高。

(a) Lena加密图像对比

3.2 安全性分析

(Ⅰ)敏感性分析。超混沌系统对初值十分敏感，该算法的密钥空间为1056，密钥空间越大，抗攻击能力越强。在解密过程中，若密钥发生微小的变化，加密图像将得不到正确解码图像。例如，将混沌初值x0进行10-14的微小变化，观察密文的解密效果。图7为密文图像的正确解密与错误解密对比。由图7可知：正确解密可以使原图恢复，错误解密则不能恢复原图，说明图像加密算法的密钥敏感性强，抗密钥攻击能力强。

(a) 正确解密

(Ⅱ)对图像进行相关性分析。相关性系数越趋近于0，说明相邻像素的相关性越差，表现在密文图像上则说明该算法的安全性较高，抗攻击能力强；相关系数接近于1，则反之。相关性系数计算公式为：

(19)

其中：x,y为像素点的灰度值。经计算密文图像在水平、竖直、对角方向的像素相关性都趋近于0，表明该算法的置乱性强，安全性高。图8为相邻像素的相关性相图，图8a中明文图像在水平、竖直、对角3个方向像素点具有明显的线性相关性；图8b中密文图像3个方向的像素点杂乱分布在矩形框中，像素点无相关性。说明该算法的安全性高，抗攻击性能强。

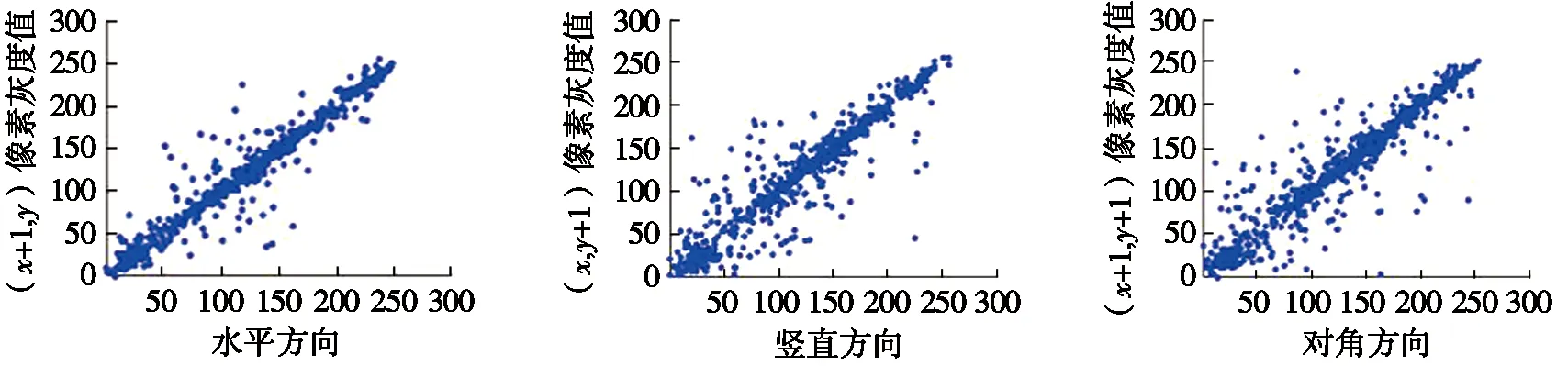
(a) 明文相关性相图

4 结论

(1)新系统发生超临界Hopf分岔，在时滞分岔点τn附近系统呈现出不同的稳定性。

(2)添加线性控制器后，时滞分岔点由0.673 9延迟至0.722 9，使得时滞扰动引起的Hopf分岔得到了有效延迟控制。

(3)与传统的行列置换加密方法相比较，该超混沌加密算法的加密性更好，有较好的安全性及抗攻击能力。