专注一题 通晓一类*
俞杏明 (江苏省兴化中学 225700)
石志群 (江苏省泰州教育局 225300)
经典试题反复研磨,不仅对试题认识越来越透彻,而且能归结出这一类问题的解决之道.同时还能实现试题解答者到试题编制者的角色转换.
1 经典试题永恒零点
例1(2013·江苏)设函数f(x)=lnx-ax,g(x)=ex-ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
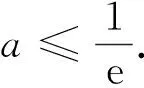
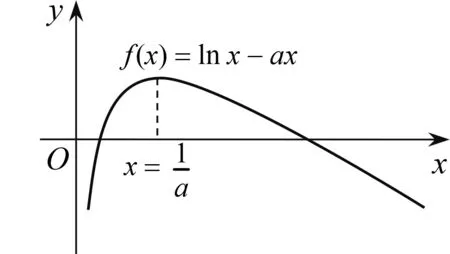
图1
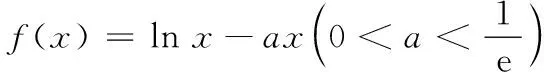
2 微处着手查找关系
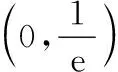
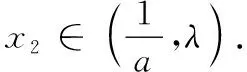
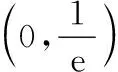
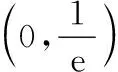
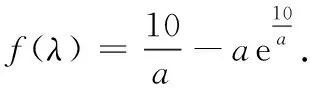
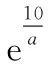
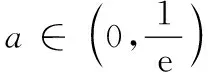
3 整体入眼知识迁移
由于参数a的不确定性,因此只能运用极限拟合思想生成函数f(x)的图象.笔者惊奇地发现,函数(*)的图象极值点左偏(图1).
下面要寻求函数f(x)右零点x2所在区间,可以先寻求x1+x2的一个上界,也就是寻求与函数f(x)共零点且极值点右偏的函数,因此需扭转函数f(x)的极值点偏移方向[2].
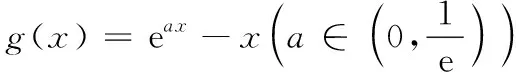
下面接例1未完的解答继续作答.
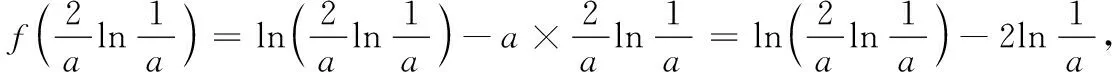
4 内部透视局部放缩
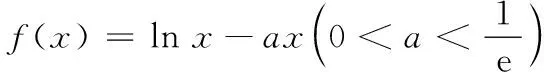
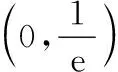
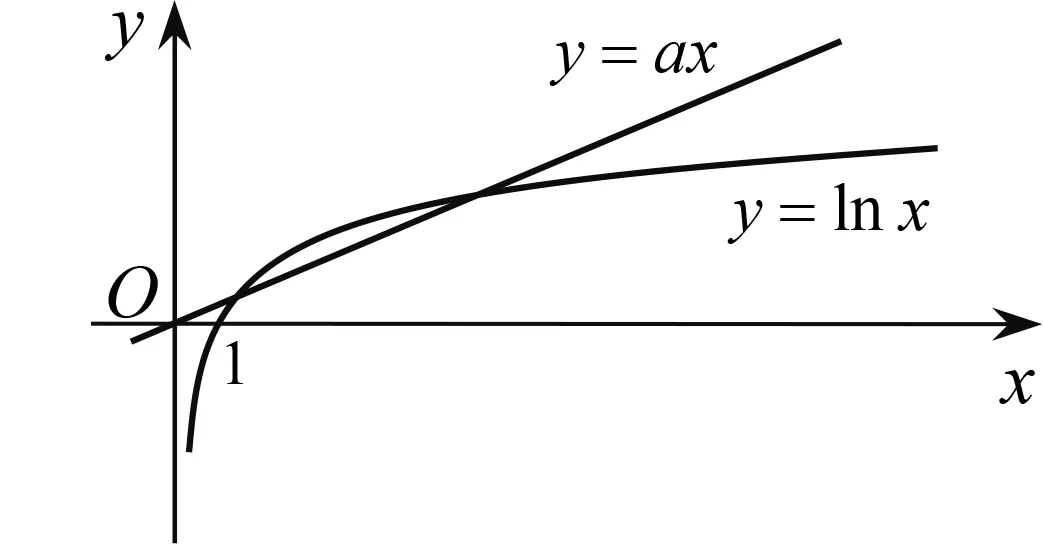
图2
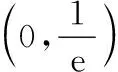
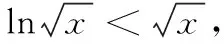
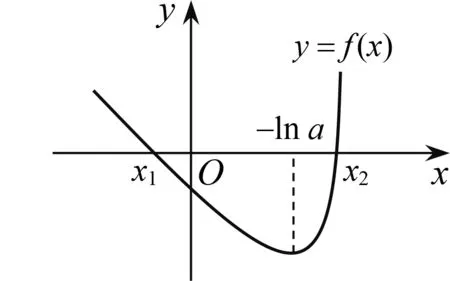
注意到图2中,y=ax与y=lnx的图象在y轴右侧较远处存在空隙,且随着x的值增大,空隙变大.因此笔者考虑构造中间函数y=mxn(m>0,0 图3 细细琢磨,极值点偏移法长于整体思考,中间函数法适合局部放缩,变换主元法精于微观探查.三种手段能够使含参函数零点区间得到全方位查找. 例2(2017·课标I)已知函数f(x)=ae2x+(a-2)ex-x. (1)讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. 解(1)当a≤0时,f(x)在(-∞,+∞)上单调递减;当a>0时,f(x)在(-∞,-lna)上单调递减,在(-lna,+∞)上单调递增. 下面探寻f(x)在(-lna,+∞)上右零点x2所在的区间(图4). 图4 方法1 将f(x)整理为f(x)=a(e2x+ex)-2ex-x.把x看成常数,则a在(0,1)上取越来越小的值时,f(x)越来越小.这表明a在(0,1)上变小时,y=f(x)图象上每一点均下移,因此x2变大,零点x2为关于a的单调递减函数. 接例2未完的解答继续作答. 接例2未完的解答继续作答. 方法3 把f(x)=ae2x+(a-2)ex-x(a∈(0,1))整理为f(x)=a(e2x+ex)-(2ex+x),拆分出两个函数y=a(e2x+ex)(a∈(0,1))与y=2ex+x,但这两个函数均为下凸函数,中间过渡函数难以寻求.令ex=t,则f(x)整理为g(t)=a(t2+t)-(2t+lnt)=at2+(a-2)t- lnt.把g(t)拆分为y=at2+(a-2)t(a∈(0,1))与y=lnt,显然这两个函数分别为下凸函数与上凸函数. 下面通过中间函数y=t证明g(t)存在右零点. 上述方法手段逆向应用,能够多渠道生成这类试题.如构造上凸函数y=a(2x+lnx)(a∈(1,+∞))与下凸函数y=x2+x,组合出f(x)=a(2x+lnx)-x2-x,再把f(x)表达式中的字母重新排序,隐藏编制的痕迹,从而有下面这一试题: 例3已知f(x)=alnx-x2+(2a-1)x,当a∈(1,+∞)时,证明函数f(x)有且仅有两个零点. 还可以进一步隐藏编制的痕迹,在例3中把x换成ex,从而有下面的试题:已知f(x)=ax-e2x+(2a-1)ex,当a∈(1,+∞)时,证明函数f(x)有且仅有两个零点.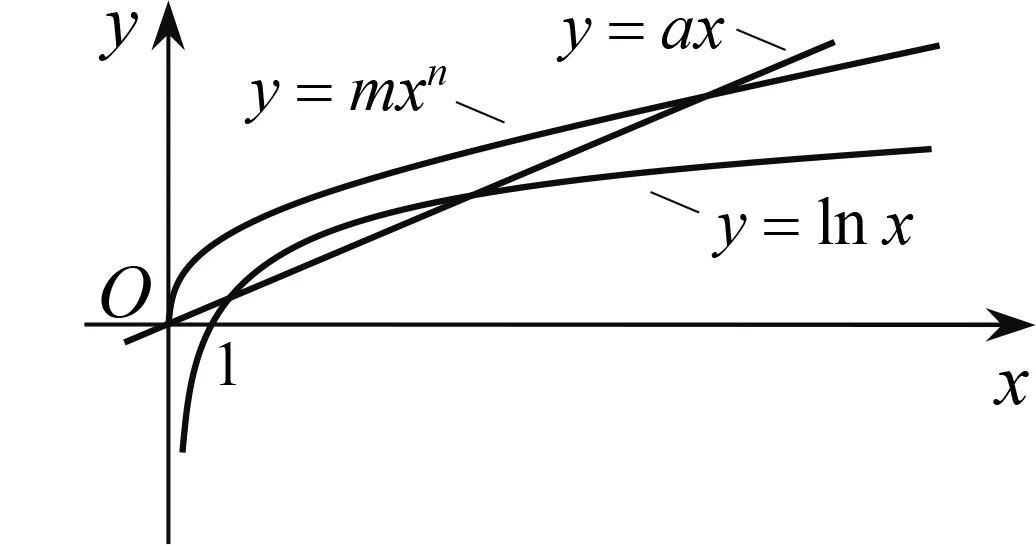
5 感悟提炼实战检验
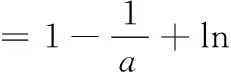
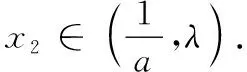
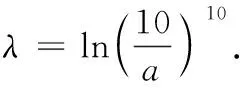
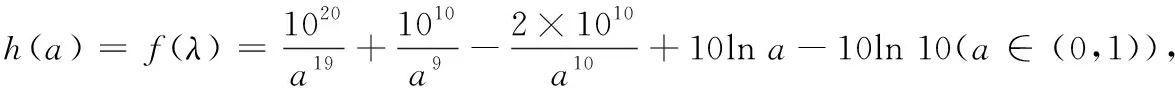
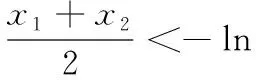
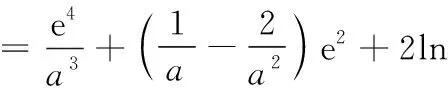
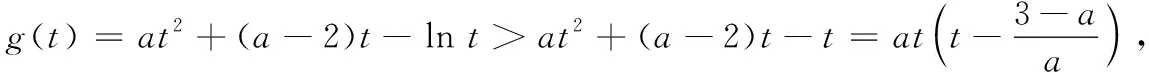
6 逆向应用编制试题

