液化场地装设粘滞阻尼器的桩基-结构体系抗震性能分析
司盼,唐亮,张征,邢东亮,吕卫清,凌贤长
(1.哈尔滨工业大学土木工程学院,黑龙江 哈尔滨 150090;2.黑龙江省寒区轨道交通工程技术研究中心,黑龙江 哈尔滨 150090;3.山东港口青岛港集团有限公司,山东 青岛 266005;4.中交第四航务工程局有限公司,广东 广州 510230;5.青岛理工大学土木工程学院,山东 青岛 266033)
引言
桩基础可以穿过软弱土层,把上部结构的荷载传递到更坚实的地基上,已被广泛应用到高层建筑、桥梁、和海洋平台等建筑物中[1]。随着我国桩基建设的蓬勃发展与抗震的迫切需要,桩基结构的抗震性能已经成为岩土工程抗震的研究热点。特别是,我国地处环太平洋地震带和欧亚地震带之间[2],地震灾害问题严重,如何改善强震作用下桩基结构抗震性能,已成为我国亟待解决的关键科学问题。
1972年,Yao[3]首次提出土木工程结构控制的概念,之后这个领域不断成熟,直到1994年8月在洛杉矶举行的第一届世界结构控制会议达到顶峰。消能减震技术是通过附加消能减震装置提高结构阻尼,使结构响应控制在预期范围内的结构控制技术。众多消能装置中,粘滞阻尼器具有在较宽频域内可运动的位移、不产生温度应力、阻尼力与位移滞后等优点而被广泛应用到改善桩基结构地震响应领域中[4]。Jin等[5]研究了粘滞阻尼器对桩基桥梁减震性能的影响,发现非线性粘滞阻尼器的减震性能更为理想。Han等[6]建立了考虑桩-土相互作用的单塔斜拉桥数值模型,并开展了粘滞阻尼器参数敏感性,发现摩擦摆隔震支座与粘滞阻尼器并联使用可以同时控制上部结构位移和桩墩地震响应。Yang等[7]采用振动台试验和有限元模拟相结合的研究手段,分析了桩-土-结构相互作用对采用粘滞阻尼器的桩基结构地震响应的影响,研究表明:忽略桩-土-结构相互作用会导致上部结构地震响应失真,且放大了非线性粘滞阻尼器的减震性能。Zhao等[8]通过发展简化数值模拟方法,分析了桩-土-结构相互作用对桩基-结构中阻尼器工作性能的影响。贾毅等[9]研究了顺桥向装设粘滞阻尼器降低桥梁固定墩地震响应的效果,并开展了粘滞阻尼器参数敏感性分析,选择参数最优值以提高减震效果。综上所述,国内外针对粘滞阻尼器在桩基结构应用方面已经开展了大量的研究工作。然而,针对液化场地且考虑桩-土相互作用的情况,粘滞阻尼器的适用性以及减震效果的研究近乎空白,致使现阶段对液化场地粘滞阻尼器减震设计的认识还较为模糊。
鉴于此,文中针对液化场地群桩-土-结构动力相互作用离心机试验建立三维有限元模型,将粘滞阻尼器布置在上部结构与柱墩顶部之间,研究粘滞阻尼器对液化场地桩基结构的影响规律和减震效果,并分析粘滞阻尼器力学参数敏感性,揭示上覆非液化土层对液化场地粘滞阻尼器减震设计的影响规律,得到非液化场地与液化场地粘滞阻尼器减震设计的异同。研究结果对液化场地桩基-结构粘滞阻尼器减震设计具有重要的指导意义。
1 液化场地装设粘滞阻尼器的桩基-结构减震性能分析数值模型
1.1 液化场地桩基地震反应离心机试验数值模拟与验证
基于Wilson[10]完成的液化场地群桩-土-结构动力相互作用离心机试验为原型建立三维数值模型。如图1所示,试验土层均选用饱和内华达砂,水位线位于地表处。2×2群桩基础采用空心铝管桩模拟钢管桩,桩长16.8 m,桩径0.67 m,壁厚19 mm,桩的弹性模量为70 GPa。柱墩高10.9 m,承台平面尺寸为4.6 m×4.6 m×2.3 m。在柱墩顶部固定一质量块,重量为2 000 kN,模拟上部结构的惯性作用。试验采用Kobe波作为基底输入地震动,峰值为0.22 g,地震动时程如图2所示。

图1 离心机试验示意图[10](单位:m)Fig.1 Schematic layout of centrifuge test[10](Unit:m)

图2 输入地震动[10]Fig.2 Base input motion[10]
模型中,饱和砂土的有限元模拟选用水-土耦合的六面体线性等参单元,本构模型选用能够模拟砂土液化特性和累积剪切变形特性的多屈服面塑性本构模型,饱和砂土的计算参数见表1[11]。由于试验本身的对称性,取一半试验体建立数值模型,模型长51.0 m×宽10.5 m×高20.5 m(见图3(a))。桩和柱墩均采用梁柱单元模拟。在桩-土刚性连接的基础上,增加零长度单元,并赋予零长度单元桩-土接触面属性,近似模拟桩-土摩擦滑移机理[12]。需要说明的是,采用砂土本构近似模拟承台,并赋予其较大的粘聚力、剪切模量和体积模量,使其在运算过程中处于弹性状态。为了模拟层状剪切箱边界特性,将模型垂直振动方向的两侧面位于同一高度的节点位移自由端绑定,并约束模型底部节点的竖向运动。将模型底部和侧面均设置为不透水边界,地表处土体孔压为零[13]。

表1 砂土本构模型计算参数[11]Table 1 Calculation parameters of sand constitutive model[11]

图3 有限元模型(单位:m)Fig.3 Finite element model(Unit:m)
图4对比了自由场土体和桩基结构响应的离心机试验结果和数值模拟结果。可以看出,超孔隙水压力计算值的波动形式、峰值点、稳定状态等均与离心机试验结果吻合较好;模拟结果基本再现了离心机试验中上部结构与饱和砂土加速度的时程特点。试验中,在桩身布置了5对应变片测量桩身弯矩,从图4可以看出桩身弯矩时程的波动形式与试验结果基本一致,从图5可以看出桩身峰值弯矩峰值分布的计算值与试验值吻合较好,表明有限元模型可以很好的再现强震下液化场地桩基动力响应结果。

图4 有限元模型可靠性验证Fig.4 Reliabily validation of the numerical element model

图5 桩身峰值弯矩的试验值与计算值Fig.5 Test value and calculation value of peak bending moment of pile
1.2 液化场地装设粘滞阻尼器的群桩-结构减震性能分析数值模型
目前,国内外学者针对粘滞阻尼器提出了多种力学模型来模拟其力学行为,主要有线性模型、Kelvin模型、Maxwell模型以及Wiechert模型等。当阻尼器为线性阻尼器时,采用线性模型与Kelvin模型描述其力学行为;当粘滞阻尼器内的流体含沥青材料等类似于粘弹性材料时,在低频率外荷载作用下将表现出稠化的特性,此时采用Wiechert模型;Maxwell模型包括非线性阻尼和线性弹簧两个部分,是一种刚度连续化模型,它可以准确反应出具有频率依赖性的粘滞阻尼器相关性质。
实际工程中,通常在柱墩顶部布置支座,为简化计算,采用zeroLength单元并赋予刚度很大的弹性材料模拟其竖向承载作用;粘滞阻尼器宜设置在相对变形或速度较大的位置,基于控制上部结构位移和柱墩底部地震响应的目的,将粘滞阻尼器一端与上部结构底部固接,另一端与柱墩侧面固接,详细布设位置如图6所示。根据已有研究成果[14-16],采用Maxwell模型模拟粘滞阻尼器的力学物理机制,建立液化场地装设粘滞阻尼器的桩基-结构有限元模型。地震作用下,粘滞阻尼器中活塞挤压内腔填充的粘滞流体,产生阻尼力。粘滞阻尼器出力F与活塞相对运动速度v关系如下式[17-18]:

图6 粘滞阻尼器布置Fig.6 Viscous damper layout

式中:C为阻尼系数;α为速度指数,当α取值为0~1时,为非线性粘滞阻尼器,当α等于1时,为线性粘滞阻尼器[19]。
图7给出了速度指数α分别为0.2、0.4、0.6、0.8和1.0时活塞运动速度-阻尼力关系曲线,可以看出,速度较小时,非线性粘滞阻尼器比线性粘滞阻尼器的出力大,随着速度的增大,线性粘滞阻尼器的出力增长速度明显高于非线性粘滞阻尼器。

图7 不同速度指数α情况下粘滞阻尼器的力-速度关系Fig.7 Force-velocity relations of viscous dampers with different velocity exponents α
2 参数敏感性与减震效果
2.1 参数敏感性
基于已建立的液化场地装设粘滞阻尼器的群桩-土-结构有限元模型,开展粘滞阻尼器的参数敏感性分析,以上部结构永久位移和柱墩底部峰值剪力作为评价指标,选取适用于液化场地粘滞阻尼器减震设计的阻尼系数C和速度指数α参数组合。为此,定义描述粘滞阻尼器降低结构体系地震响应的减震率E:

式中:N和Y分别代表非减震结构和减震结构的地震响应。
图8为阻尼系数C和速度指数α对上部结构永久位移减震率的影响,可以看出,当速度指数α=0.5~0.9、阻尼系数C=500~1 000 kN·m-α·sα时,粘滞阻尼器控制上部结构永久位移效果较理想。图9为阻尼系数C和速度指数α对柱墩底部峰值剪力的影响,可以看出,同一阻尼系数C时,随着速度指数α增大,柱墩底部剪力逐渐减小,致使减震率E升高;当保持速度指数α不变时,阻尼系数C越大,柱墩底部峰值剪力减震率越底,这更多可能是由于阻尼系数C的增大导致阻尼器出力增加(见图10),附加在结构上的作用力也越大。从图10可以看出,随着速度指数α的减小,阻尼器出力对阻尼系数C的敏感性逐渐增强。

图8 上部结构永久位移减震率随粘滞阻尼器参数的变化Fig.8 Variation of permanent displacement damping rate of superstructure with viscous damper parameters

图9 柱墩底部峰值剪力减震率随粘滞阻尼器参数的变化Fig.9 Variation of the peak shear damping rate at the bottom of column pier with the parameters of viscous damper
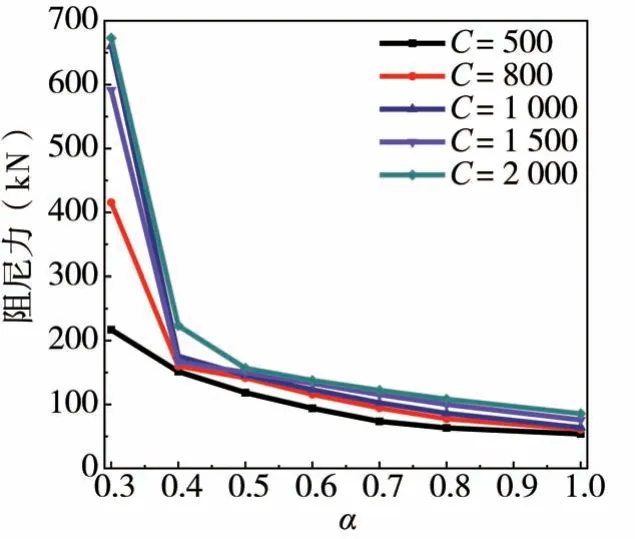
图10 阻尼器出力随粘滞阻尼器参数的变化Fig.10 Variation of the damper forces with viscous damper parameters
2.2 减震效果
基于同时控制上部结构永久位移和柱墩底部地震响应的目的,文中建议α取0.8,C取1 000 kN·m-0.8·s0.8。图11对比了非减震结构与减震结构的地震响应,可以看出,在柱墩顶部和上部结构之间布置粘滞阻尼器后,上部结构峰值加速度从0.37 g减小到0.23 g,减震效率为38%;上部结构峰值位移从153 mm减小到107 mm,减震率为30%;柱墩底部峰值剪力从130.59 kN减小到84.63 kN,减震率为35%;柱墩底部峰值弯矩从1 423.41kN·m减小到922.518 kN·m,减震率为35%;因此,粘滞阻尼器明显降低了上部结构的加速度和位移,减轻了柱墩底部剪力和弯矩响应,液化场地桩基-结构的抗震性能得到了明显的改善。图12为粘滞阻尼器的力-位移滞回曲线,可以看出,粘滞阻尼器滞回曲线饱满,表明粘滞阻尼器在液化场地可以有效消耗地震能量,衰减桩基-结构地震响应。

图11 非减震结构与减震结构地震响应对比(α=0.8,C=1 000 kN·m-0.8·s0.8)Fig.11 Comparison of seismic response between non-damping and damping structures(α=0.8,C=1 000 kN·m-0.8·s0.8)

图12 粘滞阻尼器的力-位移滞回曲线(α=0.8,C=1 000 kN·m-0.8·s0.8)Fig.12 Force-displacement hysteretic curve of viscous damper(α=0.8,C=1 000 kN·m-0.8·s0.8)
3 上覆非液化土层对减震设计的影响
地震作用下,场地发生液化的主要条件是加载在饱和土体上的剪切力超过了土体抗剪强度,而上覆非液化土层对可液化土体抗剪强度有一定的影响。为此,本节将Wilson离心机试验中2.3 m厚的松砂土层修改为黏土,研究上覆非液化土层对液化场地装设粘滞阻尼器的桩基-结构减震性能的影响规律。黏土选用多屈服面塑性本构模型模拟,该模型采用非线性滞回材料模拟粘土,具有米塞氏多屈服面运动塑性变形特性。黏土模型的计算参数见表2[20]。

表2 黏土本构模型计算参数[20]Table 2 Constitutive model parameters for clay[20]
图13和图14给出了上覆非液化土层条件下,上部结构永久位移和柱墩底部峰值剪力随粘滞阻尼器参数的变化。可以看出,与无上覆非液化土层工况不同,只有当速度指数α为0.6~1.0、C=500 kN·m-α·sα时,减震结构的上部结构永久位移小于普通结构。综合考虑减震效果,选取速度指数α=0.9、阻尼系数C=500 kN·m-0.9·s0.9作为上覆非液化土层工况中粘滞阻尼器减震设计的最优参数组合,以此对比粘滞阻尼器的减震效果。由图15可以得到,在柱墩顶部和上部结构之间布置粘滞阻尼器后,上部结构峰值加速度从0.26 g降低到0.21 g,减震率为20%;上部结构峰值位移从190 mm减小到80 mm,减震率达到56%;柱墩底部剪力和弯矩也明显下降,柱墩底部峰值剪力从167 kN降低到58 kN,减震率达到65%;柱墩底部峰值弯矩从1 827 kN·m降低到631 kN·m,减震率达到65%。
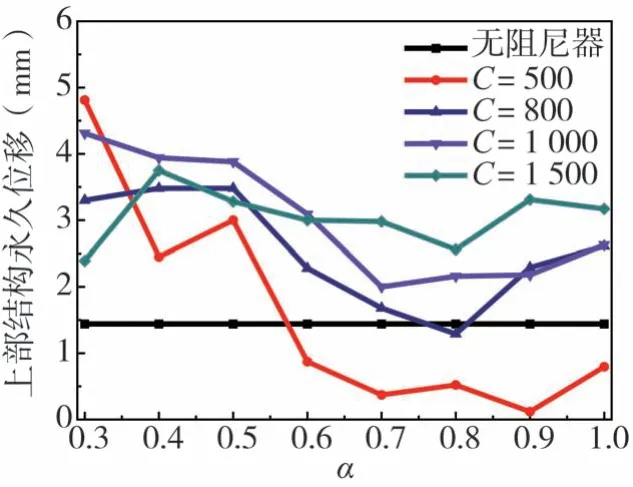
图13 上覆非液化土层工况中上部结构永久位移随粘滞阻尼器参数的变化Fig.13 Variation of permanent displacement of superstructure with viscous damper parameters in overlying non-liquefiable soil layer

图14 上覆非液化土层工况中柱墩底部剪力峰值随粘滞阻尼器参数的变化Fig.14 Variation of peak shear at the bottom of the pier with viscous damper parameters in overlying non-liquefiable soil layer
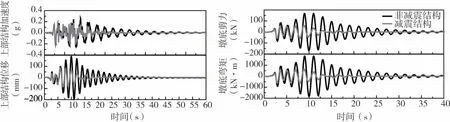
图15 上覆非液化土层工况中非减震与减震结构地震响应对比(α=0.9,C=500 kN·m-0.9·s0.9)Fig.15 Comparison of seismic response between non-damping and damping structures under non-liquefiable soil layer(α=0.9,C=500 kN·m-0.9·s0.9)
4 非液化与液化场地减震设计对比
基于已建立的液化场地装设粘滞阻尼器的群桩-土-结构动力相互作用数值模型,保持土体和桩基结构的其他参数不变,只增大饱和砂土的渗透系数,保证地震作用下孔隙水压力快速消散,避免土体液化,据此研究非液化与液化场地粘滞阻尼器减震设计的异同。图16和图17是粘滞阻尼器参数对非液化场地桩基结构地震响应的影响,可以看出,在速度指数α=0.5~0.9、阻尼系数C=2 500~5 000 kN·m-α·sα的范围内,选取合适的粘滞阻尼器参数组合,均可以控制上部结构永久位移和降低柱墩底部峰值剪力。

图16 非液化场地中上部结构永久位移减震率随粘滞阻尼器参数的变化Fig.16 Variation of permanent displacement damping rate of superstructure with viscous damper parameters in non-liquefaction ground

图17 非液化场地中柱墩底部峰值剪力减震率随粘滞阻尼器参数的变化Fig.17 Variation of peak shear damping rate at the bottom of the pier with viscous damper parameters in non-liquefaction ground
表3为非液化与液化场地粘滞阻尼器减震设计的对比,可以看出,非液化与液化场地速度指数α的适用值均在0.5~0.9之间,而阻尼系数C的适用值分别为2 500~5 000 kN·m-α·sα和500~1 000 kN·m-α·sα;粘滞阻尼器在非液化场地与液化场地控制上部结构永久位移的效果均较好;相比于液化场地,粘滞阻尼器在非液化场地控制柱墩底部剪力的效果较差,这更多可能是因为非液化场地粘滞阻尼器速率更大,导致粘滞阻尼器出力增大,反作用于柱墩底部的剪力也相应增大。

表3 非液化与液化场地粘滞阻尼器设计对比Table 3 Comparison of design of viscous dampers for non-liquefiable and liquefiable soil
5 结论
文中选用Maxwell模型模拟粘滞阻尼器的力学行为,分析粘滞阻尼器对液化场地群桩-土-结构体系的减震效果,甄选出适用于液化场地粘滞阻尼器减震设计的阻尼系数C和速度指数α组合。最后,分析了上覆非液化土层对液化场地粘滞阻尼器减震设计的影响,对比了非液化和液化场地粘滞阻尼器减震设计异同,主要得到以下结论:
(1)Maxwell模型可以有效地刻画非线性粘滞阻尼器的力学行为,证明了粘滞阻尼器在液化场地同样具有理想的减震效果,显著降低了桩基上部结构和柱墩底部的地震响应,提高了液化场地群桩-土-结构的抗震性能。
(2)上覆非液化土层改变了液化场地粘滞阻尼器减震设计的适用参数组合,速度指数α的适用值从0.5~0.9变为0.7~0.9,阻尼系数C的适用值从500~1 000 kN·m-α·sα变为500 kN·m-α·sα。
(3)非液化场地与液化场地粘滞阻尼器减震设计的速度指数α适用值均为0.5~0.9,而阻尼系数C的适用值分别为2 500~5 000 kN·m-α·sα和500~1 000 kN·m-α·sα;粘滞阻尼器在非液化与液化场地的上部结构永久位移减震率分别是41.0%和54.4%,柱墩底部剪力峰值减震率分别是7.0%和26.1%。
(4)文中研究均基于上层相对密度为35%的饱和松砂、下层相对密度为80%的饱和密砂、低承台与桩底自由的条件开展,因此,文中得出的结论用于工程实际的可靠性需要进一步分析验证。

