基于车－桥耦合振动的钢－混组合工字梁桥动力冲击系数研究

周中涛，王东升，王荣霞，张鹏颺，张蒙

（1.河北工业大学土木与交通学院，天津 300400；2.河北工业大学土木工程技术研究中心，天津 300400；3.河北省高速公路延崇管理中心，河北 张家口 075000）

引言

在我国新建公路桥梁中，钢－混组合工字梁桥以其自重轻、承载力好和造价合理等优点受到重视。车－桥耦合振动效应是桥梁设计必须考虑的因素，我国现行《公路桥涵设计通用规范：JTG D60－2015》［1］中以冲击系数（IM）考虑车辆与桥梁之间的动力相互作用，其计算公式为桥梁基频的函数。因钢－混组合工字梁桥在国内发展较新，关于动力冲击系数的研究尚少。

动力冲击系数的研究一类方法是采用实桥测试（跑车试验），另一类方法则借助于车－桥耦合振动的数值分析，而后者可以考虑的因素更多，事实上有关车－桥耦合振动数值模拟的研究也异常活跃。Yang等［2］提出了一种用于分析桥梁－车辆系统动力响应的迭代求解方法；Yang等［3］用该方法获得了高速列车作用下简支梁动态响应的解析解；Lu等［4］运用ABAQUS软件，在验证前述解析解的基础上，建立起列车－桥梁耦合的有限元模型框架，并建立起日本新干线列车与桥梁的动力相互作用模型，桥梁的动力反应结果与试验数据对比表明该框架模型具备可用性。Kwasniewski等［5－6］使用LS－DYDA商业软件开发了一个有限元卡车模型，考虑了其3D悬挂系统，平动和转动车轮及合适的轮桥接触算法等，以一座3跨连续预应力T梁桥为工程背景，结合试验数据指出卡车在引桥处跳车会触发负载反弹，从而给桥梁造成更大的动力冲击效应。González等［7］认为现行的研究方法一般是先计算静载效应，然后应用一个放大因子来考虑动载效应，这忽略了静载效应极值和动载效应极值同时发生的概率降低问题，类似发现在Caprani等［8］的研究中也被证实。Brady等［9－10］通过对一简支梁桥在单车辆及车队分别作用下的研究，确定了桥梁动力冲击系数达到峰值时车辆的临界行车速度，分析讨论了车队作用下同向行驶和车间距等因素对桥梁冲击系数的影响。Law等［11］发现多跨连续梁桥在车辆荷载作用下，每跨动态响应不同，这种差异在车辆制动作用下会更大，因此对车辆制动时的冲击系数更精准的定义，应该是基于对同一跨度的最大动态和静态响应的比较。Obrien等［12］通过建立三维车辆与板梁桥有限元模型，考虑路面不平整度与车队特性，发现现行的大多规范对IM值的计算偏于保守，进而提出使用（assessment dynamic ratio，ADR）代替冲击系数去考虑车辆与桥梁间的动态响应。

近些年国内学者对车－桥耦合作用研究也较为广泛［13－15］，涉及诸多因素的影响，包括桥梁结构（如跨度和固有频率）、路面不平整度、车辆悬挂系统和车辆重量等，研究它们对不同桥梁IM值的影响［16－17］。张楠等［18］系统研究了列车－桥梁耦合动力系统的分析方法，其车辆子系统模型以刚体动力学方法建立，桥梁子系统模型以有限元方法建立，竖向与横向轮轨关系分别以轮轨密贴假定和Kalker线性蠕滑理论定义，车桥耦合动力方程以全过程迭代法求解，讨论了高速列车通过我国按标准化设计桥梁的动力响应，计算了车速200～400 km/h范围内车辆与桥梁子系统的动力响应。张鹏等［19］发现存在一个使跨中位移均方根响应峰值突然减小的速度临界值，其值大小与边界条件和桥面等级无关。亓兴军等［20］提出采用过桥车辆振动响应来识别桥梁自振特性的间接测量法，发现车速会影响桥梁振型识别的精度。周云等［21］提出了一种基于大数据与区间仿射算法的中小桥梁结构影响线非接触识别方法，并采用车桥耦合数值模拟对其有效性进行了验证。Han等［22］利用自主开发的桥梁动力分析软件BDANS建立起车－桥耦合系统，用激光道路测试车测量四组路面不平整度并将其输入，分析左右轮一致激励与否对结构响应的影响。邓露等［23－24］基于车－桥耦合振动理论，在桥梁截面类型、桥跨长度和车辆制动位置等影响因素方面做了大量数值分析与试验工作，给出了中小跨径混凝土简支梁桥IM的建议取值。高庆飞等［25］采用综合模态法研究多跨梁桥在移动车辆作用下的动力反应，发现边跨、侧跨和中跨IM值受桥梁跨数的影响规律，并指出现行规范中的IM值由于没有区分桥跨位置而不够合理。何维［26］通过大量数值模拟探讨了桥梁截面类型、支承方式、路面等级和桥梁跨径等因素，以及车辆类型、车辆参数、行车速度等对桥梁动力冲击系数的影响，并发现不同主梁材料的桥跨动力特性存在不同，由此导出的动力冲击系数也具有较大差异，影响因素也不完全相同。

我国规范对IM的计算方法源于上世纪90年代李玉良［27］教授使用动态测试系统，连续观测7座跨径不同、初始条件不同的钢筋混凝土桥梁，采集了6 600多个具有代表性的IM样本，并将保证率95%的数值进行回归分析，拟合得到冲击系数与桥梁自振频率之间的关系曲线并沿用至今。然而该研究所选择桥梁类型不包括钢－混组合工字梁桥。文中以延崇高速新建公路桥梁Y078主线桥为工程背景，该桥为3×40 m跨工字钢－混凝土组合工字连续梁桥。在实桥静载试验和动载试验基础上，运ABAQUS软件建立3轴车辆与桥梁相互作用数值模型，考虑了车辆速度以及路面不平整度等因素，基于车－桥耦合振动理论分析了在不同工况下IM值的分布规律，最后提出类似跨径下钢－混组合工字梁桥IM值的建议取值及其所属概率分布。

1 车－桥耦合振动分析模型

1.1 桥梁模型

文中所选取桥梁为一新建高速公路连续梁桥，桥梁跨径布置为：3×40 m，全桥共1联，桥梁全长128.5 m，上部结构采用钢－混工字组合梁，由外露的工字型主梁通过连接件与钢筋混凝土桥面板组合而成，共4片主梁，桥面全宽12.24 m，钢主梁之间通过横梁加强横向联系，横梁标准间距为5.0 m，现场实桥照片见图1。利用有限元软件ABAQUS中的壳单元建立了桥梁的三维有限元模型，考虑了厚度为8 cm的混凝土铺装层和10 cm的沥青混凝土铺装层，以绑定约束的方式与桥面板连接，建立的桥梁有限元模型及桥梁横截面尺寸见图2。

图1 钢混组合工字梁桥现场照片Fig.1 Site photo of steel-concrete composite I-beam girder bridge

图2 桥梁模型Fig.2 Model of bridge

1.2 车辆模型

3轴车辆模型被简化为由一系列弹簧和阻尼装置连接的刚体组合，车辆车体、车轴、车轮左右对称。该车辆的数值模型如图3所示。对于图3中的3轴车辆，整个车辆由7个刚体组成，并具有9个独立的自由度，即6个车轮的6个垂直自由度，以及车身的一个垂直、侧倾和俯仰自由度。车辆参数的取值根据参考文献［28］及文中试验用车辆共同确定，见表1。

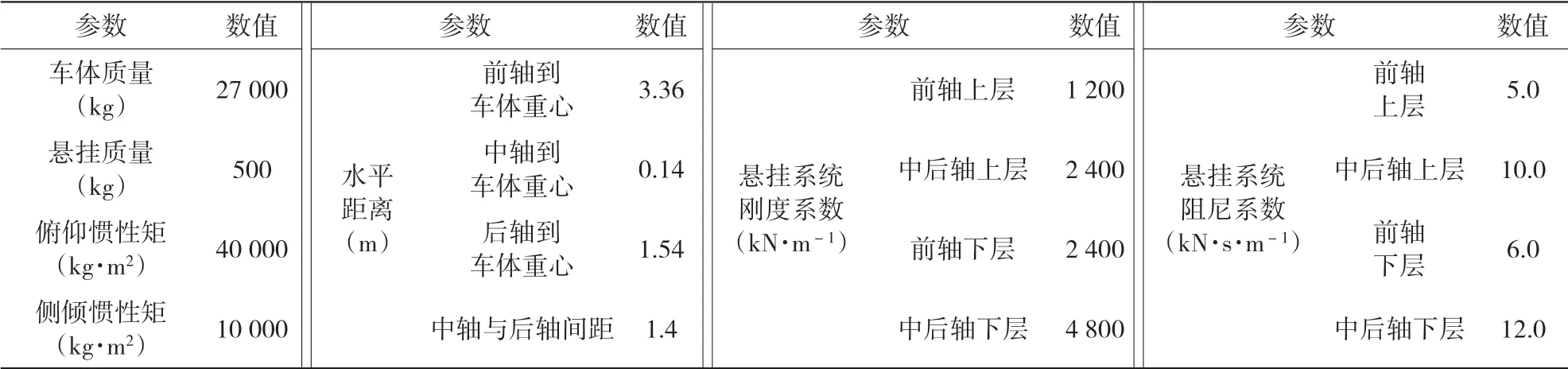
表1 3轴9个自由度车辆模型参数Table 1 Parameters of 3-axis 9-DOF vehicle model

图3 3轴车辆模型Fig.3 Model of 3-axis vehicle

1.3 路面不平整度

路面不平整度是引起车桥振动的主要激励源，国际标准化组织（ISO）将路面不平整度划分为8个等级，从A到H路面平整度逐渐变差。我国对路面平整度的规范《机械振动道路路面谱测量数据报告（GB/T 7031－2005）》等同于《ISO 8608：1995（E）》［29］。在数值模拟中，路面不平整度的生成通常被假定为均值为0的高斯平稳随机过程，其通常由功率谱密度函数（PSD）的傅里叶逆变换（IFFT）生成。路面不平整度的表达式为：

式中：θk为服从0～2π均匀分布的随机相位角；Gd（nk）为桥面不平整度功率谱函数；nk为空间频率；Δn为空间频率采样间距。

ISO 8608：1995中规定功率谱函数表达式为：

2)不同积云参数化方案对不同量级降水预报的优劣不同,且没有一种积云方案对所有量级降水预报结果都较优。对于24 h累积降水,SAS方案的RMSE和ACC较优,G3D的ACC评分较高,但是RMSE也较大;小雨量级的TS评分,Tiedtke方案结果较好,GD方案次之;中雨量级的TS评分,KF方案优于其他,SAS方案次之;大雨量级的TS评分,SAS方案最优;暴雨量级的TS评分,GD方案较优,SAS方案最差。对于6 h和3 h的累积降水,SAS方案的RMSE和ACC评估结果较优,Tiedtke方案的TS评分结果较优。整体来看,SAS、Tiedtke、GD积云参数化方案预报的结果较稳定。

式中：n为空间频率，单位m－1；n1、n2为截止频率的上、下限；n0为参考空间频率，取0.1 m－1；Gd（n0）为参考空间频率n0下的路面谱值，称为路面不平顺系数，单位m2/m－1；ω为频率指数，为双对数坐标上斜线的频率，决定路面谱的频率结构，一般取2.0。

文中选取B等级路面平整度以符合试验桥梁的实际情况，利用Yao等［30］的方法实现路面平整度在工程软件中的模拟，为消除路面不平整度生成过程的随机性对计算结果的影响，在每种工况下，生成40组随机路面，并进行车桥耦合振动数值模拟，而后对这40次运算结果进行统计分析。其中一组路面不平整度样本见图4。

图4 B等级路面不平整度曲线Fig.4 Grade B road surface roughness curve

1.4 车－桥系统动力学方程

车桥耦合系统的动力学方程［31］如下：

式中：M、C、K为质量、阻尼、刚度矩阵；u、u̇、u¨为系统位移向量、速度向量和加速度向量；下标b、v分别代表桥梁、车辆；Fvg为车辆自身重力；Fbr、Fvr为耦合体系间分别作用于桥梁、车辆上的相互作用力，其大小相等方向相反；下标r、g分别表示车桥耦合振动相互作用力和车辆自重。

作用于桥梁结构上的外荷载由2部分组成：

式中：Fvg与车辆的运动无关；Fbr则随着车辆在桥梁上的不断移动而随之变化。

车辆与桥梁在接触点i处的相互作用力Fvr可由下式表达：

文中的车辆与桥梁模型均在ABAQUS中建立，运用罚函数实现车辆与桥梁之间的动力相互作用，在该系统模型建立之后，使用ABAQUS内嵌的Hilber－Hughes－Taylor－α（HHT－α）方法计算系统在当前分析步的运动向量：位移、速度和加速度。HHT－α时程积分方法是在Newmark－β算法的基础上发展起来的隐式算法，在ABAQUS动力隐式直接积分方法采用了这一递推格式［4］。

1.5 车－桥系统模型验证

在现场静载试验中，在桥梁中跨及边跨跨中处，分别对称布置2辆车、4辆车及6辆车，车重均为30 t，车辆静态布置见图5，布置顺序见表2。记录不同工况下桥梁测点的挠度值，在数值模型中复现以上工况并计算同一测点挠度值，试验与模拟的桥梁挠度值见表3，可见桥梁有限元模型静力反应与实桥测试较为吻合。本项目还进行了脉动下的桥梁动力特性的测量，表4给出了与桥梁前三阶实测竖向频率与数值模拟结果的对比，它们也较为吻合。

表4 脉动试验下桥梁前三阶竖向频率Table 4 The first three orders of vertical frequency of the bridge under pulsation test

图5 静载车辆布置Fig.5 Layout of vehicle for static loading test

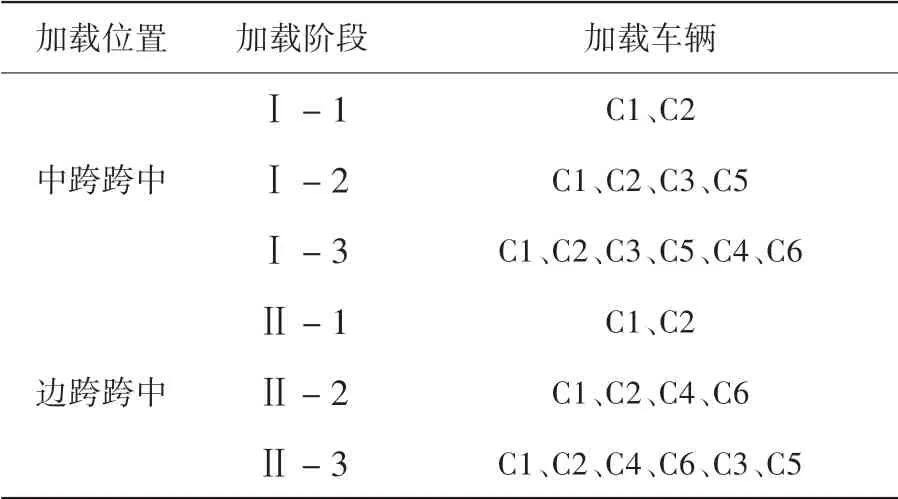
表2 静载车辆加载顺序Table 2 Static load vehicle loading sequence

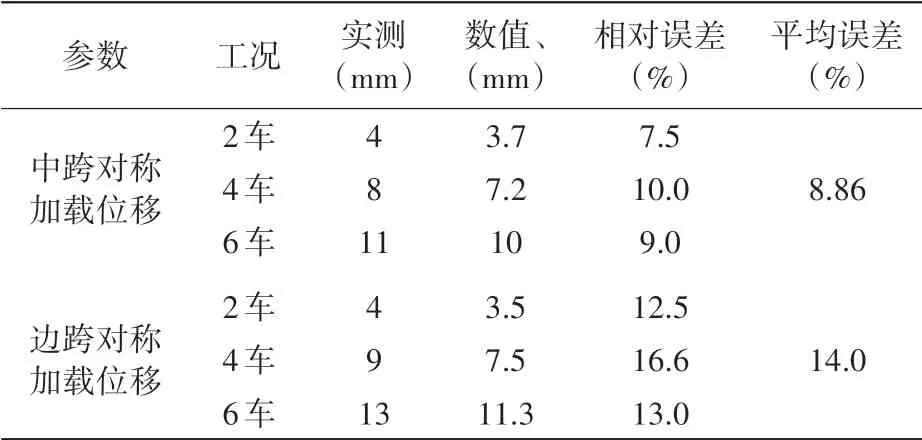
表3 静载试验及数值模拟下桥梁测点挠度Table 3 Deflection of bridge measurement points under static load test and numerical simulation

在对车辆－桥梁动力相互作用的模拟中，先进行了“跳车”试验过程的模拟，以进一步验证模型的准确性。数值模拟过程与“跳车”试验过程一致：总重30 t的单辆车以5 km/h的速度缓慢驶向桥梁，在边跨跨中及中跨跨中的行车道上分别放置一条尺寸100（长）×10（宽）×10（高）cm的木枕，当车轮压上木枕瞬间与离开木枕瞬间，车辆均停留数秒以模拟跳车现象。由测得的试验数据所计算的IM值见表5，由数值模型所得到的IM值（见表6），二者所得到的的IM值误差在3.38%之内。

表6 数值模型跳车工况IM值Table 6 IM value of jumping car case in numerical simulation

综上，数值模拟与实梁静载试验和“跳车”试验的实测结果误差较小，吻合度较高，再结合后文2.2节中“跑车”试验的模拟结果，可认为文中车－桥耦合振动数值模型是可靠的。

2 冲击系数概率分布及影响因素

2.1 冲击系数定义

桥梁冲击系数的物理定义式为：

式中：Ydmax为动载作用下该测点最大动挠度值；Yjmax为相应静载荷作用下该测点最大挠度值，简称最大静挠度值，其值可由动挠度曲线求得：

式中：Ydmin为动载作用下该测点最小动挠度值；其余参数同上。

影响公路桥梁冲击系数的因素大致可总结归纳成以下3类：（1）车辆荷载本身的几何与动力特性；（2）桥梁结构的几何与动力特性；（3）激振与冲击条件等。由于模拟随机车流、桥梁激振及车辆行驶位置对冲击系数的综合效应较为复杂，作为钢－混组合工字梁桥冲击系数初步研究工作，文中将IM视为连续随机变量概率模型，在车－桥耦合振动计算中仅考虑了路面不平整度样本及车辆行车速度因素。

2.2 冲击系数试验和数值比较

在实桥“跑车”试验中，以总重30 t的单辆车分别以20、30、40、50 km/h的速度驶过桥梁，由测得试验数据计算所得到的边跨跨中及中跨跨中IM值见表7。

表7 “跑车”试验和数值模拟IM值Table 7 IM values between the moving loading test and the simulation

在车－桥耦合振动数值模拟中，运用MATLAB软件及采用傅里叶逆变换（IFFT）生成1组不平整度，计算得到的桥梁中跨跨中测点的位移时程，以及实桥“跑车”试验测得结果见图6，可见数值模拟与实测的位移时程较为符合。边跨数值模拟与试验结果与此一致，限于篇幅，不再给出。

图6 实桥中跨位移时程实测和模拟比较Fig.6 Displacement time history of the bridge in the middle-span for moving loading test and simulation

2.3 冲击系数概率分布

采用傅里叶逆变换（IFFT）随机生成40组路面不平整度，将其导入ABAQUS的车－桥耦合振动分析模型中，求得桥梁中跨跨中及边跨跨中处最大动挠度值，并计算相应静载作用下最大静挠度值，由式（6）和式（7）计算各速度下各组路面不平整度的IM值。

通过对计算得到的IM值进行卡方优度拟合检验发现，算例桥梁中跨跨中IM值的概率分布服从正态分布，算例桥梁边跨跨中IM值的概率分布服从对数正态分布，样本频率直方图及拟合函数直方图分别见图7和图8。正态分布和对数正态分布的分布函数分别见式（8）和式（9）：

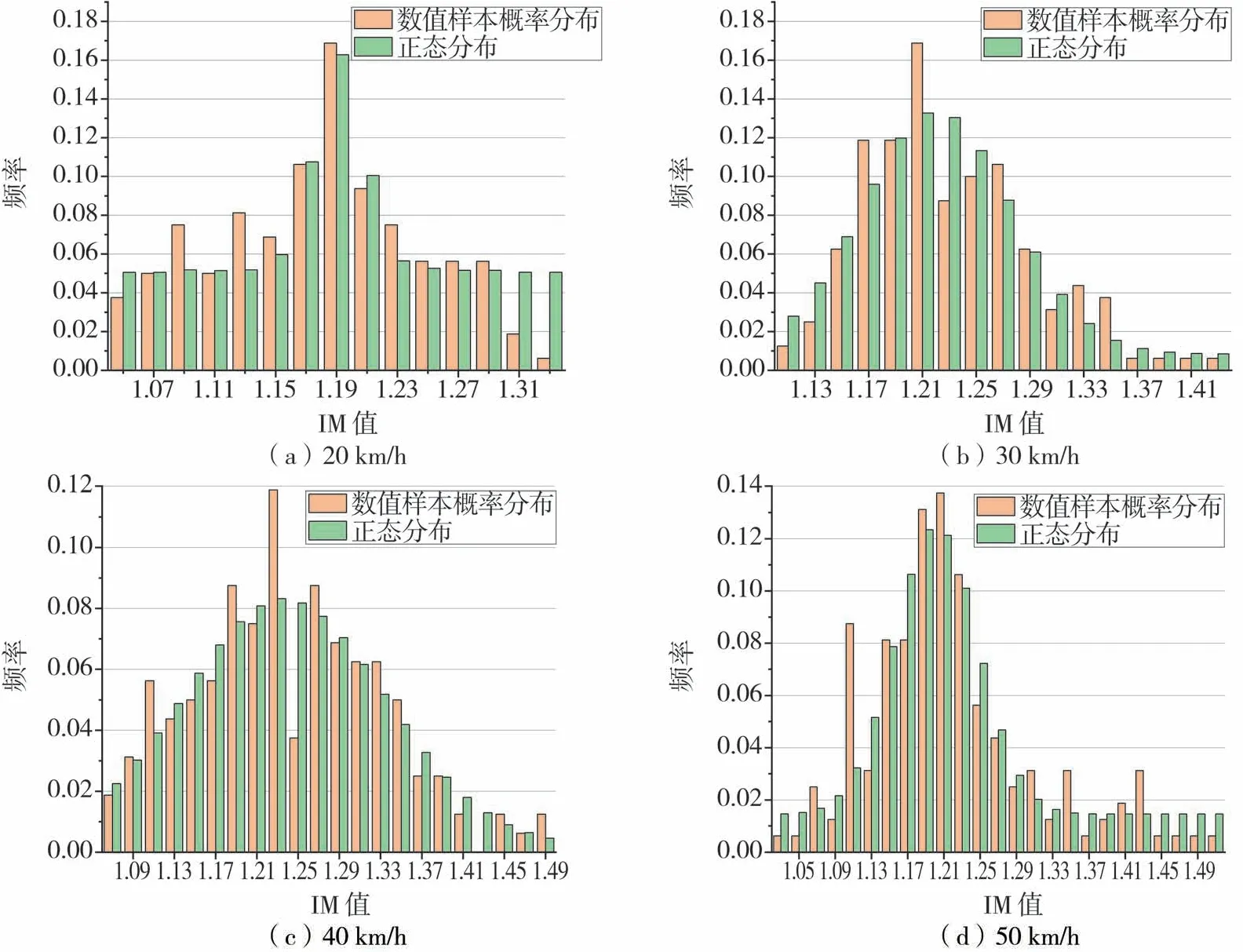
图7 中跨冲击系数IM频率直方图Fig.7 Frequency histogram of the mid-span impact coefficient IM

图8 边跨冲击系数IM频率直方图Fig.8 Frequency histogram of the side-span impact conefficient IM

式中：y为频率值；x为IM值；y0、xc、ω、A为常数。

依据数值模拟结果，文中给出了不同速度工况下中跨和边跨IM概率分布函数的的取值，见表8。同时，根据皮尔逊χ2拟合检验理论，表9给出了拟合函数的χ2值和拒绝域阈值，可见文中所拟合的8组函数的χ2值均小于拒绝域阈值，可以接受。它们可为今后同等跨径钢－混工字组合梁桥IM值可靠概率研究提供参考，亦可为工程设计提供依据。

表8 y0、xc、ω、A的取值Table 8 Value of y0、xc、ω、A

表9 拟合函数卡方值及其拒绝域阈值Table 9 Chi-square and its rejection threshold of fitting function

对以上各速度工况下中跨和边跨的IM分布拟合函数，求其数学期望作为第1组IM值；取数值模拟结果的算术平均值作为第2组IM值；3次实桥“跑车”试验结果的算术平均值作为第3组IM值。以上3组IM值的比较见图9，可以看出：（1）随着车辆速度的增加，IM值呈现先增大后减小的趋势，算例工况车速为40 km/h时IM值达到极值；（2）在车辆速度相同情况下，文中算例桥梁中跨的IM值较之边跨IM值略大；（3）拟合分布函数较之算术平均的IM值与试验结果要接近，故在对数值模拟IM值结果的处理中，采用合适的概率分布函数先拟合，比直接采取算术平均方法更合适些。

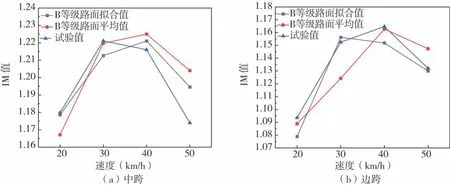
图9 3组IM值比较Fig.9 Comparison of three groups of IM

其他说明，若对上述第一组中跨与边跨IM值求其平均，结果分别为1.20、1.14。

2.4 与各国规范的对比

各国规范对冲击系数的计算方法不尽相同，表10列出了它们在计算IM值时考虑的因素。结合文中算例桥梁，依不同国家规范计算的IM值，与取拟合分布函数下的数学期望值，在4种不同速度工况下的对比如图10所示。

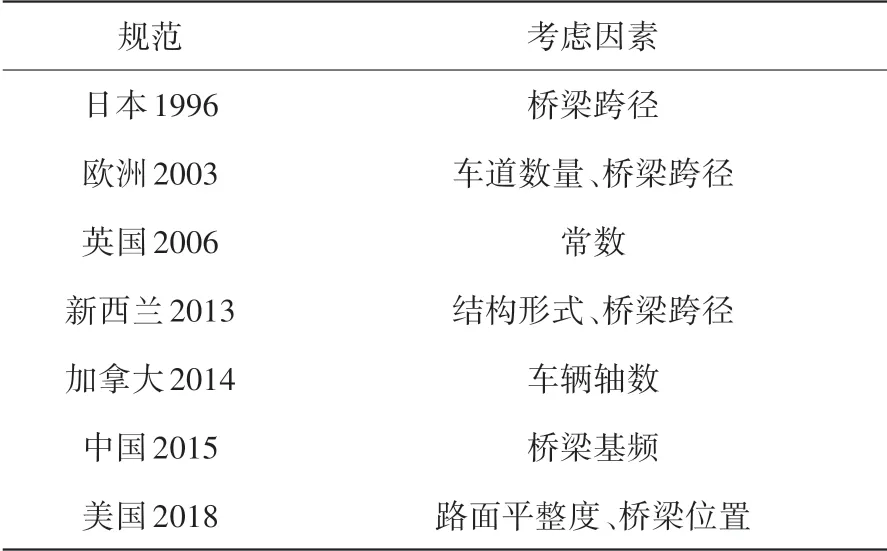
表10 各国规范计算IM值考虑因素［31］Table 10 Consider factors of calulating IM values in various coutries［31］

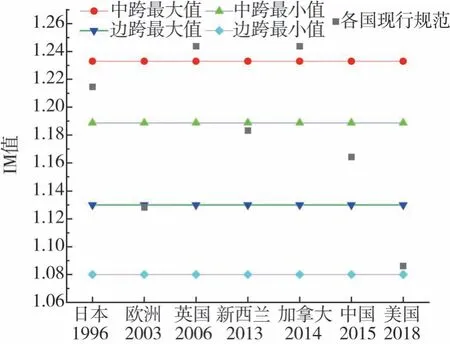
图10 文中IM值与各国规范对比Fig.10 Comparison of IM in this paper with national codes

由图10可见，英国和加拿大规范计算结果相对保守，美国规范计算结果相对偏于不安全，我国现行规范IM值计算结果为1.17，大于文中所研究桥梁的边跨IM值而小于中跨IM值，与中跨最小值相差0.01，与中跨最大值相差0.03，今后进行高速公路40 m跨径钢－混组合工字连续梁桥设计时，可考虑对桥梁中跨冲击系数适当放大。

3 结论

建立了3跨钢－混工字组合连续梁桥车－桥耦合振动分析模型，基于数值模拟与实桥静载试验、“跳车”试验和“跑车”试验实测结果的比较，验证了模型的准确性。利用车－桥耦合振动分析方法研究了钢－混工字组合连续梁桥这一国内新式桥型的动力冲击系数问题，初步获得如下认识：

（1）桥梁“跑车”试验获得中跨和边跨冲击系数值分别为1.14和1.10，而车－桥耦合数值模型计算值分别为1.18和1.13，二者具有很好的一致性（最大误差为3.38%）。

（2）桥梁中跨冲击系数近似服从正态分布，边跨冲击系数近似服从对数正态分布；中跨冲击系数略近大于边跨值。

（3）建议对40 m跨径钢－混组合工字连续梁桥设计，如按现行规范计算冲击系数应考虑对中跨取值进行适当放大。