基于混合模态数据融合的模型修正损伤识别方法

王小娟，陈峰，周宏元，2，王利辉，倪萍禾

（1.北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124；2.北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

引言

常见的工程结构，如大跨度钢桥、超高层建筑和输电塔等，极易因长时间服役、车辆撞击和酸雨侵蚀等不利因素的影响而产生损伤。结构发生损伤初期修复成本低，随着时间增加，损伤修复难度也逐渐增加，因此结构在服役期间有必要进行损伤识别及健康状况评估，以保证结构的使用安全［1］。

直接使用测量数据，如基于加速度［2－4］，位移［5］等时程曲线的时域损伤识别方法已得到广泛应用。但此类基于时域信号的方法往往要求施加特定人工激励以获取响应，难以适用于车辆荷载或环境激振等复杂激励下的结构识别问题。另一方面，频域指标如频率［6］、模态振型［7］及各类模态改进指标［8］因其抗噪性能优异，对激励形式容忍度强等优势而受到大量关注和研究。但也有研究［9－10］表明，基于单一损伤指标的频域识别方法易受结构复杂度和环境因素影响。

近年来对数据融合的研究发现，相较于仅使用单类测量数据，多类传感器测量数据融合应用于损伤识别能获得更好的识别结果，部分学者对此开展了深入研究。周俊贤等［11］从加速度与位移数据中提取模态、频响函数、静力位移，结合灵敏度分析方法将其应用于框架与板类结构的损伤识别中，其识别效果优于单一使用某种数据。Wang等［12］通过压电－光纤混合传感器网络提取结构损伤信息，用于监控航空铝板孔洞处的裂缝扩展情况，数值模拟与试验结果均表明基于融合信号的识别结果好于单一信号的识别结果。Kim等［13］将加速度－阻抗混合传感器节点用于监测结构系统，基于振动与基于阻抗的全局与局部混合监测系统成功识别螺栓松动。Wei等［14］用应变与加速度数据的简单混合证实应变模态与位移模态的互补作用，并基于两类模态对大型穹顶桁架结构进行损伤识别，取得了良好的效果。以上的研究结果表明：合理利用多类测量数据用于损伤识别比单类数据更有优势。因此，为充分利用有限数目的多类测量数据，文中推导了混合模态的计算方式，并提出基于混合模态的损伤识别方法，利用简支梁和二维框架的数值模拟验证了该方法的有效性。

1 损伤识别方法

基于模型修正的方法广泛应用于损伤识别。由于损伤会导致结构动力特性的改变，因此对结构模型动力特性的修正能反过来求解结构损伤。一般认为损伤只涉及结构刚度的改变，忽略质量变化的影响。因此，文中采用单元刚度系数变化表征单元损伤。结构整体刚度矩阵可表示为：

式中：K为结构整体刚度矩阵；αi为单元损伤因子，α=0表示单元无损伤，α=1则单元完全损伤；Θ为损伤因子向量；Ki为第i单元刚度矩阵；Nele为总单元数。

由于损伤结构模型是刚度矩阵的函数，对结构模型的修正即为求解刚度矩阵的过程。模型修正方法基本过程为：基于损伤结构模型，先对假设模型进行有限元计算或模态分析以获得识别指标，再经连续迭代过程最小化测量与计算识别指标间的差异，准确的损伤模型。因此可获得相应的刚度矩阵，损伤情况即可获取。模型修正的思想体现在连续迭代过程中，因此迭代过程的对问题的适用性和求解效率极大地影响修正的精度和速度。其中，各类优化算法因适用性广，搜索能力强，常用于结构损伤识别。

1.1 优化算法

为测试所提出识别方法对所使用算法的适用性，文中采用3种常见优化算法，分别是梯度算法、粒子群优化算法以及遗传算法，对结构进行损伤识别。

1.1.1 梯度算法

梯度算法作为一种经典优化算法，已被广泛应用于各种优化领域，此外，基于改进的梯度算法，如加速梯度、共轭梯度等的研究也取得了极为丰硕的成果。利用梯度算法求解优化问题的基本思想是将问题的负梯度方向作为搜索方向继而求出最优解。因此，梯度算法具有结构简单，迭代计算量小，占用内存少等优点。但梯度算法也存在极度依赖初始值，面对复杂问题表现不佳，易陷入局部最优等问题。

1.1.2 粒子群优化算法

粒子群优化（PSO）算法旨在模拟鸟群集体觅食时的个体特性，在接近食物时，每只鸟会根据各同伴与食物的距离调整自身位置，因此PSO对于函数的全局优化与局部优化有良好的平衡。PSO算法作为一种群智能算法，已在函数优化、机器人智能控制、工程设计等领域广泛应用。由于PSO采用速度－位移模型的全局搜索策略，利用种群内粒子的合作和竞争引导优化过程，所以优化计算时无需梯度信息，控制参数较少，易于实现且运行速度快。然而PSO在优化过程中也存在收敛精度较低、易陷入局部最优的问题，其性能也会随着待解决问题维数的增加而降低。

1.1.3 遗传算法

遗传算法（GA）是一种模拟生物进化过程的算法，通过模拟生物遗传过程中基因的重组、突变和变异，实现“优胜劣汰，适者生存”的目的，在上百次启发式搜索后得到“最优个体”。经过几十年的研究，遗传算法已经广泛应用于各领域，如函数优化，投资收益，工厂选址等。有诸如多层次遗传算法（ML－GA）［15］、微遗传算法（micro－GA）［16］等一系列基于特殊用途的改进遗传算法，能有效解决较复杂的优化问题。

1.2 协方差驱动的随机子空间法（SSI－COV）

SSI－COV法［17］是一种环境激励下基于结构离散时间状态空间方程的模态参数识别方法。假设荷载与环境作用为白噪声，则结构离散状态空间方程为：

式中：x、y、w、v分别是状态响应，监测响应，模型误差与测量误差；A为结构系统矩阵；C为结构监测位置矩阵；下标k，k+1表示离散时间步数。

系统的模态参数由上述识别的结构系统矩阵A的特征值及特征向量确定。对结构系统矩阵A进行特征分解，求解结构离散状态方程的特征值矩阵和特征向量矩阵，即：

式中：Φ为特征向量矩阵，由此可确定结构模态振型；Z为特征值矩阵：

根据离散状态方程与连续状态方程之间的关系，结构系统矩阵A的特征值与结构特征值之间有如下关系：

式中：zr，λr均为复数；上标R，I表示实部与虚部。则结构模态频率：

监测的结构模态振型为：

1.3 混合模态

模态振型作为一种局部损伤敏感识别指标，在应用中往往需要密布传感器以避免模态信息缺失而造成识别误差。但在实际工程中，特别是对于大型结构而言，密布传感器从成本上难以实现。虽然基于模态扩阶与模型缩阶的模型修正方法［18］可以解决模态不完备问题，但由此带来的误差也不可忽视。此外，大量研究［11，14，19－20］表明利用混合数据进行识别能表现出相较单类数据的优越性。因此，近年来对模态融合的研究引人关注。混合模态是依据单一模态间的关系对单一模态振型进行的拓展，获取结构混合模态首先需进行单一模态分析。由于加速度与动应变是2种较易得的响应，因此文中仅考虑对加速度与动应变2种响应的混合模态。对加速度与动应变进行传统模态分析即可获得对应的位移模态与应变模态［21］，在此基础上继续考虑两者间的关系。周计祥等［22］，陈晗等［23］给出如下应变与位移的线性变换关系：

式中：S为应变与位移的转换矩阵；ε(t)为单元应变时程。同时据式给出位移模态与应变模态的关系：

式中：S矩阵为满秩常矩阵分别为结构的第i测点位移振型向量和第i单元应变模态振型；m、n分别为总位移自由度数与总应变自由度数。考虑广义特征值问题：

式中：K、M分别为模型的刚度矩阵与质量矩阵；Ω2为特征值矩阵；位移模态Φ容易求解。在此基础上，进一步分析位移模态与应变模态的关系。结构位移和加速度频响函数分别为：

进一步地，结构的应变频响函数为：

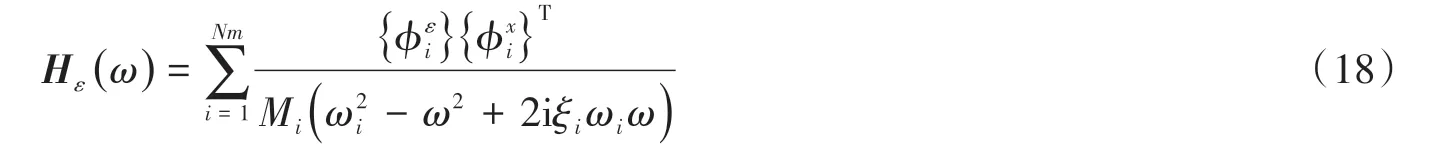
式（16）、式（17）与式（18）表明，由不同类型数据得到的频响函数仅在幅值上有较大差别，曲线峰值位置完全一致，而根据曲线幅值间的相互关系即可导出混合模态信息。因此，在结构各项参数确定时，由不同传感器获得的数据能依据模态分析方法提取出同一阶混合模态信息，该信息仅与同一阶模态频率，模态质量，阻尼比以及位移振型相关。为进一步推导不同振型信息间的相互关系，分别简化式（16）、式（17）与式（18）为：

因此，基于式（20）、式（21）建立混合模态振型，

式中：上标h,ε,x¨分别表示混合模态，应变模态及基于加速度响应获得的位移模态；I为单位阵。

文献［24］指出，对于梁式结构或框架而言，前三阶弯曲振型（排除扭转）对损伤识别效用最高，一方面，前三阶模态振型识别精度能满足损伤识别要求，另一方面，现有模态分析方法针对高阶模态的精确获取均难度较大。因此，文中所选模态阶数Nm=3，表示仅选取前三阶模态。

1.4 损伤识别算法流程

损伤识别主要流程如图1所示。首先对结构进行环境激励下的动力试验，布设加速度计与应变片测量加速度与动应变响应，利用SSI－COV对加速度和应变数据进行模态分析，即式（9）、式（10）获得结构的固有频率与混合模态振型。随后，建立结构有限元模型，将刚度损伤因子向量作为输入变量计算结构频率与位移模态以及应变模态，利用式（23）计算所假设损伤因子下模型的混合模态。进一步，将实测数据的SSI－COV模态分析结果与数值模型所计算得到的结构固有频率与混合模态输入目标函数。

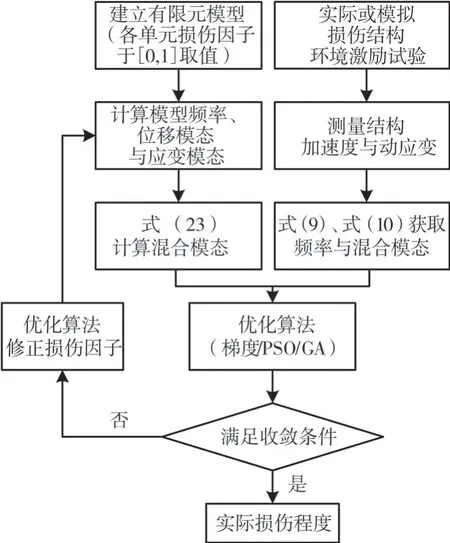
图1 损伤识别流程图Fig.1 Flow chart of damage identification

目标函数设置为：

式中：λ为相应状态模态频率，且下标mea、est分别表示测量与计算；Nm表示总模态阶数；Ns表示所有传感器数量之和，包括加速度与应变片；wf,i、wϕ,i为各项权重系数，在进行的权重系数取值测试中，目标函数中两项数值在同一数量级，两项权重系数均取1.0时识别结果表现良好。

完成目标函数的计算后，判断函数值是否满足收敛条件：若满足收敛条件则输出，根据输出损伤因子向量判断结构的损伤情况；若不满足收敛条件则修改损伤因子向量进行新一轮计算，这一过程通常采用合适的优化算法完成。为验证基于混合模态的损伤识别方法的适应性，文中将采用梯度算法、GA和PSO 3种优化算法分别进行结构损伤识别。

2 数值模拟

2.1 简支梁

为验证所提出的基于混合模态损伤识别方法的有效性，文中进行了简支梁损伤识别的数值模拟。模型具体尺寸如图2所示，梁总长1.6 m，各单元轴向长度L=0.1 m，梁高h=0.006 m，梁宽b=0.05 m。该模型包含17个节点，16个单元，共32个自由度，其中1号节点与17号节点仅允许自由转动，其他所有节点均包括平动与转动2个自由度。梁弹性模量E=210 GPa，密度ρ=7 850 kg/m3。

图2 16单元简支梁（单位：mm）Fig.2 A simply supported beam with 16 elements（Unit：mm）

结构待识别损伤参数为单元截面抗弯刚度EI的系数因子，其中I为截面惯性矩。损伤参数仅考虑单元刚度降低，单元质量于损伤前后不发生变化。在节点3、6、9、12和15施加垂直方向高斯分布的随机激励，损伤工况为单元12刚度下降50%。2种响应的时程分别为120 s，采样频率为1 024 Hz。

基于1.3节理论，对于一维等截面直梁，应变模态与位移模态关系为

式中：ui、θi、uj、θj分别是待计算应变杆件的起始和终止节点的平动与转动位移。

因此，利用式（23）和式（29）计算简支梁混合模态。在结构损伤识别中，测量数据难以避免噪声的影响，因此，在加速度与应变时程数据中加入模拟噪声：

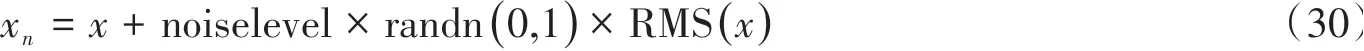
式中：x为未受噪声污染的数据；xn为相应加入噪声后的数据；noiselevel表示噪声等级；randn(0,1)表示随机生成的均值为0标准差为1的高斯分布白噪声；RMS(x)为数据的均方根。所有模拟结果均以式加入测量噪声后进行模态分析，讨论0%、10%、20%3种噪声条件下噪声对所提出识别方法的影响。

由于文中所讨论的混合模态的响应为常见的加速度与动应变响应，为验证混合模态对传统模态方法的改良，本算例共设置4种传感器布置方案，如表1所示。为讨论加速度对混合模态的贡献，设置前2种工况即工况1与工况2。前两种工况下设置有相同数量与位置的应变片，工况2增设一个加速度计，工况1未设置加速度计。为讨论动应变对混合模态的贡献，设置后两种工况即工况3与工况4。后2种工况下设置有相同数量与位置的加速度计，工况4增设一个应变片，工况3未设置应变片。

表1 简支梁传感器位置Table 1 Sensor distribution of the simply supported beam

在进行模拟之前，需进行目标函数权重系数的分析并确定其取值。由于目标函数由2项组成，分别是频率项与模态项，因此在进行权重系数取值测试时，应综合考虑频率项和模态项对目标函数的影响。一般认为，考虑权重系数的频率项和模态项数值在同一数量级时，2种动力特性的变化对目标函数有近似相同程度的影响，此时目标函数能较为有效平衡这两项分别对于识别结果的影响。

为评价频率项和模态项对目标函数收敛的影响，可将2项的收敛曲线分离出目标函数，以观察其收敛情况。选用无噪声条件下简支梁工况1使用PSO算法进行优化计算的例子作为说明，该工况下目标函数及频率项与模态项收敛图如图3所示，此时权重系数均为1.0。图3表明，随着迭代步数的增加，目标函数值逐渐降低直至收敛，同时，频率项与模态项在收敛过程中具有接近的灵敏度。图中相同迭代步数下的频率项与模态项并未选用该迭代步数下最优目标函数值所对应的两部分数值，而是随机选取该代种群中某一个体频率项与模态项的函数值，以此避免频率项与模态项受目标函数过早收敛的影响而导致其在收敛图中趋势过于平缓的问题，因此图中数值会出现相同迭代步数下频率项与模态项的函数值相加并不等于目标函数值的情形。最终频率项和模态项的收敛值分别是0.046和0.098，在同一数量级范围，因此一般性考虑下，所选2项权重系数均为1.0。在此基础上进行后续的数值模拟。

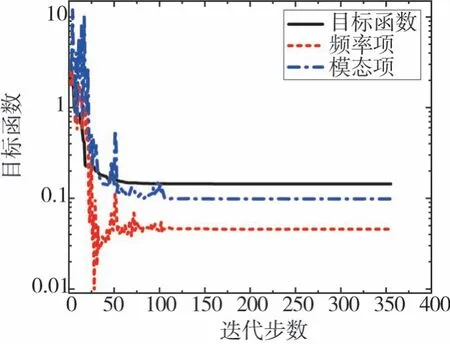
图3 简支梁工况1无噪声目标函数及频率项、模态项收敛图Fig.3 Convergence diagram of the objective function，frequency and mode terms for the simply supported beam in case 1（noise free）

由于加速度数据与应变数据的量级有差别，模拟前应先调整应变数据的单位，使计算出的混合模态的两种数据有接近的数量级。经测试，实测值中的加速度单位为m/s2，保持不变，应变单位调整为10-5ε，经上述计算的响应数据再经由模态分析方法处理，得到混合模态测量值。相应地，计算理论混合模态时，先将转换矩阵S扩大105倍，再根据式计算混合模态。4种工况下的前三阶解析振型与测量振型进行对比，并将无损结构的前三阶解析振型与测量振型也绘于图中，如图4、图5所示。图4、图5表明：经过数量级调整后的混合模态振型能很好地反映混合模态的优势，即加速度数据或应变数据可以作为额外的模态信息，包含更丰富的损伤信息，识别效果更好。

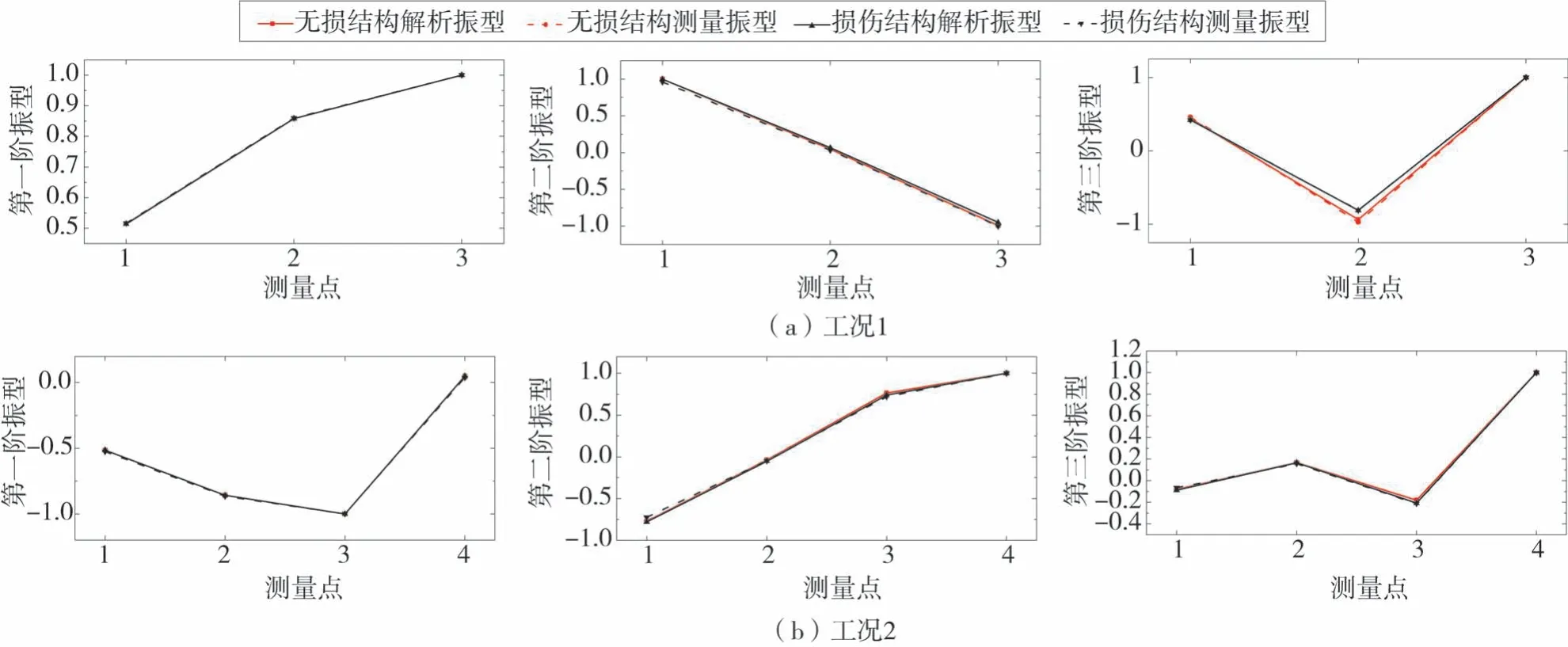
图4 解析与测量振型对比图Fig.4 The comparison charts between analytic and measured mode shape

图5 解析与测量振型对比图Fig.5 The comparison charts between analytic and measured mode shape

工况1、工况2的识别结果分别如图6、图7所示，识别误差列于表2第2行、第3行。在文中的表2、表4、表6、表7中所列出的平均误差为3种优化算法识别结果的平均值，最大误差为此3种优化算法识别结果误差最大值，误差方差统计基于3种优化算法识别结果。对比图6与图7可知，工况1无法识别出损伤的具体位置，并对损伤杆件出现严重误判，工况2尽管识别结果不理想，但对于损伤杆件有较准确的判断，因此工况2下的识别结果仍然优于工况1下的识别结果。

表6 简支梁工况5识别误差Table 6 Identification error of the simply supported beam in case 5 %

图6 简支梁工况1下应变模态识别结果Fig.6 Identification results with strain mode of the simply supported beam in case 1

图7 简支梁工况2下混合模态识别结果Fig.7 Identification results with hybrid mode of the simply supported beam in case 2

对于工况1而言，单元12损伤程度未被有效识别，其主要原因为，工况1下的传感器均为应变片，动应变是一种蕴含局部信息的损伤指标，因此在布置应变片的单元6、11、16上出现明显异于其他单元的识别结果。而工况2下仅增加一个加速度计，即表现出较强的损伤识别能力，损伤单元12的损伤程度识别结果可信。可以预见的是，随着加速度计数量的增加，识别结果将有明显改善。另一方面，工况2中布设应变片的单元6、11、16的识别结果明显好于其他未布设应变片的未损伤单元，最大误差不超过1.70%。因此，基于混合模态的识别方法中，虽然应变片对于全局损伤信息不够敏感，但其蕴含的局部信息能够极大地提高布设应变片处单元的损伤识别精度。

进一步地，工况3、工况4的识别结果分别如图8、图9所示，2种工况下的误差状况列于表2第4行、第5行。比较图8与图9可知，尽管工况3与工况4均能较好识别出损伤杆件的位置与损伤程度，但工况4的识别结果仍优于工况3。特别地，仅使用加速度信息的损伤识别方法对于简支梁的支座单元识别结果不佳。对于临近支座处的单元1与单元16而言，仅使用加速度信息的工况3的识别结果较差，而使用了加速度与应变混合模态信息的工况4的识别结果较好。工况4中在单元16处布置的应变片极大地改善了该单元的损伤识别结果，而未布置应变片的单元1的识别结果仍然不佳。因而说明混合模态中应变数据的使用对识别结果有改良作用，且改良效果主要作用于布设应变片的单元。

图8 简支梁工况3下位移模态识别结果Fig.8 Identification results with displacement mode of the simply supported beam in case 3

图9 简支梁工况4下混合模态识别结果Fig.9 Identification results with hybrid mode of the simply supported beam in case 4

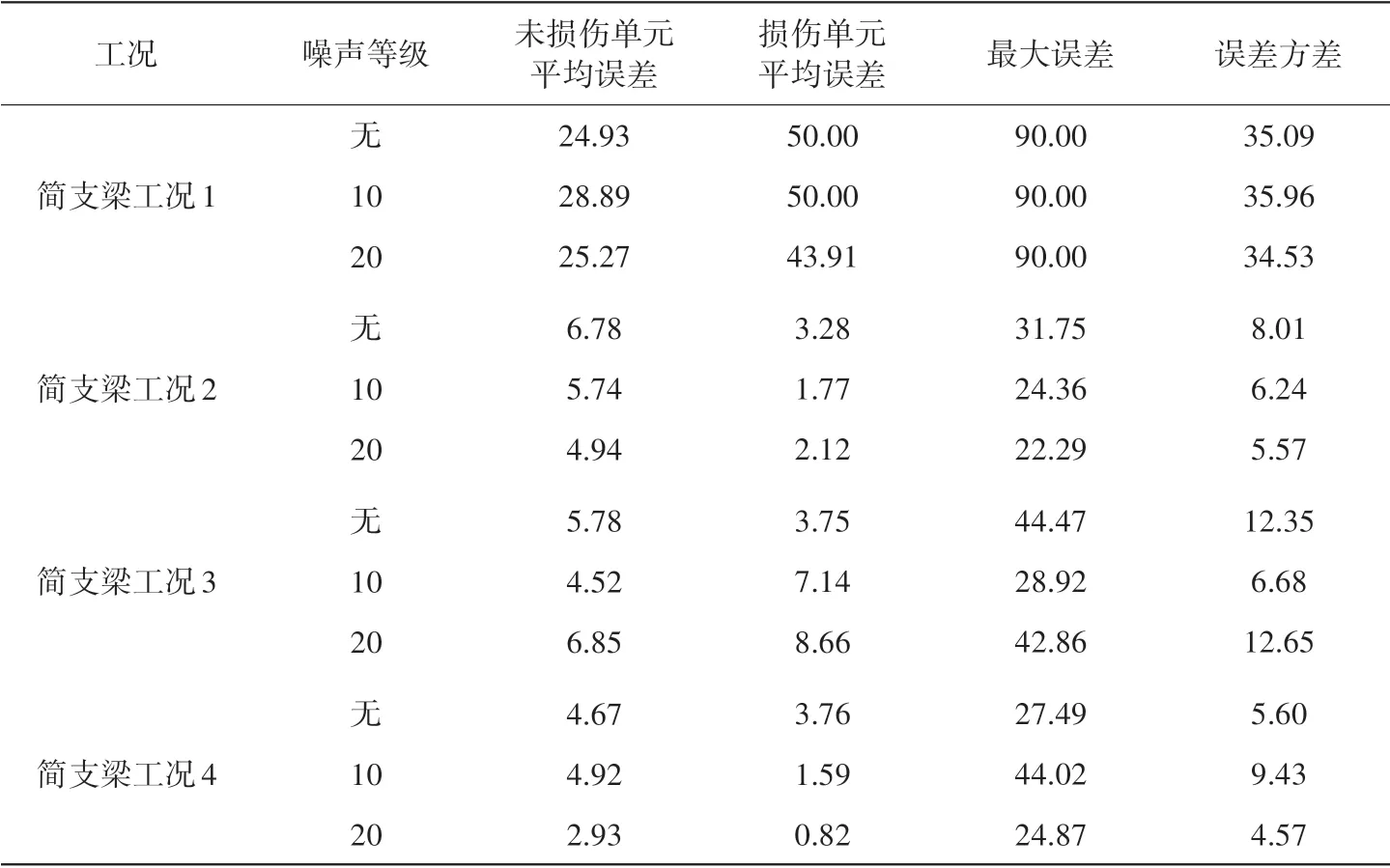
表2 简支梁损伤识别误差Table 2 Damage identification error of the simply supported beam %

由工况2、工况4识别结果可知，基于混合模态损伤识别方法在0%、10%、20%3种噪声条件下均能识别出损伤单元的具体位置，且噪声对识别结果影响较小。边界处识别结果误差大，主要原因是支座相邻单元相较其他单元模态响应小，且未在相应单元布设传感器。而引起其他单元误差的主要原因：一方面是传感器数量过少会引起模态误差，另一方面模态分析方法的识别精度不佳也会带来误差。相比于采用基于时域信号目标函数的损伤识别方法，本方法在多点未知环境激励下仍能识别出结构损伤的具体位置与损伤程度，表明本方法在未知环境激励荷载作用下的结构损伤识别中有较强的适用性。

对单一模态而言，加速度与动应变所包含的损伤信息分别是全局信息与局部信息，两者在单一模态中各自表现为：仅基于加速度模态的识别方法具有较好的全局识别能力，但对模态响应较小的边界单元的识别结果准确度不高；仅基于动应变模态的识别方法全局识别能力弱，但对于安装有应变片的单元的识别准确度高。本文所采用的混合模态同时包含加速度与动应变，由上述识别结果可知，基于混合模态的识别方法在保证全局识别能力的同时，布设有应变片的单元也有很高的损伤因子识别精度，这正是应变局部识别能力的体现。因此两种响应的优点在混合模态中均有表现，而两者缺点也相互补足，混合模态具有极高的应用性。

2.2 二维框架

采用一层一跨框架数值模拟进一步验证文中所提出损伤识别方法的有效性。框架模型包含15个单元，16个节点，每个节点包含3个自由度。共42个自由度。桁架各单元弹性模量E=210 GPa，密度ρ=7 850 kg/m3，每个单元长度为Le=0.2 m，截面积A=1.96 cm2，截面惯性矩I=0.320 1 cm4，结构形式及其他具体尺寸如图10所示。待识别参数为单元刚度的损伤因子。与2.1节简支梁数值模拟假定相同，使用单元刚度降低来模拟损伤，损伤前后杆件截面积与质量不发生变化。

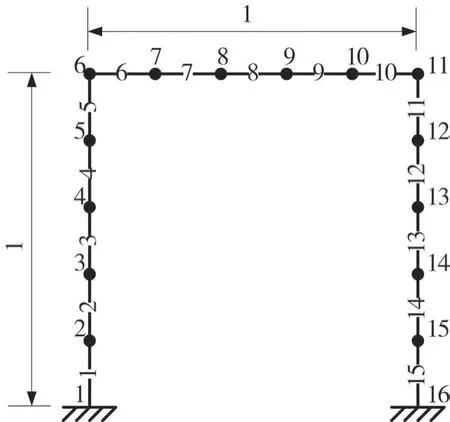
图10 15单元框架（单位：m）Fig.10 A frame with 15 elements（Unit：m）

与2.1节类似地，对于框架单元，应变模态与位移模态关系为：

则基于二维梁单元单元应变的转换矩阵为：

在6号节点沿x方向以及7号节点沿y方向对结构施加环境激励。损伤工况，传感器位置如表3所示。响应时程及采样频率与2.1节算例相同，分别为120 s，1 024 Hz。首先，同样对二维框架所有模拟测量数据基于公式加入不同程度的高斯白噪声，而后进行模态分析。在进行目标函数权重系数的取值测试后，确定框架结构的目标函数权重系数分别为wf=100，wϕ=1.0。

表3 二维框架传感器位置Table 3 Sensor distribution of the two-dimensional frame

二维框架工况1（单处损伤）的识别结果如图11所示，识别误差如表4所示。结果表明：梯度算法与GA，PSO的识别结果差别不大。尽管结构的复杂度高于2.1节简支梁，但少量传感器混合模态下的损伤识别在各噪声条件下仍对损伤有较高的敏感度。损伤单元3在20%噪声条件下平均识别误差分别为4.75%（梯度算法），9.71%（GA）与9.44%（PSO），此结果表明：基于混合模态的识别方法能较为准确地定位单处损伤杆件及识别损伤程度。

表4 二维框架识别误差Table 4 Identification error of the two-dimension frame %

图11 二维框架工况1下的识别结果Fig.11 The two-dimension frame identification results in case 1

二维框架工况2（多处损伤）的识别结果如图12所示，识别误差见表4。本方法在无噪声、10%及20%噪声条件下的最大识别误差分别为10.98%，13.54%，9.88%。识别结果表明：本方法可有效识别多处损伤位置及程度。同时，贴有应变片的单元2、8、10和12的单元损伤因子识别误差较小，3种噪声水平下的上述单元损伤因子平均识别误差仅为1.19%，1.11%，1.20%，表明混合模态中的应变数据能有效地对贴有应变片的单元做出准确的损伤程度识别。

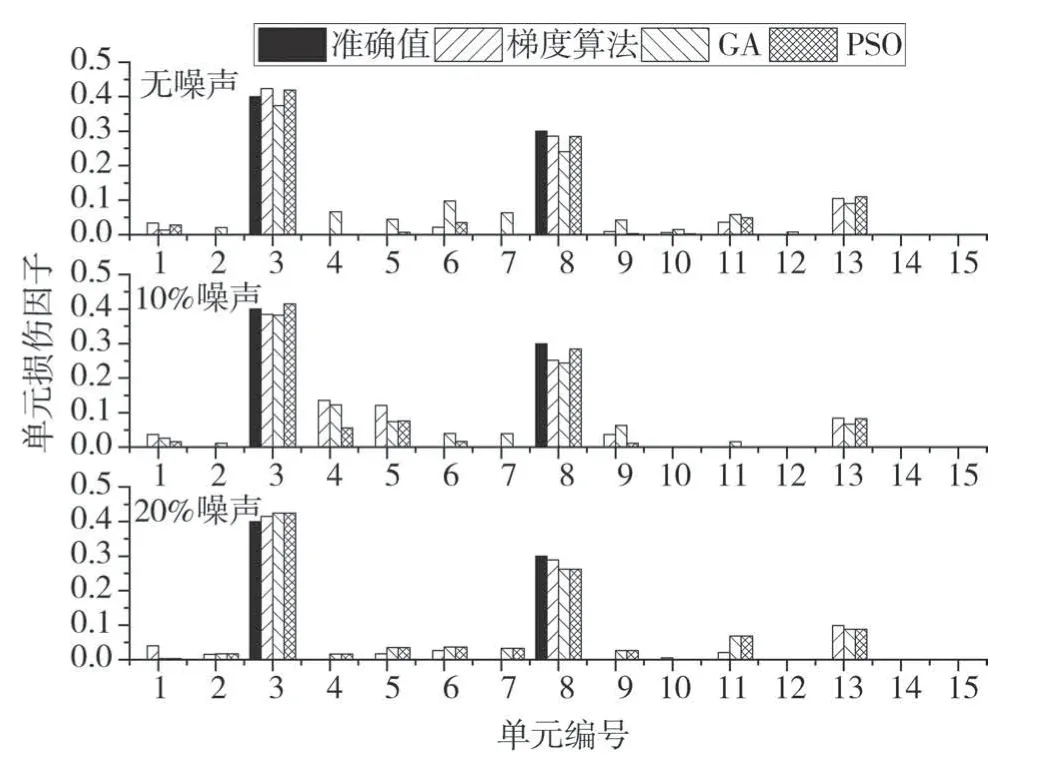
图12 二维框架工况2下的识别结果Fig.12 The two-dimension frame identification results in case 2

3 讨论

3.1 混合模态与传统方法对比分析

为验证文中所提出的混合模态的可行性，特对传感器布置方案做如下处理：该工况下2种传感器的数量均仅存在一个，即仅包含一个加速度计与一个应变片。由于仅有一种传感器类型的响应数据，在使用基于传统模态识别方法时，SSI－COV模态分析方法仅能获得频率信息而无法获取模态振型，而混合模态能同时获取其频率和模态振型信息。

将振型作为损伤指标的识别方法易受传感器数量少的影响，模态振型的测量误差将导致损伤位置和程度的识别效果较差。在基于混合模态的模型修正识别方法中，多类传感器数据的混合使用能在一定程度上缓解传感器数量少的问题，本文中的加速度与应变时程曲线在经SSI－COV方法处理后，将频率信息与混合模态同时用于损伤识别，因而其识别效果较传统方法有所改善。本节仅使用简支梁模型模拟结果，本节工况设置如表5所示。

表5 简支梁传感器位置Table 5 Sensor distribution of the simply supported beam

对工况5而言，由于加速度计与应变片均只存在一个，混合模态基于不同类型的数据仍能构建不同测点的模态振型，而传统损伤识别方法无法经由单个传感器获取不同测点的振型相互关系，因此仅能获得固有频率信息作为损伤识别指标，目标函数式转化为：

图13与图14分别是基于混合模态与传统仅基于频率在不同噪声条件下的损伤识别结果，平均识别误差如表6所示。一方面，由图13和图14的识别结果可知，噪声等级对识别结果精度影响不大，随着噪声等级的增加，识别结果基本一致。由于传统方法的目标函数仅与结构的频率有关，混合模态的目标函数同时包含结构的频率与模态振型，而低阶频率和振型受噪声的影响小，因此两者的识别结果均表现出对噪声的不敏感。

图13 简支梁工况5下混合模态识别结果Fig.13 Identification results with hybrid mode of the simply supported beam in case 5

图14 简支梁工况5下传统方法识别结果Fig.14 Identification results with the conventional method of the simply supported beam in case 5

另一方面，比较图13与图14的识别结果可知，图13的识别结果优于图14。特别地，对于损伤杆件12的识别中，混合模态与传统方法下的3种智能算法下的平均识别误差为6.00%与35.98%，而其他未损伤单元的平均误差分别为5.88%与8.36%。这一结果说明，仅有一个加速度计与一个应变片的条件下，传统仅基于频率方法的识别难以判断损伤位置，而基于混合模态的识别能够判断出损伤的位置，且识别精度较传统方法有较大提高。

3.2 损伤程度

为确定基于混合模态损伤识别方法在小损伤情况下的表现，本节将简支梁损伤单元12刚度分别退化20%、30%、40%后进行损伤识别，传感器布置情况与简支梁工况4一致，识别结果如图15、图16、图17所示，识别误差情况如表7所示。

表7 简支梁不同损伤程度识别误差Table 7 Identification error of the simply supported beam with different degrees of damage %

图17 简支梁工况4单元12损伤程度为40%的识别结果Fig.17 Identification results of the simple-supported beam in case 4（unit 12 with 40%damage degree）

图15表明，在损伤程度仅有20%情况下，本方法3种噪声等级下均难以有效识别损伤的具体位置，其主要原因是传感器数量较少且本方法所采用的识别指标为频率与前三阶位移、应变模态振型构成的混合模态，指标对损伤程度的敏感性有限，因此本方法对较小程度的损伤难以准确识别。随着损伤程度的增加，损伤单元的平均误差由19.2%（20%损伤），降低至5.14%（30%损伤），最后至2.22%（40%损伤），损伤识别精度逐渐增加。图16表明，在单元12损伤程度为30%时，尽管损伤单元的损伤程度并未被准确识别，但在不同噪声条件下，本方法的识别效果接近，本方法具有较强的噪声鲁棒性。

图15 简支梁工况4单元12损伤程度为20%的识别结果Fig.15 Identification results of the simple-supported beam in case 4（unit 12 with 20%damage degree）

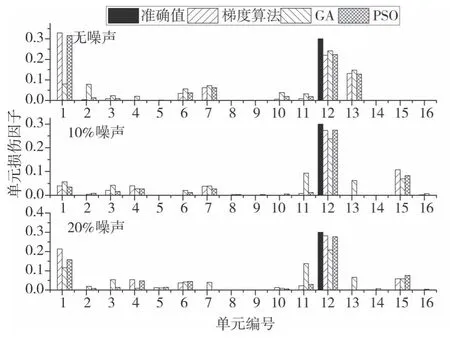
图16 简支梁工况4单元12损伤程度为30%的识别结果Fig.16 Identification results of the simple-supported beam in case 4（unit 12 with 30%damage degree）

4 结论

文中建立了位移模态与应变模态的内在联系，并提出了混合模态的概念，证明了使用混合模态用于损伤识别的可行性。进一步将混合模态应用于模型修正方法中，结合3种优化算法进行损伤识别，并得出以下结论：

（1）加速度与动应变混合模态提供了不同数据类型模态间的相互关系，其中，加速度与动应变同阶信息间的相互关系仅与该阶模态频率有关。

（2）混合模态更能充分有效利用不同测量数据提取模态振型，基于混合模态的损伤识别结果较单一模态有改进，其中，加速度响应提高方法的全局识别效果，而应变响应对装有应变片单元的识别效果有明显改善；

（3）本方法在3种智能算法及3种噪声条件下的识别结果相近，说明混合模态对噪声的鲁棒性强，对智能算法适应能力强。

由于本方法仅仅使用了前三阶模态信息，因此存在一定的识别误差，但文中着重对比本方法与传统方法的识别效果，因而在模拟中保持使用相同工况下同等传感器布置方案，只注重对2种方案结果的对比，模拟结果符合预期。因此本方法有其局限性，但可通过以下2方面工作改善：一方面，由于高阶模态信息拥有对损伤信息的更高的敏感性，因此可选择更多阶模态信息以求改善识别效果。另一方面，由于模态振型信息同时包含有结构的空间信息，因此，增加传感器数量能有效地增加本文所提出混合模态指标的识别效果。