高质量发展视角下长江经济带物流效率测度研究

梁雯 殷伟伟

(安徽大学 商学院，安徽 合肥 230039)

一、引言

物流业是国民经济发展的重要动脉，是国民经济中的基础性产业，不但对国民经济发展具有重要意义,同时也在调整产业结构、优化资源配置、提升区域竞争力等方面发挥着重要影响。近年来，中国各地区政府都在新一轮行业规划调整中将物流业作为重要行业优先发展，将物流业高质量发展作为重要着力点。2019年国家发改委、交通运输部等24个部门联合发布了《关于推动物流高质量发展促进形成强大国内市场的意见》，2020年国家发改委推出了《关于进一步降低物流成本的实施意见》《“十四五”现代流通体系建设规划》,提出在双循环背景下构建更加完善的物流体系，突破物流低效率的瓶颈，促进经济循环[1]。

长江经济带是最具影响力的流域经济带之一，长江经济带高质量发展对带动中国整体经济高质量发展具有重大的意义[2]。在中国经济高质量发展的背景下，物流业扮演着必不可少的角色，因此对长江经济带物流效率的研究具有重要的现实意义。基于此，本文基于长江经济带2011～2020年11个省市的数据，运用三阶段DEA模型、Tobit计量经济模型和Malquist模型对物流效率进行研究。

二、国内外文献综述

国外学者主要从国家层面和企业层面对物流效率进行研究。一是基于国家层面。Markovits-Somogyi等(2014)利用DEA-PC与DEA方法对比分析了欧洲29国的物流效率[3]。在物流效率评价中，国家之间的基础设施建设对于物流效率也具有一定的影响，这在Saparovna Mukhtarova等(2018)的研究中得到了证实[4]。 二是基于企业层面。Tae Hoon Oum等(2013)通过研究日本运输企业发现铁路公司效率高于航空公司效率[5]。Sung Hoon Park等(2018)分析了韩国沿海轮渡企业效率[6]。Wong等(2015)分析了新加坡和马来西亚物流公司的效率，发现企业大小对物流效率也具有影响[7]，因此不仅需要关注整个物流行业的情况，企业内部管理也具有举足轻重的作用。Lakshmi Pothuraju Vijaya等(2019)的研究发现员工缺勤会对企业物流效率造成影响[8]。

国内学者主要从以下两个角度对物流效率进行研究：(1)从理论角度出发。何黎明(2018)认为物流供需结构升级、新旧动能转化、基础设施网络化等能够推进物流高质量发展[9]。物流高质量发展离不开物流体系运转效率的提升，粟晨静(2019)提出要在政府、信息技术和人员专业素质三个方面进行提升，以更好地服务于物流体系[10]。丁海宁等(2016)认为可以从物流基础设施、信息服务平台、物流网络布局、多部门合作、航空物流五个方面入手提升物流效率[11]。另外，季小立(2018)、李翠芝(2020)都认为物流企业创新可以提高其效率，增强竞争力[12,13]。(2)从实证角度出发。一部分学者采用单一DEA模型进行研究，张璇等(2016)、王书灵等(2016)、王博等(2019)、汪文生等(2021)、龚瑞风等(2022)运用三阶段DEA模型对新丝绸之路经济带、江浙沪地区、“一带一路”沿线地区、环渤海地区、全国31个省市的物流效率进行测算[14～18]。另一部分学者将DEA模型与其他模型相结合进行分析，于丽英等(2018)采用了DEA和Malmquist指数模型，认为从资源整合、技术创新和协同合作等方面可提升物流效率[19]；龚雅玲等(2019)采用DEA和Tobit模型进行研究，认为物流效率受到产业结构、信息化和产业发展优势三个方面的影响[20]；张云宁等(2020)利用DEA、Tobit和Malmquist模型对中国长江大保护地区的物流效率进行研究[21]；曹炳汝等(2019)利用DEA模型、ArcGIS和空间自相关分析方法进行研究，认为提升物流效率的策略包括产业转型升级、区域间协调合作、加强对外开放等[22]。

综上所述，尽管关于物流效率的研究成果丰硕，但仍然有不足之处：一是现有研究对象主要集中在国家或单个省域，鲜有以长江经济带作为分析对象；二是大部分学者采用DEA模型对物流效率进行测算，忽视了环境、随机误差和管理因素的影响；三是大多数研究只采用单一的研究方法，所以对物流效率的研究不够深入。基于此，本文首先利用三阶段DEA模型对长江经济带物流效率进行测度，然后利用Tobit模型分析外部环境因素对物流效率的影响，最后利用Malquist模型对物流效率进行动态研究。

三、研究方法与数据来源

(一)三阶段DEA模型

三阶段DEA模型最早来源于Fried等人[23]对DEA模型的延伸。具体计算步骤如下：

1.DEA-BBC模型

本文利用规模报酬可变的情况下投入导向的BBC模型，公式如下：

(1)

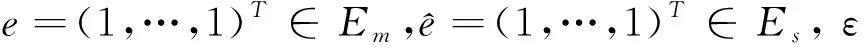
2.相似SFA模型

这一阶段的目的是剔除环境效应、随机干扰和管理无效率对物流效率的影响。具体步骤如下：

(1)建立SFA回归方程：

Sni=f(Zi;βn)+νni+μni

(2)

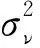
(2)采用罗登跃(2012)的方法[24]进行管理无效率分离和计算随机误差项：

(3)

E[νni|νni+μni]=Sni-f(Zi;βn)

-E[μni|νni+μni]

(4)

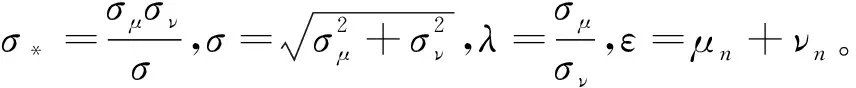
(3)对投入变量进行调整：

+[max(νni)-νni]

(5)

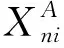
3.调整后的DEA-BBC模型

根据第二阶段新的投入量再次运用DEA-BBC模型进行测算，这一阶段所得出的结果更加真实可靠。

(二)Tobit模型

因为DEA-BBC模型所得效率值范围为0～1，所以普通最小二乘回归方法对本文不适用，因此本文采用Tobit回归模型以减少误差[25]，模型如下：

Y=β0+β1X1+β2X2+β3X3+β4X4+ε

(6)

其中Y为被解释变量，X为解释变量,β0为常数项，ε为误差项。

(三)Malmquist指数模型

Malmquist指数模型最早由Malmquist在1953年提出，后来Caves用于生产率指数[26]，具体公式如下：

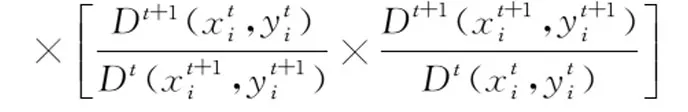
=EC×TC

(7)

其中x、y分别表示投入和产出；D(x,y)表示距离函数；EC表示技术效率，TC表示技术进步。

(四)指标选取与数据来源

1.投入、产出指标与环境变量的选取

在参考以往学者研究[14,27]的基础上，本文从物力、人力、资本三个角度选取投入和产出指标。在环境变量上要选取那些对物流效率产生影响但不受物流业主观控制的变量,本文主要选取地区生产总值、政府支持度、社会消费品零售总额三个指标。具体评价指标体系见表1。

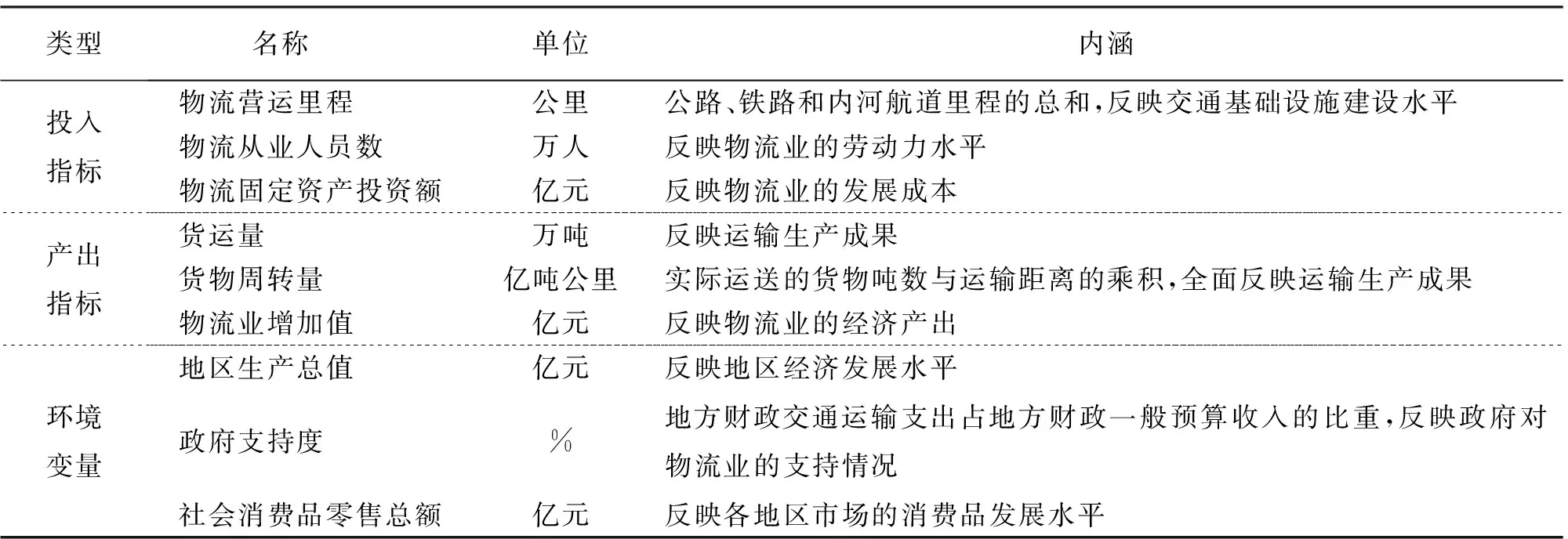
表1 物流效率评价指标体系

2.数据来源

本文选取长江经济带11省市2011～2020年的数据，数据来源于《中国统计年鉴》、历年分省(市)统计年鉴、中经网统计数据库网站和国家统计局网站。我国目前没有单独评价物流业的数据,所以部分物流业的数据由交通运输、仓储及邮电业的数据代替[28]。

四、实证分析

(一)第一阶段传统的DEA实证结果分析

根据投入产出数据，利用Deap2.1软件测算得出长江经济带2011～2020年间各省(市)物流业综合技术效率、纯技术效率和规模效率，具体见表2～表4所示。

表2 长江经济带物流综合技术效率

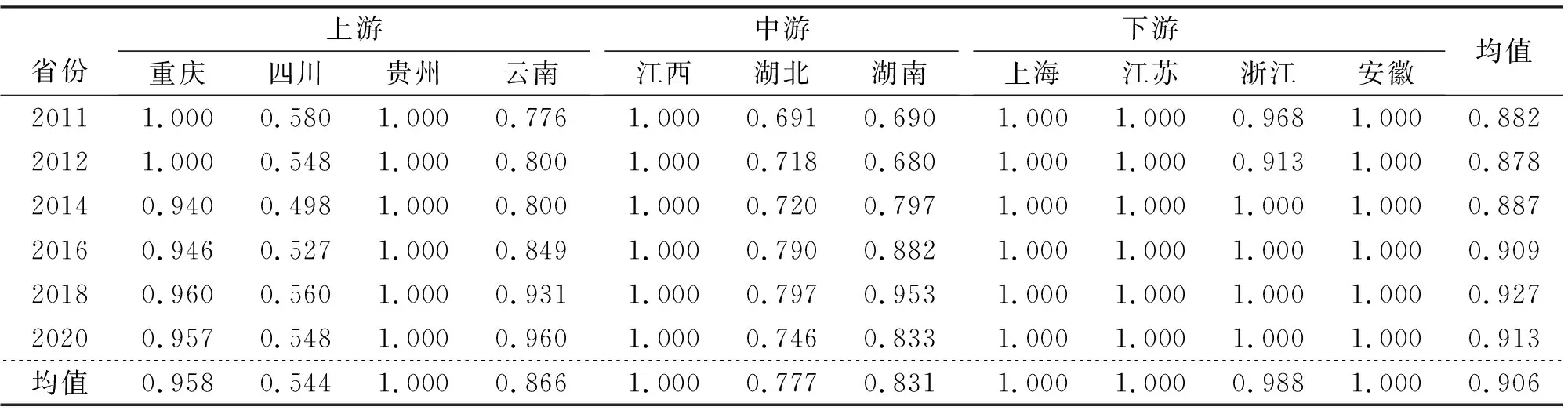
表3 长江经济带物流纯技术效率

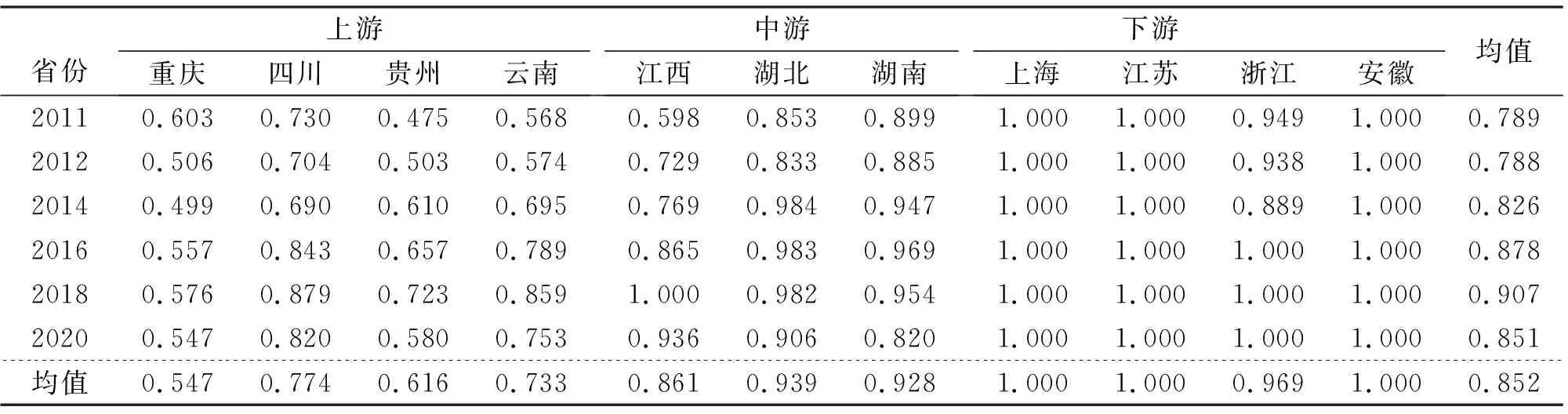
表4 长江经济带物流规模效率

从综合技术效率来看,下游地区>中游地区>上游地区,这就意味着下游地区的物流输出能力较强,资源得到了充分发挥。这是因为近年来,我国政府对长三角地区物流业发展的关注程度较大,并制定了《长江三角洲区域一体化发展规划纲要》,让长三角区域成为领头区域，引导其他地方物流业朝着更高效的方向发展。而上游地区效益相对较差的主要原因可能在于其区域地形比较复杂,在交通方面处于劣势地位。

从纯技术效率来看，贵州、江西、上海、江苏、安徽都达到了1，说明这5个地区对投入因素的利用率已经达到了最高水平；重庆市在2011和2012这两年达到了技术效率前沿面，随后呈现下降的趋势，但是整体上仍处于较高水平；浙江省则与重庆市相反，在2011、2012年虽然没有达到技术效率前沿面，但从2013年起其技术效率一直为1。11个地区中四川省的技术效率最低，说明其投入并没有得到很好的产出，物流管理水平较低。

从规模效率来看，上海、江苏、浙江均为1，且浙江>湖北>湖南>江西>四川>云南>贵州>重庆。除了上海、江苏和浙江这三个省(市)的规模效率一直保持为1之外，其他省(市)的规模效率都呈现反复变化的趋势，说明其他省(市)还存在上升空间。

综合来看，上海、江苏、安徽这三个地区每年度的综合技术效率、纯技术效率和规模效率数值均为1,而长江经济带综合技术效率、纯技术效率和规模效率数值整体大致呈上升态势,表明物流发展水平在逐渐提高，但还存在进步的空间。其中，从长江经济带总体上看，纯技术效率对综合技术效率的贡献比规模效率大。

(二)第二阶段SFA回归结果分析

SFA回归模型中被解释变量为第一阶段所求得的物流营运里程、物流从业人员数和物流固定资产投资额这三者的松弛变量，解释变量为地区生产总值、政府支持度和社会消费品零售总额，利用Frionter4.1软件对2011～2020年长江经济带的数据进行分析，结果见表5。

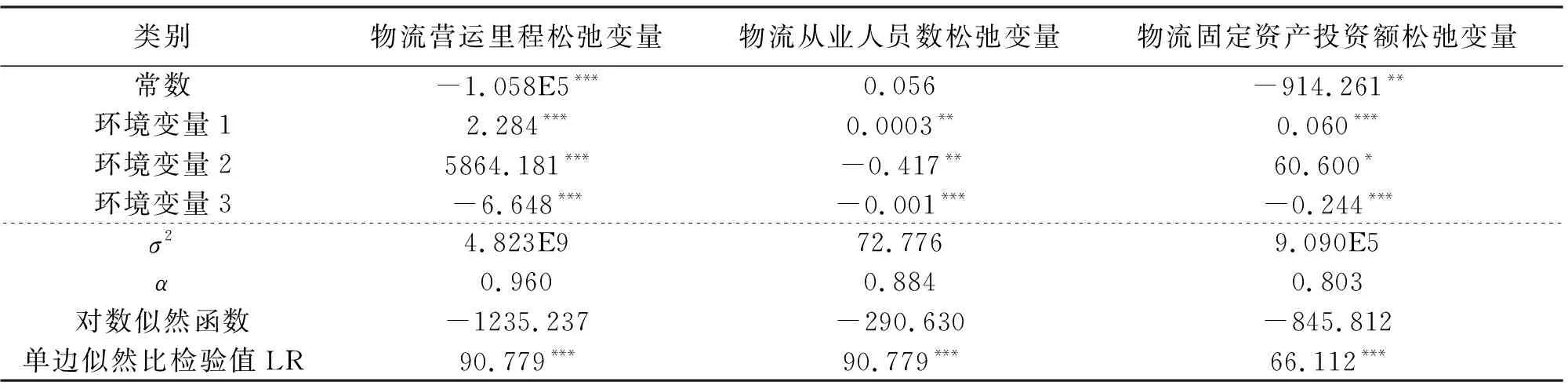
表5 SFA回归模型汇总结果

由表5可知，所选取的3个环境变量的单边似然比检验结果都通过了1%的显著性检验，说明环境变量对物流的投入松弛变量都有较大影响力,具体分析如下。

1.地区生产总值

此环境变量对3个投入松弛变量的回归系数均为正数但是值较小，表明地区生产总值的增加会带来物流营运里程、物流从业人员数、物流固定资产投资额这三者的松弛变量的增长，进而对物流效率产生消极作用。GDP的增长可能会引起物流业进行盲目投资并吸引更多的人员进入物流业，从而导致物流效率的下降，因此要合理分配资源，实现资源最大化利用。

2.政府支持度

此环境变量对物流营运里程和物流固定资产投资额这两者松弛变量的回归系数为正数，对物流从业人员数松弛变量的回归系数为负数，表明政府对物流基础设施和固定资产投资过多从而导致浪费，而对于物流从业人员数，政府的控制能力较好，可以防止过多人员从事物流业从而造成人员的冗余。

3.社会消费品零售总额

此环境变量对3个投入松弛变量的回归系数均为负数，表明社会消费品零售总额的增加会带来物流营运里程、物流从业人员数、物流固定资产投资额这三者的松弛变量的降低，因而对物流效率具有积极作用。市场交易额的增加带动了物流效率的提升，是物流业发展必不可少的基石。

(三)第三阶段投入调整后的DEA实证结果分析

根据第二阶段新的投入数据，再次利用DEA-BBC模型进行测算，可以看出与第一阶段相比数值发生了变化，说明随机因素和环境因素对物流效率具有一定的影响力，具体见表6～表8所示。

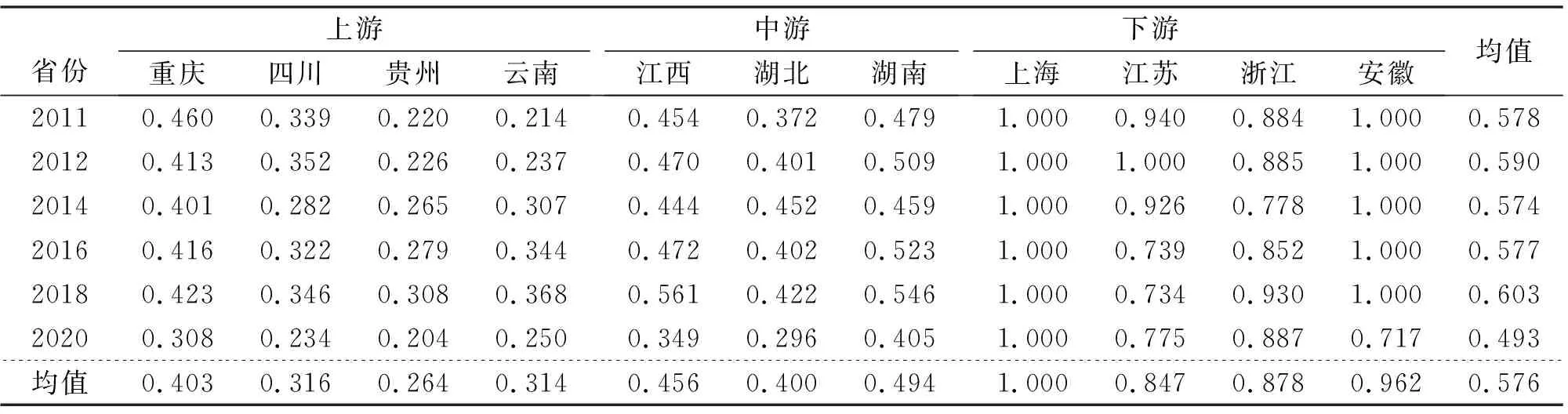
表6 投入变量调整后的长江经济带物流综合技术效率

表7 投入变量调整后的长江经济带物流纯技术效率

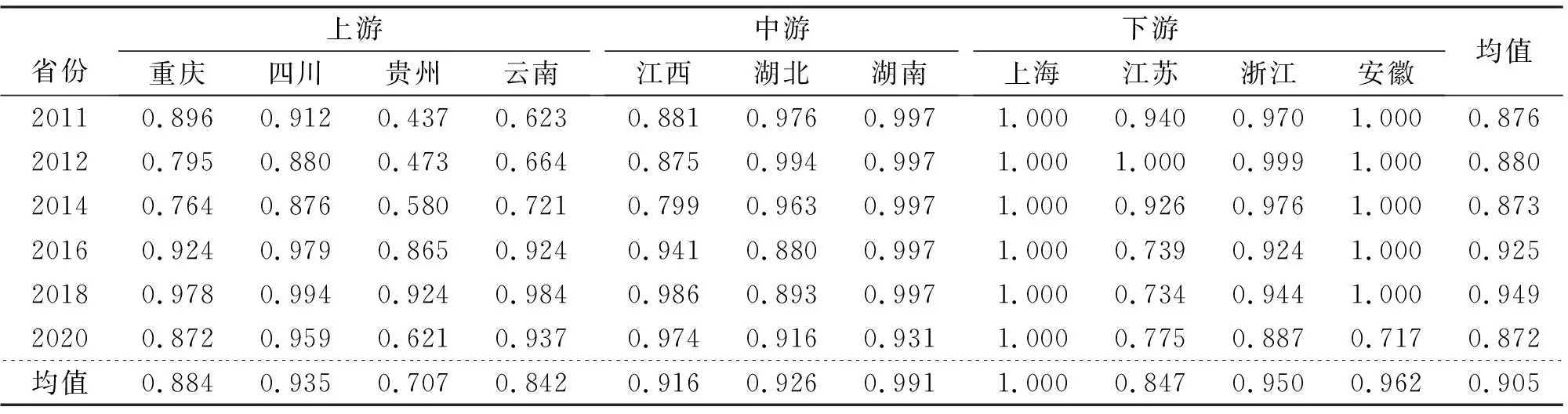
表8 投入变量调整后的长江经济带物流规模效率

1.从时间角度分析

长江经济带各省(市)每年的物流综合技术效率和纯技术效率值都小于第一阶段，而规模效率值都大于第一阶段，说明纯技术效率在物流效率中起作用的程度更大。具体改进措施可从两方面入手：第一，各省(市)政府应出台支持技术创新的政策，以实现高质量发展；第二,各省(市)企业和学校也应加强对技术人员的培养，例如开设学习新技术的课程。

2.从空间角度分析

(1)将第一阶段和第三阶段的综合技术效率进行对比，除了上海，其他10个省(市)的效率都下降了，其中贵州省下降程度最大，为57.15%，说明其受环境影响的程度最大。从表6可以看出，下游地区受环境影响程度最小。(2)对比第一阶段和第三阶段的纯技术效率，上游地区效率下降程度大于中游地区，而下游地区中上海、江苏和浙江效率没有变化且已达到效率最前沿面，并始终保持着纯技术效率为1，下游中只有浙江纯技术效率下降了6.43%。(3)对比第一阶段和第三阶段的规模效率，上海依旧没有变化，规模效率值为1，其他省(市)虽然没有达到DEA有效，但是规模效率也比较高。四川、江西、湖北、湖南、浙江和安徽的规模效率值在0.9～1之间，重庆、云南和江苏的规模效率值在0.8～0.9之间，只有贵州的规模效率值0.707为最低。湖北、江苏、浙江和安徽都有不同程度的下降，江苏的下降程度最大，为15.35%，而其他省(市)规模效率都是提高的，其中重庆市的提升幅度最大，为61.49%。

总的来看，只有上海调整前后的三种效率值都无变化并都为1，说明上海的资源得到了高效利用，并且达到了最大产出，而其他省(市)都需要重点提高物流的纯技术效率以进行优化。从长江经济带总体上看，规模效率对综合技术效率的贡献比纯技术效率大。

(四)长江经济带物流效率影响因素分析

影响物流效率的因素是复杂多样的，三阶段DEA所得出的物流效率可能不够完善。为了深入研究影响物流效率的因素，本文进一步构建Tobit回归模型进行分析，其中被解释变量为长江经济带物流效率，解释变量包括：外贸水平，用进出口总额(千亿美元)衡量；信息技术水平，用互联网宽带接入端口数(千万个)衡量；物流产业结构，用地区物流业产值占总产值的比重(%)衡量；区位商，用地区物流业产值占总产值比重/全国物流业产值占总产值比重的比值(%)衡量。结果见表9。

由表9可知，外贸水平和物流产业结构在1%的水平上显著且系数为正，外贸水平系数值比物流产业结构系数值小，说明外贸水平对物流效率的正向影响比物流产业结构对物流效率的正向影响小；信息技术水平在5%的水平上显著且系数值为-0.013，说明其对物流效率具有负面影响但影响力比较小；区位商在1%的水平上显著且系数值为-1.300，说明区位商对物流效率具有负面影响且影响较大，可能因为长江经济带上游地区(如重庆、四川等)地势较为复杂且以山地、丘陵为主，这对物流运输方面会造成一定的阻碍，从而降低物流效率。

表9 Tobit回归结果

(五)长江经济带物流效率动态分析

根据第三阶段DEA所得的投入产出数据构建Malmquist模型,进一步分析长江经济带物流效率动态发展趋势,具体结果见表10和表11。

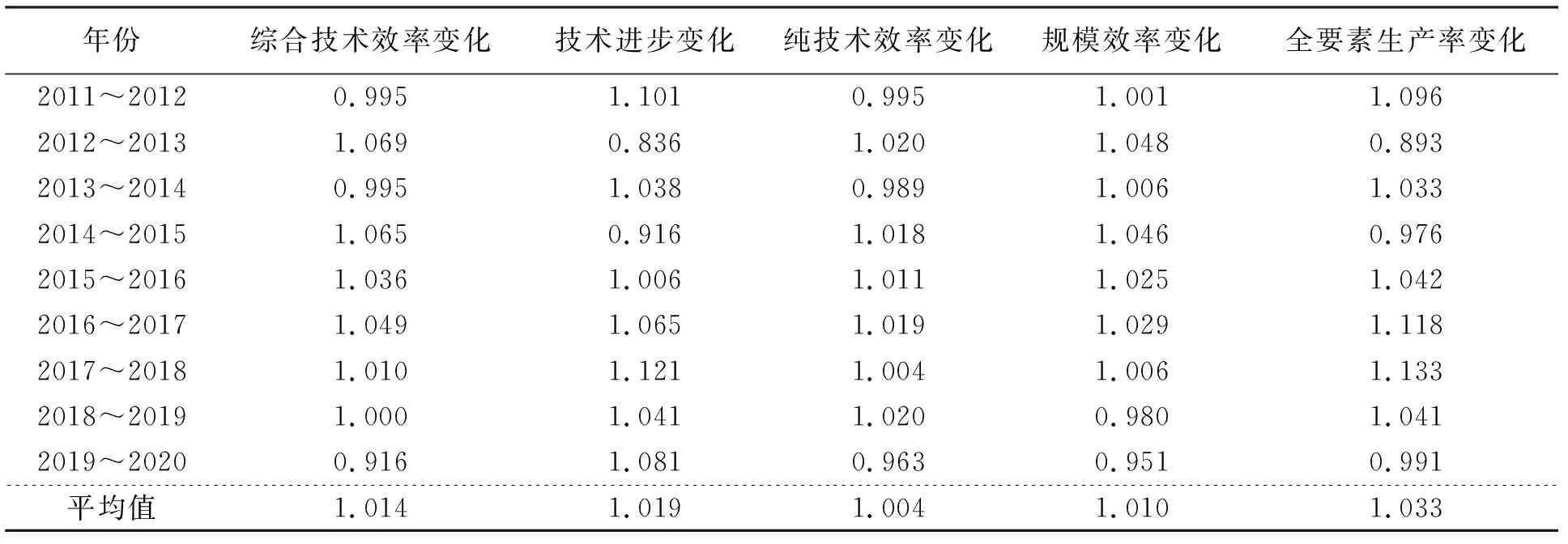
表10 长江经济带2011～2020年物流业Malmquist指数的变动与分解

从表10可知，整体上物流效率都是提高的，物流的全要素生产率上升了3.3%，主要来源于两方面：一方面得益于综合技术效率上升了1.4%,另一方面得益于技术进步上升了1.9%，对比这两个数值就可以发现全要素生产率变化主要依赖于技术进步的提高。综合技术效率的上升也包括两个方面：一方面是得益于纯技术效率上升了0.4%，另一方面是得益于规模效率上升了1%，由此可知规模效率的上升是带动综合技术效率上升的主要因素。

2011～2020这10年间长江经济带的物流效率波动较大。物流全要素生产率除了2012、2014、2019年下降外，其余年份都大于1，其中2012年降低幅度最大，2016年提高幅度最大，达到11.8%，贡献程度最大的是技术进步，提高了6.5%。

从表11可知，除了重庆、江苏和安徽的全要素生产率呈下降趋势，分别下降了0.1%、0.2%和2.9%外，其他8个省(市)都呈上升趋势。其中，下降程度最大的为安徽省，技术落后是主要原因，因此安徽省应该注重提高物流业的智能化水平。提升程度最大的为云南省，数值为10.6%，其中综合技术效率贡献了5.7%，技术进步贡献了4.7%，由这两个数值可以发现技术进步和综合技术效率对云南省全要素生产率的贡献都具有积极的影响。

分区域来看，全要素生产率排名第一为上游地区，第二为中游地区，下游地区最小。其中上游地区全要素生产率上升了6.4%，综合技术效率上升了1.8%，技术进步上升了4.6%，纯技术效率上升了0.3%，规模效率上升了1.4%，全要素生产率上升主要得益于技术进步；中游地区全要素生产率上升了2.9%，综合技术效率上升了2.6%，技术进步上升了0.3%，纯技术效率上升了1.0%，规模效率上升了1.6%，全要素生产率上升主要得益于综合技术效率提高；下游地区全要素生产率上升了0.9%，综合技术效率上升了0.3%，技术进步上升了0.6%，纯技术效率上升了0.1%，规模效率上升了0.2%，全要素生产率上升主要得益于技术进步但带动作用不明显。

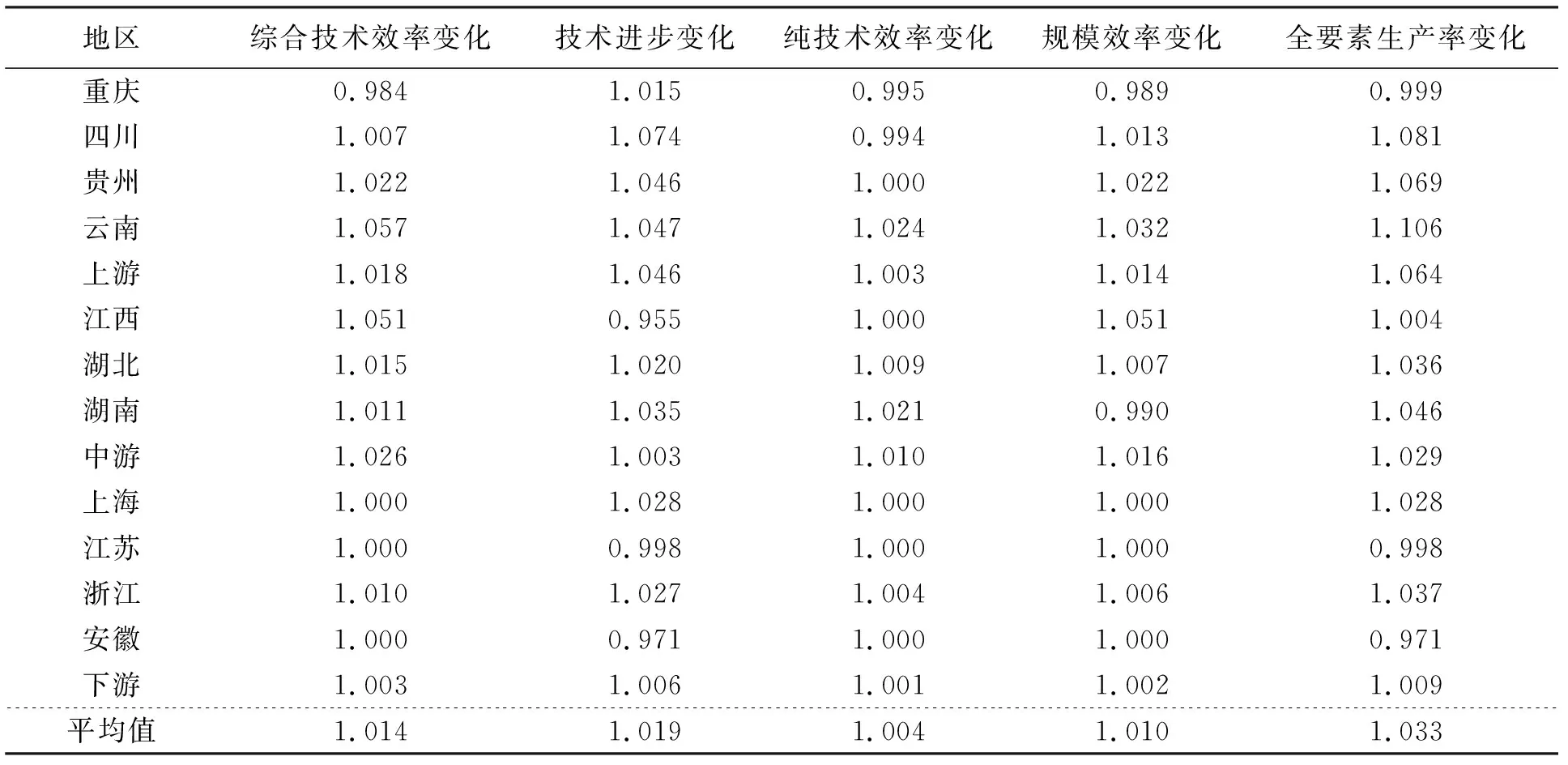
表11 长江经济带2011～2020年各省市物流业Malmquist指数的变动与分解

五、研究结论与政策启示

(一)研究结论

本文基于长江经济带11个省(市)2011～2020年的数据，利用三阶段DEA、Tobit和Malmquist模型研究长江经济带的物流效率，研究发现：(1)调整前物流综合技术效率依次递减的排序为上海、江苏、安徽、浙江、江西、湖南、湖北、云南、贵州、重庆、四川。其中上海、江苏、安徽并列第一，并且都已达到效率前沿，但是长江经济带总体综合技术效率不高。调整后的物流综合技术效率依次递减的排序为上海、安徽、浙江、江苏、湖南、江西、重庆、湖北、四川、云南、贵州，其中只有上海达到效率前沿，长江经济带总体综合技术效率比调整前更低且规模效率高于技术效率，长江经济带物流效率提高的关键在于规模效率提升。(2)外部环境对物流效率具有显著影响。长江经济带外贸水平与物流产业结构对物流效率具有正向作用，其中物流产业结构对物流效率的作用程度大于外贸水平对物流效率的作用程度；信息技术水平与区位商对物流效率具有负向作用，其中区位商对物流效率的作用程度大于信息技术水平对物流效率的作用程度。(3)长江经济带过去10年全要素生产率平均上升了3.3%，综合技术效率上升了1.4%，技术进步上升了1.9%，技术进步是影响全要素生产率的关键因素。其中只有重庆、江苏和安徽的全要素生产率降低，因此要加大这三个地区物流产业结构化力度。

(二)政策启示

基于上述结论，本文提出以下政策启示：(1)重视全局平衡性。大力促进区域间合作，缩小发展差距，长江经济带各省(市)应加强交流合作，形成产业间的协同发展。(2)加强对外开放程度。长江经济带区域具有先天地理优势，港口物流是长江经济带物流的引擎，也是对外开放的关口，因此要利用好这一优势，提高物流的外向度。(3)改善管理方式，提高规模效率。企业和政府应加强合作，优化空间布局，使得资源和企业更加集聚化，从而提高资源利用率。(4)促进产业结构升级，推动产业结构向合理化、高级化方向发展。(5)提升物流技术水平和技术效率，以减少企业运营成本，提升企业活力。