高动态环境二进制偏移载波调制信号的捕获

方竹 张天骐 汪锐 王雪怡

（重庆邮电大学通信与信息工程学院，重庆 400065）

1 引言

全球卫星导航系统（GNSS，Global Navigation Satellite System）是当前发展速度最快、应用广泛的信息技术之一。无论是导航、测量、军事、还是城市管理都离不开GNSS 系统。如何在有限的频谱内实现精确的捕获成为GNSS 的研究热点。接收信号往往在两万公里以外，而且信号在穿过建筑物、隧道等障碍物时，甚至在遇到下雨天气时都会衰减。实际的通信环境又非常复杂，飞行器速度非常快、甚至有加速度和加加速度的产生，所以接收到的信号往往具有大多普勒频偏甚至一阶多普勒变化率。因此，接收机接收到的大多数是含噪声的动态信号。

目前，对于二进制偏移载波调制信号（BOC，Binary offset carrier）大多数捕获算法都是在没有多普勒频率变化率的前提下使用，不能对高动态运动引起的一阶多普勒变化率进行有效补偿。为了捕获到高动态环境下的BOC 信号，文献［1-3］提出了使用部分匹配滤波器结合快速傅里叶变换（PMFFFT，Partially Matched Filter -Fast Fourier transform）的捕获算法，提高了多普勒频偏的分辨率，但仍无法补偿多普勒变化率。文献［4］使用离散多项式变换（DPT，Discrete polynomial transformation）对高阶信号进行降阶，再结合PMF-FFT 的方法进行捕获，但是该方法在降阶时会引入更多的噪声，在信噪比较低时效果较差。文献［5-7］提出部分匹配滤波器和分数阶傅里叶变换（FRFT，Fractional Fourier transform）相结合的方法。通过FRFT实现了一阶多普勒变化率的补偿，但是传统的FRFT 是通过对一个二维函数进行最大值搜索，如果想要获得参数精度为0.001 的量级，需要在［0-2］内以变换阶数为自变量，以分数阶频谱峰值为检测因子，在时频面上进行峰值搜索，进行2001次FRFT，这存在运算量较大的问题。且文献［8］指出，随着多普勒变化率的增大，其捕获效率在相同信噪比条件下会随之降低。对于低信噪比条件下信号的捕获，文献［9-12］皆采用相干非相干累积的方法提升信噪比。文献［13］通过引入最大似然法来估计码相位、多普勒频偏，但是同样的，也会引起巨大的运算量，难以满足结构简单、实时性强的接收机。因此，高动态环境下信号的精确捕获受到了研究者的广泛关注。

针对存在一阶多普勒变化率的高动态BOC 信号捕获速度慢，捕获精度低的问题，本文提出基于分级PMF-FRFT结合功率谱累积的捕获算法。该算法通过PMF 实现了分段处理，减少后续FRFT 的运算复杂度，利用分级分数阶傅里叶变换结合功率谱累积快速搜索最佳阶数，通过功率谱累积平均抑制噪声，提升信号强度，然后在最优阶数下利用FRFT和功率谱累积完成对存在一阶多普勒变化率的高动态信号精确捕获。

2 高动态BOC 调制信号模型

高动态环境下，BOC 信号的接收模型可以表示为：

r(t)=Ad(t)s(t)exp[j2πφ(t) +φ0]+N(t) （1）

其中A表示信号幅度，d(t)表示导航电文，s(t)=c(t)sc(t)表示基带信号，c(t)表示伪码信号，sc(t)=sgn{sin[2πfsc(t)]｝或sc(t)=sgn{cos[2πfsc(t)]｝表示副载波信号，fsc是副载波频率，φ0表示初始相位。N(t)表示均值为0，方差为σ2的加性高斯白噪声信号。载波信号φ(t)可以表示为：

其中，fi和fd分别表示中频频率和多普勒频偏，kd表示由加速度引起的一阶多普勒变化率，φ是随机相位。经下变频、ADC 及离散采样后，BOC 信号可以表示为：

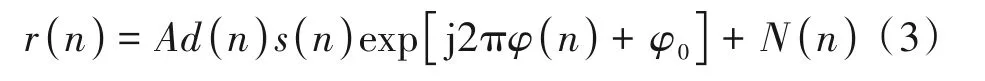
其中φ(n)=2π[(fi+fd)nTs+kd(nTs)2+φ]，N(n)为噪声，Ts表示采样间隔。

3 基于分级PMF-FRFT 结合功率谱累积的捕获算法原理

3.1 PMF过程

在存在一阶多普勒变化率的高动态直接序列扩频系统中，通常采用PMF-FRFT 算法。利用匹配滤波器实现接收信号和伪码的快速相关，利用FRFT 对多普勒变化率进行补偿，最终实现伪码相位和多普勒频偏的二维搜索。PMF 的具体过程如图1所示。

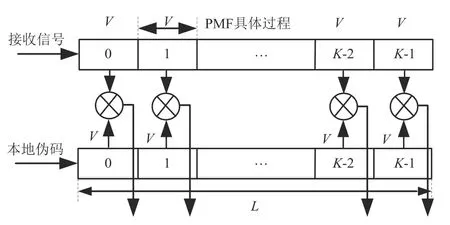
图1 PMF捕获结构图Fig.1 PMF capture structure diagram

匹配滤波器分别从接收信号和本地伪码数据各取V个进行相关运算，并作相加处理，得到第一个PMF 的输出，共取K段，得到K个PMF 的输出。这样就将长度为L的数据变为K点数据，从而减少后续的FRFT点数，加快捕获速度。

3.2 FRFT算法

一维时域信号x（t）到分数域的p阶分数阶傅里叶变换的定义为：

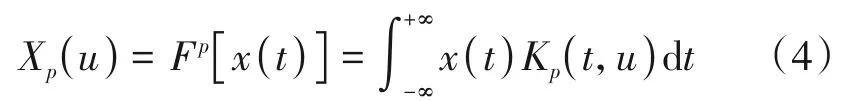
其中Fp是分数阶傅里叶变换算子。核函数Kp(t，u)可以表达为：

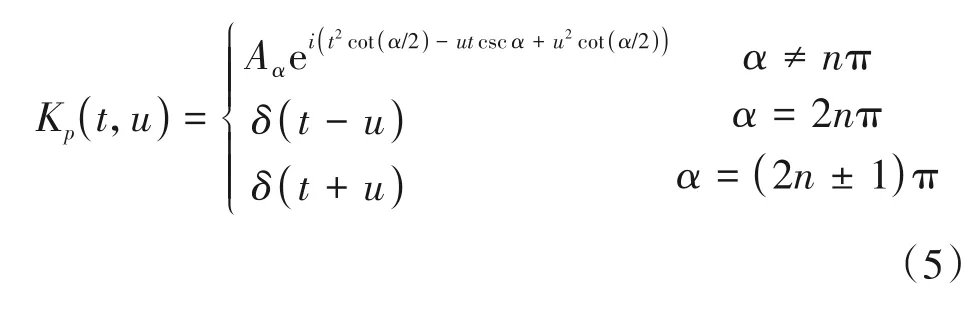
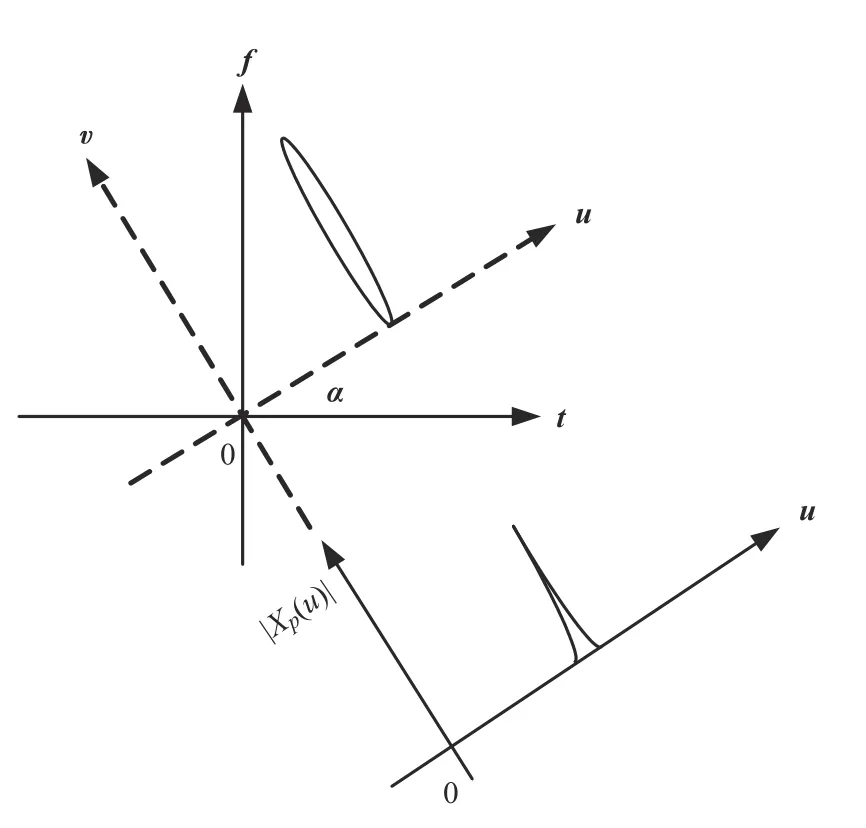
图2 线性调频信号的FRFT域表示Fig.2 FRFT domain representation of linear frequency modulation signals

其中，Xp(u)表示信号在对应阶次(p)下的分数阶傅里叶变换幅度频谱表达式。FRFT 作为一种新兴的时频分析工具，与传统的傅里叶变换方式不同，FRFT 是将变换阶次作为自变量，在最优阶数下，使线性调频信号能量表现出冲激特性。当信号伪码和本地伪码对齐时，PMF-FRFT 算法中第i个PMF输出可以表示为：

因而，存在一阶多普勒变化率的信号部分相关结果可化为：

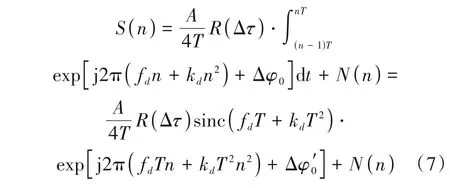
其中，R(·)表示相关函数，T表示相干积分时间，fd表示多普勒频偏，kd表示多普勒变化率，v表示匹配滤波器的长度，X表示分段数，c(n+n′)为本地伪码，N(n)为噪声，Δτ表示码相位延时误差。Δτ表示为：

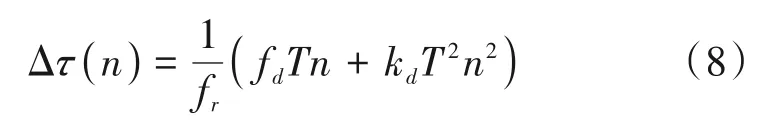
这里fr表示导航信号的射频频率。所以，存在一阶多普勒变化率的信号部分相关的结果可以看作线性调频信号。这个带噪线性调频信号S(n)在分数阶傅里叶域的输出可以表示为：

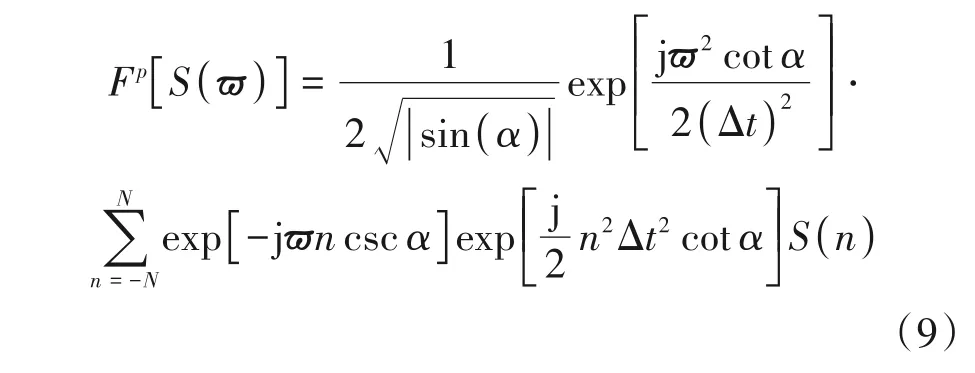
其中N表示样本数，Δt是分数域的采样间隔，ϖ=UΔt。所以，S(n)的离散FRFT输出为：

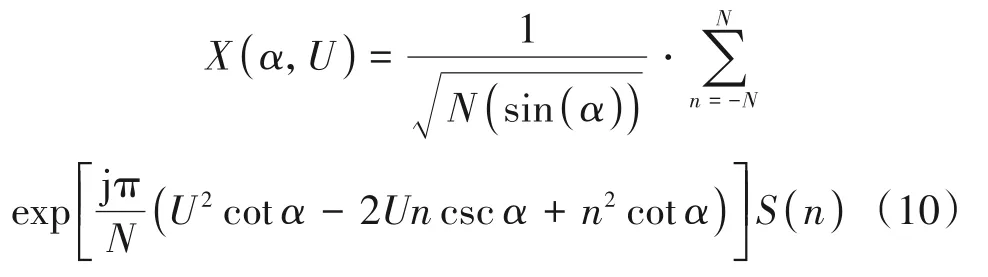
其能量的输出峰值所在位置表示为：

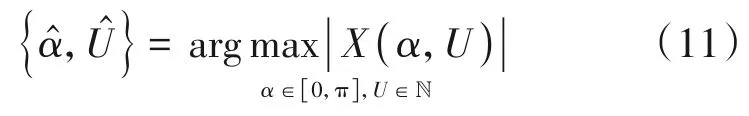
从而能够估计出多普勒频率fd以及多普勒变化率kd。

其中表示为FRFT 域旋转角度的估计值，表示FRFT 域最优阶数的估计值。因此PMF-FRFT 实现多普勒频偏估计的前提是精确获取最优阶数，在最优阶数下分析FRFT 的分数阶频谱。由文献［14］得知，在搜索最优阶数时当搜索步长达到0.001 精度量级，估计误差将不会再减小，达到CRLB 下界，此时运算量较大。于是，本文先进行参数的粗估计，然后在粗估计的小范围内再进行参数的精细估计，重复进行，采取分级迭代［15-16］的方法来降低计算量，进而达到最优阶数的快速搜索。具体流程为：

a）首先选取p的初始范围[0，2]，第一级选取搜索步长为0.1，以分数阶频谱峰值为检测因子，在FRFT 域内搜索峰值点，假设第一级搜索的阶数为a1(0 ＜a1＜2)。

b）以a1为中心，确定第二级最优阶数的搜索范围[a1-0.1，a1+0.1]，然后再取第二级搜索步长0.01，确定第二级阶数a2。

c）同理，进一步缩小最优阶数的范围[a2-0.01，a2+0.01]，以0.001 为搜索步长，寻找FRFT域内分数阶频谱最大值进而达到高精度最优阶数的搜索。

3.3 分数阶功率谱累积

通常情况下，PMF-FRFT 算法在寻找最优阶数和进行多普勒频偏估计时都是用周期图法来进行功率谱估计，但在周期图法估计的过程中，由于噪声和信号均表现出较强的随机性，其结果存在偏差。而功率谱累积平均实现了对噪声频谱的平滑处理，在降低谱估计方差的同时，也达到了精确估计的目的。

该方法描述如下：

a）匹配滤波器的输出序列做N1点FRFT 运算，则FRFT的输出分数阶功率谱向量可表示为：

P(r)表示FRFT 输出的第r点分数阶功率谱。(0 ≤r≤N1-1)

b）在接收端再顺序取接收信号和本地伪码顺序延时做部分相关处理，得到N1个部分相关值，然后重复步骤a）Q次，于是就得到了Q个功率谱的输出。

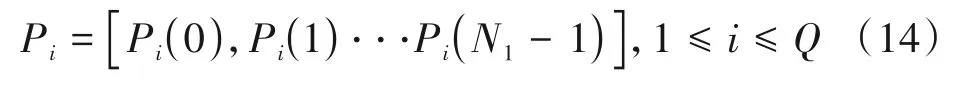
Pi(r)表示第i次第r点的分数阶功率谱。

c）将这Q个功率谱进行累积处理，累积量为，通过功率谱累积平滑噪声，从而突出信号在频谱中的精度。最后选取其中的最大值进行后续处理。

基于分级PMF-FRFT结合功率谱累积算法的捕获流程图及步骤为：

本文所提的捕获算法结构如图3所示。

图3 捕获算法流程图Fig.3 Flow chart of capture algorithm

步骤1接收到的BOC 信号经下变频、模数转换及离散采样后，被切分成K段，其中每段为V点；

步骤2将每一段信号相对应的伪随机码也做同样的处理，然后与接收信号做相关运算，接着对其加窗，做N1点分级FRFT 结合功率谱累积确定信号的最优阶数；

步骤3在最优阶数下做FRFT 运算再取模平方，然后做分数阶功率谱累积平均，提升捕获精度；

步骤4将累积后结果中最大值与预设门限进行比较，如果超过设定阈值，则说明接收信号与本地伪随机码相位对齐，捕获成功，进入跟踪阶段；

步骤5如果最大值没有超过设定阈值，则说明接收信号与本地伪随机码相位没有对齐，然后根据式（12）获得的动态参数进行多普勒频偏补偿，并滑动本地组合伪随机码，重复步骤2～4，直到捕获成功为止。

4 仿真实验分析

利用PMF-FRFT对含一阶多普勒变化率的BOC信号进行仿真分析。动态环境下含一阶多普勒变化率的BOC信号模型为：

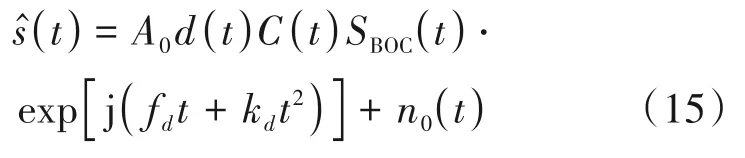
本文采用2 阶的BOC 信号，其中码速率为1.023 MHz，伪码周期长度为1023，采样频率为16.368 MHz。无特别说明，后续实验中fd=0.15，kd=0.2/N2，N2=16368 表示扩频码的采样点数。n0(t)是均值为零，方差为σ2的高斯白噪声。实验中匹配滤波器长度和分段数分别为1023 和16，使用Monte Carlo方法进行仿真。

实验1不同算法获取最优阶数

PMF-FRFT 算法捕获含一阶多普勒变化率的BOC 信号的过程中，精准的求出相关信号的最优阶数直接决定捕获的精度。为验证分级算法获取信号最优阶数的正确性，实验在SNR=-8 dB 时比较了分级和不分级算法对最优阶数的搜索，结果如图4所示。

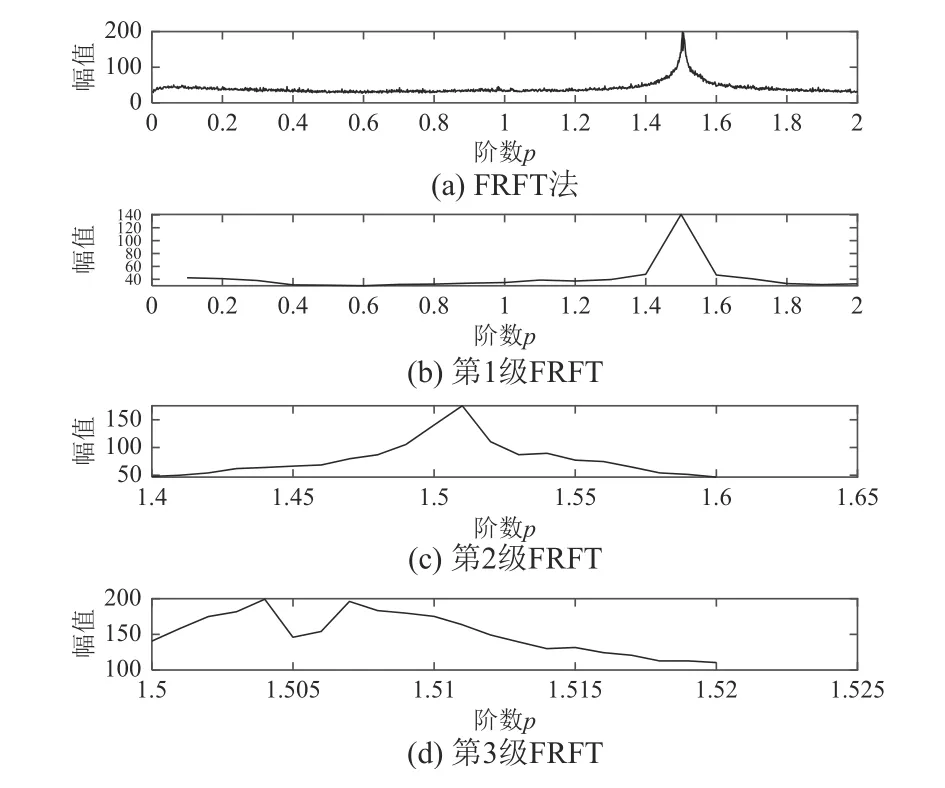
图4 不同算法对最优阶数获取精度的比较Fig.4 Comparison of optimal order acquisition accuracy between different algorithms

由实验结果可以看出，在最优阶数精度为0.001 时，两种算法均能寻找到最优阶数（p=1.504），并且都表现出明显的谱峰值。但FRFT 算法经过了2001 次运算，而分级算法只需要63 次，大大减少了运算次数，缩短了搜索时间。

实验2功率谱累积对最优阶数精度的影响

由3.2节可知，线性调频信号在FRFT域的最优匹配阶数下表现出冲激特性。实验比较了FRFT 算法功率谱累积前后信号的分数阶频谱。此时SNR=-30 dB，实验结果如图5所示。

通过图5可知，在信噪比较低时FRFT算法搜索最优阶数受噪声影响较大，谱线被噪声淹没。而通过功率谱累积Q（Q=10）次可准确突出峰值，获取最优阶数(p=1.504)。因为功率谱累积对噪声频谱进行平滑处理，降低了噪声谱的随机性，进而准确的定位最优阶数。

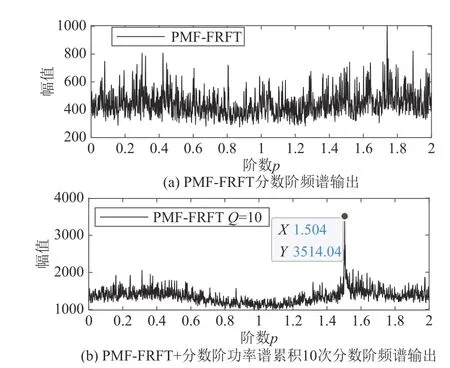
图5 不同算法对最优阶数精度的比较Fig.5 Comparison of obtaining accuracy of optimal order by different algorithms

实验3输出峰值比较

实验在SNR=-25 dB 时比较了PMF-FRFT 分级与不分级算法、累积算法对捕获峰值的影响。结果如图6所示。

由图6（a）、（b）比较可得，在相同信噪比条件下，分级捕获算法中由于噪声影响，没有明确峰值，而PMF-FRFT 算法峰值较明显。与PMF-FRFT 算法相比，分级算法会损失一定的捕获精度。比较（b）、（c）、（d）可看出，功率谱累积平均算法峰值更明显，且加窗可以突出峰值。可见，功率谱累积平均可以明显提高捕获精确性。

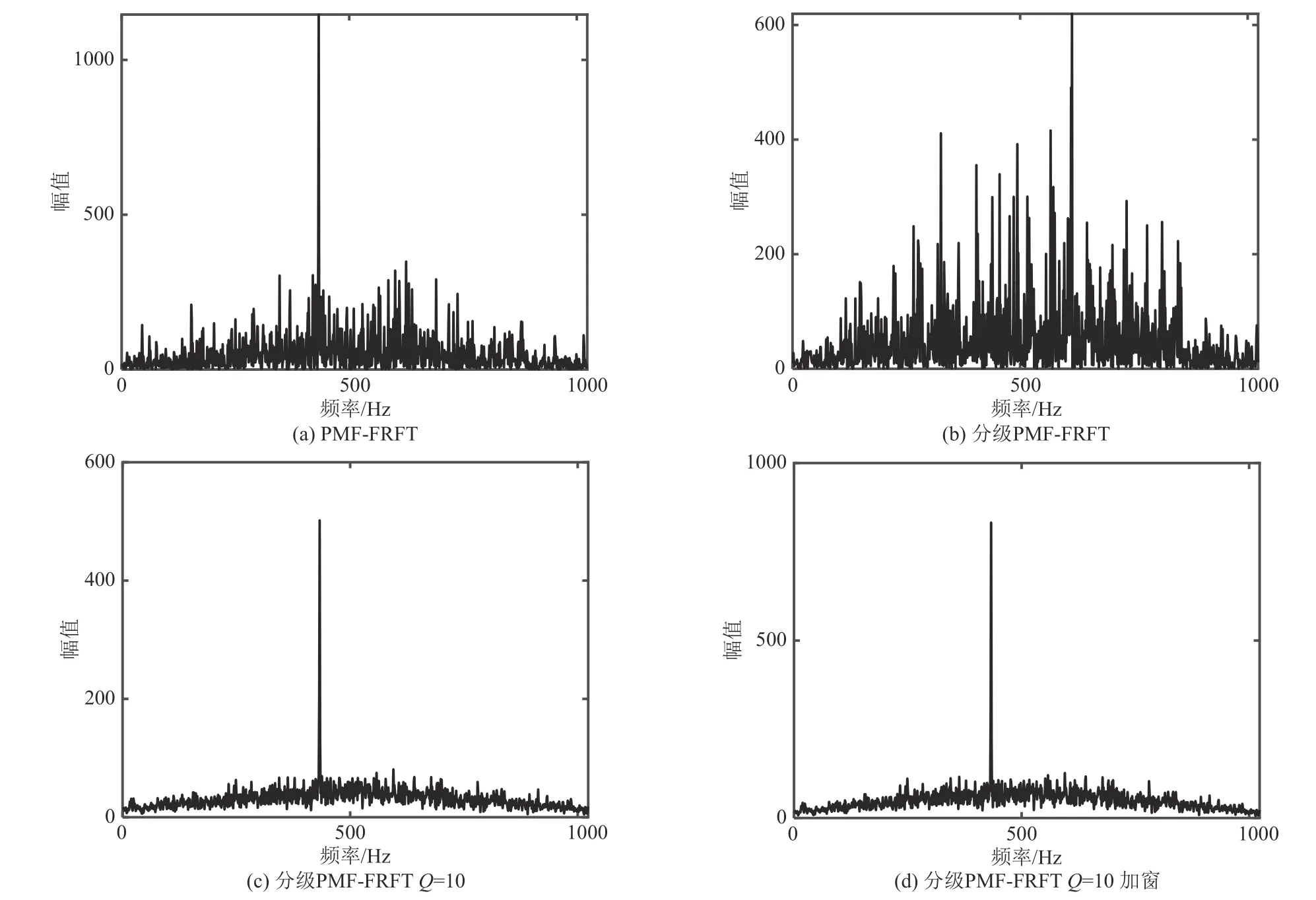
图6 不同算法输出峰值比较Fig.6 Output peaks of different algorithms

实验4不同算法在不同信噪比下的捕获概率

捕获速度是接收机性能的一个重要参数，分级FRFT 可大幅度降低运算复杂度，提高搜索速度，然而，在提升速度的同时，对捕获精度的研究非常有必要。实验在多普勒变化率为kd=0.2/N2，不同信噪比条件下，对分级和不分级的PMF-FRFT 算法的检测概率进行比较，经过1000 次Monte Carlo 仿真，结果如图7所示。

由图7可知，PMF-FRFT算法在信噪比为-17 dB左右实现对信号的捕获，而分级算法性能下降。这是由于分级迭代算法中最优阶数搜索精度下降。所以，分级FRFT 算法提升运算速度的同时捕获精度有所下降。

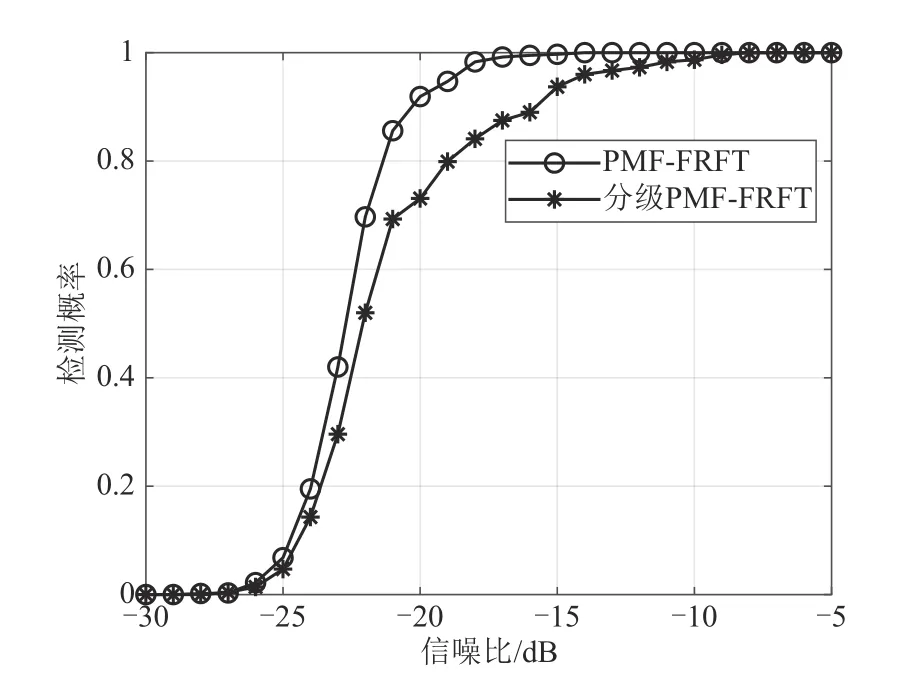
图7 分级算法在不同信噪比下的捕获概率Fig.7 Capture probability of graded at different SNR

实验5窗函数对捕获性能的影响

由于FRFT 中也会存在频谱泄露，通过加窗，可以在一定程度上减少频谱泄露。实验比较了hanning 窗、kaiser 窗、不加窗在不同信噪比条件下对检测性能的影响。经过2000 次Monte Carlo 仿真，结果如图8所示。

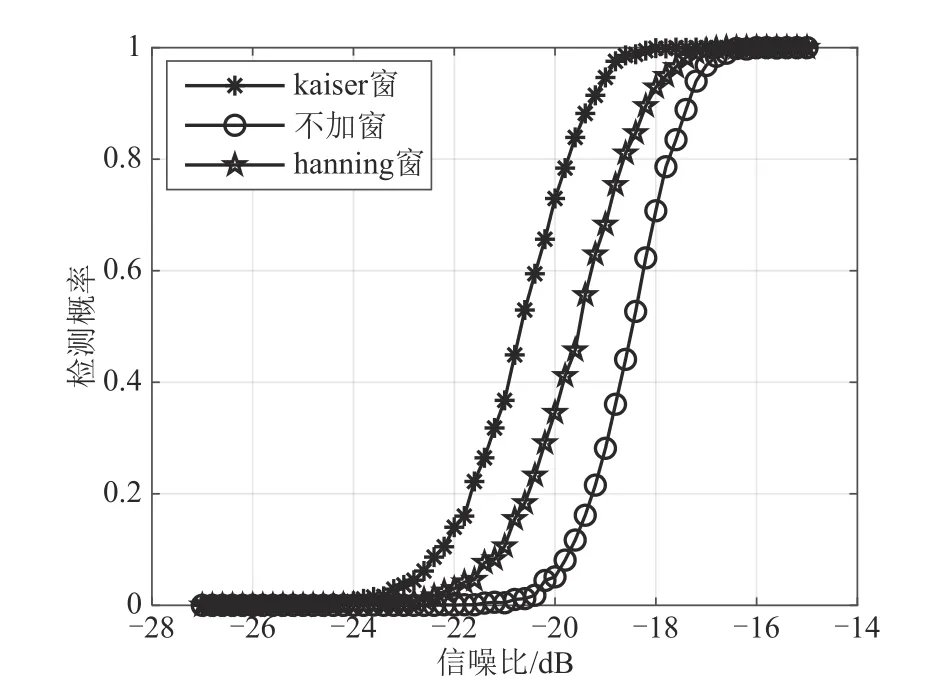
图8 窗函数对捕获性能的影响Fig.8 Impact of window functions on capture performance

由图8可知，在一定信噪比条件下，加窗可以提高检测概率。其中kaiser 窗的效果要优于hanning窗，加kaiser窗比不加窗的捕获概率提高1 dB左右。

实验6累加次数对捕获性能的影响

功率谱累积平均可以提高检测性能，实验比较了不同累积次数下的捕获概率。由分级PMF-FRFT累积算法经过1000次Monte Carlo仿真。结果如图9所示。

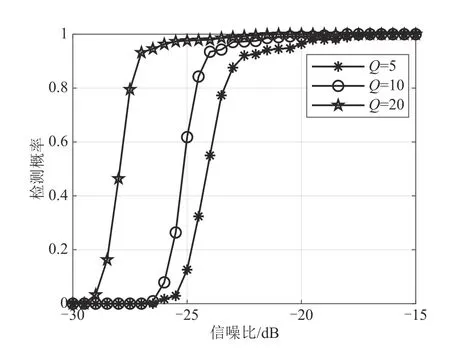
图9 不同累加次数随信噪比变化的捕获概率Fig.9 Acquisition probability with SNR variation under different accumulation times

通过理论分析和实验仿真可知，随着功率谱累积次数的增加，信号的捕获灵敏度和准确度也越来越高。当累加次数为20次时，可以捕获到-22 dB左右的信号，与图7中未累加时相比，捕获概率大约有13 dB 的提升，相比于PMF-FRFT 算法也有5 dB 左右提升。但是随着累加次数的增加，运算量会提升。在实际情况中应合理选择累加次数。

由文献［17］可知，经典的PMF-FFT 算法中PMF复杂度与FFT 操作相比可忽略不计，因此PMF-FFT同步捕获算法计算复杂度主要由FFT 操作决定。所以本文算法计算复杂度主要由FRFT 操作决定。表1 给出了不同算法之间搜索最优阶数时FRFT 运算次数的比较。

表1 不同算法搜索最优阶数时FRFT运算次数比较Tab.1 Comparison of FRFT operation times of different algorithms searching for optimal order

从搜索最优阶数时FRFT 运算次数的角度分析，在允许相同的阶次误差范围内，分级FRFT 的运算量相对于FRFT 的搜索次数大幅度降低，具有实时检测的性能。通过功率谱累积来提升搜索的精度，相同误差搜索精度下，相比于FRFT，分级FRFT功率谱累积20 次，FRFT 的运算次数也少于前者。所以综合来说本文的捕获算法可以实现较低信噪比下动态信号的快速、精确捕获。

5 结论

本文提出了高动态环境下BOC 信号的精确捕获算法，该算法首先利用PMF 实现接收信号和本地伪码快速相关，通过分级FRFT 结合功率谱累积快速搜索信号的最优阶数，减少了运算量，缩短了捕获时间。在最优阶数下利用FRFT 结合分数阶功率谱累积平均平滑了噪声，实现了含一阶多普勒变化率的动态BOC 信号的精确捕获。实验比较了分级PMF-FRFT 与PMF-FRFT 的算法，不同累加次数情况下分级PMF-FRFT算法对捕获精度的影响。仿真结果表明，相比于原始的PMF-FRFT捕获算法，本文所提方法可通过调节累积次数来适应不同噪声环境下的捕获，对于存在一阶多普勒变化率的BOC 信号，在FRFT 点数为1023 时，利用功率谱累积20 次，在SNR=-22 dB 条件下仍能实现对信号的捕获。因此，本文所提方法是一种更实用，更精确，应用范围更广的捕获方法。