基于并行ADMM算法的氢电混合微电网经济调度方法

黄 豫， 卓 越， 聂金峰， 曹 毅， 刘志文

(南方电网能源发展研究院 有限责任公司，广州 510670)

随着化石能源的长期使用，能源枯竭与温室效应的形势愈发严峻，清洁可再生能源的发展备受关注[1]。我国是全球气候治理的重要参与者，并已将碳达峰、碳中和纳入国家总体发展战略，发展新型分布式电源(Distributed Energy Resources，DER)替代污染性强的传统分布式电源成为双碳政策的关键环节。氢燃料电池作为一种既高效安全又清洁环保的发电装置，具有发电效率高、稳定性好以及无污染等特点，是一种重要的新型分布式电源。微电网[2]作为分布式电源消纳和管理的有效方式，因其能源清洁、发电方式灵活、具备储能、与环境兼容、线路损耗小等优点得到了快速的发展[3-4]。笔者考虑的微电网中含有风力发电机、光伏发电系统、氢燃料电池和储能系统，通过优化算法，以最小化电力运行成本为目标，对微电网分布式电源和储能系统进行最优功率配置，即微电网经济调度[5]，可以很好地缓解能源供应紧张和环境污染问题。

微电网的经济调度效果通常受设备建模、控制结构、优化算法等因素影响，尤其与其采用的控制结构密切相关，常用的控制结构主要有集中式和分布式2种。然而随着分布式电源的高度渗透，一对多的集中式控制将面临计算负担重、通信复杂等挑战，分布式控制应运而生。分布式控制[6]结构下的经济调度不需要集中控制单元[7]，每个分布式电源均分配一个局部控制器，所有分布式电源仅通过与相邻分布式电源之间点对点的通信就能完成经济调度，尽管分布式控制下系统架构会变得复杂，但因其可靠性更高，再加上微电网中分布式电源高分散度、易部署的分布特性，分布式经济调度逐渐成为研究热点。

研究者们对分布式经济调度已经做了大量研究：茆美琴等[8]通过引入等微增率原理提出了一种基于分布式控制算法的微电网经济调度策略。Zhang等[9]基于一致性算法提出了一种孤网无功分配方法。Zhang等[10]通过结合改进的等微增率原理和一致性算法，提出了一种自适应双控制的能源互联网优化方法。上述分布式经济调度方法虽然避免了集中式计算负担重、通信复杂的问题，但在迭代次数和收敛速度方面仍需要进一步研究改进。基于上述问题，Boyd等[11]首次基于多智能体框架提出交替方向乘子法(Alternating Direction Method of Multipliers，ADMM )解决分布式优化问题。ADMM算法结合了对偶上升[12]的可分解性和乘子法较快的收敛速度，并且不要求目标函数为严格凸形式，较其他分布式算法收敛速度更快，因此成为分布式优化领域的一种重要方法。王皓等[13]基于传统的ADMM算法提出一种微电网群双层分布式调度方法。Li等[14]结合有限时间平均一致性算法提出了分布式ADMM算法。瞿小斌等[15]基于标准ADMM算法介绍了一种高斯赛德尔型ADMM (GS-ADMM)算法，该算法可实现串行优化。针对文献[15]中串行优化存在通信延迟的问题，夏世威等[16]通过对所有变量上一次迭代的计算结果求平均值进行所求变量的更新，提出了可实现并行优化的同步ADMM算法。Deng等[17]基于雅可比ADMM算法提出了可实现全局优化近似雅可比ADMM(Proximal Jacobian ADMM)算法。然而，上述基于ADMM算法的分布式经济调度方法并不能称为真正的分布式计算，其仍需要有一个协调中心来更新每个智能体的变量值，这造成传统ADMM算法在实际使用时仍然会受制于协调中心的计算和通信能力。

针对上述问题，笔者基于对数障碍函数和虚拟智能体提出了一种改进的完全分布式ADMM算法，可实现含氢燃料电池微电网的完全分布式经济调度。不同于现有的ADMM算法，笔者分别采用对数障碍函数法和虚拟智能体的思想来处理分布式电源自身功率不等式约束和微电网功率平衡等式约束，将带约束的问题转为无约束问题，进而实现完全分布式ADMM算法求解。该算法不需要协调中心，每个变量的更新仅需相邻智能体的变量值就能完成完全分布式运算。最后利用Matlab对某30节点的微电网系统进行算例分析，通过和传统的ADMM算法进行比较，验证所提方法的可行性和有效性。

1 微电网经济调度概述

1.1 成本函数

本文所述微电网考虑了以质子交换膜燃料电池为代表的氢燃料电池(Hydrogen Fuel Cell，HFC)、以锂电池为代表的电储能系统(Energy Storage System，ESS)以及以光伏发电系统和风力发电机为代表的可再生能源(Renewable Energy Source，RES)。

整个微电网的成本函数为：

(1)

式中：fHFC,k(t)为第k个HFC在时刻t的运行成本；fESS,j(t)为第j个ESS在时刻t的运行成本；NHFC、NESS分别为氢燃料电池和电储能系统的总个数。由于现有方法对风、光以及负荷的预测精度并不高，多时段的优化效果并不能很好地调配分布式电源出力，因此本文主要研究某个时刻的实时调度，即单点优化。

氢燃料电池和电储能系统是可调度的分布式电源，而可再生能源是不可调度的，因其输出功率与外界环境相关且不可控，因此在优化调度中，需最大化消纳可再生能源发电功率，且不考虑其发电成本[3]。

氢燃料电池和储能系统的成本函数如下。

1.1.1 氢燃料电池

氢燃料电池能够在功率限制范围内将其功率调节至任意所需参考值。其运行成本函数通常表示为二次函数[18]：

PHFC=α·VH2,FC

(2)

式中：PHFC为氢燃料电池的输出功率；VH2,FC为氢燃料电池消耗的氢气体积；α为电能转化效率。

(3)

式中：ak、bk、ck为成本函数fHFC,k(t)的系数；PHFC,k(t)为第k个氢燃料电池在时刻t的功率输出。

氢燃料电池发电还需满足功率上下限以及爬坡功率的上下限约束：

(4)

(5)

1.1.2 电储能系统

电储能系统在微电网中具有双向调节能量的作用，通过电力电子设备与微电网进行电能交换，其运行成本函数[19]定义为：

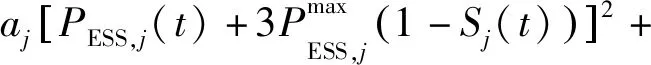
(6)

PESS,j(t)、Sj(t)需要满足如下约束：

(7)

(8)

(9)

1.2 最优功率配置

微电网中最优功率配置的目的是在满足微电网功率平衡约束和分布式电源、储能系统自身发电约束的同时，以最低的发电成本在可调度分布式电源之间分配功率输出。本文所考虑的经济调度问题可转化为式(10)中的优化问题。

(10)

式中：P(t)为所有可调度电源的发电功率总和；PRES(t)、PD(t)分别为微电网系统中可再生分布式电源的总输出功率和总负载需求；NHFC、NESS分别为氢燃料电池和储能系统的总个数。

2 基于ADMM的分布式优化算法

2.1 一致性ADMM算法

传统的采用一致性算法[20]的ADMM算法中，首先考虑如下无约束优化问题：

(11)

式(10)可以转化成如下ADMM形式：

(12)

其中，xi为式(11)中x的元素，z为常数。实际上，从约束可知所有的元素xi都相等，所以式(12)中的等式约束被称为全局一致性问题。

然后可得到相应的增广拉格朗日方程，其中λ为常数，ρ为惩罚系数：

(13)

因此，由ADMM算法可以得到：

(14)

(15)

λi，k+1=λi，k+ρ(xi，k+1-zk+1)

(16)

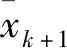
(17)

(18)

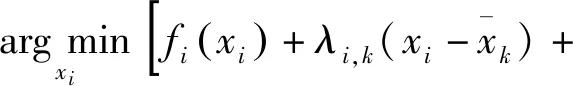
(19)

(20)

2.2 ADMM算法改进

2.2.1 优化模型的处理

由式(10)可知，优化模型包含不等式和等式约束2种约束，笔者分别采用对数障碍函数法和虚拟智能体的思想进行处理优化问题的约束条件。

一是不等式约束的处理。不等式约束的处理主要是采用障碍函数法在原来的目标函数上加上障碍函数，将目标函数的求解限制在可行域范围内。障碍函数的形式一般有分数和对数2种形式，考虑到分数形式的求导结果较为复杂，因此选择对数障碍函数来处理不等式约束。

二是等式约束的处理。等式约束描述了所有变量之间的关系，此处采用虚拟智能体的思想来解决这一问题。

虚拟智能体指的是设想的智能体，其成本函数为常函数，不存在优化变量，但满足特定的约束条件。

(21)

式中：C为常函数，满足的约束为优化问题中的等式约束。

从虚拟智能体的定义可知，只要将虚拟智能体的成本函数设为0，这样目标函数加上等式约束并不会改变整体求解结果，只是使得结果满足约束条件。这样处理有2个优势：(1) 每个智能体只需要负责满足自身的功率约束；(2) 虚拟智能体负责满足整体的功率平衡约束。

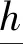
(22)

式中：Pi为每个可调度分布式电源和储能系统的功率输出。

分别采用上述不同约束对应的处理方法对目标函数进行变形，得到新的优化问题：

(23)

式中：ω为原来的智能体数与虚拟智能体数之和，规定原来智能体数目集为A，虚拟智能体数目集为B。

则新的目标函数如下：

gi(x)=tfi(x)+φi(x)

(24)

φi(x)=

(25)

由式(24)和式(25)可以看出，通过对数障碍函数和虚拟智能体对约束条件的处理，原来的优化模型变成1个新的无约束优化模型，同时新的无约束优化模型也包含一些用于调节的参数，其中t>0，tk=μtk-1，为参数t的更新公式(k代表迭代次数)，且t0>0，μ>1，v>0(v为常数)。

2.2.2 完全分布式ADMM算法

基于上述对于微电网经济调度优化模型的处理，笔者提出了一种基于对数障碍函数法和虚拟智能体的完全分布式ADMM算法，表达式如下：

(26)

λji,k+1=λji,k-ρ(xj,k-xi,k+1)

(27)

式中：N(i)为与智能体相邻的智能体集合。

由式(26)可知，变量xi的更新需要相邻节点变量上一时刻的值，并不依赖其当前时刻的值，具有完全分布的特征。因此，式(26)～式(27)中的ADMM算法仅需和相邻智能体之间进行通信，算法收敛速率更高，其算法流程如图1所示。

图1 完全分布式ADMM算法流程图Fig.1 Flow chart of fully distributed ADMM algorithm

3 算例分析

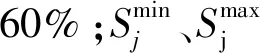
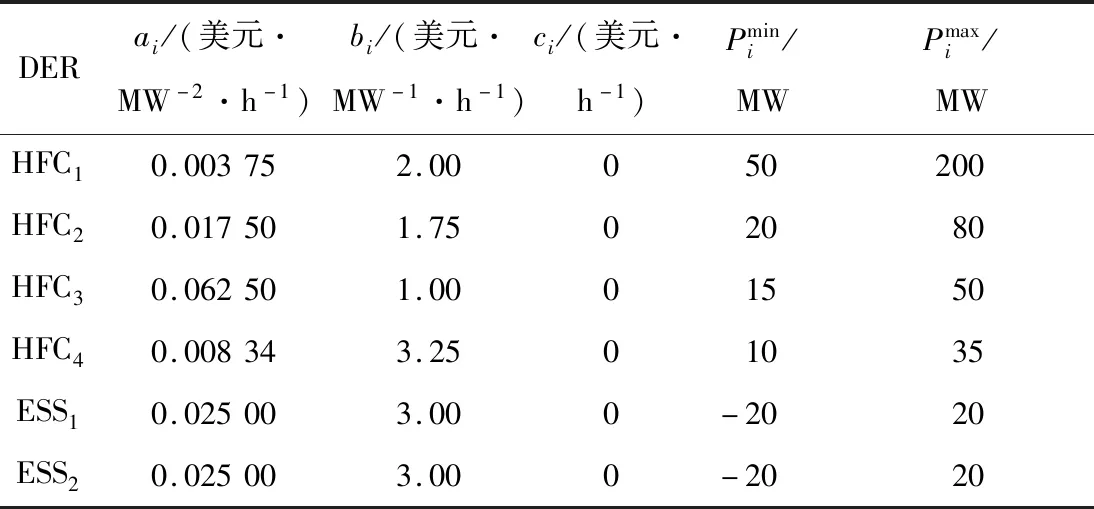
表1 仿真参数Tab.1 Simulation parameters

表2 传统ADMM算法计算结果Tab.2 Conventional ADMM algorithm results

3.1 完全分布式ADMM算法最优功率

函数值的收敛曲线如图2所示。当ρ取0.01，v取100，t0取0.01，μ取2，从图2看出所提ADMM算法的函数值最终收敛到767，与传统ADMM算法函数值相吻合。每次迭代相应DER的最优功率配置如图3所示，从图3中可以很明显看出每个DER最终的最优解与表2中算法得到的数值基本贴合，且仅迭代143次就收敛到最优解。图2和图3可以充分说明所提ADMM算法的可行性和有效性。

图2 函数值的收敛曲线Fig.2 ADMM function value convergence curve

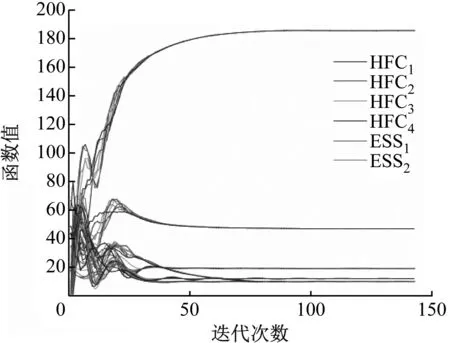
图3 每次迭代相应DER的最优功率配置Fig.3 DER optimal power configuration iteration

3.2 参数对算法收敛速度的影响

由式(26)～式(27)可知，整个目标函数的优化结果与4个可变参数密切相关，下面逐一对每个参数的选择进行分析，并探究其对算法优化结果的影响。

3.2.1 参数ρ的选择

选取μ=2，v=100，t0=0.01，保持μ、v、t0不变，改变ρ的取值来探究其对优化结果的影响。

图4给出了不同ρ取值下相应目标函数值的比较。从图4可以看出，ρ取0.01时收敛速度最快，ρ取其他值时收敛速度较慢，甚至无法收敛。

3.2.2 参数v的选择

选取ρ=0.01，μ=2，t0=0.01，保持ρ、μ、t0不变，改变v的取值来探究其对优化结果的影响。图5给出了不同v取值下优化结果误差的比较。从图5可以看出，v取100、1 000和10 000时，收敛曲线几乎一致，表明此时v取值对收敛速度的影响并不大，而当v取0.1和0.01时，难以保证算法收敛到最优解，收敛速度也就失去了意义。

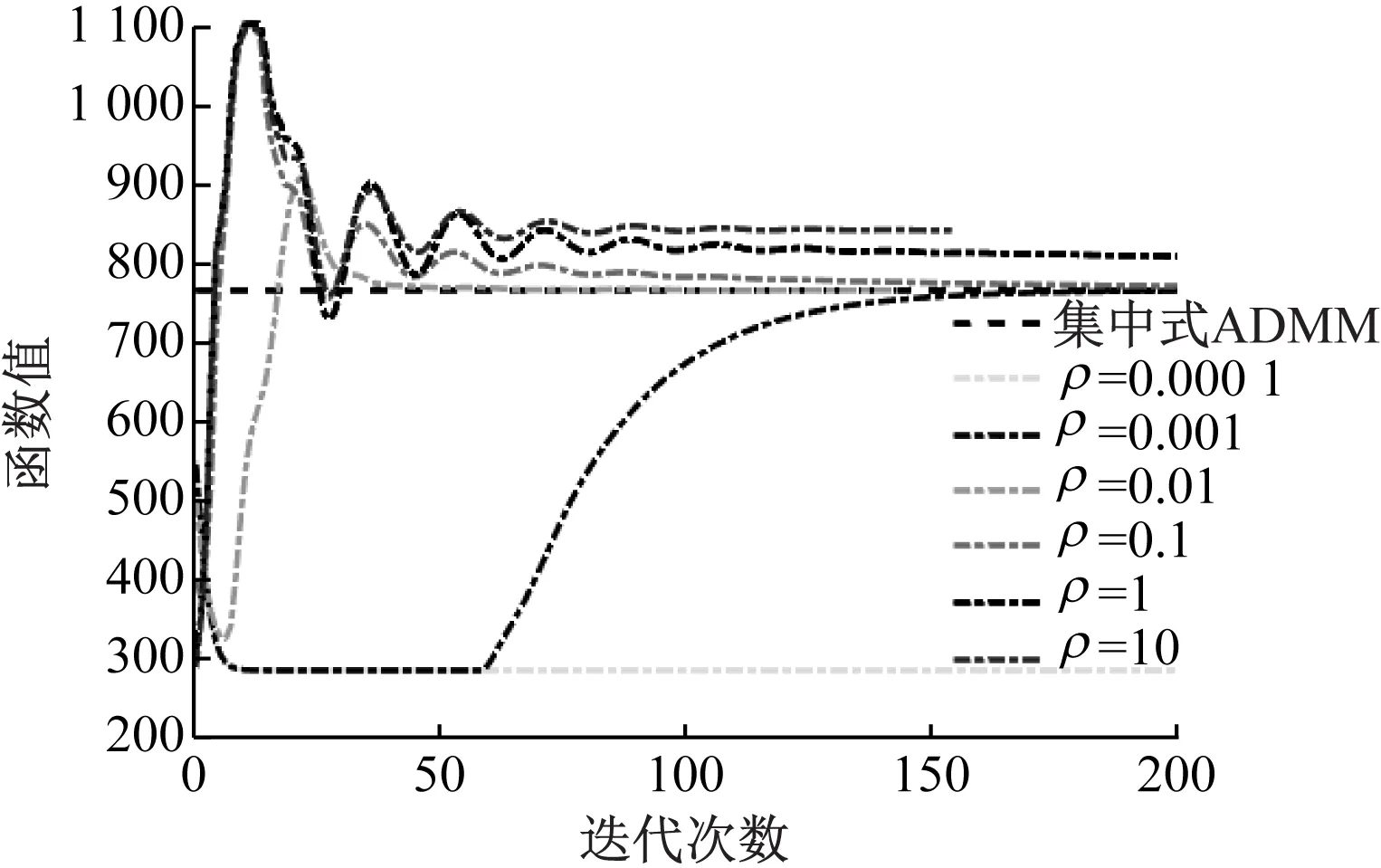
图4 不同ρ取值对目标函数值的影响Fig.4 Influence of ρ on the value of objective function

图5 不同v取值对优化结果误差的影响Fig.5 Influence of v on the errors of optimization results

3.2.3 参数μ的选择

选取ρ=0.01，v=100，t0=0.01，保持ρ、v、t0不变，改变μ的取值来探究其对优化结果的影响。

图6给出了不同μ取值下相应目标函数值的比较。从图6可以看出，μ=0.5和0.9时，目标函数值明显偏离参照函数值，且不收敛。当μ=1时，虽然可以收敛，但目标函数值比参照函数值高出许多，并没有达到最优。当μ=2，μ=3和μ=10时，3条目标函数值曲线几乎重合，表明已达到最优解。

图6 不同μ取值对目标函数值的影响Fig.6 Influence of μ on the value of objective function

3.2.4 参数t0的选择

选取ρ=0.01，v=100，由上述内容可知μ>1，可取μ=2，保持ρ、v、μ不变，改变初始值t0的取值来探究其对优化结果的影响。图7给出了不同t0取值下相应优化结果误差的比较。从图7可以看出，t0=0.000 1和0.001时迭代次数最多，收敛速度最慢，t0=1和10的误差曲线几乎一致，但是收敛速度并非为最佳。当t0=0.1和0.01时，收敛速度最快，只需143步即可达到最优值。

图7 不同t0取值对优化结果误差的影响Fig.7 Influence of t0 on the errors of optimization results

3.3 虚拟智能体数目对优化结果的影响

式(25)中B为虚拟智能体的数目，B的不同也会影响优化结果。下面选取不同数目的B探究其对优化结果的影响，结果如图8所示。

由图8可知，虚拟智能体数目越少，收敛速度越好，系统的整体负担也随之降低。

图8 不同B取值对优化结果误差的影响Fig.8 Influence of B on the errors of optimization results

4 结 语

针对微电网经济调度的分布式需求，本文提出了一种基于对数障碍函数和虚拟智能体的完全分布式ADMM算法，并将其应用于微电网经济调度。该经济调度方法具有以下几个特点：(1) 通过对数障碍函数和虚拟智能体对约束条件进行处理，大大降低了计算复杂度；(2) 所提算法为完全分布式计算，不需要协调中心，仅需要与相邻的2个分布式电源进行有限的信息交流，就能对可调度的分布式电源进行最优功率配置；(3) 相比于传统ADMM算法，该方法具有更快的收敛速度。

目前在经济调度优化模型中只考虑了分布式电源和储能自身的约束条件，没有考虑线路约束等其他约束条件，为了提高优化模型的准确度和适用范围，线路约束将是下一步研究的方向。