对2020年全国新高考Ⅰ卷导数题的再思考*
266700 山东省平度市第九中学 张 杰 姜尚鹏
276000 临沂大学数学与统计学院 薛 兵
2020年山东省实行了新高考,试卷中的导数题作为倒数第二道大题难住了不少学生,究其原因在于面对这种求参数取值范围的问题,一旦不能分离参数,或直接求导时找不到分类标准,学生就无从下手.笔者对这道题进行深入研究,发现入手方法多样.
1 试题分析
(2020全国新高考Ⅰ卷-21) 已知函数f(x)=aex-1-lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
命题立意分析:本题考查导数几何意义,利用导数研究不等式恒成立问题,考查综合分析求解能力、分类讨论思想和等价转化思想,考查逻辑推理、数学运算等核心素养,所占分值为12分.
审题及解题分析:(1)先求导数,再根据导数几何意义得切线斜率,根据点斜式得切线方程,求出与坐标轴交点坐标,最后根据三角形面积公式得出结果.(2)条件给出f(x)≥1,即研究f(x)的最值问题.先讨论特殊情况即当0
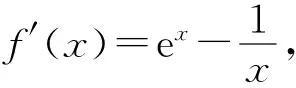
(2)①当0 ③当a>1时,f(x)=aex-1-lnx+lna≥ex-1-lnx≥1. 综上所述,a的取值范围为a≥1. 因为小问(1)比较简单,所以只对小问(2)的解法进行探讨. 解法1:①当0 综上所述,a的取值范围为a≥1. 评注:官方正解中通过对a的取值范围进行放缩,转化成上文讨论的情况,这样的解决方法是较难想到的,借助隐零点的方法解题是大部分普通层次的学生较易想到的方法,这种思路入手容易,通过隐零点满足的等式代换解决问题即可. 解法2(利用切线放缩法,先不确定a的范围):由f(x)≥1得aex-1-lnx+lna≥1.由ex≥x+1,lnx≤x-1,得ex-1≥x,-lnx≥1-x,又a>0,可得aex-1-lnx+lna≥ax+1-x+lna≥1,即(a-1)x+lna≥0恒成立. ①当a=1时,满足0≥0,所以a=1符合题意. 综上所述,a的取值范围为a≥1. 所以a的取值范围为a≥1. 所以a的取值范围为a≥1. 评注:放缩法适合水平高一些的学生使用,毕竟放缩到什么程度是放缩法的难点.建议优先考虑最简单的利用切线放缩,如ex≥x+1,lnx≤x-1,这也是放缩最常用的两个不等式,本题就可以采用切线放缩.利用a的取值范围放缩也不容易想到,建议采用更换主元的思想,将其看成关于a的函数进而放缩. 所以a的取值范围为a≥1. 所以a的取值范围为a≥1. 评注:构造同构式法是少部分高水平学生才能掌握的方法,此方法的难点在于变形构造出结构相同的函数模型,建议学生熟练掌握指数和对数的运算以及基本的函数模型,如ex与x进行四则运算以及lnx与x进行四则运算得到的函数模型. 实际上,2018年全国高考Ⅰ卷(文科)第21题就是与上述试题类似的题目.2018年高考题为已知参数的取值范围,要求证明不等式,题目如下. (2018全国高考Ⅰ卷文科-21) 已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点.求a,并求f(x)的单调区间; 2020年全国新高考Ⅰ卷第21题的小问(2),实际上是2018年全国高考Ⅰ卷(文科)第21题小问(2)的逆向问题.如果教师在讲授时有意识地对2018年试题进行改编,就可以变成2020年的试题.下面展示2018年试题的改编题. (2018全国高考Ⅰ卷文科-21改编) 已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点.求a,并求f(x)的单调区间; (2)若f(x)≥0,求a的取值范围. 改编后的2018年试题与2020年试题,两者给出的函数惊人地相似.所以教师在讲解高考题时,应研究得再深入一些,说不定下一道高考题就出自教师之手.同时可以发现,改编后的2018年试题也有三个角度的方法可供三种不同水平的学生选择,所以2020年全国新高考Ⅰ卷第21题是不可多得的好题,对教师平时的课堂教学具有良好的价值引领作用.因此,教师在高三复习时不能就题论题,而要将这道题蕴含的思想方法讲透,让不同水平的学生都能有所收获.如果教师一节课只讲这一道题的话,建议讲解时做如下改编. (2020全国新高考Ⅰ卷-21改编) 已知函数f(x)=aex-1-lnx+lna. (1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积. (2)证明:当a≥1时,f(x)≥1. (3)若f(x)≥1,求a的取值范围. 这样改编后,这道题对两道高考题蕴含的思想方法都进行了考查,同时也通过小问(2)为初次接触该题目的学生搭建了台阶,以便学生解决小问(3).思维层层递进,学生的数学素养螺旋上升,试题的育人功能得到提升.课后巩固时可以采用以下题目,此时不再需要搭建过渡的台阶,让学生课后的学习不再是简单的模仿,而是提升一个层级,将学生的学习从课堂延伸到课后,以落实学生课堂的听课效果. 巩固练习已知函数f(x)=aexlnx(其中e=2.71828…是自然对数的底数),g(x)=x2+xlna,a>0. (1)讨论函数f(x)的单调性; (2)设函数h(x)=g(x)-f(x),若h(x)>0对任意的x∈(0,1)恒成立,求实数a的取值范围.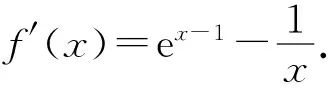
2 其他解法
2.1 隐零点法
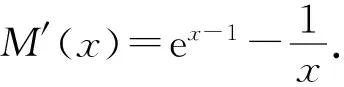
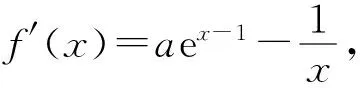
2.2 放缩法
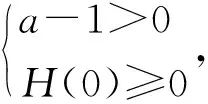
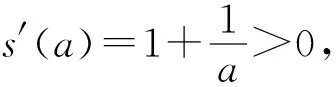
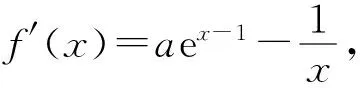

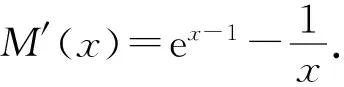
2.3 构造同构式法

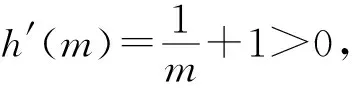
3 题目溯源

