建联系显本质 理思路融文化——“双曲线及其标准方程”的教学与反思

李 昌 (南京师范大学灌云附属中学 222200 江苏省高中数学名师工作室 213001)

凸显数学本质、建立知识体系、理清运算思路、融入数学文化、发展核心素养是数学教学应有之义．实践中如何有机结合恰到好处地发挥这些功能，是一线教师不断探索的问题．本文以“江苏省高中数学名师工作室(主持人：张志勇)”研修活动为依托，回顾反思自己的一节公开课，敬请读者批评指正．

1 学情分析

授课对象是江苏省常州市第五中学高二某班学生，他们学习基础较好，已经学习了《普通高中教科书·数学(选择性必修第一册)》的前两章，能解决直线、圆以及它们的位置关系等有关问题，对解析法有初步的认识．在第三章《圆锥曲线与方程》中，他们刚学完第1节“椭圆”，能清楚地表述椭圆的概念、标准方程和几何性质，会推导椭圆标准方程．这些认知有利于“双曲线及标准方程”的教学．

2 课标解读

圆锥曲线是平面解析几何的主要内容，《普通高中数学课程标准(2017年版)》(下称《课标2017》)指出：平面解析几何的教学，应帮助学生在平面直角坐标系中，认识圆锥曲线的几何特征，建立标准方程；运用代数方法进一步认识圆锥曲线的性质以及它们的位置关系，掌握平面解析几何解决问题的基本过程，感悟蕴含于其中的数学思想．通过圆锥曲线的教学，重点提升学生的直观想象、数学运算、数学建模、逻辑推理和数学抽象等素养．[1]双曲线与椭圆的教学内容和研究方法相似，所以双曲线的教学应具有一定的延续性和类比性．

教学目标 (1)了解双曲线的实际背景，感受其在刻画现实世界和解决实际问题中的作用；(2)经历从具体情境中抽象双曲线概念的过程，获得双曲线的概念，提升数学抽象素养；(3)经历推导双曲线标准方程的过程，培养和提升数学运算和逻辑推理能力．

教学重点 双曲线解析定义的建立和标准方程的推导．

教学难点 双曲线标准方程推导路径的选择与实施．

3 过程实录

3.1 创设问题情境

通过图1唤醒学生对圆锥截线的记忆；通过图2了解双曲线在现实生活中的运用，结合图3(动画)指出双曲线是彗星等天体的运动轨迹；提出如图4所示的问题：设A,B,C是三个不共线的监测站，B,A相距800 m，C,A相距1 000 m，信号源M与A,B,C在同一平面上．若A,B,C同时收到信号，如何确定M的位置？

图1 图2

图3 图4

生1：M在线段AB,AC的垂直平分线l1和l2的交点上，因为M到点A,B,C的距离相等．

师：很好！若将问题改为：某时刻B先收到信号，2 s后A和C同时收到该信号，其中信号传播速度为340 m/s，如何确定M的位置？

生2：M仍在l2上但不在l1上，因为M到A,B两点的距离不相等．

师：的确，但是线段MA,MB之间是否有等量关系？

生3：MA-MB=680．

师：这表明，若求出方程MA-MB=680的曲线，其与l2的交点即M的位置．由于接收信号的时间差可以是其他常数，因此一般的情形为：求平面上到两定点的距离之差等于常数的动点轨迹．

设计意图展示前三幅图片意在激发学生回顾知识源头，了解知识的应用；通过对时差定位问题从特殊到一般的抽象概括，获得研究对象，形成概念表象，提升学生抽象概括的素养．

3.2 探究双曲线定义

师：研究过与之类似的轨迹问题吗？

生4：把“距离之差”改为“距离之和”即为椭圆的定义．

师：很好！请回顾研究椭圆的思路和过程．

生4：先画出图形，根据图形建立直角坐标系，求出标准方程，再用方程研究几何性质．

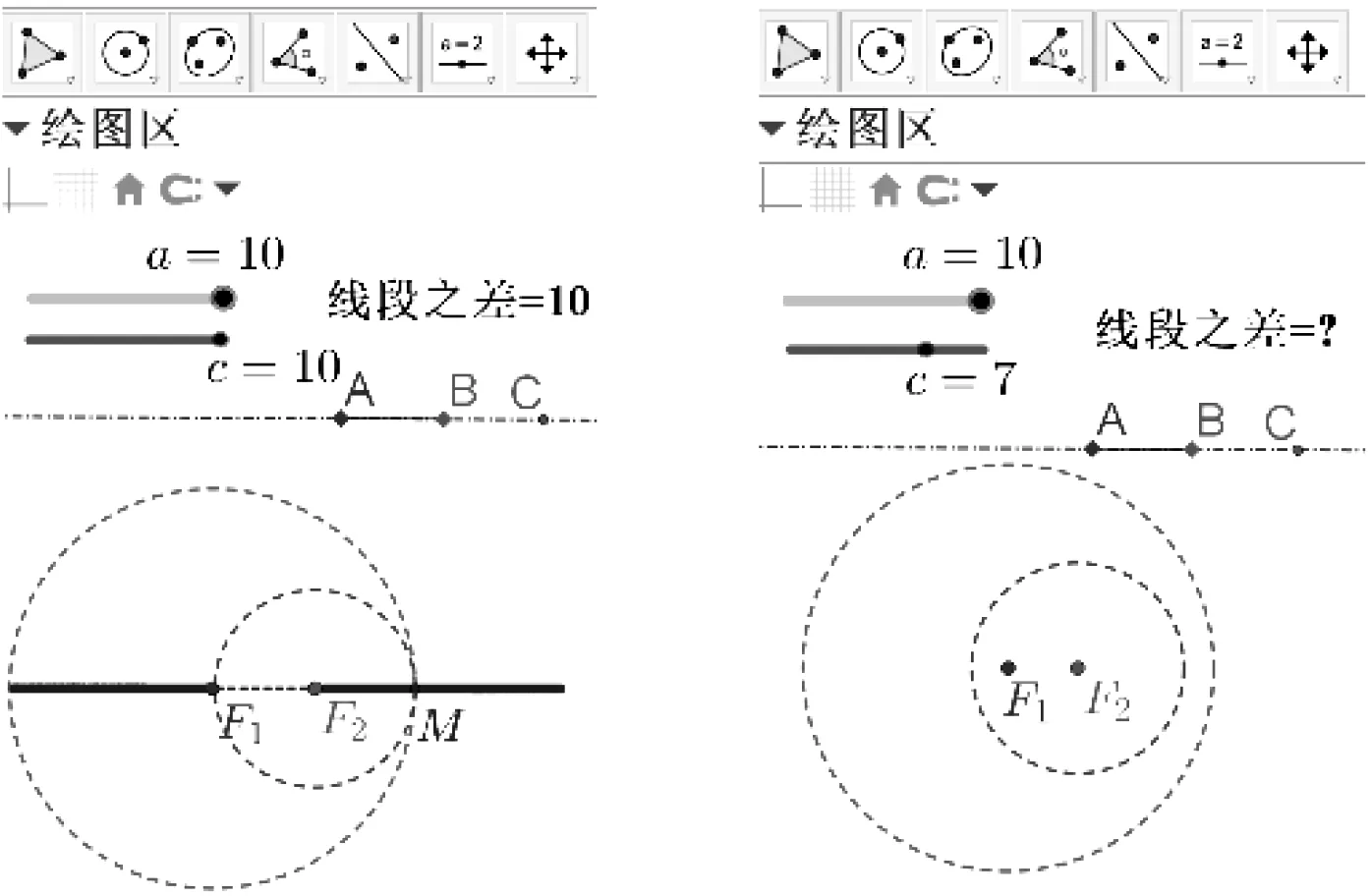
师：这是解析法的研究范式．因此，先在平面上画出到两定点距离之差等于常数的点的轨迹．到定点的距离可以转化为圆的模型，因此两个动圆的交点可以模拟动点．如 图5，在GeoGebra中取定两点F1和F2为圆心画两个相交的圆，只要保持两圆的半径之差为常数，其交点M就满足MF1-MF2为常数．为此，构造过定点A,B的直线，取其上动点C在线段AB的延长线和反向延长线上移动时，CA-CB=±AB．观察发现，当AB

图5

师：当AB≥F1F2时，点M的轨迹如何？还是双曲线吗？请预测并说明依据．

生5：不是双曲线，因为椭圆定义中有类似的限制．

师：椭圆是很好的参照对象，类比是发现结论的重要途径．改变线段AB的长度，观察交点M的轨迹形状，发现当AB>F1F2时，两圆内切，点M虽然满足到F1,F2的距离差为常数，但其轨迹不是双曲线，而是以F1,F2为端点的两条射线，如图6；当AB>F1F2时，两圆内含无交点，如图7，这表明此时点M的轨迹不存在．由此得双曲线的定义：平面上到两个定点F1,F2的距离之差的绝对值等于常数2a(0<2a

图6 图7

设计意图引导学生对比椭圆的概念，建立知识联系，探寻研究方法；运用GeoGebra动态计算和代数演算功能，演示轨迹形状，揭示概念本质；改变2a与2c的大小，通过对轨迹形状变化的观察和对轨迹存在性的思考，完善双曲线的概念，提升学生数学抽象素养．

3.3 推导标准方程

师：回顾建立曲线方程的方法和步骤，尝试建立双曲线的标准方程．

师：如果去掉绝对值，能完成化简吗？说说化简的思路．

师：很好！就是化简椭圆方程的“两次平方法”，课后自行完成吧．

生8：作差抵消相同项，但无法实施，因为它们在两个根号内．

师：这不是由双曲线定义得出的等式，若不能与定义建立联系，就毫无意义．

生10：左边是平方差，因式分解为(MF1+MF2)(MF1-MF2)=4cx，即出现定义中的距离差．

师：那如何建立联系？有何结果？

师：这有何用？

师：得出双曲线上任意一点到两焦点的距离，称为焦半径．这与两点间距离公式不同，说明什么？

师(追问)：这是由双曲线定义建立的方程吗？为什么？

生11：是，左边的焦半径由双曲线定义得出．

师：上述推导以根式为运算对象，通过平方、作差、因式分解衔接定义．这种“平方差法”最早由英国数学家赖特于1836年在《圆锥曲线之代数体系》中给出．历史上许多数学家推导圆锥曲线标准方程的方法别具智慧，如洛必塔的“和差术”、斯蒂尔的余弦定理等都值得学习借鉴，请大家课后查阅相关资料．

师：焦点在y轴上的双曲线，其标准方程是什么？

师：从双曲线标准方程的形式上，如何确定焦点的位置？

生12：是平方差等于1的代数式，焦点位置对应于被减式．

设计意图用“两次平方法”推导双曲线标准方程，是等价变形在变式情境下的迁移运用，能体现方法的一致性，但只能提升学生的熟练程度．改用“平方差法”是全新的路径，要重新选择运算对象、确定运算法则、设计运算思路，是发展学生数学运算素养的载体．告知推导方法，意在激发兴趣开阔视野．

3.4 运用数学知识

例1已知双曲线的两个焦点分别为F1(-5,0),F2(5,0)，其上一点到两焦点的距离的差的绝对值等于8，求双曲线的标准方程．(解 答略)

师：双曲线的焦点坐标既能定位又能定量，这与椭圆焦点坐标的功能一致．

师：椭圆、双曲线的标准方程形式相似，椭圆的a2比大小，双曲线的a2看符号．

例3已知A,B两地相距800 m，一枚炮弹在某处爆炸，在A处听到爆炸声的时间比在B处延迟2 s，声音的速度是340 m/s．那么(1)爆炸点M在什么曲线上？(2)这条曲线的方程是什么？

解(1)MA-MB=680，而680<800，所以爆炸点M在以A,B为焦点的双曲线距B较近的那一支上．

设计意图例1是概念在标准情境下的直接运用，意在明确焦点坐标的定位和定量作用；例2为了对比椭圆和双曲线标准方程的形式；例3是用于回应情境中的问题，引出“双曲时差定位法”建模运用，也为学习直线与圆锥曲线的位置关系埋下伏笔．

3.5 小结课堂收获(略)

4 教学感悟

4.1 双曲线的概念抽象，既要建立与椭圆的关联更要突出本质

概念教学不能“掐头去尾留中断”，也不是“一个定义几项注意”．学生只有清楚概念的来龙去脉，才能理解内涵学到“活”的知识，才能体会数学的方法、精神和思想．双曲线的概念教学应从圆锥曲线整体性的视角体现其与椭圆的关联，在获得双曲线概念表象后，才与椭圆建立联系，如此才能避开直接把“和”改为“差”带来的突兀和生硬．学生明白了双曲线的特征后，就不会纠结于为什么不研究距离之积、之商为常数的轨迹，这有利于集中思维凝练本质．

从概念的表现形态和思维形态看，教学应该经历概念抽象和符号抽象两个过程才能突出本质，根据抽象程度可分为三个阶段：简约阶段、符号阶段、普适阶段[2]．本课中，学生回顾情境、解决和抽象概括时差定位问题获得研究对象，形成概念表象，实现对双曲线的简约抽象．学生观察动点轨迹形状、验证距离差值的恒定性，获得双曲线的概念本质，实现了几何符号抽象；随着双曲线标准方程的建立，完成了代数符号抽象．改变2a与2c的大小，通过对轨迹形状变化的观察和对轨迹存在性的思辨，学生“看”到了限定2a<2c的必要性，实现了对双曲线概念的纯化，提高了概念的普适性．

4.2 标准方程的推导，既要理清运算的思路又要渗透数学文化

《课标2017》指出，数学运算表现为理解运算对象，掌握运算法则，探究运算思路和求得运算结果．其中运算思路的产生是解决问题的关键，是体现数学运算素养的精华．[3]双曲线标准方程的推导是发展学生数学运算素养的有效载体．因为运算对象和运算法则具有多样性和选择性，所以运算思路具有灵活性，但运算结果具有唯一性，这种殊途同归是数学本质和独特魅力的体现．“平方差法”推导双曲线标准方程，运算对象不是定义中距离差的等式，而是用于表达距离的两个根号，其运算思路不是“两次平方法”的等价变形，而是用平方、作差和因式分解等运算法则进行代数变形，实现与双曲线定义的衔接，获得焦半径的代数表达，从而建立双曲线的方程．这是“算两次”思想的运用和体现．

圆锥曲线积淀了数学文化，凝聚了人类智慧．在教学中选择合适的时机，以恰当的方式把数学家的方法融入课堂，让学生亲历数学家真实的思维过程，“看到”数学家当初是如何进行分析、归纳、抽象、论证的，是如何进行判断、绕过障碍、走向成功的[4]，体会数学家思考问题的角度和方法，获得数学文化的滋养，逐渐走出“知识理解”的围栏，向“知识迁移”过渡，再向“知识创新”提升[5]．