核磁共振T2 谱与孔喉半径定量关系
——兼与高压压汞法获得值对比
郑 娟, 蔡 晟, 蒋志煌, 赖秀英
( 1. 莆田学院 土木工程学院, 福建 莆田351100; 2. 亿耀 (福建) 建设有限公司,福建莆田351100; 3. 福建兴港建工有限公司, 福建莆田351100 )
0 前言
应用核磁共振(NMR)技术的分析方法, 便捷无损, 在岩土材料工程特性与微观结构特征的关系研究中发挥着越来越重要的作用[1]。 孔径分布研究作为微观结构特征研究的重要内容, 主要依托于各种岩土测试方法(一般分为直接观测法和间接测量法)。 直接观测法包括各类电镜扫描(SEM)和断层扫描(CT); 间接测量法包括气体吸附、 核磁共振、 高压压汞等。 作为间接测量方法, 能定量研究孔径分布的前提是准确完成从直接测得的物理量到孔径的转换。
核磁共振横向弛豫时间(T2, ms)谱和高压压汞进汞量都与孔隙发育程度有直观的数据联系, 众多学者据此进行了相关的研究[2-4]。 文[5-7] 提出T2谱与孔径分布呈线性关系。 而另有一些学者持不同的看法, 认为样品孔径分布的真实情况无法用简单的线性转换来实现, 并提出用幂函数转换更符合实际情况[8-10]。
本文在前人研究的经验基础上, 进一步分析核磁共振T2谱采用幂函数转换后的效果, 与高压压汞法测得的孔径分布曲线对比, 评价两条曲线的差异性, 并结合两种试验原理及样品的渗透性对出现差异的原因进行探讨, 在一定程度上对核磁共振T2谱采用幂函数转换的方法进行了合理性评价。
1 理论基础
根据核磁共振的原理, 均匀磁场中, 多孔介质孔隙中流体的T2可表示为:
式(1)中: T2为横向弛豫时间, ms; T2B为流体自身弛豫时间, ms; T2D为分子扩散弛豫时间, ms; ρ2为横向表面弛豫率, μm·ms-1; S为单个孔隙的表面积, μm2; V 为单个孔隙的体积, μm3。
通常而言, 多孔介质孔隙中流体自身的弛豫与介质表面弛豫相比要弱得多, 所以在多孔介质的研究和应用中, 1/T2B一般忽略不计; 同时,在理想的均匀磁场中, 扩散对核磁测量产生的影响也可忽略不计, 因而式(1)可简化为:

式(2)中, S/V 为单个孔隙的比表面。 对本文研究的岩石而言, 若将其孔隙简化为标准的球状或柱状结构, 那么, 比表面与孔径的关系为:

式(3)中: FS为形状系数(球形孔隙FS=3,柱状孔隙 FS= 2); r 为孔隙半径, μm。 则有:

可见, 岩石孔隙中流体的T2与r 成正比例关系。 然而, 地层孔隙结构复杂, 天然孔隙并非标准的球形或柱状。 经过大量工程试验验数据整理统计后发现, 其实T2与r 之间更符合采用幂函数转换:
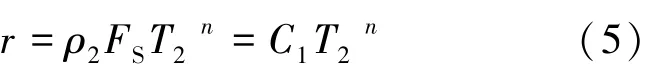
式(5)中: n 是幂指数, C1为转换系数, C1ρ2FS。
然而, 通过目前的设备和研究手段很难测得准确的ρ2和FS, 也就无法实现T2与r 的直接转换。
由高压压汞法测得的毛管压力曲线可得到岩石孔隙喉道(孔喉)的大小及与其联通的孔隙体积分布, 而完全饱和状态下岩石的T2谱可以评价孔隙大小及其对应的孔隙体积分布。 孔隙和喉道尺寸对于较均质岩层而言是由其本身粒径组成决定的, 因而两种测量反映出的孔隙分布的几何形态是一致的。 那么, T2分布曲线与孔喉半径(rt, μm)可建立相应的关系。
孔隙半径等于孔喉半径与孔喉比的乘积, 即:

代入(5)式, 整理得到T2与rt的关系:

式(6)、 (7)中: rt是孔喉半径, ct为孔喉比, C为转换系数, C = ρ2FS/ct。
从式(7)中求出C 和n 值, 便可实现T2到rt的幂函数转换。
2 T2 到 rt 的转换方法
众所周知, 高压压汞法是在真空条件下对汞逐级施加压力, 使其由大到小进入洗净烘干后的样品孔隙, 从而建立不同尺度孔隙与进汞量之间的联系[11]。 核磁共振方法针对的是洗油烘干后进行负压饱和的样品, 能定性获取样品所有孔喉分布信息[12]。 所以, 高压压汞法由于自身技术方法的因素不能反映出较小孔隙及非连通孔隙的体积, 而核磁共振法在试验样品岩心完全饱和水时的T2谱理论上可以反映出岩石所有孔隙的分布情况。 若直接将两种方法的结果进行对比, 会存在较大误差。
对于孔径大小不一的多孔介质样品, 进行高压压汞时, 汞优先进入尺寸较大的孔道, 而后增加的压力使得汞逐渐进入较小的孔道[13]。 选取rt分布与对应的T2谱进行对比分析, 绘制T2与rt的累积分布曲线, 如图1 所示。 图1 中竖直线为累积分布频率取值分界线, 该值的选取与所研究的岩体性质相关。 若研究岩体为较均质的砂岩, 该值可取为最大进汞饱和度对应的累积分布育的页岩, 该界限与微裂隙孔径大小有关, 在宁传祥等的研究中, 该值为1 μm 微裂隙对应的孔隙体积累积分布频率[15]。
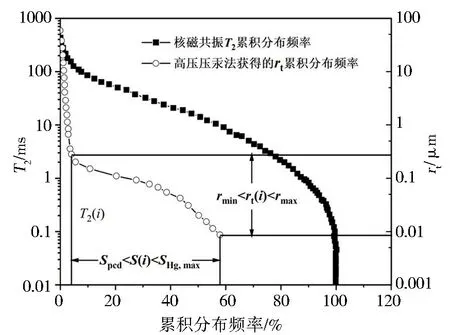
图1 T2 与rt 的累积分布频率[16]
转换过程分三步。
(1)舍去图1 中大于界限值的区域, 重新绘制T2的累积分布频率及rt的累积分布频率曲线,见图2。
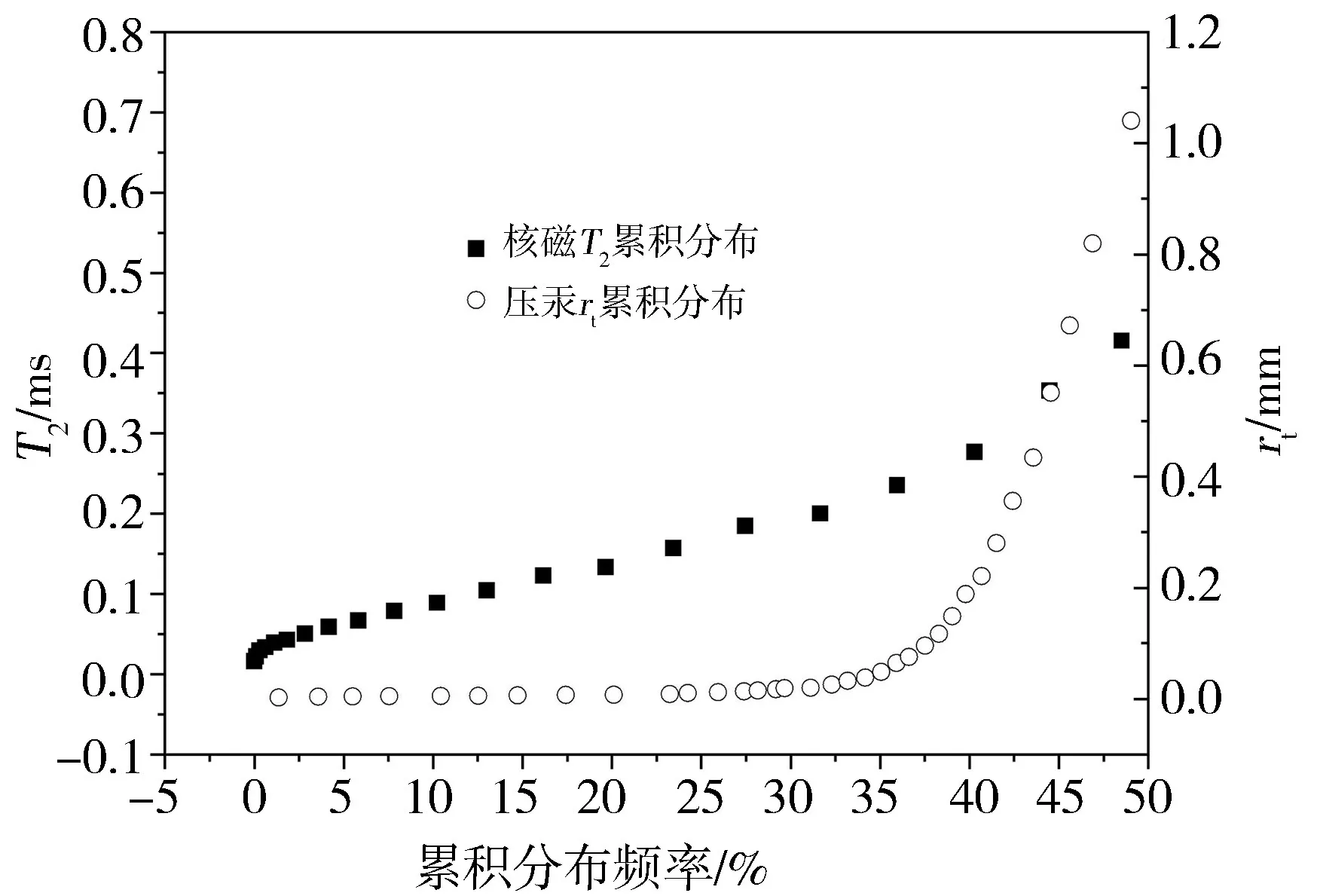
图2 界限范围内的T2 及rt 的累积分布频率
(2)在上述区域, 令孔喉半径为rt(i)时对应的累积分布频率为S(i), 将该累积分布频率插值到对应的T2累积分布曲线中, 从而获取累积分布频率为 S(i)时的T2(i), 进而得出 T2与rt的关系如图3 所示。

图 3 T2 与 rt 的关系
(3)对式(7)两边取对数, 得:

依据最小二乘法原理, 求解式(8)中C 和n的值转换为求使得下式L 最小的C、 n 值。

式(9)中, L 表示计算结果的差值, 值越小说明吻合程度越高。
确定 C、 n 值后, 回代到式(7)中, 获取 T2与rt的关系曲线。
3 转换结果及分析
3.1 转换结果
根据前文思想, 对同时开展了核磁共振和高压压汞的实验样品, 采用上述方法求取 C、 n值。 对进行了该项工作的文献进行了整理, 在下文中将一一列举有代表性且较为完整的试验, 同时进行了数据的进一步整合。
李爱芬等对19 块致密砂岩利用上述方法进行了核磁共振T2谱换算, 统计结果显示, 式(7)中n 的 范 围 为 1.00 ~ 1.43, C 的 范 围 为 0.002 ~0.016[14]。 图 4(a)为 rt与 T2的拟合结果, 图 4(b)为该批试验样品核磁共振T2谱换算的孔喉半径分布与高压压汞法获得的孔喉半径分布的对比图。
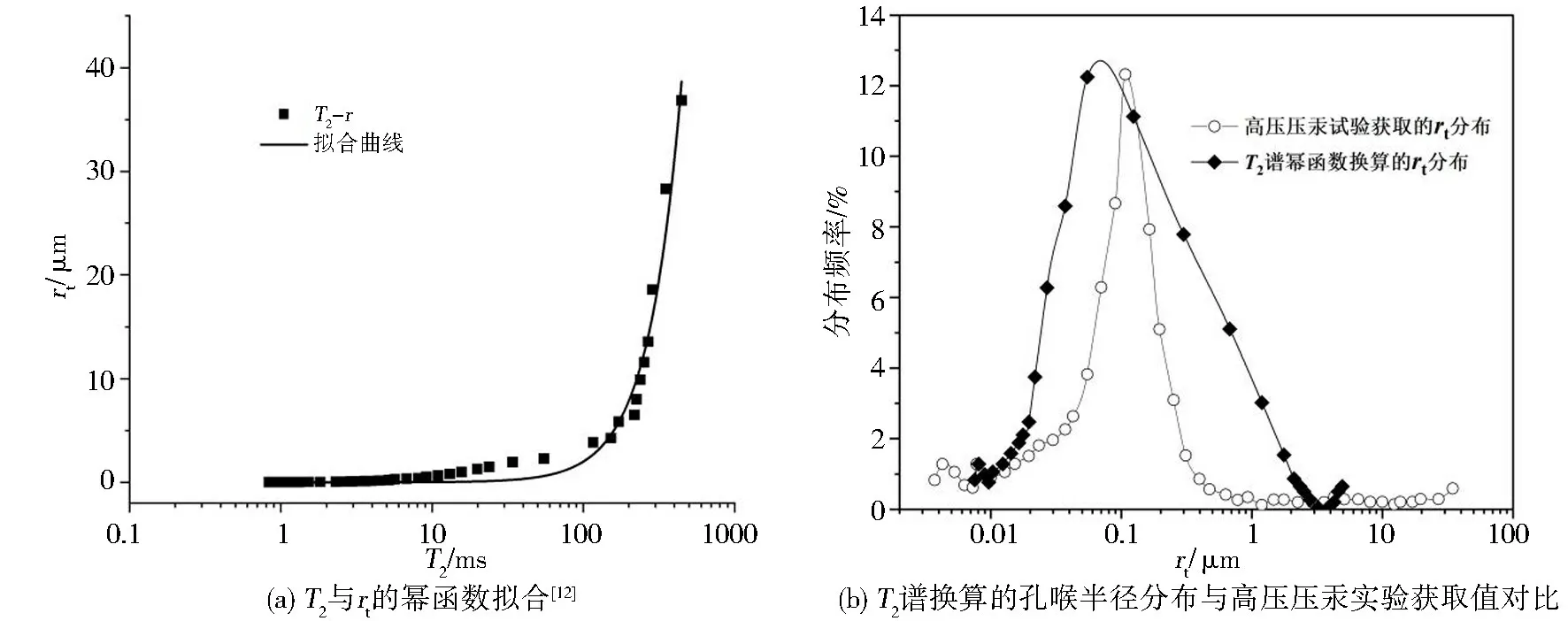
图4 文[14]T2 谱的幂函数转换结果
卢振东等对合水地区的6 块致密砂岩样品进行了核磁共振 T2谱换算, 得到 n 的范围为0.487~1.241, C 的范围为 0.000 8 ~0.010 2[16]。图5(a)为rt与T2的拟合结果, 图5(b)为该批样品核磁共振T2谱换算的孔喉半径分布与高压压汞法获得的孔喉半径分布的对比图。
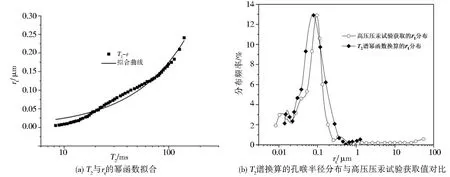
图5 文[16]T2 谱的幂函数转换结果
崔哲治等对鄂尔多斯盆地苏里格气田山西组与下石盒子组的5 块致密砂岩样品进行了核磁共振 T2谱换算, 得到 n 的范围为0. 735 ~ 1. 716, C 的 范 围 为 0. 007 28 ~0. 059 28[17]。 图 6(a) 为 rt与 T2的 拟 合 结果, 图6(b)为该批样品核磁共振 T2谱换算的孔喉半径分布与高压压汞法获得的孔喉半径分布的对比图。

图6 文[17]T2 谱的幂函数转换结果
除了上述文献对T2与rt的幂函数关系的力证, 本文对另外一些同时进行了核磁共振和高压压汞试验研究的文献[7,15,18-19]数据进行了一定的整合, 将其采用前文所述方法进行幂函数转换,图7 中(a)~(e)均为rt与T2的拟合结果。 显见,拟合程度较为理想, 说明两者之间在一定程度上符合幂函数规律。 特别指出文[7, 18]原本采用的是线性转换关系, 而在本文中改用幂函数转换如图7 中(d)、 (e)所示, 吻合程度较好。

图7 T2 与rt 值的拟合结果
3.2 两种试验方法获取的孔喉半径分布的差异性分析
在图4~图6 中的 (b) 图给出了部分试验样品的T2谱经由幂函数转换后的孔喉半径分布与高压压汞法获得的孔喉半径分布的对比图。 可以发现, 有些吻合度较高, 而有些试样通过两种试验方法获取的孔喉半径分布差异比较明显。 究其原因, 与试验样品中孔径小于图1 中rmin的孔隙和未连通的孔隙的多少有关。
为了进一步理解该差异, 整理了大量的致密砂岩及低渗透页岩的核磁共振与高压压汞试验的相关文献, 将T2谱经由幂函数转换后的孔喉半径分布与高压压汞法获得的孔喉半径的数据进行对比, 发现其基本规律是一致的, 如图8 所示。从图8 中不难看出, 两条曲线的分布趋势大致相同, 有些吻合度较高, 如图 8 中(a) ~ (d); 而有些差异较为明显, 如图 8 中(e )、 (f)。 结合渗透率研究发现, 两条曲线差异较大代表不连通孔隙分布较多, 实验样品渗透率变小, 从而使得高压压汞法测得的孔隙与实际孔隙分布相差较大。 也就是说, 样品渗透率越低, 喉道越细小,通过高压压汞法无法分析出的孔隙就越多, 从而核磁共振T2谱换算孔隙与高压压汞法获得孔隙曲线差异就越大。

图8 T2 谱幂函数换算后的孔喉半径分布与高压压汞法获得的孔喉半径分布对比
另外, 渗透率的大小不光与孔喉尺寸和连通性有关, 还和样品所含矿物成分性质有极大关系。 崔哲治等在其研究中对图8 中(e)及(f)的L4 及L5 样品进行了 X-衍射分析, 得出的结论是样品中黏土矿物含量相对较高, 大量密集填充在孔隙中, 会影响渗透率[17]。
4 结论
(1)高压压汞法与核磁共振法获取的孔喉半径分布不能直接进行对比分析, 应在rt累积分布曲线中选取一界限孔喉半径值。 该界限值对于较均质的砂岩, 可取为最大进汞饱和度对应的孔径; 对于节理裂隙较为发育的页岩, 可取此界限值为微裂隙大小。
(2)核磁共振T2谱与孔喉半径rt分布符合幂函数规律。 核磁共振T2谱通过幂函数转换后得到的孔喉半径分布曲线与高压压汞法获得的孔喉半径分布曲线的趋势一致, 说明了转换的合理性。 两条曲线吻合程度的高低与实验样品孔喉半径、 渗透性能有关, 孔喉半径越小, 渗透率越低, 通过高压压汞无法分析出的孔隙就越多, 从而两条曲线的差异就越大。
(3)在同样的孔喉半径下, 核磁共振T2谱转换后得到的孔喉半径累积分布频率多高于高压压汞法获得的孔喉半径累积分布频率, 在一定程度上证明了高压压汞法的局限性和核磁共振法的优越性。 核磁共振法可以体现所有孔隙的分布,而高压压汞法只能反映部分, 两者之间的差异体现了孔隙连通的程度。
——以西加拿大盆地A区块Upper Montney段为例

