考试实测数据三种信度估计方法的比较

周学路 任 杰

一、引言

信度指某一测验测量结果的可靠度，是衡量该测验质量的最重要的指标之一。基于真分数理论和方差分析思想，信度在经典测量理论中表示为真分数方差与观察分数方差之比，即rxx=S2T/S2X。基于这一定义产生了许多信度估计方法，其中，α 系数、β 系数和γ 系数是三种常见的、具有代表性的信度估计指标。一直以来，经过Cronbach 公式化后的α 系数[1]几乎成了测验信度的代名词，但它很明显地受到一些与信度定义无关的因素的影响，尤其是测验同质性和被试同质性，在这种情况下，陈希镇和谢小庆先后分别提出了β 系数[2]与γ 系数[3]对其进行优化。从理论与计算公式上来说，β 系数降低了信度估计对题目高同质性的依赖，γ系数又在此基础上降低了被试同质性程度对信度估计的影响，二者均在不同程度上优化了α 系数。那么，在实际应用中，三者在信度估计方面的效果究竟如何？以下基于某考试实测数据对此进行研究。

二、三种信度系数

（一）α系数

经过Cronbach 公式化后的α 系数的计算公式如下：

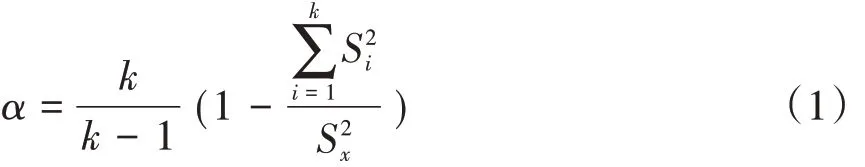
其中，k为测验包含的题目数量，S2x为测验总分方差，S2i为第i题的题目方差。

该公式的另外两种表达方式为：

其中，δ2p为真分数方差分量的估计值，δ2pi为相对决策误差方差分量，k为项目的个数。

其中，MSp为真分数均方，MSpi为误差均方。

α 系数凭借其计算简单易行和稳定性、优于分半信度估计等优点，逐渐成为应用最广泛的信度系数。但是α 系数受到诸多方面因素的影响，如题目数量多少、题目同质性高低、被试同质性高低等，这在某种程度上与信度的定义相左[4-6]。

（二）β系数

由于α 系数受题目同质性程度影响较大，当题目同质性程度较高时，即题目得分具有较高的相关、测验测量的能力维度较为集中时，α 系数可以作为信度和同质性的测量指标，如果测验的同质性程度不高或者测验异质，α 系数就会低估测验信度。为了降低测验同质性高低对信度估计的影响，陈希镇提出了β系数。β系数的计算公式如下：

其中，k为测验包含的题目数量，ρ为各题两两相关系数的最大值，S2x为测验总分方差，S2i为第i题的题目方差。

β 系数出于对题目间相关程度的考虑，实际是在题目同质性不高或异质时，对在题目同质性较高时的α系数进行了“放大”。

（三）γ系数

β 系数降低了信度估计对题目高同质性的依赖，为了降低被试同质性程度对信度估计的影响，得到对信度这一测验本身性质的更加精确的估计，谢小庆提出了γ系数。γ系数的计算公式如下：

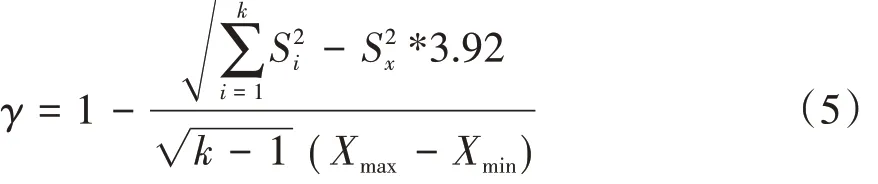
其中，k 为测验中包含的题目数量，S2x为测验总分方差，S2i为第i题的题目方差，Xmax为测验得分中的最高分，Xmin为测验得分中的最低分。

由此可导出以下两个公式：

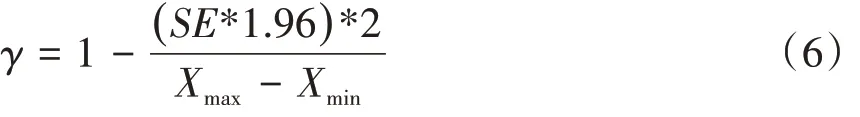
其中，SE为标准误。

其中，σ为测验标准差，α为α系数。

由公式（6）和公式（7）可知γ 与标准误和α 系数的关系。而与α 系数相比，标准误具有更高的稳定性，并不因被试同质性程度的变化而出现太大的变化。因此，利用标准误进行信度估计更加可靠。

三、研究思路与方法

（一）研究思路

基于某次考试的实测数据执行多种抽样方案，对各个样本进行描述性统计并利用α系数、β系数和γ系数对不同样本进行信度估计，比较不同的分数分布形态和不同的分数变异对三种信度系数的影响。

（二）研究设计

1. 研究对象

研究使用某考试的实测数据，该考试试卷结构如表1所示：

表1 某考试试卷结构

采用因素分析的主成分分析方法对该考试作答 数据进行分析，结果如表2所示：

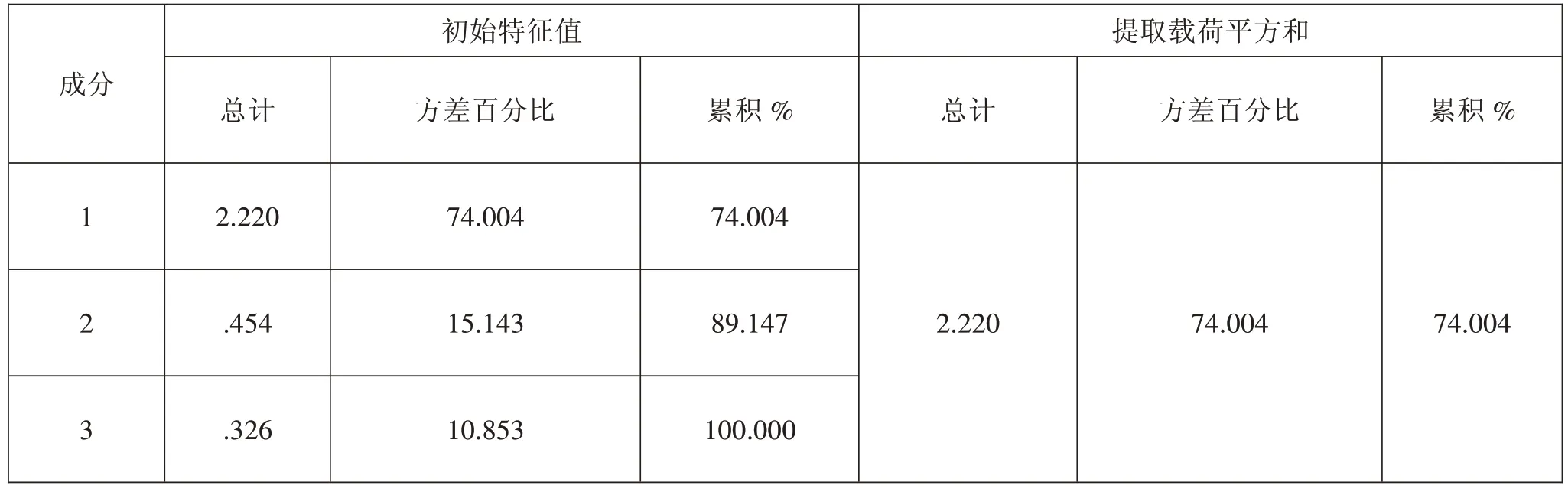
表2 某考试试卷因素分析之总方差解释

该考试三个分测验作答数据的相关性如表3所示：

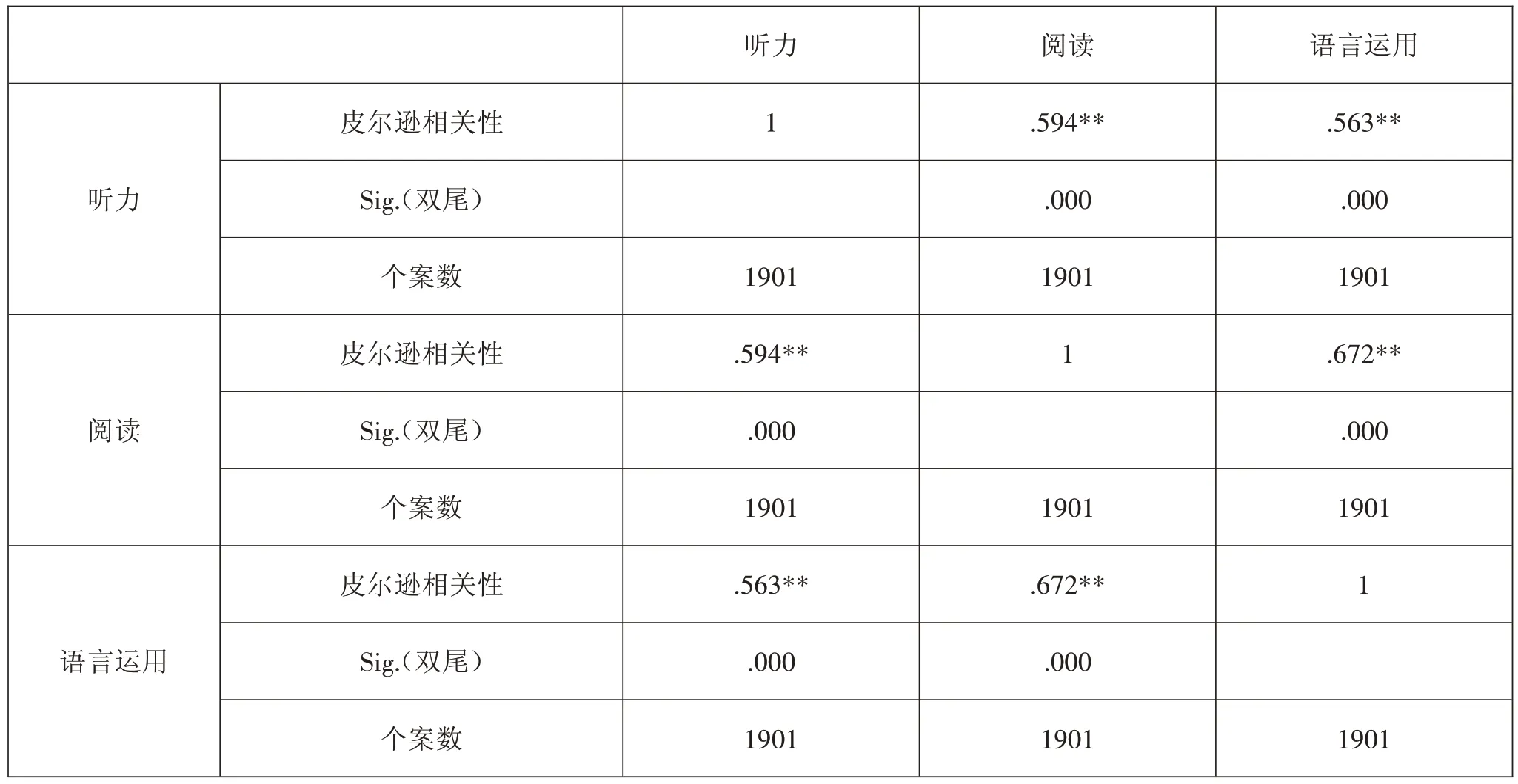
表3 某考试分测验相关性

如表2 和表3 所示，抽取的特征值大于1 的因素只有一个，能够解释总方差的74.004%，其方差占比为第二位因素的4 倍以上（一般认为第一个因素方差所占百分比是第二个因素方差所占百分比的3 倍或5 倍以上，测验基本满足/满足单维性假设），三个分测验的相关性为中强度相关，故该测验所测能力维度较为单一，题目同质性较高。

该考试描述性统计和分数分布直方图如表4 和图1所示：

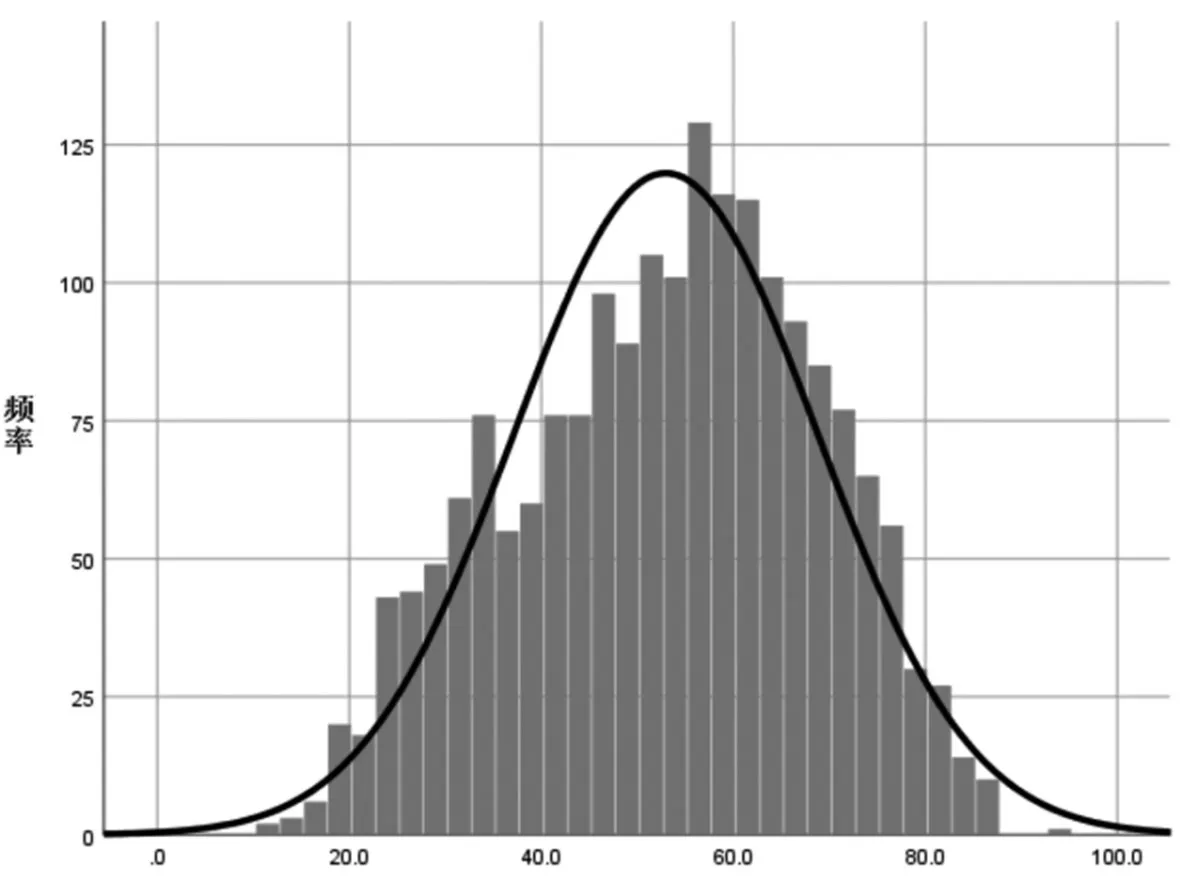
图1 某考试分数分布直方图

表4 某考试原始样本描述性统计

该考试的原始样本的样本量为1901，最高分为93.5，最低分为11.5，全距为82，均值为52.96，标准差为15.816，偏度为-0.211，峰度为-0.683，分数分布形状可视为稍平缓的近似正态分布。

2. 抽样方案

原始样本的分组情况如表5所示：

表5 某考试原始样本分组情况

将原始样本1901 人按分数高低分为高、中、低三组，其中，高、低两组的被试比例和被试数量均为27%和513人，中等分组的被试比例和被试数量分别为46%和875人。

为了验证 α 系数、β 系数和 γ 系数估计信度时受被试同质性和分数分布形状影响程度的大小，按照不同的被试比例和分布形态执行了八次简单随机不重复抽样。抽样方案如表6所示：

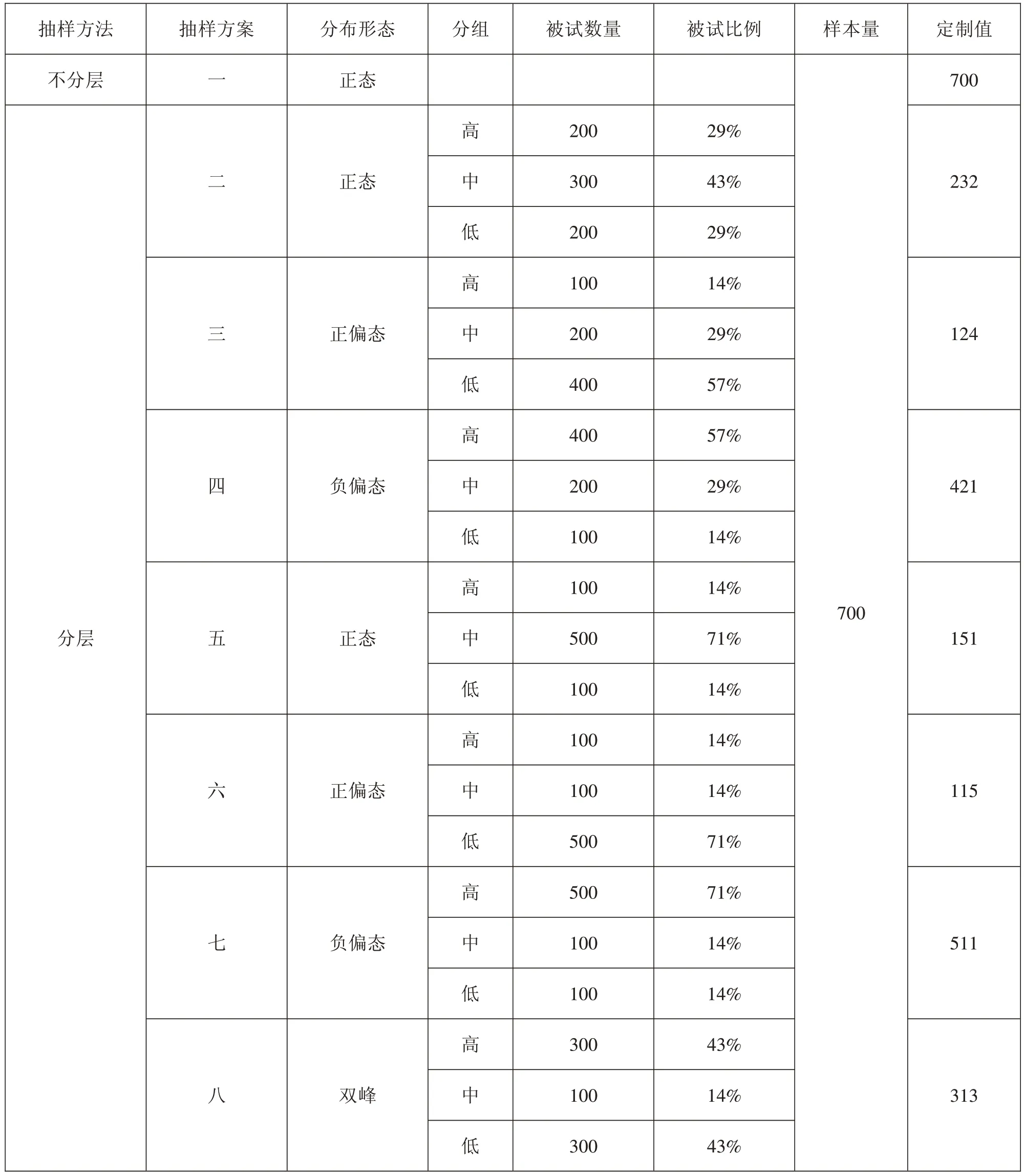
表6 抽样方案

为尽可能控制无关变量，抽取的各个样本的样本量均为700。其中，方案一是从原始样本中进行不分层简单随机抽样所抽取的正态分布的样本，用来作为样本间比较的“原始样本”，方案二到方案八是从原始样本中进行分层简单随机抽样所抽取的不同分布形态的样本。

四、研究结果

使用 SPSS、Visual Fox Pro 和 Excel 对各样本数据进行分析，结果如下：

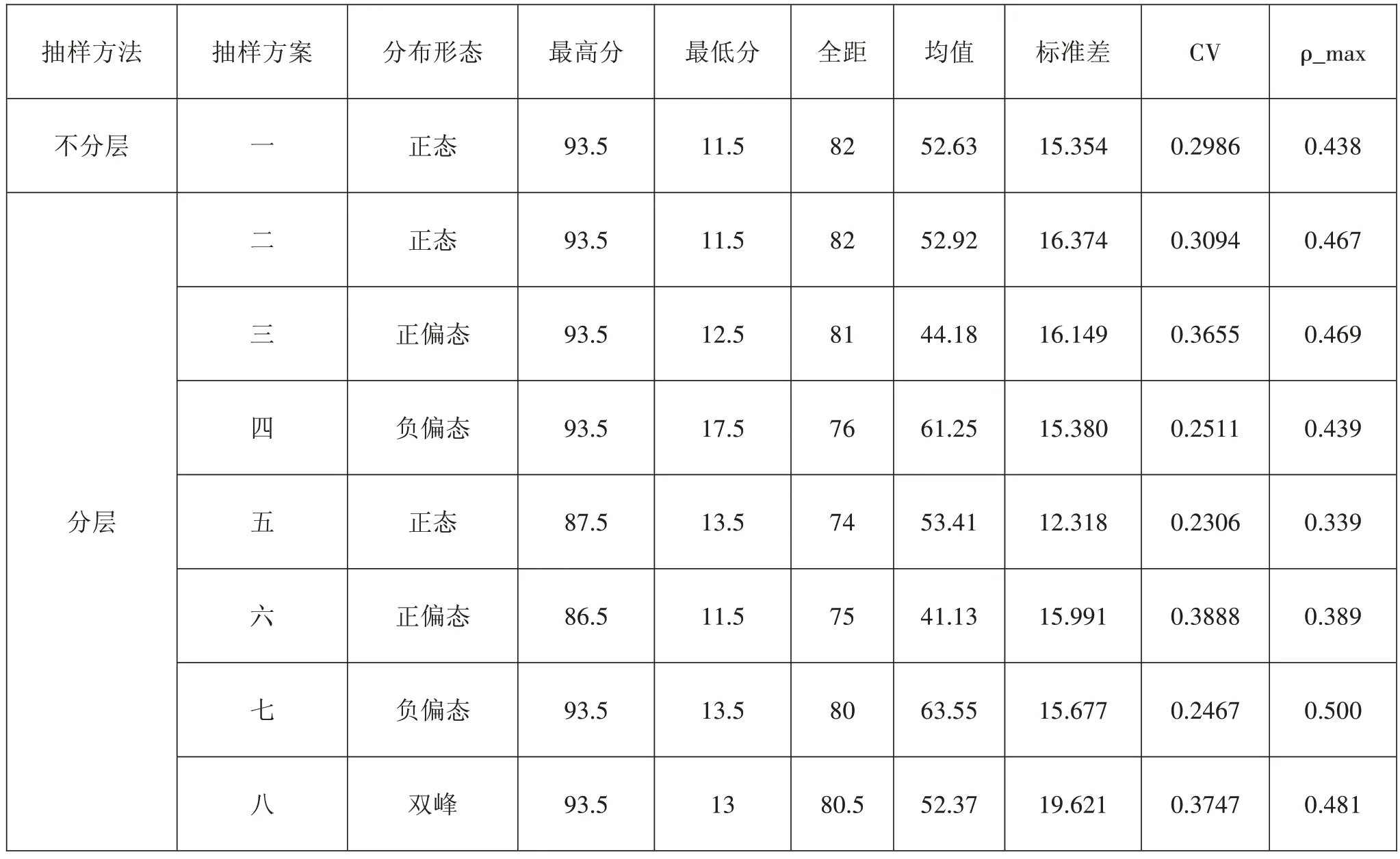
表7 各样本描述性统计与题目间的最大相关系数

表8 各样本信度估计结果

图2 横坐标中的汉字为样本编号，字母为分布形态缩写（N、PS、NS、B 分别对应正态、正偏态、负偏态、双峰），数字为该样本对应的标准差。

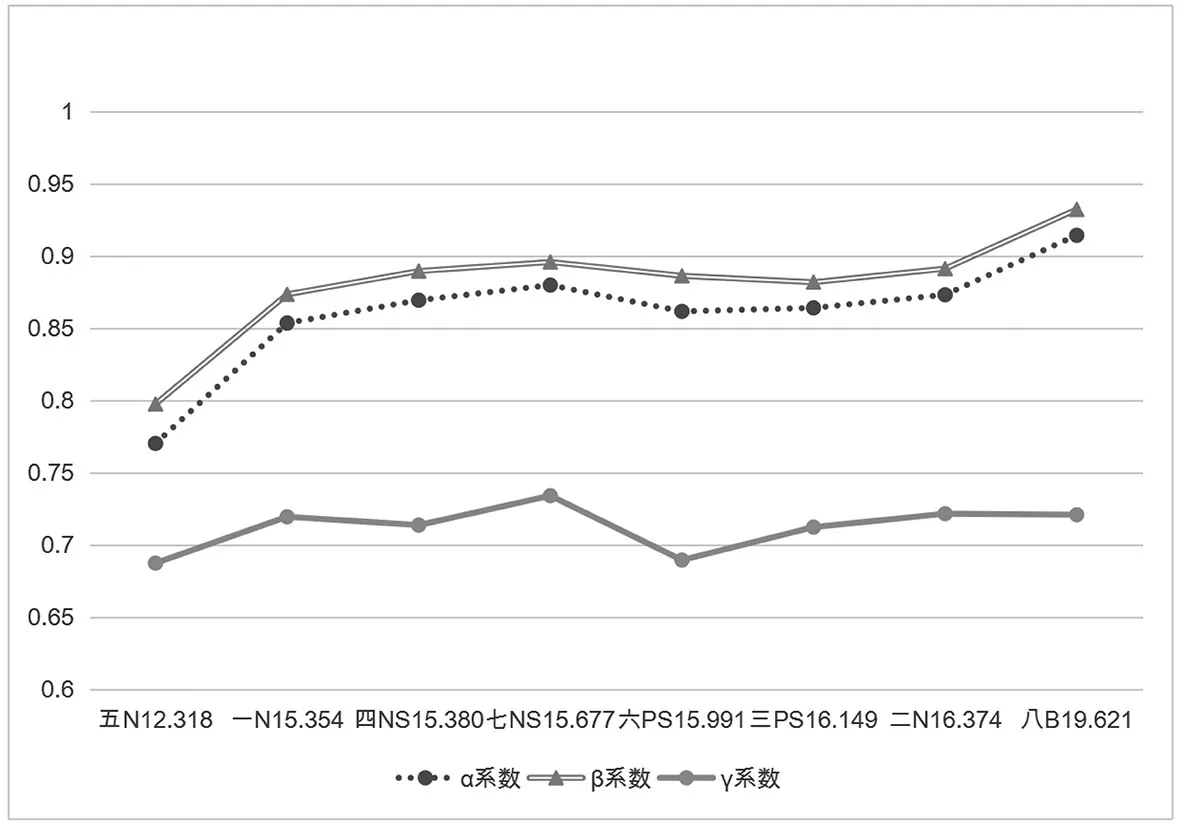
图2 三种信度系数与标准差的关系

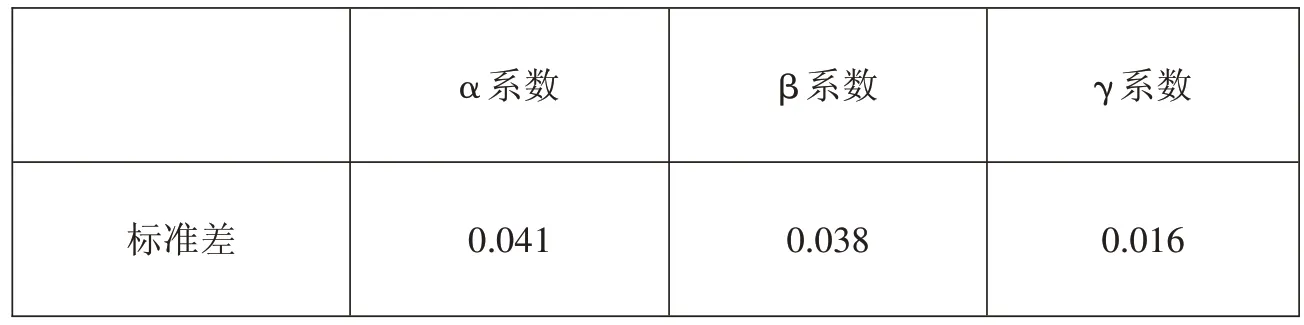
表9 基于抽样对三种信度系数标准差的估计

结合上述图表可知，从总体上看，在对某一样本进行信度估计时，三种信度系数的大小关系为β 系数＞α 系数＞γ 系数。当被试分数标准差和变异系数相近，即被试同质性程度相近，且分数分布形态相同时，如样本三和样本六、样本四和样本七，三种信度系数均具有较好的稳定性；当被试分数标准差和变异系数相近，即同质性程度相近，而分数分布形态不同时，如样本一和样本四、样本二和样本三，三种信度系数亦均具有较好的稳定性；当分数分布形态相同，而被试分数标准差和变异系数差异较大，即被试同质性程度不同时，如样本一和样本五、样本二和样本五，γ 系数表现出比α 系数和β 系数更强的稳定性；当分数分布形态不同，且被试分数标准差和变异系数差异较大，即被试同质性程度不同时，如样本五和样本八，γ系数表现出的稳定性更加明显。

基于抽样对三种信度系数标准差的估计结果显示，α 系数和 β 系数的标准差均在 0.04 左右，γ 系数的标准差仅为不到0.02。由此可知，特别是当原始数据样本量较大，而基于抽样进行信度估计时，γ 系数的稳定性将得到凸显。即便是基于原始数据进行信度估计，γ 系数的稳定性优势也不可忽视，因为所谓的原始数据实际上也只是从总体中抽出的一个样本而已。

五、结论

从标准差来看γ 系数是一种比α 系数和β 系数更加稳定的信度系数。当被试同质性程度相近时，无论分数分布形态是否相同，三种信度系数均具有较好的稳定性；当被试同质性程度不同时，无论分数分布形态是否相同，γ 系均数表现出比α 系数和β 系数更强的稳定性，尤其是当分数分布形状不同时，γ系数表现出的稳定性更加明显。

就信度估计结果而言，γ 系数比 α 系数和 β 系数低，存在低估信度的可能。一般情况下，在对某一样本进行信度估计时，三种信度系数的大小关系为β系数＞α 系数＞γ 系数。β 系数未得到广泛应用，可能与其信度估计结果和稳定性同α 系数的信度估计结果和稳定性差距微小有关；γ 系数未得到广泛使用，可能与其信度估计结果与α 系数和β 系数的估计结果相比偏低有关，既然β 系数可以出于对题目间相关程度的考虑，相当于在题目同质性不高或异质时对在题目同质性较高时的α 系数进行“放大”，γ系数或也可参考此法进行适当修正。