基于自适应预瞄前馈控制的智能车辆路径跟踪研究
杨腾盛,郭世永
(青岛理工大学 机械与汽车工程学院,青岛 266525)
近年来,智能化与自动化成为车辆发展的重要方向,其中智能车辆的路径跟踪性能决定了车辆在运动过程中能否保持稳定和安全[1],因此其逐渐成为智能车辆控制研究的热点[2]。王荣本等[3]使用预瞄及线性二次型控制器(Linear Quadratic Regulator,LQR)理论设计了智能车辆横向控制器,并针对最优控制器中的加权系数和预瞄距离进行了优化,最终通过仿真验证了控制器性能。赵治国等[4]设计基于粒子群多目标优化预瞄距离自适应寻优算法,同时结合滑膜控制器实现智能车辆的横向控制。高琳琳等[5]提出了一种基于车-路位置关系的参数优化LQR控制器,并结合前馈控制,最终得到较好的跟踪效果。XU等[6]通过求解横向误差LQR问题,利用前馈与反馈结合策略实现了车辆横向控制。目前研究中自适应预瞄更多的是应用于反馈控制器,仅有少量自适应预瞄算法与前馈控制结合的横向控制研究;同时研究大都将前馈控制用于车辆弯道时进行补偿,控制主体仍是反馈控制算法。
为实现智能车辆高精度稳定地实现路径跟踪控制,本文首先设计了根据车速、道路曲率以及相对航向偏差的自适应预瞄算法,并基于自适应预瞄结果设计了前馈控制器,为车辆提供了一个趋向于目标路径的前馈转角;其次设计了线性二次型调节器(LQR),并结合前馈控制器建立了自适应预瞄前馈LQR控制;本文控制算法是以前馈控制器为控制主体,反馈控制器作为补偿进行路径跟踪控制。最后通过Carsim-Simulink联合仿真平台对比分析自适应预瞄前馈LQR控制器,验证其路径跟踪效果。
1 车辆动力学建模
本文所建立动力学模型主要应用于智能车辆的路径跟踪领域,研究分析的是智能车辆行驶过程中所涉及的横向及横摆动力学特性,同时引入目标路径,因此建立二自由度车辆误差模型,如图1所示。
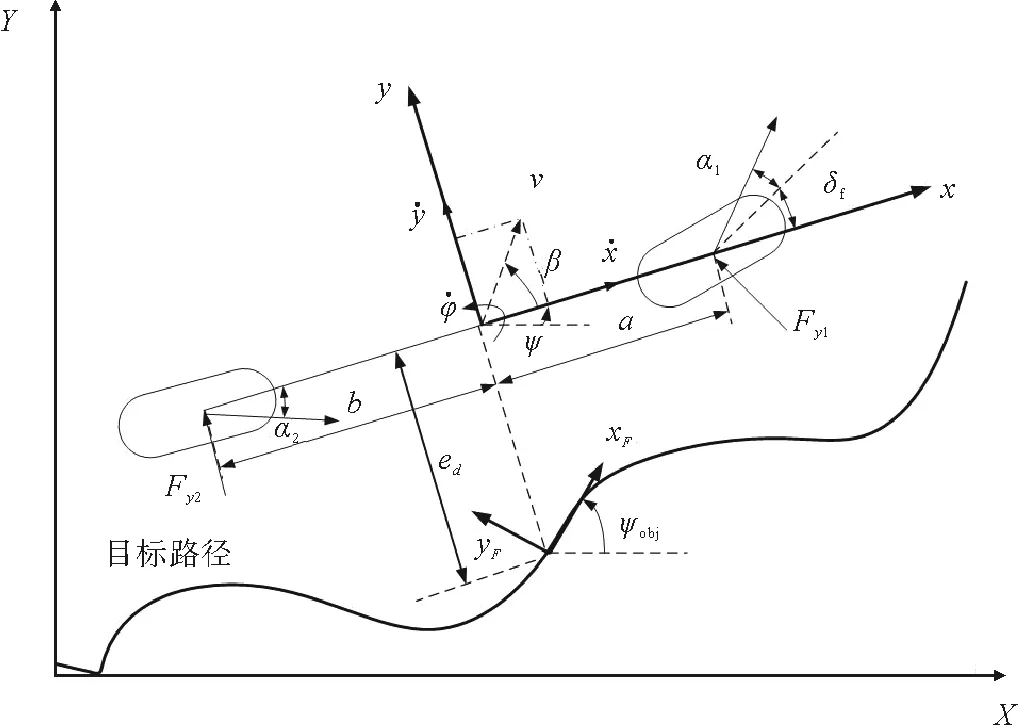
图1 二自由度车辆误差模型
根据图1建立的车辆动力学模型为
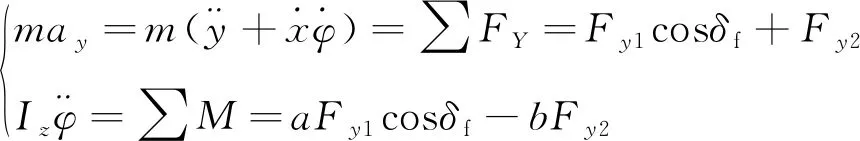
(1)
式中:m为整车质量;x,y分别为质心纵向、横向位移;δf为前轮转角;a,b分别为质心到前轴、后轴的距离;Fy1,Fy2分别为前、后轮胎侧偏力;φ为横摆角;Iz为绕z轴的转动惯量;M为横摆力矩。
此时轮胎可以线性表示:
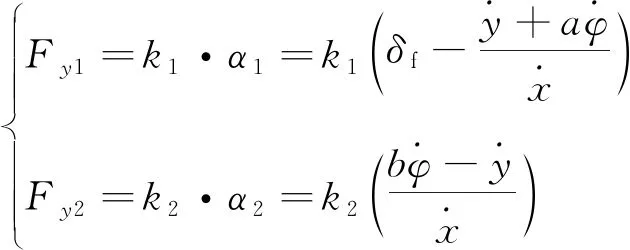
(2)
式中:k1,k2为前、后轮侧偏刚度;α1,α2为前、后轮侧偏角。
考虑到模型中前轮转角较小,因此cosδf≈1,故二自由度车辆动力学模型可表示为
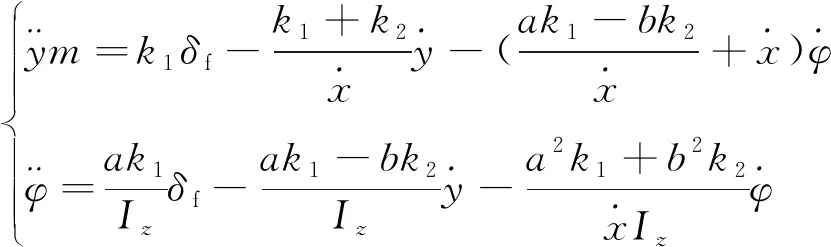
(3)
如图1所示,智能车辆在进行目标路径跟踪控制时,主要涉及到横向误差ed和航向角误差eψ。其中航向角误差:
eψ=ψ-ψobj
(4)
横向距离误差:
ed=vycos(ψ-ψobj)+vxsin(ψ-ψobj)
(5)
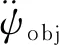
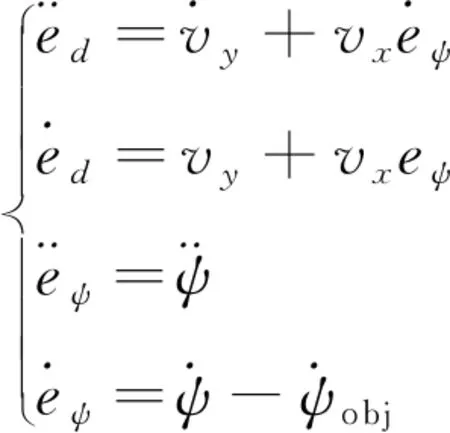
(6)
将式(4)(5)改写为状态空间方程:
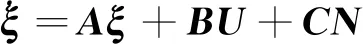
(7)
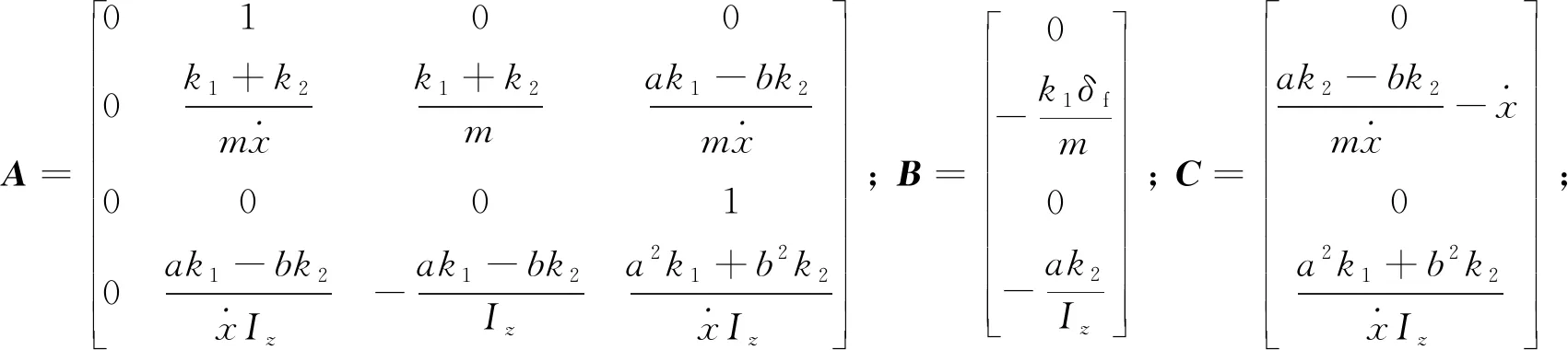
2 LQR控制器设计
采用LQR控制器[7-8],通过系统状态量反馈来实现车辆横向闭环最优控制。目标函数定义如下:
(8)
加入拉格朗日乘子,同时引入终端状态:
(9)
其中N≥k,构造Hamilton函数:
(10)
联立式(9)(10),求导并取极值得到LQR控制器的控制律为
U=-R-1BTλk+1=-R-1BTPk+1ξk
(11)
构造Riccati方程:
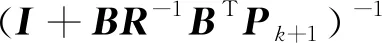
(12)
Pk+1是上述Riccati方程的解,因此求解LQR控制器增益:
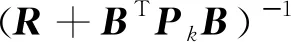
(13)
因此,LQR控制反馈控制律:
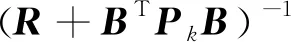
(14)
3 自适应预瞄前馈控制器
考虑到在车辆进行路径跟踪时,目标路径的变化是不可控的,且具有频繁变化的特点,因此引入前馈控制器,基于当前路径信息进行初步调节,结合LQR控制器及时且精准地对车辆进行控制。
自适应预瞄前馈控制器的原理如图2所示。规划路径拟合模块选取实际跟踪路径点拟合虚拟跟踪路径多项式。自适应预瞄模块根据拟合多项式曲率和相对航向角,并结合被控车辆信息给出预瞄距离,得到前馈道路曲率,最后代入至前馈转角公式得到前馈前轮转角并输入至被控车辆。
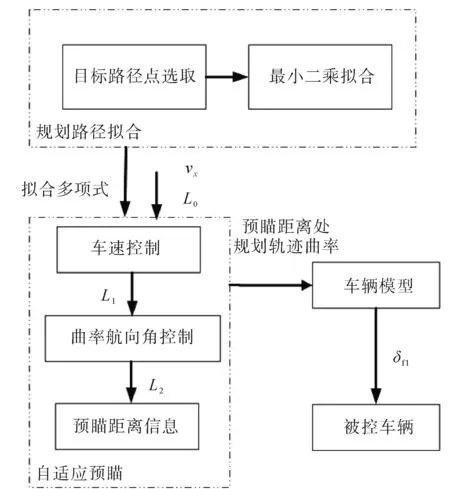
图2 自适应预瞄前馈控制器原理
3.1 规划路径拟合
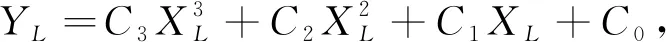
选取拟合点A,B,C,D。A点取原点(0,0),代表车辆当前位置。B点为车辆上一控制周期下的拟合曲率κlast,预设距离参数d1,则B点处的坐标:
C点根据预设距离dR计算,表示车辆在行驶过dR距离后,车辆轨迹大致收敛至目标轨迹。则C点处的坐标:
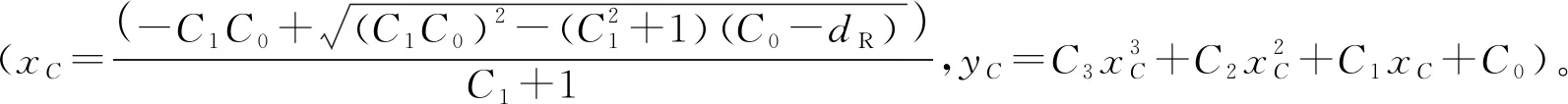
D点设定距离参数d2,为防止拟合轨迹发生震荡,因此C点沿着目标轨迹在y=0点处的切线上延伸d2的一个点,则D点处坐标:
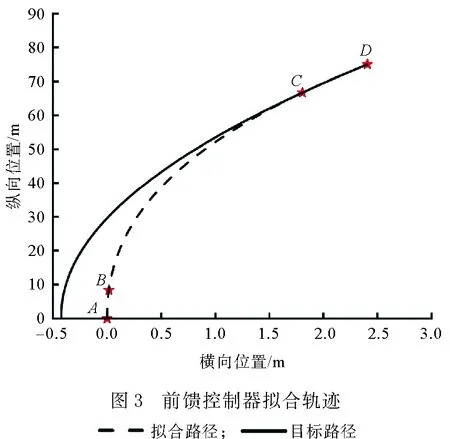
采用最小二乘拟合法拟合三次多项式,最终可以得到拟合轨迹,如图3所示。
拟合轨迹的目标多项式为
Y=a3X3+a2X2+a1X+a0
(15)
其中多项式可表示拟合路径的曲率为
κ=yplan1(x)=6a3x+2a2
(16)
拟合路径的相对航向角为
ψ1=yplan2(x)=3a3x2+2a2x+a1
(17)
3.2 自适应预瞄
在车辆的前馈控制中,预瞄点处的路径信息决定了前馈控制的控制性能,因此预瞄距离[9-11]成为影响路径跟踪效果的关键参数之一。若预瞄距离过小,前馈控制器就会失效,车辆容易在路径两侧摆动,导致车辆失去稳定性;若预瞄距离过大,车辆的跟踪路径横向偏差会变大,在道路变化频繁且变化幅度较大的工况下,容易导致车辆失控。
本文基于被控车辆的当前车速、规划路径曲率和规划路径相对航向偏差提出了一种自适应预瞄算法,原理如图4所示。
1) 车速控制模块。车速控制模块根据被控车辆当前车速vx、预设初始预瞄距离L0和预瞄距离的最大值Lmax、最小值Lmin得到预瞄距离L1。如图4所示,Lmax取值为20 m,Lmin取值为0.3 m,L0取值为3 m。
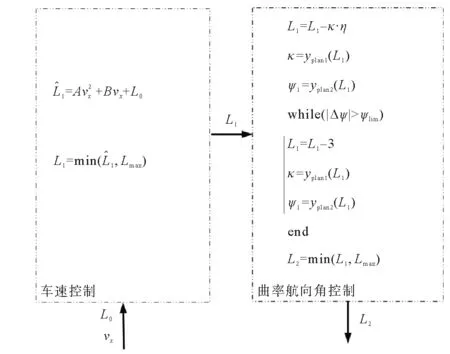
图4 自适应预瞄算法原理
预瞄距离与车速的二次函数形式如下:
(18)
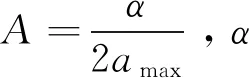
因此,预瞄距离与车速的二次函数可表示为
(19)
2) 曲率航向角控制模块。曲率航向角控制模块是根据车速控制模块所求预瞄距离L1代入式(16)求得规划轨迹在该点处的曲率,基于该点曲率对原先预瞄距离进行更新,其中选取的距离系数η=150。
为保证车辆前馈控制转角能够精准地对道路变化做出反映,设置一个预设航向角偏差[14]阈值ψlim=0.3,以此来判断更新后的预瞄距离。绝对航向角偏差Δψ为
Δψ=ψ1-ψ0
(20)
式中:ψ1为规划路径预瞄点处相对航向角偏差;ψ0为被控车辆规划路径当前位置处航向角偏差。
简化后的前馈转角公式为
(21)
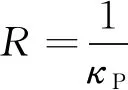
将规划轨迹预瞄点处曲率κP代入式(21)可得到车轮的前馈转角δf1。
因此自适应预瞄前馈LQR控制器的最终控制律为
U=-Kξ+δf1
(22)
4 试验与结果分析
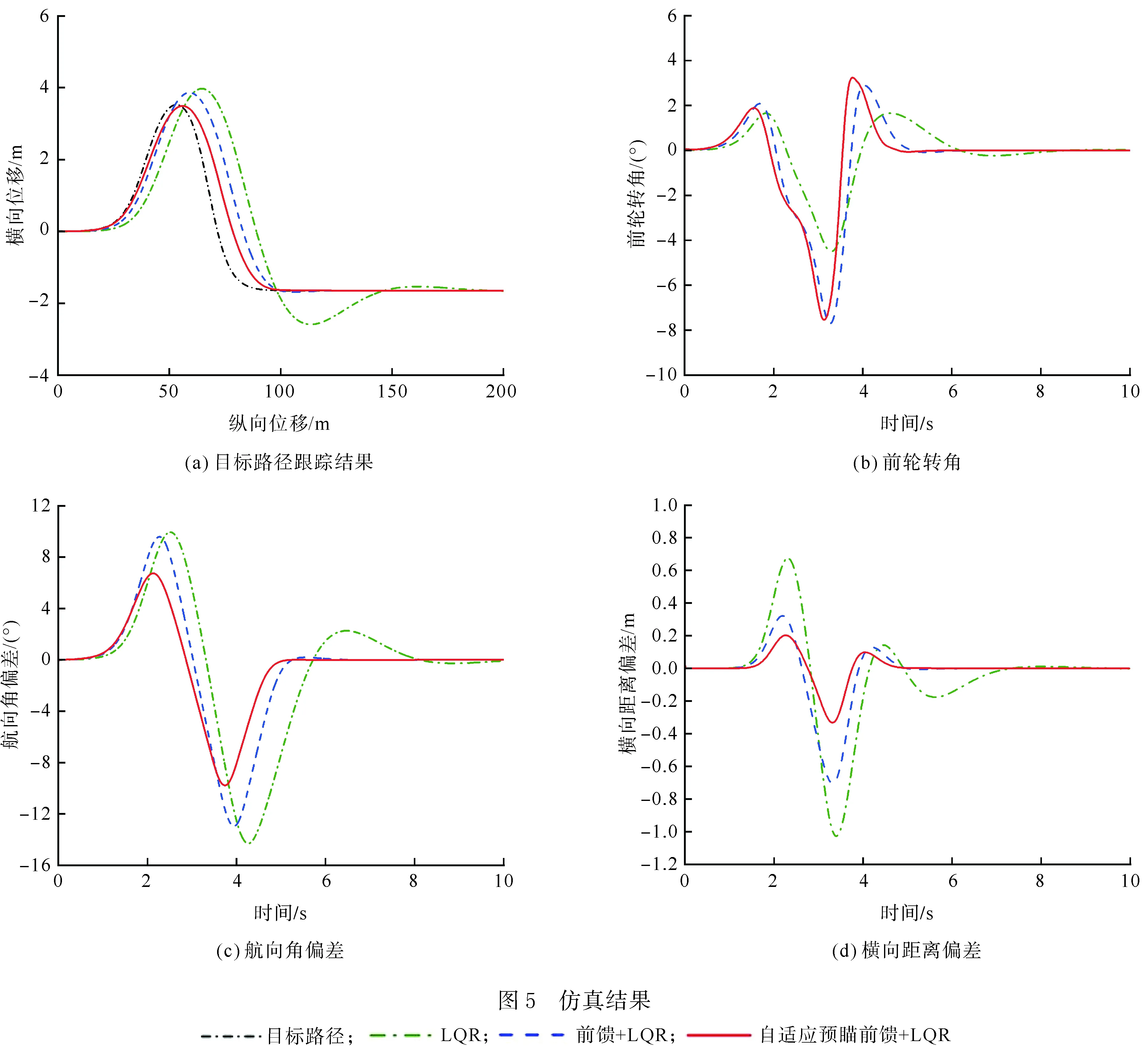
为了验证自适应预瞄前馈LQR控制器的有效性,利用Carsim-Simulink联合仿真对控制器的路径跟踪能力进行了测试。其中在Carsim中选择A级乘用车模型,车辆主要参数见表1。使用Carsim自带的速度控制器对车辆进行纵向控制,保证车辆按照车速设定值匀速行驶,车辆的纵向控制由Matlab/Simulink中编写的控制器计算前轮转角进行控制。测试工况选择了双移线测试工况[15],同时加入前馈LQR控制器作为对比,其使用单点预瞄方法,预瞄距离选为1.5 m。设定车辆车速为72 km/h,设置路面附着系数为0.85,仿真结果如图5所示。
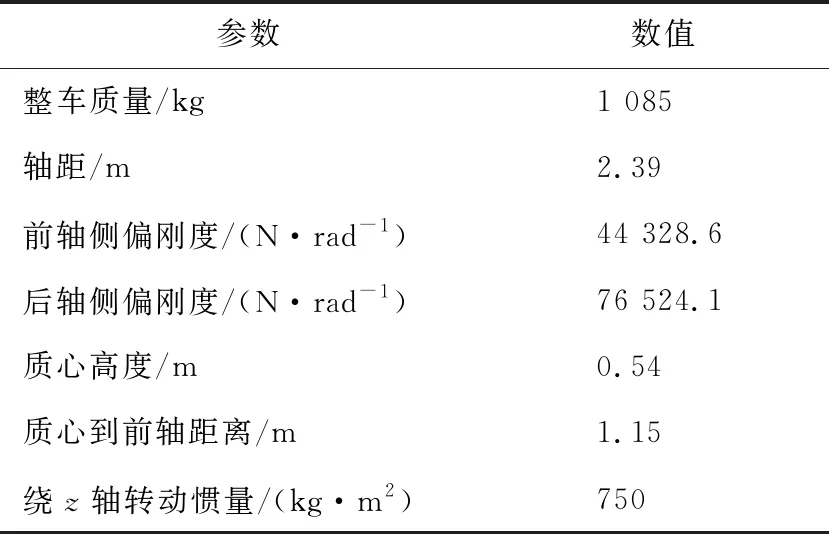
表1 试验车辆参数
由图5(a)可以看出,3种控制器路径跟踪效果中,自适应预瞄前馈LQR控制器路径与目标路径之间更加接近,单LQR控制器路径与目标路径之间差别最大。由图5(b)可以看出,为了保证跟踪效果,自适应预瞄前馈LQR控制器输出的前轮转角调整更多且幅度更大,前馈LQR控制器次之,单LQR控制器调整最少。
双移线工况下3种控制器的横向距离偏差和航向角偏差的绝对值最大值,绝对值均值见表2。由图5(c)(d)和表2可以看出:带有自适应预瞄前馈LQR控制器可以将横向距离偏差控制在0.332 m以内,且测试工况全程平均横向距离偏差为0.039 m,航向角偏差控制在9.779°(0.043 rad)以内,平均航向偏差为1.735°(0.009 rad);带有单点预瞄的前馈LQR控制器航向角偏差略小于带有自适应预瞄前馈LQR控制器,但其最大横向距离偏差达到了0.703 m,平均横向距离偏差更是达到了带有自适应预瞄前馈LQR控制器的2倍以上;未带前馈控制的单LQR控制器在三者中控制效果最差。

表2 三种控制器双移线测试工况偏差数据
综上所述,在双移线测试工况中,带有自适应预瞄前馈LQR控制器的路径跟踪性能最好;带有单点预瞄前馈LQR控制器性能次之;未带前馈控制单LQR控制器性能最差。
5 结论
本文设计的控制器在规定的测试工况下,相较于单点预瞄前馈LQR控制器和单LQR控制器,效果较好,其最大横向距离偏差控制在0.332 m以内,平均横向距离偏差为0.039 m,最大航向角偏差控制在9.779°(0.043 rad)以内,平均航向偏差为1.735°(0.009 rad),能够满足车辆路径跟踪中的跟踪精度和稳定性。
在后续的工作中,将进一步研究自适应预瞄前馈LQR控制器对车辆跟踪控制效果及稳定性的影响,并且进一步优化自适应预瞄算法逻辑,同时将控制器应用于其他工况并做进一步测试。

