伯努利多丢包的网络控制系统量化H∞滤波

马运强，甘 泉

(安徽机电职业技术学院 电气工程学院，芜湖 241000)

利用网络通信代替控制系统线路点对点连接，将控制器、传感器与被控对象连接而构建的控制系统，简称网络控制系统[1-3]。基于网络技术实现数据传输的网络控制系统具有低成本高性能等特点，受到了人们的青睐。然而网络信道资源有限，大量的网络数据通过有限信道传输占用大量的网络带宽资源，降低控制系统的稳定性[4-5]。同时网络数据在传输中易发生数据包丢失及时滞等现象，导致测量数据不准确[6]。

近年来，关于网络丢包问题人们给出了大量的解决对策。张瑞金等[7]考虑丢包和时延的网络，将控制系统变换Delta算子方程，利用伯努利序列刻画两侧丢包问题，通过随机马尔科夫过程建立李雅普诺夫函数。HUANG等[8]研究一类随机丢包的基因调控网络控制系统，利用开关基因调控网络方法处理系统模态信息丢失过程，设计了一种依赖混合H∞/l2-l∞的算法。LI等[9]探究含有数据丢失的网络控制系统H∞滤波，将闭环系统转化为马尔可夫跳跃系统，通过线性矩阵不等式推导系统满足均方稳定的不等式判据。LIN等[10]引入Bernoulli函数构筑网络数据传输丢包方程，借助T-S模糊技术设计的控制器保证了系统的稳定性。本文将分析多通道网络控制系统存在丢包及量化等问题，使用对数量化器量化网络数据，降低网络资源消耗，将多通道丢包构筑为伯努利变量。

1 问题描述

分析如图1描述的多通道丢包量化数据传输结构，系统方程Σ为

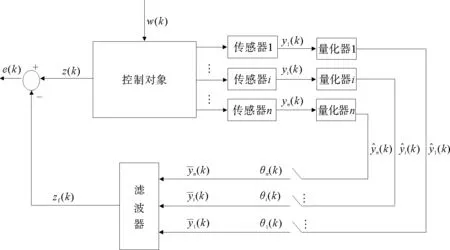
图1 丢包量化数据传输结构

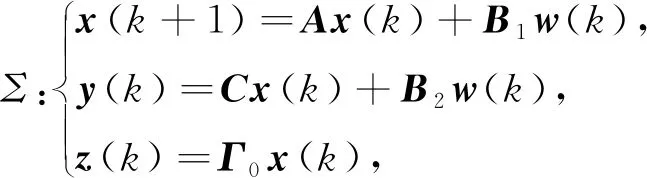
(1)

式中：x(k)∈Rm为系统的状态向量；y(k)∈Rn为系统的测量向量；z(k)∈Rp为系统的估计信号；w(k)∈l2[0,∞)为能量有界的扰动信号；A，B1，B2，C和Γ0为具有相宜维数已知矩阵。

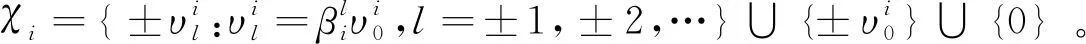
(2)

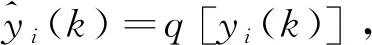
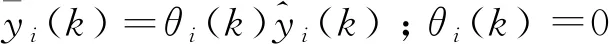
(3)

结合所述滤波器节点输入为

(4)

设离散滤波器F如下：

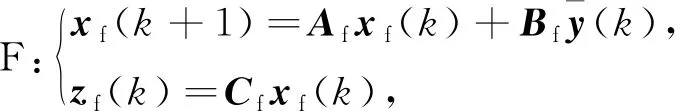
(5)

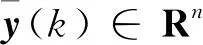
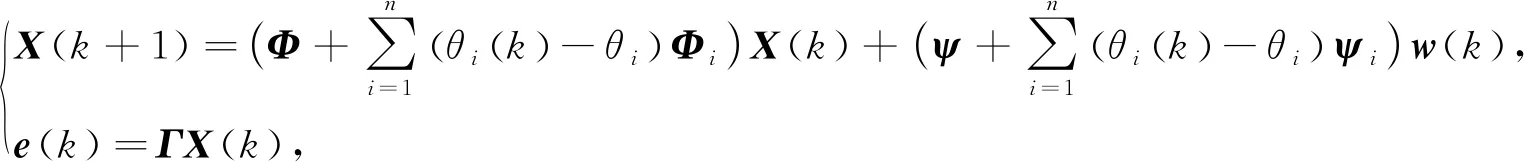
(6)

其中，

所阐述的H∞滤波目标是使得离散滤波器满足以下要求：

①在扰动信号w(k)=0情况下，若式(7)成立，

(7)

那么，滤波误差系统是随机稳定的。

②在扰动信号w(k)∈l2[0,∞)和零初始状态情况下，对于随机正数γ，若式(8)成立，

(8)

那么，滤波误差系统满足H∞性能指标。

2 滤波性能分析

定理1考虑网络控制系统，对于随机的正数γ，正定矩阵P，若式(9)成立，

(9)

那么，存在一类满足随机稳定及H∞性能的滤波误差系统。

证明：

1) 在w(k)=0情况下，令Lyapunov函数为V(k)，证明滤波误差系统的稳定性。

V(k)=X(k)TPX(k),

(10)

那么，将式(9)作差分取期望得

(11)

(12)

从而：

(13)

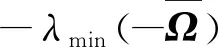
(14)

2) 在w(k)∈l2[0,∞)和零初始状态情况下，证明所提出的滤波器使得滤波误差系统满足H∞性能。

J(k)=E{e(k)Te(k)-γ2w(k)Tw(k)}≤E{e(k)Te(k)-γ2w(k)Tw(k)+ΔV(k)}

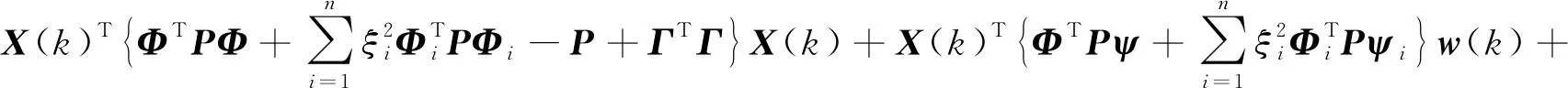
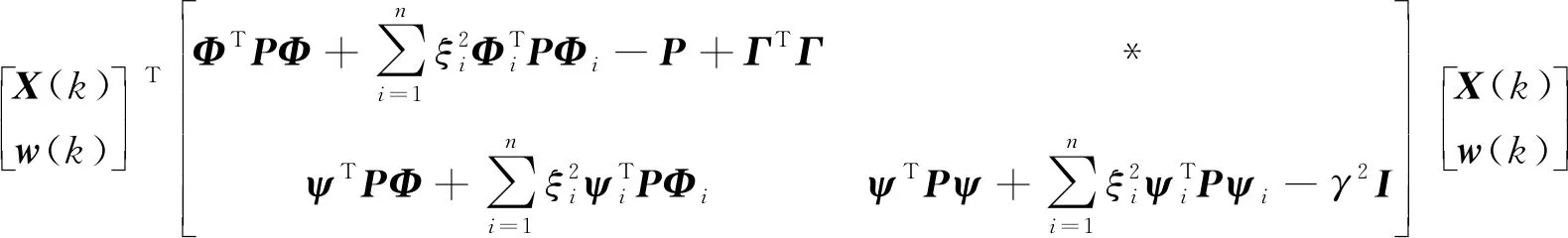
(15)

若定理1成立，那么式(9)隐含Ω，则J(k)<0，即

ΔV(k)+e(k)Te(k)-γ2w(k)Tw(k)<0,

(16)

对式(16)累加得

(17)

3 滤波器设计

定理2考虑网络控制系统，对于随机的正数γ，相宜维数的正定矩阵P和矩阵J，U，V和W，若不等式(18)成立，

(18)

其中，

那么，滤波器系数矩阵为

(19)

证明：Φ，ψ等项隐含不确定项Δ(k)，需分块处理，消除耦合联系。

(20)

其中，

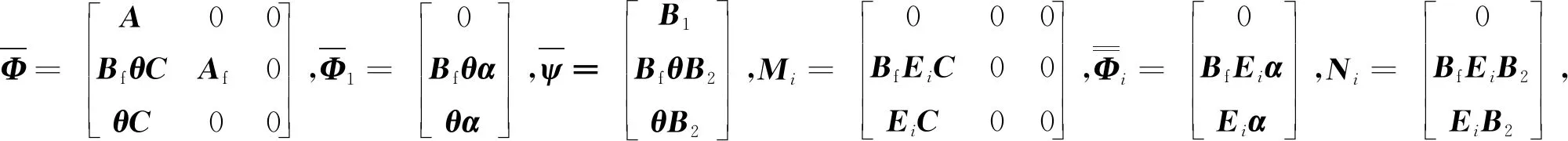
将上式代入式(9)得

(21)

利用Schur补引理式(21)化简为

(22)

式(22)中非线性变量-P-1，直接利用LMI运算复杂，引入矩阵J

(23)

(24)

其中，

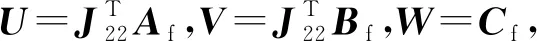
备注：H∞滤波器的最优性能指标γ*，利用LMI计算凸优化问题。

minμsubject to (18) withμ=γ2,

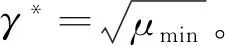
4 仿真示例

分析如下离散时不变系统。

设外部扰动信号w(k)=2e-0.5ksin(0.5πk)，γ*=1，量化器密度β1=β2=0.6，计算α1=α2=0.25，通道1和2的数据发送未丢包率为θ1=0.9,θ2=0.8，得方差ξ1=0.3,ξ2=0.4。根据定理2和Matlab LMI求解H∞滤波器系数。

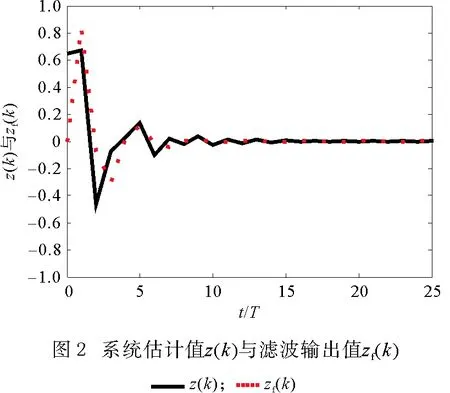
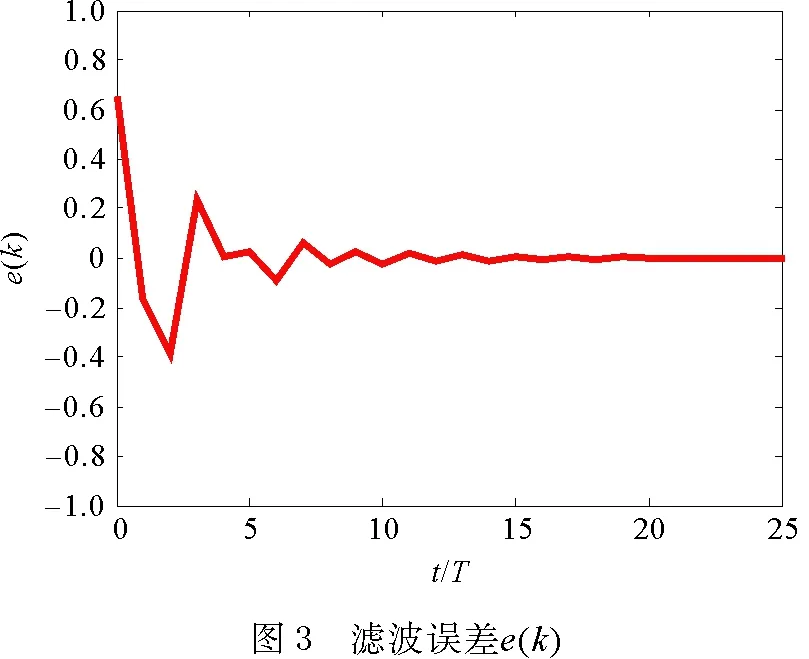
令控制系统的初始状态x(0)=[0.5 -0.5]T，滤波器系统的初始状态xf(0)=[0 0]T，控制系统估计值z(k)与滤波输出值zf(k)输出响应如图2所示，横坐标为离散采样时间，其中，T为离散采样周期。根据图2可知，在外部扰动信号作用下，10T之前滤波器输出值zf(k)与系统估计值z(k)局部存在差值，10T之后差值逐渐变小，并趋近吻合。因此，所设计滤波器可以较好地估计系统的真实值，抑制干扰信号。图3为滤波误差e(k)输出响应，可知滤波误差e(k)伴随采样时间的递增收敛为零。

5 结论

引入对数量化器减弱传输数据能量的损耗，使用伯努利序列降低数据包丢失对系统产生的不利影响。通过LMI技术定量给出量化密度、丢包率方差与抑制扰动性能指标之间联系。最后，通过数值示例证实H∞滤波器的有效性。此外，多通道丢包非线性系统量化问题为下一阶段探究目标。