基于CEEMDAN-ABC-LSTM组合模型的短时交通流预测
沈富鑫,邴其春,*,张伟健,胡嫣然,高 鹏
(1.青岛理工大学 机械与汽车工程学院,青岛 266525;2. 青岛市交通运输公共服务中心,青岛 266100)
随着汽车保有量的增加以及人们对交通要求的不断提高,交通拥堵、交通污染等问题正在严重影响着城市居民日常生活品质和出行时间。精准的短时交通流预测信息不仅可以帮助人们选择合适的交通工具、缩短出行时间,而且也是实现主动交通管制的关键。国内外专家、学者经过近几十年的研究构建出了一些预测模型,主要包括时间序列模型、卡尔曼滤波模型、支持向量回归模型和组合模型[1-4]。
近年来,由于科学技术和计算机技术的进步,以数据驱动和深度学习的短时交通流预测方法受到了广泛关注。数据处理方法通常用数据分解方法来提取交通流的特征,然后用神经网络模型进行预测。例如,WEI等[5]在研究中将经验模态分解(Empirical Mode Decomposition,EMD)和BP神经网络原理结合,并证实了方法的有效性。谭满春等[6]首先运用小波变换降低原始交通流数据中心的噪声,然后构建了基于去噪数据集和混合交通流预测模型。张阳等[7]提出了小波包分析和LSTM神经网络组合的交通流预测方法。YANG等[8]提出了一种基于EMD和叠加自动编码模型的混合交通流多步预测方法,并证实了预测的可靠性。陆文琦等[9]将原始速度序列利用集成经验模态分解算法进行分解,然后对分解后的序列进行处理,构建了行驶车辆速度预测模型。LI等[10]提出了集成经验模态分解和随机向量函数连接网络的行程时间预测模型,该模型在多项误差衡量指标方面均优于其他模型。谷远利等[11]利用基于信息熵的灰色关联分析提取空间特征变量,并用LSTM神经网络和门限递归单元神经网络组合预测不同时段车道的速度;王祥雪等[12]对深度学习理论进行研究,构建了LSTM-RNN的城市快速路交通预测模型,经过验证该预测算法的精确性、实用性和扩展性均有提高。RUI等[13]将LSTM和GRU组合模型运用到交通流预测领域并证实了其预测性能。POLSON等[14]提出了一种深度学习结构来预测交通流,并证明了深度学习结构能够捕捉非线性时空效应。朱永强等[15]将交通时间序列数据用互补集成经验模态分解(CEEMD)进行多尺度分解,构建了CEEMD-LSSVM组合预测模型,该模型的平均误差较小。
综上算法虽然在交通流预测方面取得了较好的预测效果,但仍有许多方面需改进完善。如在交通流数据分解方面,存在模态混叠、适应性和稳定性较差等缺点。为了能够获取更加稳定的交通流分解数据,减少交通流原始数据对预测结果产生的干扰,获取最佳模型参数值,本文提出了CEEMDAN-ABC-LSTM组合模型的短时交通流预测方法。
1 CEEMDAN理论
1.1 集成经验分解
经验模态分解(Empirical Mode Decomposition,EMD)由HUANG等[16]于1998年提出,它是一种自适应的分解方法,主要通过多次重复减去包络的均值来消除震荡。对于信号x(t),其经验模态分解算法由以下步骤组成:
1) 使用三次样条连接连续的局部最大值(各自的最小值)以导出上(或者下)包络线。
2) 通过对上下包络线求平均值,取得包络中值m(t)。
3) 从原始序列中减去上述已求得包络线的均值m(t)用以提取临时本地震荡h(t),得到h(t)=x(t)-m(t)。
4) 将得到的临时本地震荡h(t)多次重复计算步骤1)至3),直到满足算法条件要求,如此形成的h(t)就为分解后得到的一个固有模态函数(Intrinsic Mode Functions, IMF),记为c(t)。
5) 计算残余:r(t)=x(t)-c(t)。
6) 重复步骤1)至5)生成下一个IMF和残差。
因此,可以通过一个公式对原始信号x(t)进行重建:
(1)
式中:ci(t)与IMF一致(即本地震荡);rn(t)与第n个残差一致。
1.2 CEEMDAN算法
自适应噪声完全集成经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)是以EMD理论为基础,经过改进形成的一种新型自适应分解算法[17]。经过不断创新,它不但克服了EMD算法产生的模态混叠现象,还通过添加自适应白噪声对EEMD算法[18]进行改进,让重构后的信号误差降到最低。CEEMDAN算法实现步骤如下[19]:
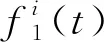
(2)
式中:ε0为在交通流序列中第一次添加白噪声幅度值的系数;ωi(t)为在交通流序列中添加的白噪声;N为交通流序列的长度。
2)可以得到第一个残余信号:
(3)
3)将残余信号r1(t)添加白噪声ε1E1ωi(t)继续分解,得到第二阶的IMF分量,记为
(4)
4)按照以上计算模式,可以得到第j个残余信号:
(5)
5)则第j+1阶的IMF分量为
(6)
6)对步骤4)和5)进行多次重复运算直到分解结束以获取最终的残余分量:
(7)
2 模型构建
2.1 LSTM原理
长短时记忆(Long Short-Term Memory,LSTM)神经网络,是由HOCHREITER等[20]首次提出的一种经过改进后的循环式神经网络,可以有效地缓解循环式神经网络所存在的梯度爆炸或者阶段性梯度消失的缺陷。LSTM主要由神经网络的输入层、隐含层、输出层三部分组成。与其他传统循环式神经网络不同的是,长短时记忆神经网络通过在隐含层结构上增加记忆模块,使信息达到较长一段时间的储存和遗传,结构如图1所示。
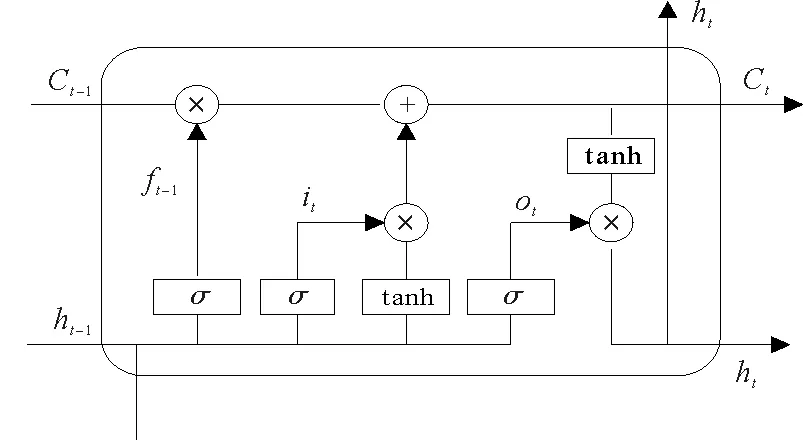
图1 长短时记忆网络结构
LSTM结构主要由遗忘门、输入门、输出门和记忆单元4部分构成,它也是一种链式结构,它们之间以一种特定的相互作用关系对信息进行过滤和保存。神经网络中的遗忘门主要对来自上一时刻单元状态的信息进行判断,决定哪些信息应该被保留,哪些信息应该被遗弃。由前一隐藏神经元节点ht-1和当前t时刻输入的信息xt经激活函数σ激活后,输出门限层ft,其过程可表示为
ft=σ(Wfxt+UfCt-1+bf)
(8)
输入门分别由sigmoid和tanh两个激活函数,准备更新接下来的记忆单元状态,其结构可表示为
it=σ(Wiht-1+Uixt+bi)
(9)
(10)
记忆单元状态更新中的Ct由过去长期状态和现在状态决定。其中过去长时间的刻画是由上一时刻单元状态Ct-1元素与遗忘门输出结果相乘体现,则Ct可表示为
(11)
输出门主要由短期记忆结合当前输入信息得到的信息ot和结合长期记忆最终输出的ht两部分构成,两者表示为
ot=σ(Woht-1+Uoxt+bo)
(12)
ht=ot*tanh(Ct)
(13)
式(8)—(13)中:σ为sigmoid函数;*为两个向量的乘积;Wf,Wi,Wo,Wc,Uf,Ui,Uo,Uc为训练过程中得到的权重矩阵;bf,bi,bo,bc为训练得到的偏移量。
2.2 基于人工蜂群算法的参数优化
在LSTM模型中,为了获取最佳隐含层神经元数量、分块尺寸、最大训练周期以及学习率,采用人工蜂群算法对模型参数进行优化。人工蜂群算法(Artificial Bee Colony,ABC)[21]主要是根据自然界中蜜蜂日常采蜜行为提出来的一种仿生和优化算法。它也是目前比较新颖的一种全局优化算法,其优化步骤如下:
步骤1:初始化模型参数,设定雇佣蜂数量SN,食物源的最大循环次数LM,最大迭代次数MC,以及LSTM模型的隐含层神经元数量nHU、分块尺寸mBS、最大训练周期mE和学习率LR,然后随机生成一个具有SN数量的初始种群。
步骤2:将均方根误差(RMSE)作为适应度函数对前SN个食物源的适应度进行训练。
步骤3:执行雇佣蜂和观察蜂阶段,限制参数寻优的范围。
步骤4:侦察蜂阶段,将相对较差的食物源丢弃获取一个新的食物源。
步骤5: 对给定的结束条件进行判断,如满足该算法的结束终止条件,则可以输出模型参数为最优解;反之,返回步骤3直到满足条件。
人工蜂群算法优化流程如图2所示。
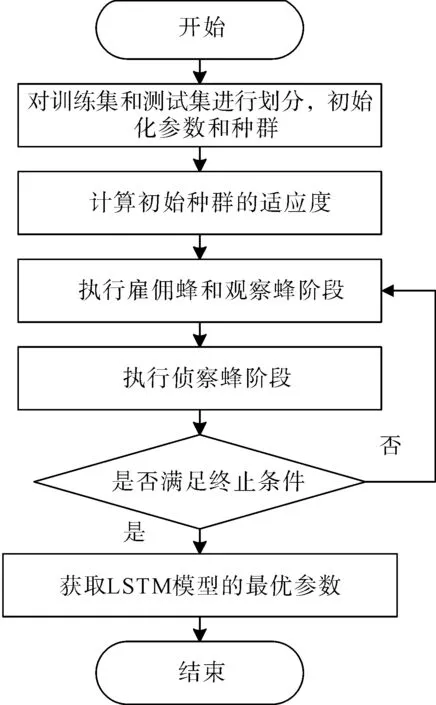
图2 人工蜂群算法参数寻优流程
2.3 CEEMDAN-ABC-LSTM模型构建
在交通流预测建模过程中,首先利用CEEMDAN算法将交通流时间序列分解成若干个不同尺度的IMF分量和一个残余分量,然后将分解数据输入到用ABC优化完成的LSTM神经网络中进行预测,具体流程如下:
步骤1:收集、整理实际获取到的交通流时间序列数据。
步骤2:将处理好的原始交通流数据用CEEMDAN算法进行分解,得到若干不同的模态分量IMF和一个残余分量R。
步骤3:对LSTM用人工蜂群算法进行参数优化,然后将分解后的模态分量和残余分量分别建立LSTM预测模型。
步骤4:将各分量数据进行训练预测,输出各分量的预测值。
步骤5:叠加每个模态分量的预测值,输出最终预测结果。
构建模型流程如图3所示。
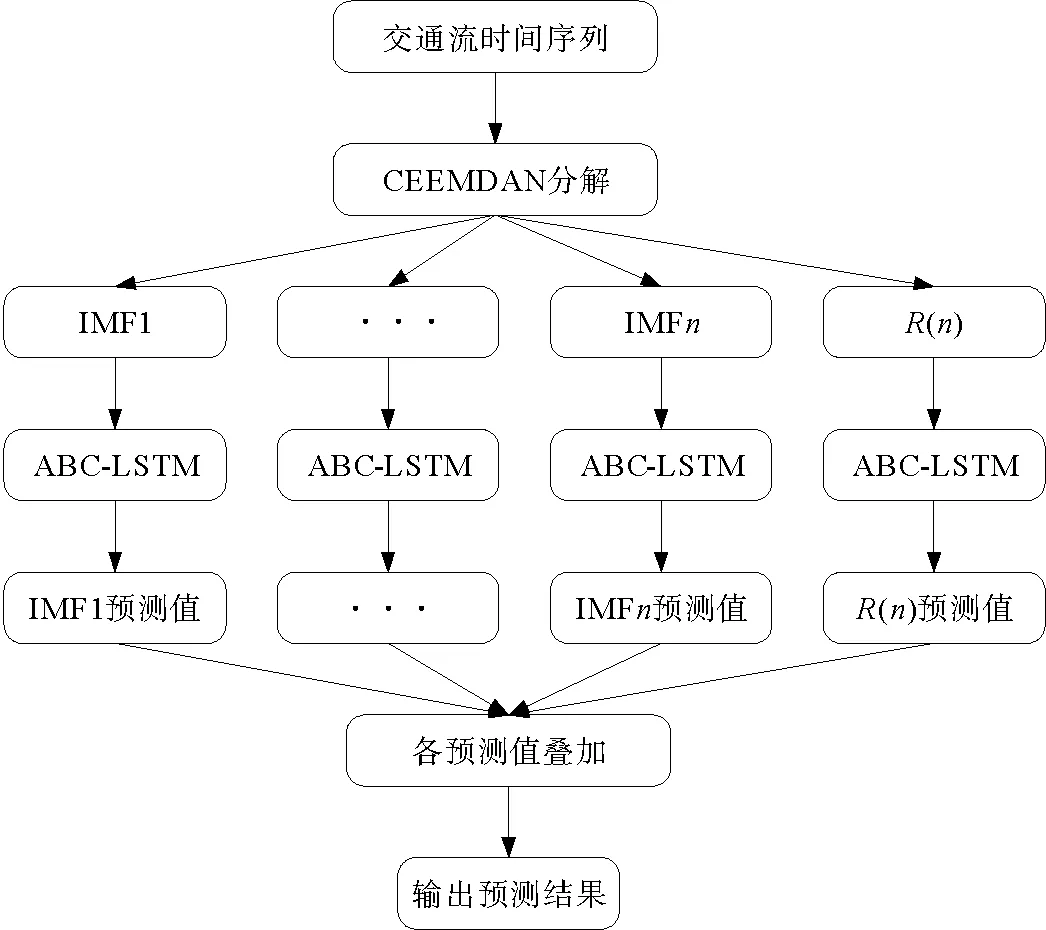
图3 CEEMDAN-ABC-LSTM模型预测流程
将模型的输入维数设置为6,数据训练和输出如图4所示。
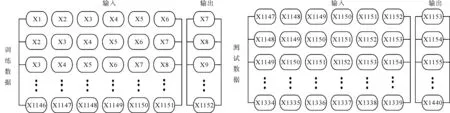
图4 数据的输入和输出格式
3 实例验证
3.1 数据来源
本文采集的数据来源于上海市南北高架路段感应线圈实测的交通流数据,数据采集的时间为2018年8月27日—8月31日。以每5 min一次的数据采集周期,共获取1440个实际交通流数据。交通流量随时间变化的折线如图5所示。
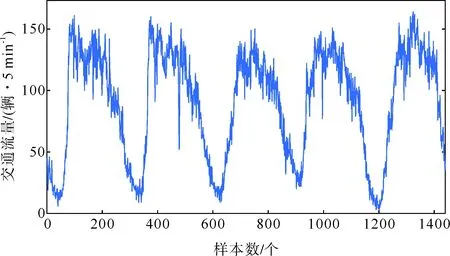
图5 连续5天交通流量数据
3.2 CEEMDAN算法分解
运用CEEMDAN算法对原始交通流时间序列数据进行分解。白噪声幅度值系数k设定为0.2,集成次数M设为500,根据算法的自适应分解性能,分解出10组不同尺度的IMF分量和1组残余分量,如图6所示。
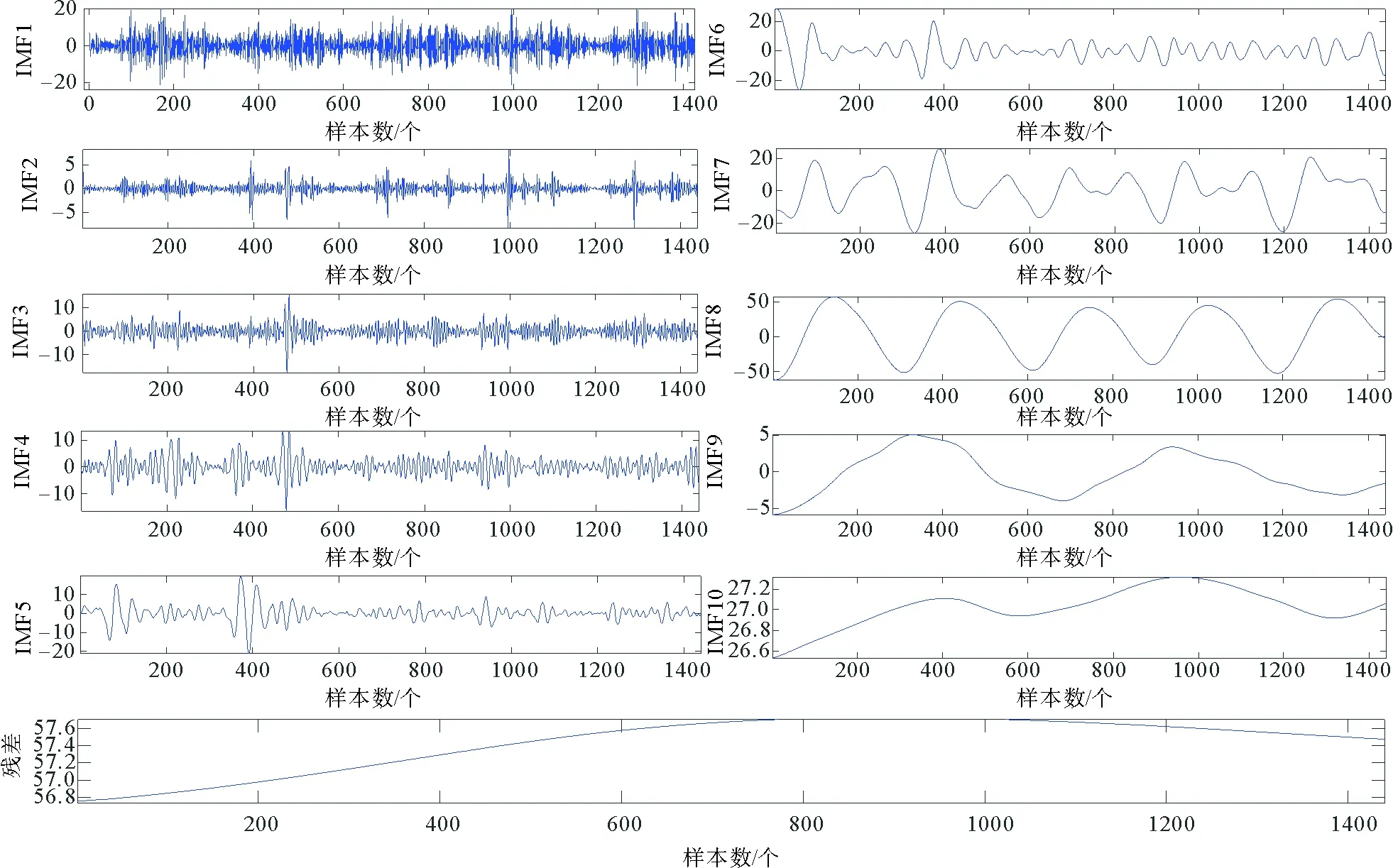
图6 CEEMDAN交通流时间序列分解
3.3 人工蜂群算法参数优化
采用人工蜂群算法(ABC)对LSTM的参数进行二次寻优。
ABC参数设定如下:雇佣蜂数量SN设定为50,食物源最大循环次数LM设定为100,最大迭代次数MC设定为200;将前4天的数据作为训练样本训练LSTM神经网络,为了方便表示,用RMSE表示人工蜂群算法参数寻优的过程。
建立模型的最优参数如下:LSTM隐含层神经元数量nHU为240,分块尺寸mBS为50,最大训练周期mE为250,学习率LR为0.005。寻优结果如图7所示。
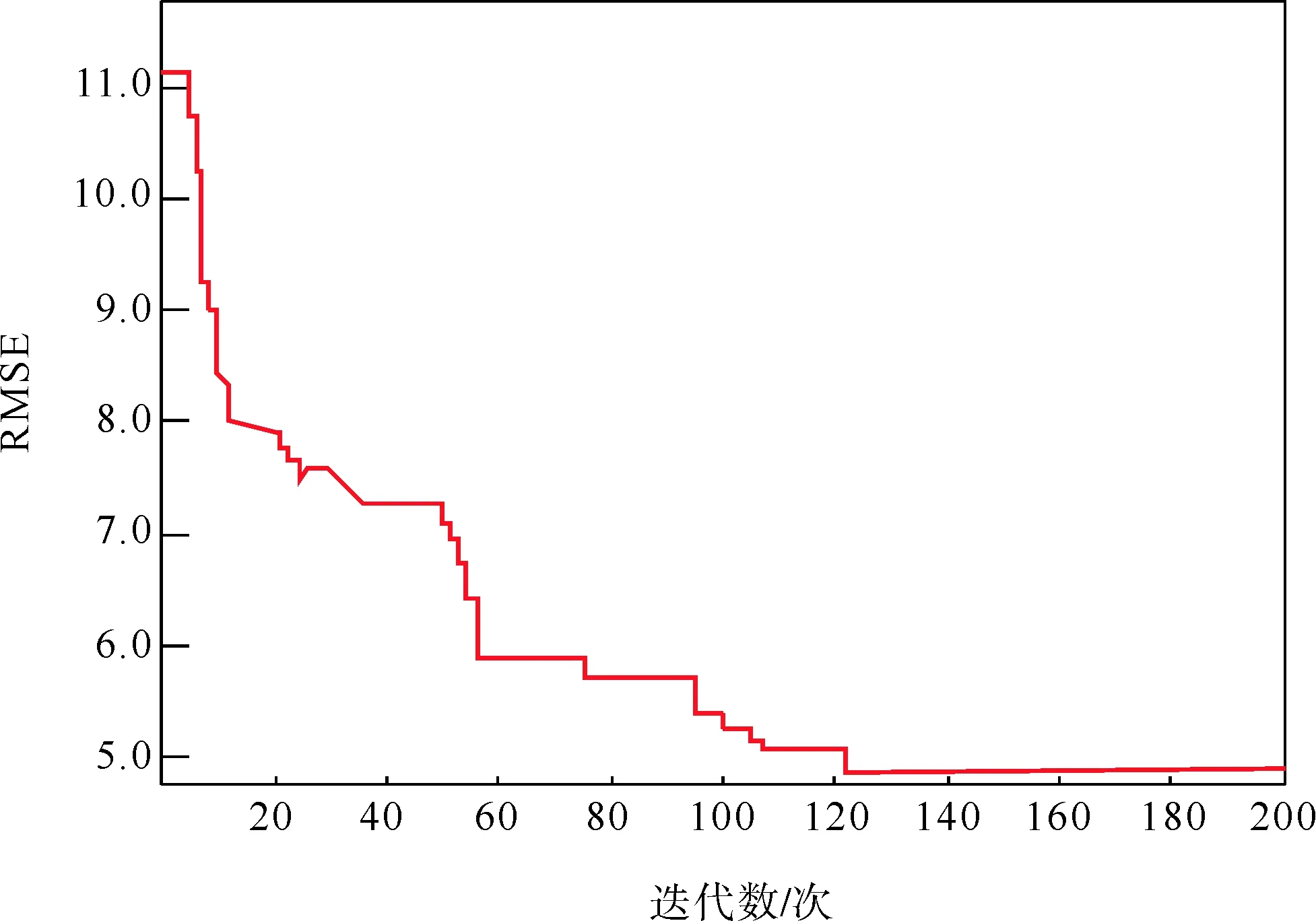
图7 人工蜂群算法参数寻优的过程
3.4 实验结果
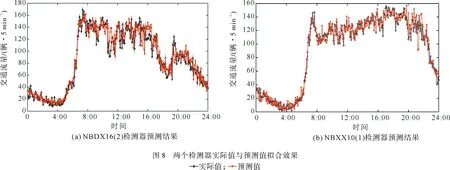
为了验证所构建模型在短时交通流预测方面的精度,将NBDX16(2)和NBXX10(1)检测器前4天采集的数据作为前期训练样本,用第5天实测数据作为测试样本进行对比分析,其中NBDX,NBXX分别为南北高架东线、南北高架西线;16,10为检测断面编号;2,1为车道编号。实验训练所用的电脑配置为i7-9750HQ处理器,运行内存16 G。图8为实测值与预测值的拟合效果,从图中可以看出,本文构建的组合模型预测结果与实测数据相比具有较高的拟合度,证实了本文方法的有效性。
3.5 结果分析
选取LSTM,ABC-SVM,ABC-BPNN预测模型作为对比,模型参数设定如下:BPNN模型的隐层数为1,隐层神经元的个数为50,激励函数为Sigmoid函数; SVM模型的惩罚因子λ=32,核函数参数γ=0.5。采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)三个指标进行分析评价。
(14)
(15)
(16)
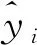
由表1、表2可以看出,本文方法的三个指标评价通过两个检测器验证都有较好的效果。MAE值分别为5.92和5.63,MAPE值分别为7.85%和7.57%,RMSE值分别为6.34和6.25,较其他三种方法的平均预测精度分别提升了19.8%,25.6%和38.7%,说明本文构建的CEEMDAN-ABC-LSTM模型具有一定的自适应能力和较高的稳定性,再次证实了本文所建模型的优越性。
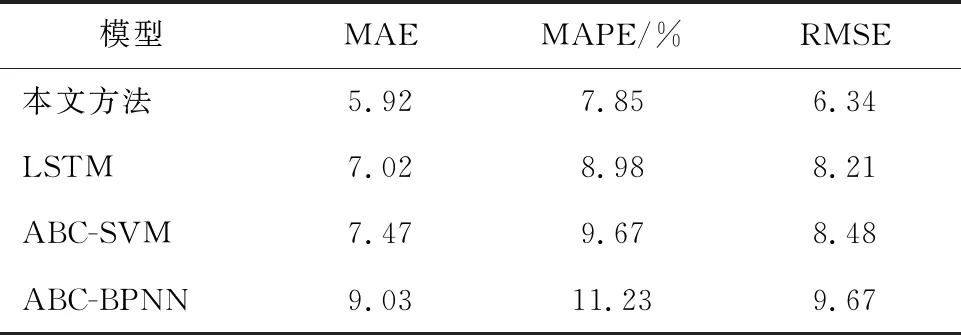
表1 NBDX16(2)检测器4种模型预测误差对比
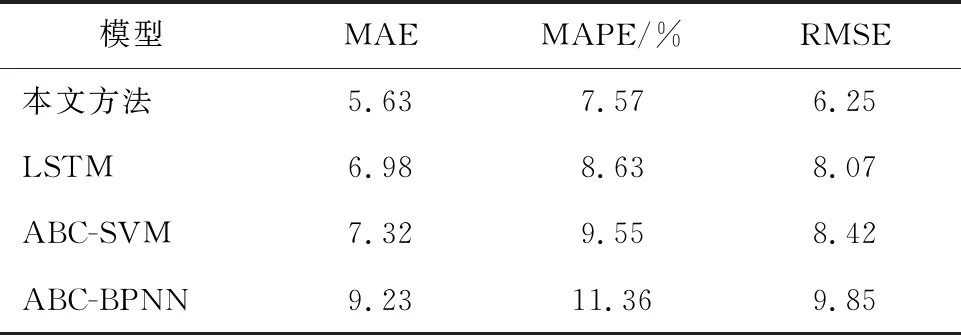
表2 NBXX10(1)检测器4种模型预测误差对比
4 结论
为了进一步提高短时交通流预测的精度,本文将非平稳、非线性交通流时间序列运用CEEMDAN算法分解为相对平稳的若干个不同模态分量,构建了CEEMDAN-ABC-LSTM组合交通流预测模型。通过实测数据验证,该模型表现出较好的预测性能,可以为以后交通流预测研究提供借鉴。但因现实交通系统较为复杂,受多种因素的干扰和影响,出行者也更加需要获取在出行时间范围内交通流的动态信息,因此单步的预测远不能满足人们出行要求,后续在本文基础上,对不同时间尺度下交通流的多步预测进行更深层次的研究。

