灰色预测：思想、方法与应用

谢乃明

（1.南京航空航天大学 灰色系统研究所，江苏 南京 211106；2.南京航空航天大学 经济与管理学院，江苏 南京 211106）

一、引言

预测是决策的基础，决策是预测的结果，较为准确的预测能够提高决策的科学性和有效性。系统预测是指根据现有系统或拟建系统的过去和现在发展规律，借助科学的方法和手段，对系统未来的发展进行估计和测定，形成科学的假设和判断。近年来，预测分析发展迅速，以预测分析为主体的数据挖掘技术变得炙手可热且愈发流行，这种现象的出现既有以大数据分析为基础的预测挖掘技术的推波助澜，更得益于人们对预测建模的深度理解。而预测分析的核心是针对不同的问题情景构建系统预测演化的数学模型或其他模型，因此，掌握系统演化规律和预测建模机理成为有效预测的关键。随着不同预测主题的深入研究，预测方法理论研究也逐步细分为统计与经济预测、贝叶斯预测、组合预测、数据驱动的预测等不同类型，预测方法应用研究也分成了供应链预测、金融预测、能源预测、环境预测、社会和人口预测等。［1］

由于系统内外扰动的客观存在和人们认识水平和能力的局限，人们在构建系统预测模型时所收集的信息常常带有某种不确定性，20世纪后半叶，包括模糊数学［2］、粗糙集［3］、灰色系统理论［4］等各种测度不确定性的新理论涌现，也不断和已有的系统预测思想相融合，形成了一系列系统预测新模型、新方法。灰色系统理论由中国学者邓聚龙教授所创立，其研究出发点是研究“部分信息已知、部分信息未知”的“少数据”“灰元信息”等贫信息不确定现象的系统，通过对系统的部分已知贫信息的挖掘、生成和建模，使得系统演化特征得以涌现，进而能够实现对系统进行科学评价、预测、决策和控制优化。灰色预测模型是灰色系统理论核心内容之一，其思想是通过特有的累加生成变换进行序列数据建模，把原始数据序列不明显的变化趋势通过累加变换后呈现明显的增长趋势，并用灰色差分方程和灰色微分方程对变换后的数据进行建模，最后用累减生成进行数据模拟和预测。

二、灰色预测建模的基本思想

根据文献检索，最早见诸报道的灰色预测模型提出于1984年，灰色系统理论创始人邓聚龙教授在对粮食长期预测中首次提出灰色动态模型［5］。依据邓聚龙教授最初的建模思想，灰色预测模型可以简单表达为定义1。

定义1

设原始时间数据序列为{xi(t1)，xi(t2)，…，，若为{xi(t1)，xi(t2)，…，xi(tn)}的累加生成序列，则

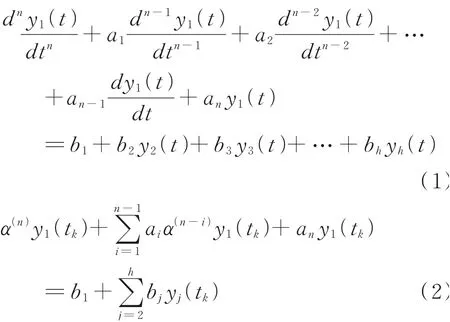
称为GM（n，h）模型，其中式（1）称为GM（n，h）模型的微分形式或连续形式，式（2）称为GM（n，h）模型的差分形式或离散形式，n代表微分或者差分的阶数，h代表模型变量个数。当n=1，h=1时，GM（n，h）模型变成GM（1，1）模型；当n=2，h=1时，GM（n，h）模 型 变 成GM（2，1）模 型；当n=1，h=N时，GM（n，h）模型变成GM（1，N）模型；以此类推。

根据邓聚龙教授对灰色预测模型的定义和内涵解析，灰色预测模型与其他预测方法相比有几个新的建模思想：一是不同于其他预测模型的直接数据建模，而是通过对数据序列的映射处理，为微分拟合建模提供中间信息；二是通过数据的序列生成弱化原始数据序列的随机性，尤其是对非平稳数据序列随机性的弱化；三是提出模块预测和累加生成思想进行建模。在此基础上采用微分拟合建模方法构建了灰色预测模型的上述通用形式GM（n，h）模型。其后，邓聚龙教授基于现实案例的总结提炼，针对灰色预测模型在社会经济应用案例进一步提炼了五步建模思想［6］。并根据灰色预测建模所面临的单变量情景和多变量情景分别细化为GM（1，1）模型和GM（1，N）模型。其中，序列生成是灰色预测模型与其他预测方法的重要区别之一，在实际问题建模过程中，考虑时间序列数据的随机性以及数据量的有限性，难以准确度量数据序列潜在的演化规律，邓聚龙教授提出建立时间序列数据的累加结构，即累加生成算子，通过序列的累加生成挖掘出序列的动态变动规律［7］，再根据累加生成后的数据进行建模，从而取得良好的模拟和预测效果。本质上，累加生成是对原始数据序列演化规律的挖掘，起到对系统演化的非参数可视化模式辨识作用；主要适用于系统演化规律相对稳定，且数据量有限导致系统规律可视化不明显情景，对于系统演化规律相对稳定数据量大的情景也可以取得较好的模拟和预测效果。对于系统演化规律不够稳定的情景，则需要对于数据序列进一步挖掘才能取得良好的建模效果，如系统演化过程加速增长、加速衰减及振荡变化等情景，采用常规性累加生成数据挖掘效果就不够好。针对这些复杂情景，刘思峰教授提出了缓冲算子的思想，包括强化缓冲算子和弱化缓冲算子，在深入研究缓冲算子性质与作用机理基础上，形成了包括平均弱化缓冲算子、加权平均弱化缓冲算子、分数阶平均弱化缓冲算子、分数阶加权平均弱化缓冲算子、平均强化缓冲算子，加权平均强化缓冲算子、分数阶平均强化缓冲算子、分数阶加权平均强化缓冲算子等在内的缓冲算子体系；通过运用缓冲算子对冲系统演化的冲击扰动干扰，还原了系统的演化规律，提高了预测效果，详细内容可见刘思峰教授的经典著作［8］，此处不再赘述。

灰色预测模型的建模过程与其他预测模型的建模过程基本一致，大致可以分成模型变量选择、原始数据收集与处理、建模数据序列生成、模型结构选择、背景值序列生成、模型参数求解、模型性质分析、数值模拟误差分析、预测应用等步骤（如图1所示）。但其中建模数据序列生成和背景值序列生成是灰色预测模型所独有，与其他预测模型不同。

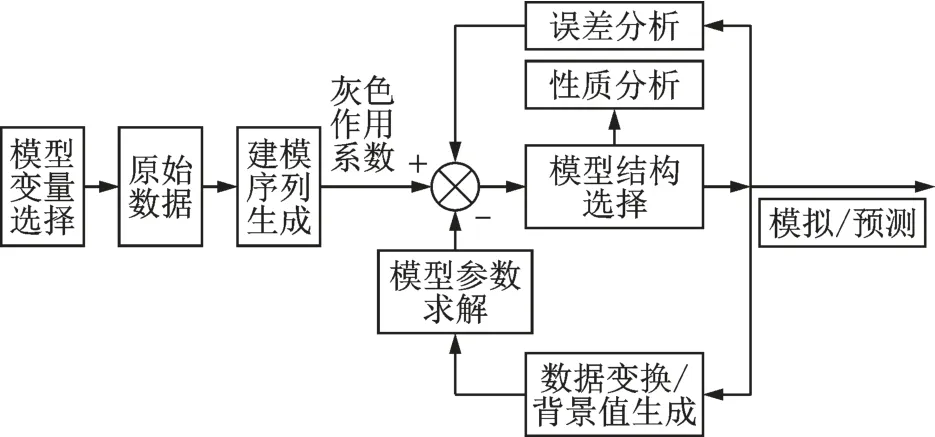
图1 灰色预测模型的一般步骤

以GM（1，1）模型为例，其建模步骤可以简单总结为以下几步：

步骤1：收集建模指标原始序列数据x={x(t1)，x(t2)，…，x(tn)}；

步骤2：计算建模序列生成数据y=

步骤4：结合模型离散形式x(tk)+ay(tk)=b或均值形式，运用最小二乘方法求解参数a和b的估计值；

步骤7：误差分析及预测。

三、灰色预测模型的主要分类

从定义1可以看出，经典的灰色预测模型既包括连续形式（式（1））也包括离散形式（式（2）），大量公开发表的论著表明灰色预测模型能够符合应用需求，取得较高的预测精度。然而，从理论研究的视角有时候还存在一些难以解释的现象，比如针对一些特殊案例也会出现模拟和预测误差很大的情况，对于不同类型模型的机理探讨不够，以及灰色预测模型体系框架还不够完善等等。针对灰色预测模型预测精度不稳定现象，作者从理论分析和实验分析视角进行深入探讨，发现问题存在的根本原因在于：尽管累加生成建模能够有效地发现数据变化趋势，但是由于灰色微分方程和灰色差分方程之间的变换存在着微小的近似误差。当所收集的数据增长率变化较小时，微分方程和差分方程互换所带来的模型误差往往比较小，并不显著影响预测模型的精度；然而，当所收集的数据增长率变化较大时，微分方程和差分方程互换所带来的模型误差就比较大，会影响到模型的预测效果，严重时甚至导致模型不可用。针对这一突出问题，作者在继承累加生成变换的基础上通过构建离散形式的灰色预测模型来解决误差问题，形成了离散灰色预测模型［9］。之后，陆续发展出近似非齐次指数序列离散灰色模型、多变量离散灰色模型、灰数序列离散灰色模型等灰色预测新模型［10-12］，2016年作者将系列离散灰色预测模型研究集结成册，出版了专著《离散灰色预测模型及其应用》［13］。

近年来，灰色预测模型取得了非常大的研究进展，绝大部分已构建的模型都是源于GM（1，1）模型或者GM（1，N）模型，后来根据模型形式是连续型、离散型以及变量个数是单变量、多变量的情形，分别派生成连续型单变量灰色预测模型、离散型单变量灰色预测模型、连续型多变量灰色预测模型、离散型多变量灰色预测模型。此外，还出现了一些非线性灰色预测模型、灰数序列预测模型等，形成了现有的灰色预测模型的基本分类体系（如图2所示）。

图2 新型灰色预测模型分类

连续型单变量灰色预测模型源于GM（1，1）模型，GM（1，1）模型的连续形式和离散形式分别为该 模 型 可以简单理解为是一种自回归模型，系统变量x(tk)只与自身的累积量y(tk)有关，而与其他变量无关，其中首项是针对时间序列的数据间间隔为1的情形下的特殊表达，当时间间隔不为1时该模型转变为非等间距GM（1，1）模型。经过30多年的发展，在该模型的基础上已经衍化发展出一系列新模型，这些模型的共性是保留了GM（1，1）模型的建模思路。主要思想是只考虑单一变量数据序列{x(t1)，x(t2)，…，x(tn)}及其累加形式来建模表征系统的演化规律，不考虑其他变量的影响，模型形式上既保留了微分形式也保留了差分形式，建模过程中用微分形式表征系统变量随时间的演化关系，而差分方程则主要用于模型参数的求解。其共性表达形式可以归纳为模型中和y(t)的关系保持不变，参数a（发展系数）用于表征系统的演化趋势。可见在这些衍生模型中对系统演化的发展趋势测度是保持不变的，变化的部分主要是剩余项b（作用量），从常数项逐步变化为和时间t相关的量b+f(t)，f(t)表达形式基本上属于类似多项式的线性关系，这些模型可以很好地表征近似非齐次增长、波动性增长等多种情景的系统演化特征［14-21］。特殊地，当f(tk)=b1tk时，模型变为近似非齐次指数增长的灰色预测模型。

离散型单变量灰色预测模型源于作者提出的DGM（1，1）模型［9］。该模型继承了灰色预测模型的累加生成建模思想，但舍弃了GM（1，1）模型微分方程形式而直接构造离散形式y(tk)=β1y(tk-1)+β2来表征系统演化规律，该离散形式可以等价转换为GM（1，1）模型的差分形式；该模型及其诸多衍生模型保留了y(tk)和β1y(tk-1)项，其中参数β1类似于GM（1，1）模型中的发展系数a，用于表征累加生成序列的迭代演化关系。当β1〉1时，表明系统演化趋势是增长的；当β1〈1时，表明系统演化趋势是衰减的。用β1来调节y(tk)和y(tk-1)差异契合了邓聚龙教授提出灰色预测模型时所陈述的差异信息思想。类似于GM（1，1）模型的衍生形式［22-34］，离散型单变量灰色预测模型变化的部分也是在常数项β2，将常数项变化为和序数k相关的量，其表达形式也类似多项式的线性关系，少量衍生模型还加入了三角函数等信息。这些模型也可以很好地表征近似非齐次增长、幂次变化以及波动性增长等多种情景的系统演化特征。

连续型多变量灰色预测模型源于GM（1，N）模型，模型形式上既保留了微分形式也保留了差分形式，建模过程中用微分形式表征系统变量随时间的演化关系，而差分方程则主要用于模型参数的求解。模型中和y(t)的关系保持不变，参数a（发展系数）用于表征系统的演化趋势，而作用量从GM（1，1）模型的b变为即考虑其他变量对于系统主变量的影响关系，影响形式是线性结构的，且影响变量也进行了累加生成，说明测度的是影响变量的累积性效果。与单变量灰色预测模型不同，连续型多变量灰色预测模型的众多衍生形式考虑了时滞效应的影响，即影响变量不一定与系统主变量同步变化，而是有一定的时间差，即滞后作用效果［35-47］。

离散型多变量灰色预测模型和离散型单变量灰色预测模型类似，继承了累加生成思想，并且采用离散形式直接建模，最早出现的离散型多变量灰色预测模型是DGM（1，N）模型以及离散型多变量灰色预测模型的通用形式DGM（r，h）模型；模型趋势性部分与连续型多变量灰色预测模型一样，保留了y1(tk)+β1y1(tk-1)的关系，用β1来调节y1(tk)和y1(tk-1)差异，表征系统主变量的自我演化关系，表示其他变量对于系统主变量的影响关系，影响形式是线性结构的，且影响变量也进行了累加生成，说明测度的是影响变量的累积性效果；部分衍生模型也考虑了时滞因素的影响［48-53］。

非线性灰色预测模型与前文所总结的4类模型不同，建模过程中只继承了累加生成建模思想，模型的形式上不是固定的，没有保留或y(tk)+β1y(tk-1)的单一线性演化关系，而是包括了y2(t)、yγ(t)等多种形式。迄今为止，非线性灰色预测模型还相对较少，仅限于Verhulst模型、Bernoulli模型、幂模型、Lokta-Volterra模型等少数几种形式，用于测度有极限的、波动的等演化趋势。比如Verhulst模型可以用来表示，Bernoulli模型可以用byγ(t)来表示。［54-59］

向量型灰色预测模型是对单变量、多变量灰色预测模型的进一步拓展，传统的灰色预测模型不管是单变量、多变量模型都是单输出的，而现实问题中常常出现多输入、多输出的系统。假设有xi={xi(t1)，xi(t2)，…，xi(tn)}，i=1，2，…，m的m个 输入变量，yi是xi的累加生成序列，基于该思想构架了形如模型，该式是一系列方程组成的方程组的矩阵形式，A代表变量之间的影响系数矩阵，B代表作用量的影响向量。与前文所述的其他类型的模型一样，作用量可以进行多种形式的拓展，特殊地，该模型也可以拓展到包含内生变量和外生变量的复杂形式［60-66］。

四、灰色预测模型的理论和应用进展

以上所述的模型分类及新模型构建的研究，极大丰富了灰色预测模型的方法体系，取得了较多研究进展。除此之外，还有大量文献聚焦于提升已有模型的模拟和预测精度，主要包括数据变换、背景值优化、参数优化和初值优化等方面。数据变换上主要是依赖于提高建模数据序列的光滑比、运用缓冲算子变换以及函数变换等形式提升建模精度。邓聚龙教授首先定义光滑比概念并以提升数据的光滑比来提高建模精度，后来李群、何斌等学者提出用对数变换、函数变换提升建模效果［67-70］。背景值是累加生成序列中y(tk)和y(tk-1)的加权值，用于表征时序从k-1到k的区间段的系统演化规律，起初简单用0.5和0.5来表示权重值，后来考虑数值偏差，提出了多种背景值优化的方法［71-73］。初值是灰色预测模型求解的初始条件，起初简单以x(t1)为初始值，后来考虑初值可能存在偏差，一些学者提出优化的设计思想，提出以终值x(tn)为初始条件，也有提出加一个调节项c，改为x(t1)+c，x(tk)+c和x(tn)+c等多种不同形式。参数优化是指针对灰色预测模型的参数a和b进行的优化求解，传统灰色预测模型都是以最小二乘方法求解参数值，有学者认为灰色预测模型中数据的规律并不一定符合最小二乘原理，因此提出目标规划、智能优化等多种方法对参数进行优化求解，取得了较好的改善效果。［74-75］

应用方面，灰色预测模型解决了大量社会经济预测、能源预测、交通流量预测、电力预测、工程预测等实际问题。能源预测是近年来最热门的领域，涌现了大量的论文，如Wang等使用混合ARIMA和非线性新陈代谢灰色模型预测美国页岩气月产量［76］。Zhao等提出了滚动机制优化的灰色模型Rolling-ALO-GM（1，1），用于优化年度电力负荷预测［77］。Shaikh等基于优化的非线性灰色模型预测中国的天然气需求［78］。Wu等通过参数优化和分数累积的概念，提出了FAGMO（1，1，k）来预测核能消耗［79］。Xiao等建立Riccati-Bernoulli微分方程，用改进的花授粉算法优化幂指数，并利用该模型对中国和印度的清洁能源消费进行了估算和预测［80］。Luo从Verhulst模型的白化方程Logistic方程出发，引入常系数Riccati方程对白化方程进行优化，建立了基于Riccati方程的灰色预测CCRGM（1，1）模型，利用模拟退火算法对非线性项进行了优化，预测了2019—2028年北美地区的核能和水力发电能耗［81］。这些论文将灰色预测模型与实际问题有机结合，得出了有价值的研究结论，并为能源政策制定等提供了有益的参考。此外，如Wang、Hipel和Wang提出NGBM（1，1）模型，并将参数优化方法表述为组合优化问题，应用该模型对2001—2011年中国31个省的工业废水年合格排放率进行了模拟和预测［82］。Ou将背景值优化、遗传算法和GM（1，1）模型相结合提出新的灰色预测模型，并将其应用于模拟1998—2010年我国台湾农业产量数据的年值，取得较 好 的 预 测 效果［83］。Intharathirat、Salam和Kumar采用多变量灰色模型预测发展中国家的城市固体废物量［84］。Evans提出估计广义灰色Verhulst模型参数优化方法，并以英国某钢材使用强度预测中加以应用，取得了较好的预测效果［85］。类似的应用也大量出现在交通流量预测、社会经济预测、工程应用等领域，此处不再赘述。

五、结束语

尽管灰色预测模型体系日益丰富，应用领域日益广泛，但灰色预测模型的理论体系还不够完善，还有较多问题值得深入研究。如灰色预测模型的建模适用条件和建模机理，即灰色预测模型区别于其他预测模型的独有特征还要深入研究；考虑灰信息的灰色预测模型构建及应用需要进一步研究；对于一些特殊情形，如具有增长阈值限制、具有波动性变动特征、具有竞争演化关系及结构演化关系等情形的灰色预测模型还可以深入研究。