授人以鱼不如授人以渔
——以微专题“面积法”为例
赵 军 (江苏省太仓市实验中学 215400)
1 基本情况
1.1 授课对象
学生来自平行班的初三年级,基础较好,知识结构完整,有一定的推理能力和解决问题的能力.
1.2 教材分析
在迎接中考的复习阶段,我们以苏科版《义务教育教科书(数学)》为蓝本,将数学知识与解题方法融合,通过重新建构,以微专题的形式进行深入而又高效的复习,以期在学习方法、解题技巧等方面达到深度学习的目的.
“微专题”顾名思义就是小专题,是围绕一两个紧密相关的知识或思想方法而形成的专题研究,它可以单独研究某一知识体系、某个数学思想或某种解题策略.微专题的设计应当结合学生的学情,从学生已有知识、能力出发进行研究,具有入口小、针对性强等特点.在教学实践过程中要做到科学引领,精准施策,体现以小见大、见微知著的特点.“面积法”是一种常见的解题方法,它通常以某个图形为载体,通过两次计算其面积,构造方程解决问题.面积法的适用面广而又分散,具有灵活而又高效的特点,若运用得当,往往能化繁为简、化难为易.下面仅以此法的运用为例,谈谈微专题的设计与实施,以抛砖引玉.
教学目标 (1)通过计算同一图形(三角形、特殊四边形等)的面积,体会“积不离高,高不离积”的思维策略和构建方程解决问题的特点; (2)经历面积法解决问题的过程,并通过不同方法的对比,体验解决问题的不同思路,感受面积法的精巧之处;(3)能结合所学知识,灵活运用面积法解决较为复杂的问题,体会其中的数学思想(如数形结合、转化思想、方程思想).
教学重点 引导学生通过自主探索和方法对比,感受面积法的简洁、高效的特点.
教学难点 如何结合所学知识,根据题目的特点,灵活运用面积法构建方程解决问题.
2 教学过程
2.1 创设情境,引导探究
随着上课铃声响起,教师微笑着走进教室,但没有说话,而是在黑板上写下四个字“今日说法”.(学生充满期待,多数人充满疑惑,这是讲法律还是数学?)
师:同学们,今天我们不讲法律,只谈方法,一种简洁而又高效的解题方法,请看问题1.
2.2 方法对比,体会等积

图1
问题1如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BC=3,AC=4,你能求出CD的长吗?
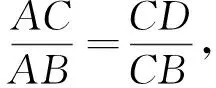
生2:我用的是勾股定理,设AD=x,则BD=5-x,分别在Rt△ACD和Rt△CBD中计算CD2,列出方程求解.
生3:我是分别在Rt△ACD和Rt△ABC中表示出sinA,构造等式求解.
师:还有补充的吗?
生4:计算△ABC的面积也可以求出CD的长.
师(追问):请具体一点!
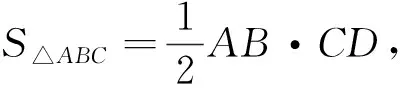
师(高兴地):很好!这种方法我们称之为“面积法”(教者接着“今日说法”下面补上板书“——面积法”),这种方法有什么特点?
生5:将三角形的面积计算了两次.
师:对!其关键是抓住同一个三角形,从两个不同的角度计算其面积,列出方程求解.请大家接着看下面的问题.

图2
问题2如图2,若将问题1中的高CD去掉,改为点D是Rt△ABC斜边AB上的一个动点,过点D作DM⊥AC,DN⊥BC,垂足分别为M,N,则MN的最小值是多少?
(不少学生陷入困境,无法对MN进行有效的转化)

师(追问):在解决问题的过程中你能体会到怎样的思想方法?
生6:转化.
师:很好!这里有一幅“对联”送给大家(教师展开准备好的对联分别挂在黑板两侧):“积不离高,高不离积”,它生动诠释了面积法的特点,我们怎样理解这幅对联的含义呢?
生7:“积不离高”是指计算某图形的面积通常离不开高;“高不离积”是指有了高(垂直)就要注意向计算某图形面积的方向去思考.
师:说得太好了!那谁来给这幅对联添加一个横批?
生8(脱口而出):面积法.
(老师展开横批“面积法”,贴在黑板上方的正中央)
教学说明对于问题1,学生有多种方法可供选择,但最简洁明了的还是面积法,在引出面积法后又为解决问题2做好了铺垫.在问题2中,利用“矩形对角线相等”的性质先把MN转化为CD,将陌生的问题熟悉化,再结合问题1中的结论来求解.设置问题1的意图有两个,一是以此作为“种子题”,让学生掌握一种解决问题的方法,为下面进行面积法的运用做好铺垫,二是结合本题让学生从中体会“积不离高、高不离积”的策略,通过方法对比,帮助学生积累解题经验,体会解题的策略,训练思维的多样性和灵活性.
2.3 变换载体,方法迁移
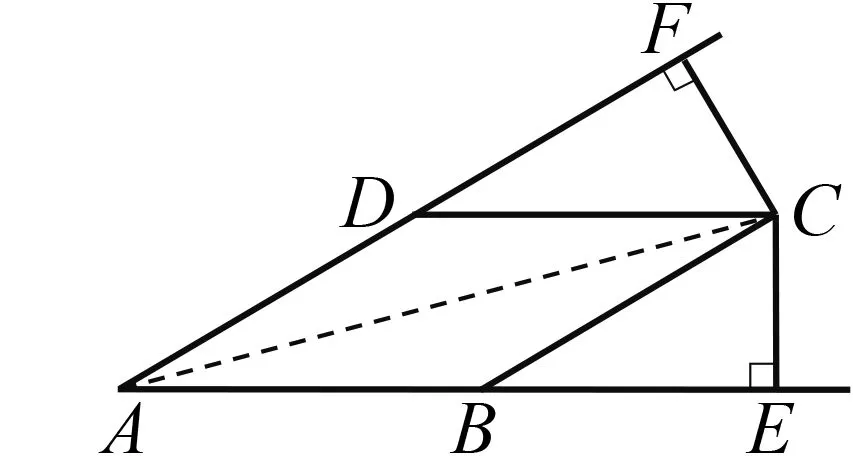
图3
问题3如图3,已知四边形ABCD是菱形,CE⊥AB,CF⊥AD,垂足分别为E,F,求证:CE=CF.
生9:由菱形的性质可知CB=CD,∠CBA=∠CDA,可以考虑证明△CBE≌△CDF(AAS),从而证得CE=CF.
师:很清晰的思路!还有不同想法吗?
生10:连结AC,由菱形ABCD可知AC平分∠DAB.因为CE⊥AB,CF⊥AD,所以CE=CF.
师(追问):为什么?
生10:角平分线上的点到角两边的距离相等.
师:很好!能熟练运用菱形的性质.若类比问题1的解题思路,还有没有其他想法?
生11(恍然大悟):计算菱形的面积.
师(追问):具体一点,怎么算?
生11:因为S菱形=AB·CE=AD·CF,由菱形ABCD可知AB=AD,所以CE=CF.
(教室里响起了欢呼声和掌声……)
教学说明遇到此类证明线段相等的问题,不少学生首先想到的方法是证明三角形全等,也有少数学生会选择运用角平分线定理来证明,但很少有学生想到计算菱形ABCD的面积,建立方程解决问题.教学过程中,教者先让学生各抒己见,在思维碰撞中体会运用面积法解题的简洁性.虽然本题难度不大,但由于大家对解法进行了比较,放大了题目本身的价值,体现了面积法的精髓——“积不离高,高不离积”,拓宽了学生的思维空间,促进了学生数学素养的提升.
2.4 构建模型,隐藏“题”中
问题4如图4,在等腰三角形HBC中,HB=HC,E为底边BC上的任意一点,EF⊥HB于点F,EG⊥HC于点G,BM⊥HC于点M,试探究EF,EG,BM之间的数量关系.
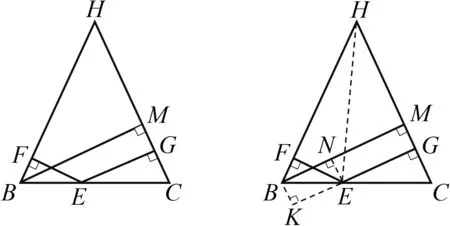
图4 图5
生12:如图5,过点E作EN⊥BM,垂足为N,则四边形EGMN为矩形,所以EG=NM,再证得△BEF≌△EBN,故有EF=BN,所以EF+EG=BM.
师:很好!这种方法是将最长的线段截为两段,我们称之为“截长”法,还有不同方法吗?
生13:还有“补短”法,如图5,过点B作BK⊥GE,交GE的延长线于点K,用同样的思路可以证得矩形BKGM和△BEF≌△BEK,从而得到结论.
师:完全正确,两种方法合起来可称之为“截长补短”法.如果我们再换个角度看问题,由EF⊥HB我们还能想到什么?
生14:可以计算△HBE的面积.
师(追问):结合EG⊥HC,BM⊥HC,我们又能想到什么?
生14:计算△HCE,△HBC的面积.
师(再追问):那接着怎么运用这些三角形的面积呢?
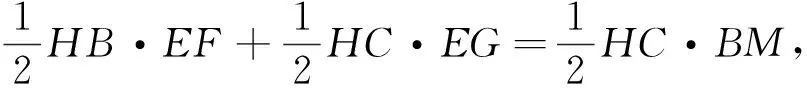
师(追问):当等腰三角形HBC的顶角为直角或钝角时,结论还成立吗?
(小组分工合作完成……)
生16(小组代表):成立,方法一样,还是运用面积法.
师:请大家归纳出一个一般性的结论.
生17:等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高.
师:很好!下面,我们就来看看这个结论在解题中的运用.
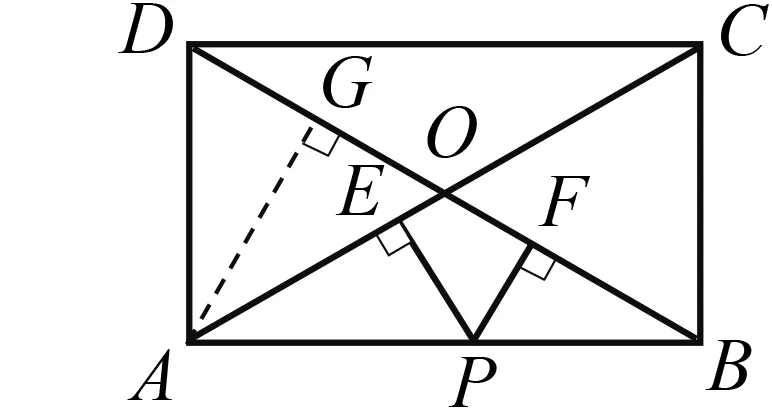
图6
问题5如图6,已知矩形ABCD中,AB=4,BC=3,P为AB边上任意一点,且PE⊥AC,PF⊥BD,E,F分别为垂足,求PE+PF的值.
生18:先根据条件证明△OAB是等腰三角形,则PE+PF的值等于该等腰三角形一腰上的高.
师(追问):然后呢?
生18:过点A作AG⊥BD,垂足为G,则PE+PF=AG.
师(再追问):那如何求AG呢?
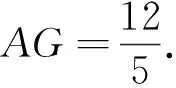
教学说明教学过程中,教者可视学情予以适当引导,当学生想不出面积法时,教者可以引导学生从三条高入手,以面积为抓手,建立方程解决问题.问题4的“慢加工”为问题5的“快处理”铺平了道路.通过问题变式和不断追问,让学生逐步明晰运用面积法解题的特点和规律,抓住面积法的本质,实现解题经验的正向迁移和解题方法的有效应用,引领学生的思维向着问题深处漫溯.
2.5 巧借k值,妙用等积
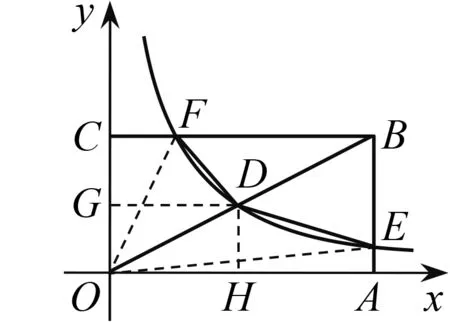
图7

(问题出示后,学生遇到困难、陷入沉思……)
师:连结OE,OF,四边形OEBF的面积与四边形BFDE的面积有何关系?
生20:因为点D为OB的中点,所以S△OBF=2S△DBF,S△OBE=2S△DBE,所以S四边形OEBF=2S四边形BFDE=9.
(先独立思考,后分组讨论)
生21:过点D作DH⊥OA,DG⊥OC,垂足分别为H,G,S矩形OABC=4S矩形OHDG=4k.
师(追问):为什么?
生21:因为点D是OB的中点,即点D是矩形OABC的对称中点.
师(再追问):然后呢?

师:太好了!列出这个方程用到“积不离高,高不离积”吗?
生(疑惑地):没有?
师:所以没有高的情况下,我们也可以运用“割补法”将某个图形的面积“算两次”,然后列出方程求解!
教学说明学生遇到困难时,通过教者的引导、追问,让学生在深入思考的过程中体会反比例函数中k的几何意义,再借助于矩形OABC的 面积不变巧妙地建立方程求解.微专题这种教学形式为学生进行有效联想和方法建构提供了便利和可能,通过系列化的活动和体验,把对知识、 方法和规律的掌握过程演变成学生能力提升的过程.
2.6 归纳小结,一“法”多得
师:回顾本节课所解决的问题,我们会发现始终有一根主线贯穿“题”中,这是一种什么方法?
生(齐):面积法.
师(追问):你是怎样理解这种方法的?
生22:把同一个图形的面积用不同的方法算两次,但“有时无高胜有高!”(不一定有高),建立等量关系,运用方程解决问题.
……
教学说明通过追问,让学生重新审视面积法,加深对这种方法的理解,完善方法体系,构建“多题一法”,形成分析问题和解决问题的能力,达到因“微”而专、见微知著的效果.
3 回顾与反思
3.1 教学设计的立意
“授人以鱼不如授人以渔”,其意思实质上是指传授给人既有知识,不如传授给人学习知识的方法.道理其实很简单,鱼是做事目的,捕鱼是做事的手段,一条鱼能解一时之饥,却不能解长久之饥,如果想永远有鱼吃,那就要真正学会捕鱼的方法.在本节微专题课中,专门从解题的方法——面积法展开探究,将“授人以渔”的理念诠释得通彻透亮.因此,掌握一种方法就犹如拥有一样得心应手的工具,拥有解决问题的“本领”,这是学生长远发展的必由之路.“种树者必先培其根,学习者必先培其法.”只有授人以渔,才能从根本上得其法.以“微专题”的方式将解决问题的方法进行归类、提炼与运用,更高效地让学生学会解决问题,使更多的学生拥有捕鱼的本领,变输血为造血,才是我们的终极目标.
3.2 教学反思
(1)坚持结合学情,按需设计
微专题开发与实施应当立足学情,基于教情,按需开发,不必拘泥于固定的形式和内容,可以灵活设计并实施.例题可以根据学情按需选用.“今日说法——面积法”就是在学生知识结构基本完成的基础上,将偶尔运用的面积法归类处理,由“分散运用”为“集中梳理”,实现系统化、脉络化.同时,微专题教学的有效性要通过教学实践加以检验,坚持从实践中来,到实践中去,遵循“开发—设计—实践—修正”到“再实践—再修正……”的实施路径,注重校正优化以及再实施再优化的过程,实现深度学习下的螺旋式上升.微专题设计必须根据学生的学习现状进行,使之更适合学生的学情,做到“适合的才是最好的!”微专题的实施必须尊重不同学生,做到量身定做、一次一课,增强教学的针对性和有效性.
(2)坚持以生为本,因材施教
微专题设计和实施过程中要坚持面向全体学生,突出以生为本,让学生喜闻乐见、兴趣盎然,把握好“低起点”“多层次”“富挑战”的要求,体现基础性、层次性和综合性的特点.以学生对此方法的理解和运用为目标,实现思维深处的拓展提升,面积法的教学设计就体现了这样的特点.首先“今日说法”这个标题足够吸引学生,今日说法究竟要说什么“法”?激发学生的好奇心和求知欲,也为学生学好用好此法埋下伏笔.其次,对涉及面积法的题目遵循由易到难、由浅入深的编排,问题设置富有启发性、应用性、延续性,引例必须是一颗充满生命力的种子,只有这样,后续问题才能生根发芽.所以微专题教学必须始终坚持以学定教、因材施教,学为中心、以教促学,教者要花更多的精力从学生的视角来看待问题,精心设计课堂问题和探究活动,引导学生积极思考、主动探究,在优化思维的过程中解决问题,促进学生的个性发展和能力的提升.
(3)坚持以小见大,微中见法
微专题的开口小,容量大,有深度,重方法,学习者学过之后往往体会深刻,回味无穷!微专题设计方式灵活多样,可以对某个知识板块进行专题复习,也可以对某些数学模型进行变式探究,还可以就某种数学方法进行专项指导,亦或是某种数学思想的深度感悟等.设计内容和上课形式不拘一格,灵活机动,针对性强.教学实施注重相机而教,因情而生,灵动生成.本课例中的面积法属于“多题一法”的专题研究,通过不同载体的变换,将计算面积这一方法从直角三角形过渡到菱形、矩形,通过两次计算同一载体的面积列出方程解决问题,实现了形与数的有机统一.对同一题目不同方法的横向对比与不同题目同一方法的纵向梳理,拓宽了学生思维的空间,凸显了面积法的简洁、高效的特点,达到了以小见大、微中见法的目的.

