基于不同物理参数化方案的中小流域降雨径流集合预报

田济扬，刘荣华，刘含影，丁留谦

(1.中国水利水电科学研究院，北京100038；2.水利部防洪抗旱减灾工程技术研究中心，北京100038)

气象水文耦合洪水预报方法逐渐受到防汛部门的关注，其最大的优势是可延长洪水预报的预见期，为防汛决策争取到宝贵时间，特别是对于汇流时间短的中小流域而言意义重大[1]。近年来，随着计算机计算效率的提升，数值大气模式预报的气象要素分辨率显著提高，能够实现精细化降雨预报，使气象水文耦合下的中小流域洪水预报成为可能[2-3]。

尽管数值降雨预报有了长足的进步，但局地降雨预报存在很大的不确定性，定量、定时、定点预报还有很大的提升空间，能否在中小流域的洪水预报中得到应用还需进一步研究[4]。集合预报是降低预报不确定性的有效方法。目前数值降雨预报集合成员的组成方式主要有3种[5-7]：一是对初始场进行随机扰动，为数值大气模式提供有差异的初值条件，形成集合预报集，多用于已知天气形势下的数值大气模式模拟效果测试；二是采用不同的数值大气模式对同一场降雨进行预报，不同的数值大气模式构成集合预报集，多用于中国气象局、欧洲中长期天气预报中心等的业务预报；三是基于不同的物理参数化方案组合，构建集合预报集，多用于未知天气形势下的降雨预报。物理参数化方案用于表征小于模式网格分辨率的湍流运动以及发生在分子尺度的物理过程，不同的物理参数化方案对降雨产生的次网格过程的描述重点不同，而物理参数化方案的选取对模式的模拟或预报结果影响较大[8-9]。单一物理参数化方案难以适应不同的降雨过程，给预报带来很大的不确定性，基于物理参数化方案的集合预报能较好地解决降雨预报不确定性的问题，从而为流域洪水预报提供较为可靠的降雨信息[10]。

选取福建省梅溪流域为研究区，将WRF(weather research and forecasting)模式与梅溪流域分布式水文模型耦合，基于WRF模式设置了36种物理参数化方案组合进行降雨预报，并将其作为梅溪流域分布式水文模型的输入开展集合洪水预报研究。此外还讨论了直接采用GFS(global forecasting system)降雨数据和WRF模式数值预报后处理的降雨数据分别作为分布式水文模型的输入进行洪水预报的效果。

1 研究区及资料

1.1 研究区概况

梅溪为闽江的一级支流，主要位于闽清县境内，流域面积956 km2，土地利用以林地和耕地为主，土壤类型以黏壤土和砂黏壤土为主(图1)，在我国东南沿海地区具有较强的代表性，能够反映该地区中小流域的降雨产流特性。梅溪流域多年平均降雨量1 560 mm，受台风及地形影响，强降雨发生频次较高，平均每2～3 a就会发生一次洪灾，给下游人口聚集的闽清城关造成严重威胁。在梅溪流域开展降雨洪水预报研究，将有助于提升流域暴雨洪水的预警预报能力，保障下游防洪安全，不仅具有一定的理论价值，还具有重要的现实意义和显著的社会经济效益。

图1 梅溪流域土地利用及土壤类型

1.2 数据与资料

来源于NCEP(National Centers for Environmental Prediction)的GFS数据用于驱动数值大气模式开展数值降雨预报，其分辨率为1.0°×1.0°，预报时长可达192 h。梅溪流域内共有8个雨量站和1个水文站，1989—2016年雨量站和水文站的长系列观测资料用于分布式水文模型的率定与验证，以及降雨与洪水预报精度的评价。流域的地形地貌资料主要来源于国家地理信息中心，包括1∶5万DEM、30 m和优于(含)2.5 m分辨率的数字正射影像数据(DOM)[11]，其中土地利用和植被类型数据是基于DOM提取解译并通过调研核查得到的。土壤类型来自全国第二次土壤普查数据，结合《中国土种志》生成土壤质地数据。

大量研究[12-13]表明，数值大气模式更容易准确预报时空分布较均匀且降雨量级适中的降雨，对短时强降雨的预报效果较差。为此，选取降雨时空分布较为均匀的典型场次——2012年“苏拉”台风引发的流域降雨过程(场次Ⅰ)，以及流域常见的时空分布极不均匀的典型场次——2014年“海贝思”台风引发流域降雨过程(场次Ⅱ)，开展降雨径流集合预报研究。场次Ⅰ降雨历时24 h(2012年8月3日00:00-2012年8月3日24:00)，累积降雨量为84 mm，洪峰流量992 m3/s；场次II降雨历时24 h(2014年6月17日21:00-2014年6月18日21:00)，累积降雨量为66 mm，洪峰流量1 170 m3/s:见图2。

图2 场次Ⅰ(苏拉台风引发)和Ⅱ(海贝思台风引发)的降雨洪水过程

2 气象水文耦合系统

2.1 WRF模式与设置

作为新一代中尺度数值大气模式，WRF模式不断对物理参数化方案进行补充，并修改完善动力框架，使其能够较成功地再现或预报中尺度天气过程，适用于中尺度不同天气形势下高精度的降雨模拟与预报[14-15]。降雨预报结果选用相对误差ER评价累积降雨量，临界成功率ICS和均方根误差ERMS评价降雨时空分布的预报结果[16-17]。ER和ERMS值越低、ICS值越高，降雨预报效果越好。用于定性评价的临界成功率指标ICS由分类变量NA、NB、NC求得，详见参考文献[18]。

2.1.1WRF模式基本设置

为了在降低计算成本的前提下提高模式降雨预报的水平分辨率，研究依托WRF模式的动力降尺度方法，设置了3层嵌套网格，通过逐级增加区域水平分辨率的方式提高数值预报的分辨率，在WRF模式中采用分析松弛(analysis nudging)对模式区域空间场的每一个格点进行调整，达到对降尺度后边界条件修正的目的[19-20]。相邻嵌套层的嵌套比例为1∶3，网格尺寸由内至外分别为4、12、36 km[21-22]。最内层网格完全覆盖研究区，最外层网格基本覆盖了影响研究区天气形势的大地形、海洋和主要天气系统，使中小尺度天气过程引起的有效变化都包括在该层网格的覆盖范围内，降雨预报结果选用分辨率最高的内层网格(4 km×4 km)，WRF模式的基本设置见表2。

表2 WRF模式基本参数设置

2.1.2物理参数化方案集合

考虑到微物理过程、积云对流方案、长短波辐射对降雨模拟结果的影响较大[23-24]，设置了36种不同的物理参数化方案组合(表3)。边界层选用典型的非局地边界层方案Yonsei University(YSU)，陆面方案选用运行较稳定的Noah[25]。

表3 物理参数化方案集合

2.2 梅溪流域分布式水文模型

中国山洪水文模型CNFF-HM为梅溪流域分布式水文模型的构建提供了技术框架[26]。梅溪流域分布式水文模型由蒸散发模型、产流模型、汇流模型、河道演进模型等组成，其中蒸散发模型选用3层蒸散发模式，产流模型为三水源蓄满产流模型，汇流模型采用标准化单位线，河道演进模型为动态分段马斯京根法。按照汇水关系将梅溪流域划分为60个子流域，见图3。其中，最大的子流域面积为31.6 km2，最小的子流域面积为1.45 km2，平均流域面积为15.7 km2，与数值大气模式预报的4 km×4 km分辨率吻合。模型洪水模拟与预报结果评估选用洪峰流量误差Rf、峰现时间误差Δt、纳什效率系数ENS[27-28]。

图3 子流域划分结果

采用SCE-UA算法[29]，选取梅溪流域1989—2016年56场降雨径流资料对梅溪流域分布式水文模型的参数进行率定与验证。其中,1989—2003年发生的38 场降雨洪水过程用于模型参数的率定，2004—2015年发生的18场降雨洪水过程用于模型参数的验证，18场洪水模拟的洪峰流量误差Rf均值为9.52%，峰现时间误差Δt均值为1.17 h，ENS均值为0.83。经过率定后的分布式水文模型在梅溪流域的适应性较强。其中，不同场次土壤初始湿度值根据场次定义开始时间前10天降雨量经蒸发折减得到。率定后模型参数取值见表4，模型率定结果见表5。

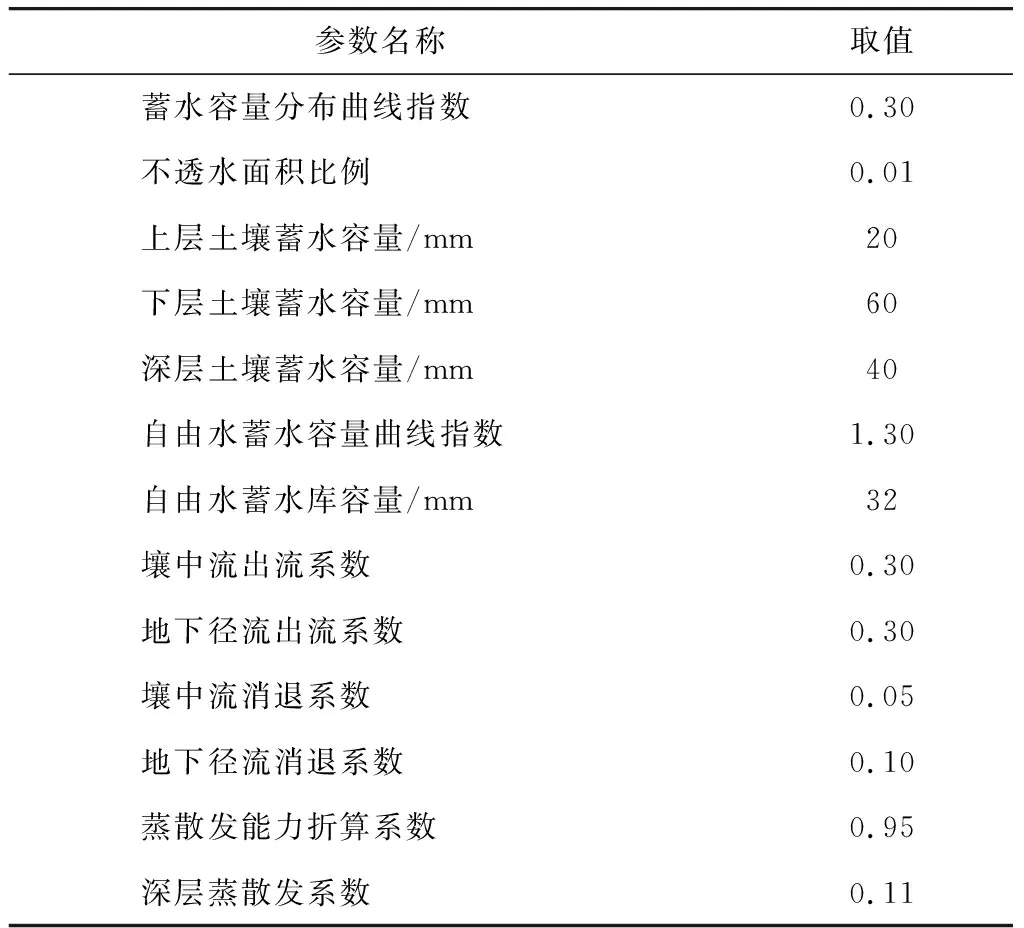
表4 梅溪流域分布式模型参数取值

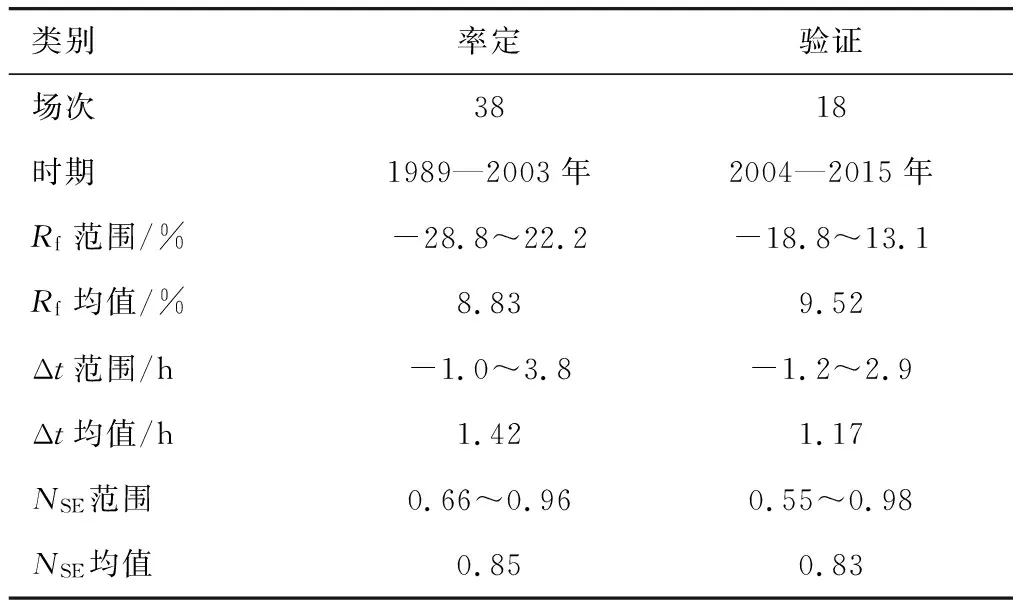
表5 模型率定与验证情况

Rf=(Q′f-Qf)/Qf

(1)

Δt=T′-T

(2)

(3)

式中：Q′f和Qf分别为场次洪水洪峰流量的模拟值与实测值，m3/s；T′和T分别为模拟与实测的峰现时间，h；Q′i和Qi分别为洪水过程中第i小时的模拟值与实测值，m3/s。

2.3 耦合系统

气象水文耦合系统由WRF模式和梅溪流域分布式水文模型耦合而成。耦合系统的驱动数据为GFS，GFS逐6 h更新1次(00:00、06:00、12:00、18:00)，即耦合系统逐6 h预报1次未来192 h的降雨过程，降雨预报结果每6 h更新1次，WRF模式输出的预报降雨为4 km×4 km分辨率的逐小时降雨量值；逐小时降雨量作为梅溪流域分布式水文模型的输入，进行洪水预报。因此，耦合系统最关键的是实现网格降雨与子流域单元降雨的转化[30-31]。网格降雨转化为子流域单元降雨遵循两个原则：一是子流域全部落在预报降雨的网格内时，子流域面雨量与网格降雨量一致；二是子流域不完全在一个预报降雨的网格内时，子流域面雨量由与子流域有重叠部分的各网格预报降雨加权平均求得，其中权重系数为子流域与各预报降雨网格重叠部分占子流域面积的比例[32-33]。集合预报时，36个物理参数化方案组合同时进行降雨预报，形成36种降雨预报结果，再采用36种预报降雨结果驱动梅溪流域分布式水文模型进行洪水预报。耦合系统的预报过程见图4。

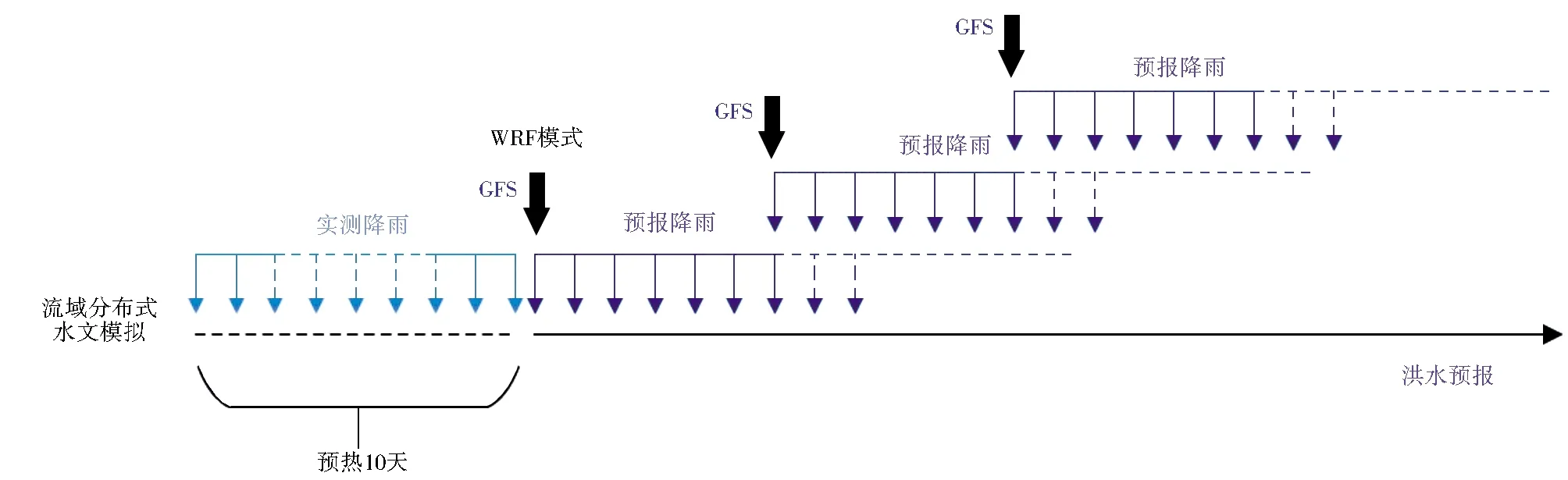
图4 耦合系统预报过程

3 计算结果

3.1 降雨预报结果

基于36种试验方案，计算出两场降雨的24 h面累积降雨量预报值与实测值的相对误差ER、空间与时间2个维度的临界成功率ICS、空间与时间2个维度的均方根误差ERMS，结果见表6。36个方案的降雨模拟空间分布见图5。场次Ⅱ计算结果见表7。36个方案的降雨模拟空间分布见图6。

图5 36个方案下场次I降雨预报的空间分布

图6 36个方案下场次Ⅱ降雨预报的空间分布

由表6可知，36个方案的相对误差ER值为0.88%～21.00%，ER最小的是方案13，最大的是方案25。对于降雨空间分布的评估：36个方案的临界成功率ICS值为0.736 8～0.758 2，各方案间的差异较小，ICS最大的是方案29；36个方案的均方根误差ERMS值为0.133 1～0.221 6，RMSE最小的是方案24，最大的是方案5。对于降雨时程分布的评估：36个方案的ICS值均为0.687 5；36个方案的ERMS值为0.592 4～0.760 0，ERMS最小的是方案17，最大的是方案30。总体来看，WRF模式对该场降雨的预报效果较好，基本能够重现该场降雨的量级及时空分布特征，但不同物理参数化方案下的数值降雨预报结果各有优缺点，采用降雨集合预报的方式开展气象水文耦合洪水预报更为合理。

表6 36个方案下场次I降雨预报结果及排名

由表7可知，36个方案的相对误差ER值为24.32%～68.51%，ER最小的是方案13，最大的是方案19。对于降雨空间分布的评估:36个方案的ICS值为0.347 0～0.487 9，ICS最小的是方案1，ICS最大的是方案13；36个方案的ERMS值为0.521 6～0.845 1，ERMS最小的是方案12，最大的是方案19。对于降雨时程分布的评估:36个方案的ICS值为0.329 2～0.435 6，ICS值最小的是方案1，最大的是方案36；36个方案的ERMS值为1.300 1～1.634 9，ERMS最小的是方案13，最大的是方案2。每个方案的降雨模拟结果均有较明显的差异，这表明不同物理参数化方案下的降雨模拟与预报存在很大的不确定性。WRF模式对“海贝思”台风在梅溪流域引起的降雨模拟效果较“苏拉”台风引发的降雨场次差。两场降雨的量级相近，但“苏拉”台风引发的降雨时空分布相对均匀，而“海贝思”台风引发的降雨属于短历时局地强降雨，WRF模式对该类型降雨的捕捉效果较差。

表7 36个方案下场次Ⅱ降雨预报结果及排名

3.2 气象水文耦合洪水预报结果

对于场次Ⅰ，得到的36个降雨预报方案下的洪水预报结果见图7。不同方案下预报的洪峰流量误差Rf为4.21%～24.60%，Rf最小的是方案15，最大的是方案21。不同方案下预报的峰现时间误差Δt为-5～0 h，Δt最小的是方案22，而方案1、2、3、4、7较大；36个方案的纳什效率系数ENS为-0.977 9～-0.005 0，ENS最小的是方案16，最大的是方案21。以洪峰流量误差Rf、峰现时间误差Δt、纳什效率系数ENS这3项指标来评估洪水预报结果，较难在36个方案中选出最优的洪水预报结果。

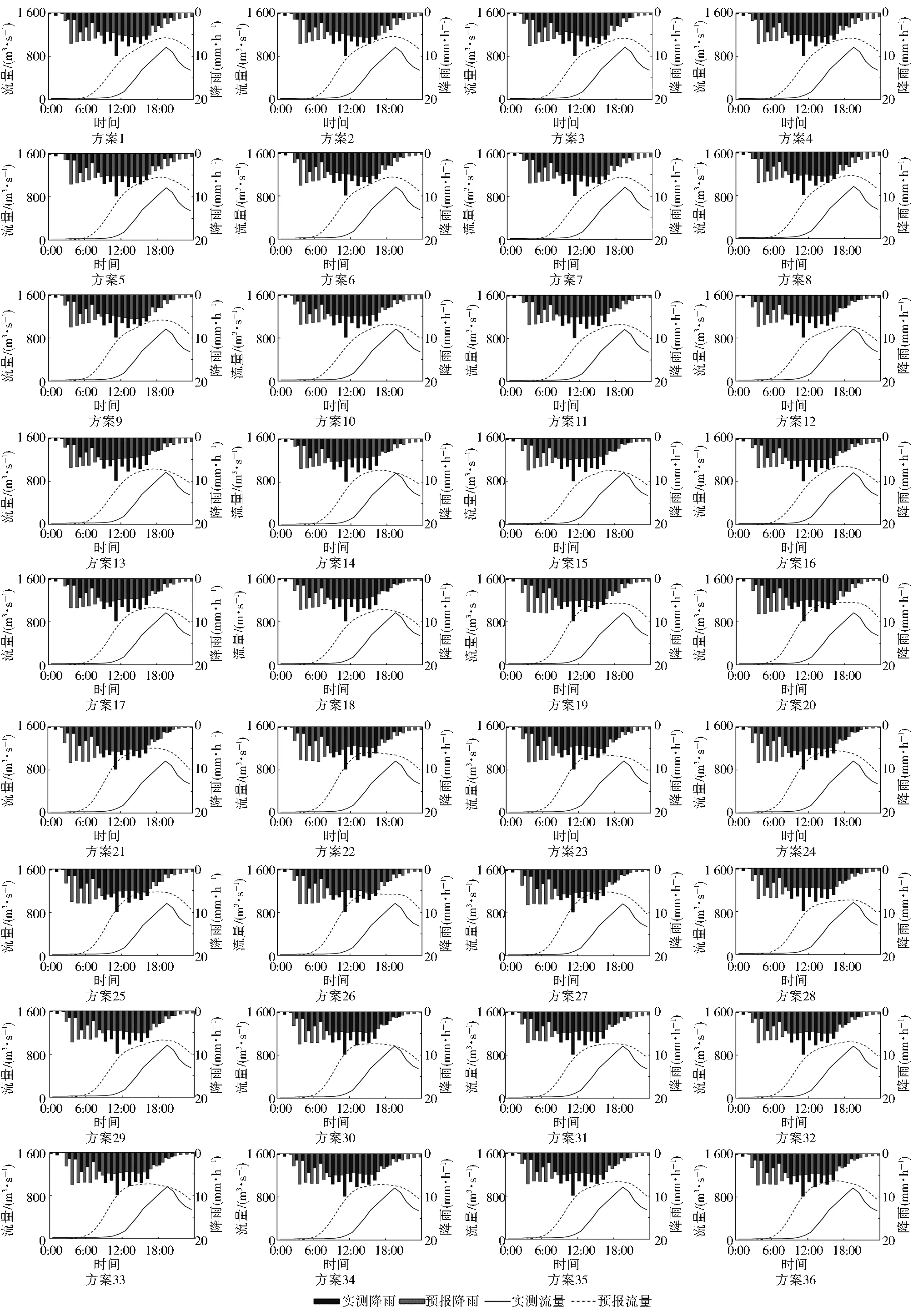
图7 36个方案下场次Ⅰ的降雨洪水预报结果

对于场次Ⅱ，36个降雨预报方案下的洪水预报结果见图8。不同方案下预报的洪峰流量误差Rf为-95.1%～-79.0%，Rf最小的是方案15，最大的是方案5。不同方案下预报的峰现时间误差Δt为0～1 h，Δt为0的方案有方案5、6、10、11、12，Δt为0的方案有方案1、2、3、4；36个方案的纳什效率系数ENS值为-0.341 8～-0.185 7，ENS最小的是方案4，最大的是方案15。以洪峰流量误差Rf、峰现时间误差Δt、纳什效率系数ENS这3项指标来评估洪水预报结果，同样难以在36个方案中选出最优的洪水预报结果。

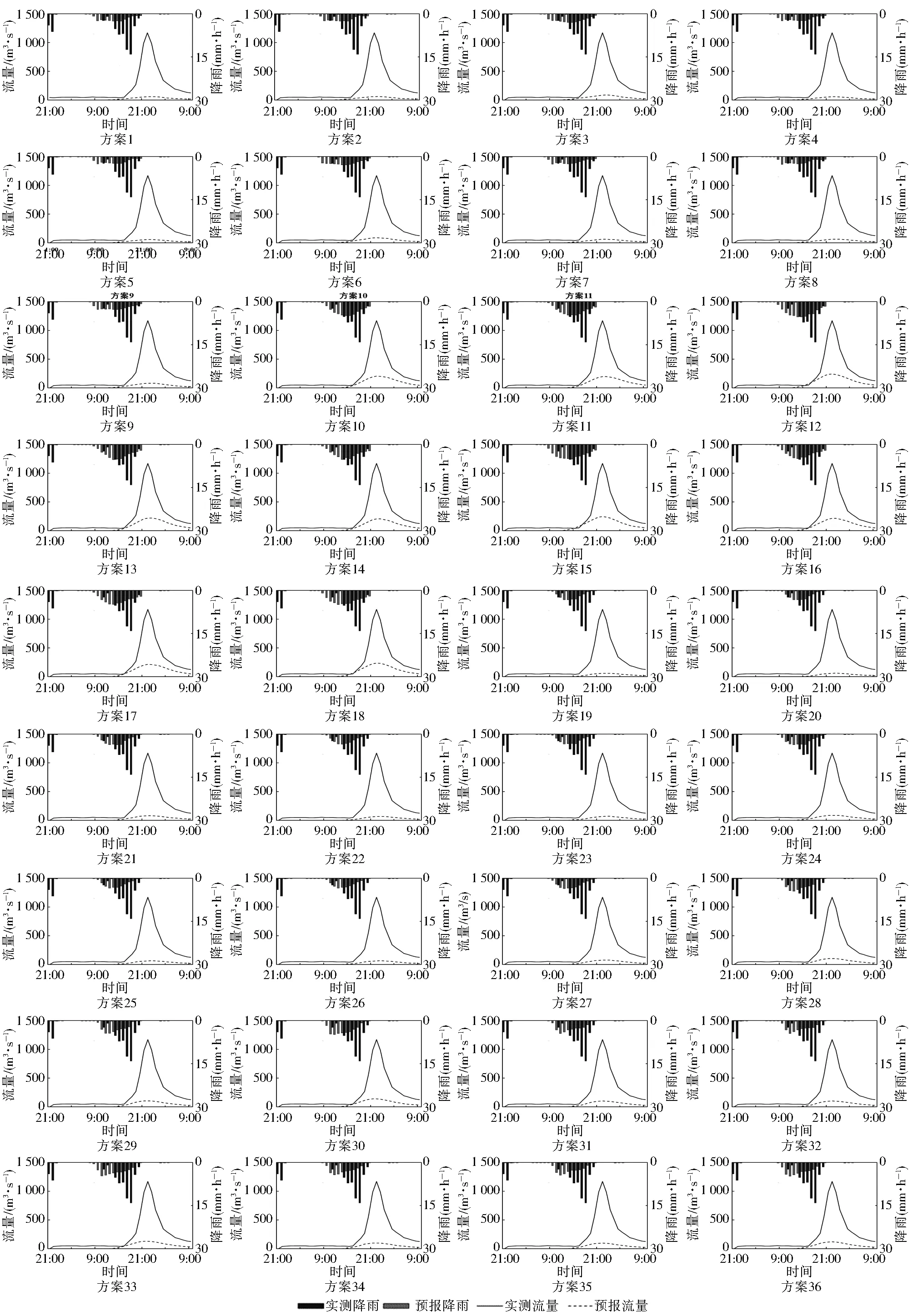
图8 36个方案下场次Ⅱ的降雨洪水预报结果

受初始场和侧边界条件等影响，数值大气模式很难准确描述大气运动的真实状态。对于某一场降雨而言，在其产生前很难判定哪一种物理参数化方案适合应用于该场降雨，为数值降雨预报带来很大的不确定性。将36个预报方案作为一个集合，选择每个预报方案下同一时刻洪水预报结果的中位数作为最终预报结果。集合中值预报相比单一预报方案更加稳定可靠。由图9可知，集合预报结果相比较单一方案的预报不确定性降低，避免选择的单一预报方案导致最差的预报结果，可信度更高。且对于“苏拉”台风引发的时空分布较均匀的降雨，相应洪峰流量预报误差为Rf为11.30%，峰现时间误差Δt为-2 h，总体预报结果较好；而“海贝思”台风引发的短历时强降雨，相应洪峰流量预报误差为Rf为-86.89%，峰现时间误差Δt为-1 h，预报结果较差，主要原因是相对中小流域尺度的降雨预报要求，模式驱动数据的分辨率较低，提供的初始场和侧边界条件不够精确，导致模式的误差随运行时间的延长而不断积累放大，对于“海贝思”台风引发的短历时强降雨(降雨集中在4 h内)而言，6 h更新1次的驱动数据无法准确跟踪描述变化迅速的天气形势。

图9 场次Ⅰ和Ⅱ洪水集合预报结果

总体来看，由于WRF模式在降雨空间维度上预报效果较好，而时间维度上预报效果略差，特别是预报降雨早于实测降雨，导致预报洪水起涨较快。中小流域以防洪减灾为目的的洪水预报更关注洪峰流量和峰现时间。本研究开展的气象水文耦合预报预见期≥6 h，对于时空分布较为均匀的降雨场次，气象水文耦合预报能够准确反映对应洪水过程的洪峰量级，相比采取“落地雨”进行洪水预报具有一定优势；对于时空分布不均匀的降雨场次，受数值降雨预报精度影响，气象水文耦合预报未能较准确反映对应洪水过程的洪峰量级，依然有很大改进空间。

4 讨论与分析

4.1 GFS数据直接驱动下的洪水预报

有研究[34]表明，提高数值降雨预报的分辨率不一定有助于提高洪水预报精度。为此，采用分辨率较粗的GFS数据直接作为梅溪流域分布式水文模型的输入开展洪水预报，并与上述基于WRF模式开展的集合预报结果进行对比。GFS数据直接驱动下的洪水预报结果见图10，场次Ⅰ和Ⅱ预报的洪峰流量误差Rf分别为24.59%、-94.54%，峰现时间误差Δt分别为-2 h、1 h，纳什效率系数ENS值分别为-0.265 2、-0.304 7，预报效果较集合预报差，其主要原因是对于不到1 000 km2面积的梅溪流域，1.0°×1.0°的分辨率太粗，无法反映降雨的空间分布特征。

图10 GFS数据驱动下的洪水预报与集合预报结果对比

4.2 降雨预报后处理下的洪水预报

由于场次Ⅱ的集合预报误差依然较大,为提高洪水预报精度，降雨预报数据往往需要进行后处理。采用基于异方差扩展型Logistic算法而发展的统计后处理模型对WRF模式集合预报结果进行后处理[35]。处理后的降雨预报数据再作为梅溪流域分布式水文模型的输入进行洪水预报。结果表明，场次Ⅰ和Ⅱ预报的洪峰流量误差Rf分别为3.97%、-48.59%，峰现时间误差Δt分别为0、0.5 h，纳什效率系数ENS值分别为0.520 0、0.677 3，较处理前有了明显提升，结果见图11。

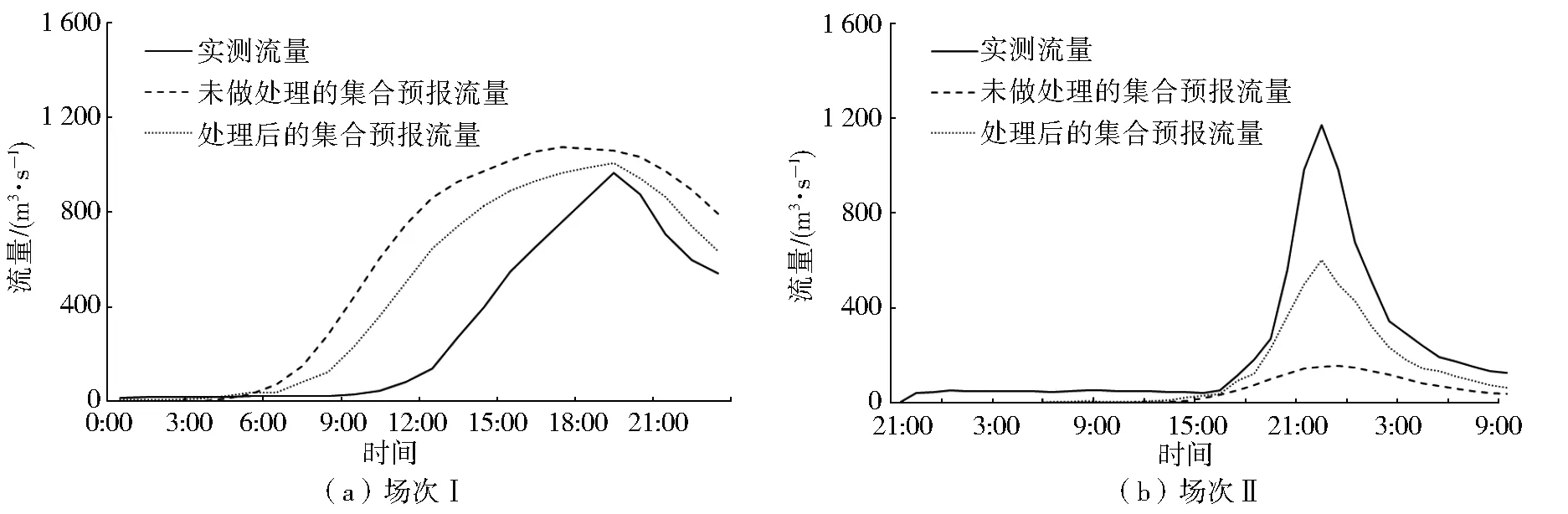
图11 降雨预报数据处理前后场次Ⅰ和Ⅱ洪水预报结果

5 结 论

本研究选取东南沿海地区的梅溪流域为研究区，在建立36种物理参数化方案的基础上形成了降雨径流集合预报集，构建了基于WRF模式和梅溪流域分布式水文模型的气象水文耦合模型，开展降雨径流集合预报。以2012年“苏拉”台风和2014年“海贝思”台风引发的梅溪流域降雨洪水事件为例，分析了气象水文耦合模型的降雨径流集合预报效果，得到以下主要结论:

在不同物理参数化方案下，降雨空间分布比降雨时间分布的预报效果更好，对于“苏拉”台风引发的降雨过程，36个方案下的ER为0.88%～21.00%，空间维度ICS为0.736 8～0.758 2、ERMS为0.133 1～0.221 6，时间维度ICS均为0.687 5，ERMS为0.592 4～0.760 0，对于“海贝思”台风引发的降雨过程，36个方案的ER值为24.32%～68.51%，空间维度ICS为0.347 0～0.487 9、ERMS为0.521 6～0.845 1，时间维度ICS为0.329 2～0.435 6、ERMS为1.300 1～1.634 9。

采用降雨集合预报的方式开展气象水文耦合洪水预报更为合理，能够有效降低洪水预报的不确定性，选择每个预报方案下同一时刻洪水预报结果的中位数作为最终预报结果，对于“苏拉”台风引发降雨洪水事件，洪峰流量误差为Rf为11.30%，峰现时间提前2 h，对于“海贝思”台风引发的降雨洪水事件，洪峰流量误差Rf为-86.89%，峰现时间误差Δt为-1 h。

经过降雨预报数据的后处理，对于“苏拉”台风引发降雨洪水事件，洪峰流量误差Rf为3.97%，峰现时间误差Δt为0，对于“海贝思”台风引发的降雨洪水事件，洪峰流量误差Rf为-48.95%，峰现时间误差Δt为0.5 h，因此数值降雨预报宜在处理后用于流域洪水预报。

基于WRF模式和梅溪流域分布式水文模型的气象水文耦合洪水预报预见期≥6 h，对于时空分布较为均匀的降雨场次，气象水文耦合预报能够准确反映对应洪水过程的洪峰量级，相比采取“落地雨”进行洪水预报具有明显优势；对于时空分布不均匀的降雨场次，受数值降雨预报精度影响，气象水文耦合预报还有一定提升空间。

集合预报可有效降低降雨预报的不确定性，但并不能从根本上提高降雨预报精度。气象水文耦合洪水预报主要受降雨预报精度影响，进一步研究可在耦合系统中加入数据同化算法改进降雨预报效果，提高短历时强降雨情境下的洪水预报准确性。