月径流随机模拟序列优选方法

刘欣欣，马细霞,2，程旭，王倩丽，张静文

(1.郑州大学水利科学与工程学院，郑州 450001;2.郑州大学黄河生态保护与区域协调发展研究院，郑州 450001)

径流序列作为水资源系统的输入项，通常用来分析系统未来的发展趋势。通过水文随机模型生成足够长的径流序列，可以弥补实测资料代表性不足的缺陷，已广泛应用于水库(群)优化调度[1-2]、水资源系统风险分析[3-4]等领域。

目前，水文随机模型的精度评价常采用“统计一致性”准则，即生成的模拟序列必须和实测资料具有相近的统计特征。如:Weiss等[5]以均值、均方差、滞后1和滞后2的自相关系数作为检验指标，对实测序列和模拟长序列的高分位数进行比较，评估季节性自回归模型[SAR(p)]保持实测序列统计特征方面的性能。Hao等[6]以科罗拉多河为研究对象，通过分析月径流模拟序列基本统计参数的相对误差，发现平均值、标准差和偏度的相对误差均小于10%，滞后1的自相关系数相对误差均小于20%，由此得出了模拟序列能较好地保持实测序列截口统计特征的结论。Hamid等[7]采用平均绝对百分比误差(EMAP)等方法来分析模拟结果的均值、标准差、偏态系数和最大值，根据EMAP的最小值表示最佳模式，优选出最适合的季节性自回归综合移动平均模型。高瑞忠等[8]采用平均相对误差和平均绝对误差方法，评价巴拉格尔河流域年季尺度下的径流量模拟效果，据此得出了神经网络方法对该流域径流量进行模拟总体适用性较好的结论。传统评价方法在保证模拟系列均值、方差等基本统计特征较为一致的情况下，能够模拟出具有不同时空分配特性的径流过程，对水库(群)优化调度、水资源系统风险分析、水资源工程规模确定具有重要意义。

径流过程是十分复杂的随机过程，但也具有一定的统计规律，譬如年内分配过程具有汛期和非汛期的交替变化特征，同一地区汛期最大4个月所处月份基本固定，多年平均最大4个月水量占全年平均水量的比例也较为稳定。径流模拟序列具有不同的时空分配特性，若仅保证模拟系列均值、方差等基本统计特征较为一致，则有可能存在某些年份的年内分配过程不合理问题，因此基于此模拟序列获得的应用成果存在一定的安全风险。为此，马细霞等[9]引入样本熵指标对径流序列的复杂特性进行检验，结果表明样本熵指标能大体诊断出模拟序列内较大月径流量和位置的异常情况，但其合理性没有得到充分论证。

以往评价方法的不足之处在于未能全面检验模拟序列年内复杂变化的特性，因此，有必要增加一些反映径流时序变化的特征指标，如连续最大4个月径流百分率[10]、径流年内分配不均匀系数、径流年内集中度[10-11]等，在保证模拟序列年内分配多样性的同时，排除年内分配异常的情况。此外，同一随机模型所生成的模拟序列在时程变化上差异较大[9]，以往的评价方法在工程规划设计和风险分析方面，未能筛选出最适宜的径流模拟序列。鉴于此，本文提出截口-复杂性指标体系，以淮河流域河南段干支流上的典型水文研究站月径流随机模拟为应用实例，对季节性自回归模型模拟序列的截口特性和复杂特性进行全面检验，并基于灰色关联分析法对以往指标体系和截口-复杂性指标体系的计算结果进行优选和分析，以期为月径流随机模型模拟序列优选提供理论依据。

1 模拟序列评价指标体系及指标量化

1.1 评价指标体系构建

为全面评价模拟序列，本文从以下2个方面构建截口-复杂性指标体系。截口特征方面：均值、变差系数、偏差系数反映序列截口统计特性，相邻截口滞时1、2的自相关系数反映径流序列的时间相依特性。这些指标在随机模拟序列检验中已得到广泛利用，故本文仍将其作为月径流随机模拟效果评价的主要指标。复杂特性方面：河川径流的时空分布规律是水资源评价的重要内容，也是河流类型和水利规划的一项重要指标[12]，本文引入连续最大4个月径流百分率、集中度和不均匀系数作为反映径流变化过程的指标，以期更好地反映实测序列与模拟序列年内分配的复杂特征。样本熵表示非线性动力学系统产生新信息的概率，主要用来定量地刻画系统的规则度及复杂度[13]，当用于度量时间序列复杂性时，其值越大，序列产生新信息的概率越高，序列越复杂[14]。由于其较少地依赖于时间序列长度，所需数据序列短、计算成果更为稳定，已在水文气象研究领域广泛应用，因此可以作为描述径流序列复杂性特征的指标[15]。传统评价指标与截口-复杂性指标体系对比见表1。

1.2 评价指标量化方法

截口参数采用统计学方法计算[16]，以下主要介绍样本熵、集中度和不均匀系数的计算方法。

1.2.1样本熵计算

设原始数据为X(1),X(2),…,X(N)，共N点，可按如下步骤计算其样本熵[17]。

按序号连续顺序，组成一组m维矢量，从Xm(1)到Xm(N-m+1)，其中

Xm(i)=[x(i),x(i+1),…,x(i+m-1)],i=1～N-m+1

(1)

定义X(i)与X(j)之间的距离d[Xm(i),Xm(j)]为两者对应元素中差值最大的一个，即

d[Xm(i),Xm(i)]=max(|x(i+k)-x(j+k)|)，

k=0～m-1;i,j-1～N-m+1;i≠j

(2)

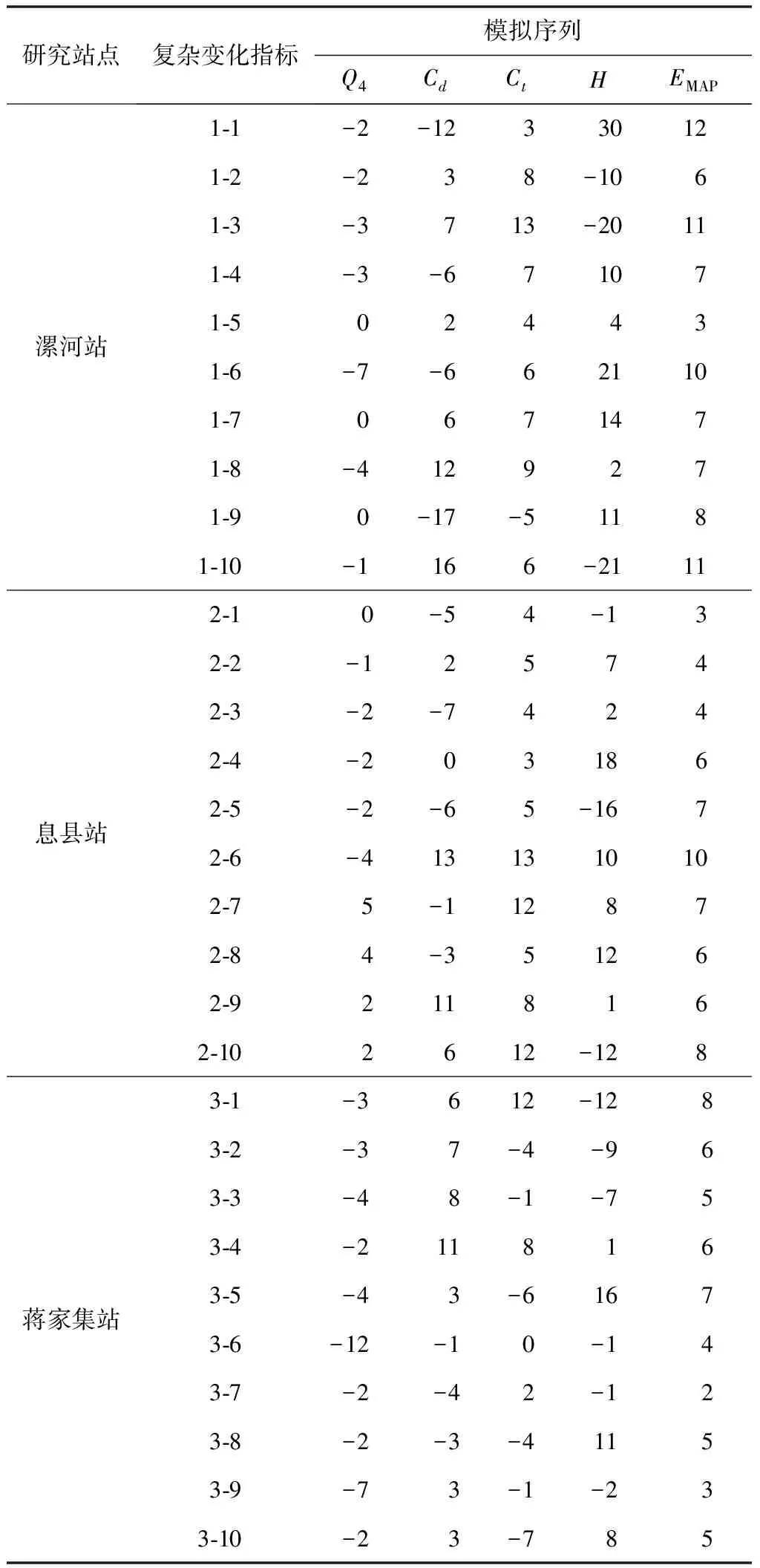
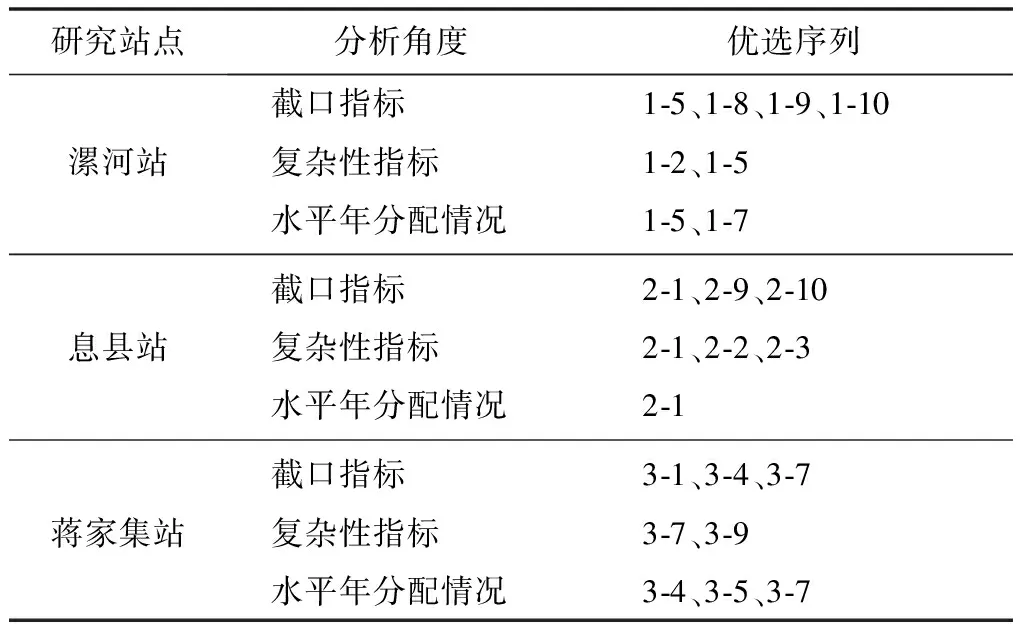
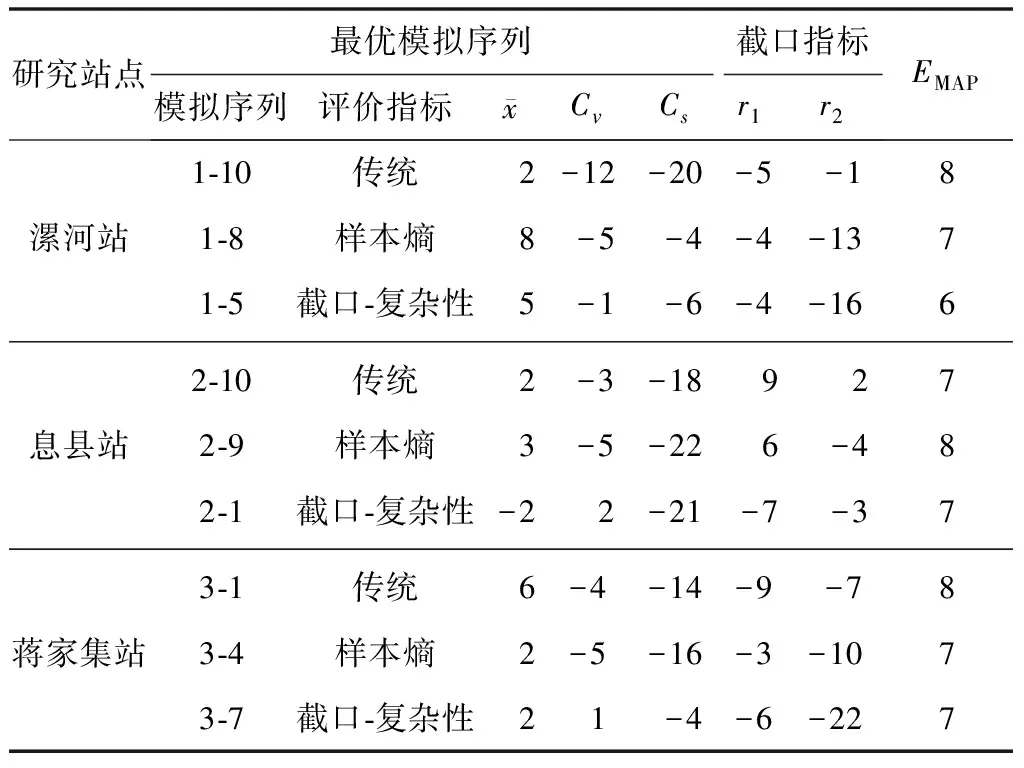
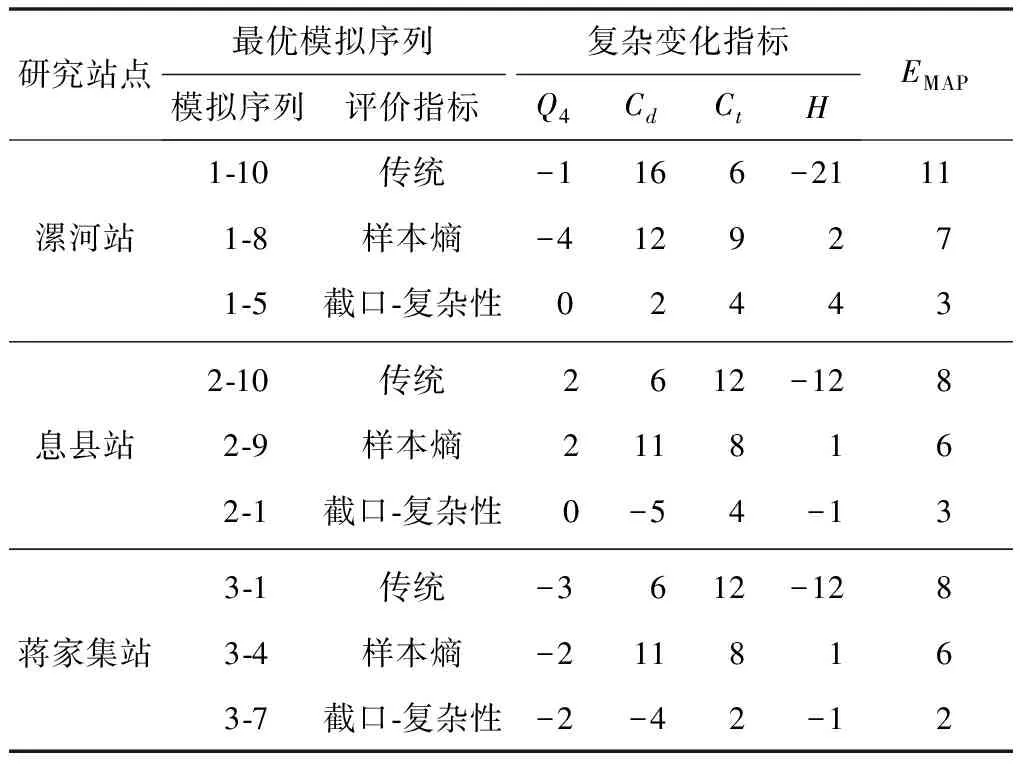
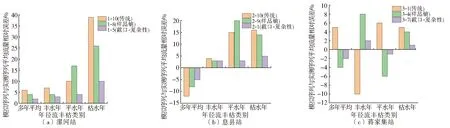
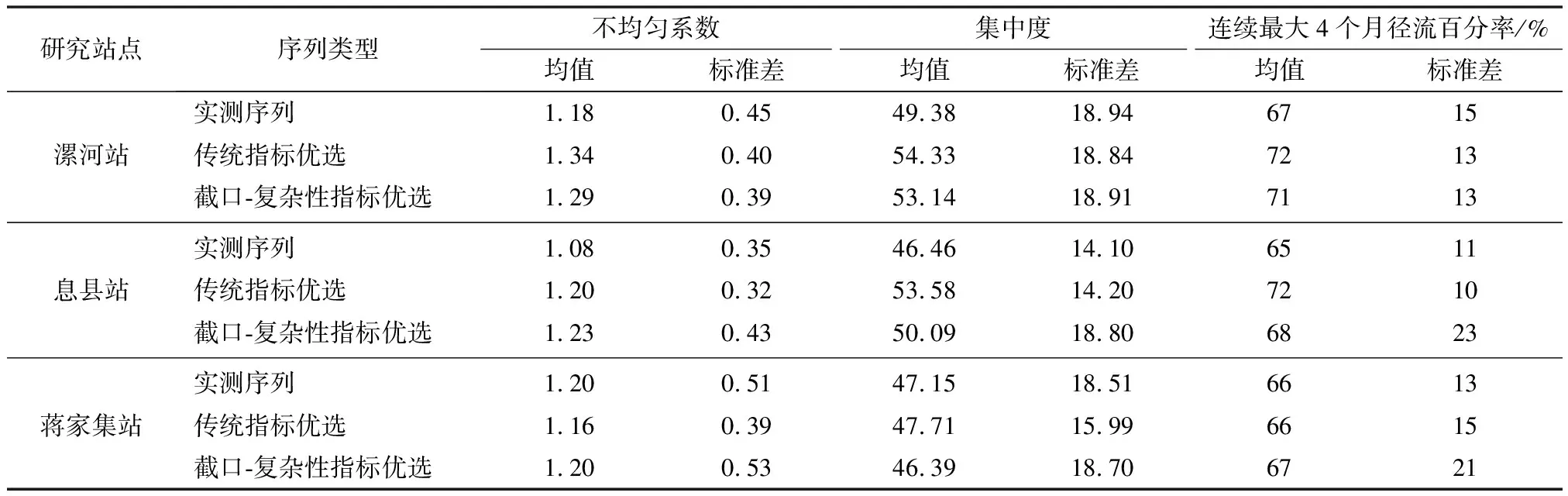
给定阈值r，对每一个1≤i≤N-m值，统计d[Xm(i),Xm(j)]

Bm,i(r)={d[Xm(i),Xm(j)]

(3)

求其对所有i的平均值，即

(4)

将维数增加1，变为m+1维矢量，重复式(1)～(3)的步骤后，得

(5)

式中：Bm(r)和Bm+1(r)分别为m点和m+1点两序列相似的概率，则序列理论上的样本熵

(6)

当N为有限时，得出序列样本熵估计值

H(m,r,N)=-ln[Bm+1(r)/Bm(r)]

(7)

参数m、r的选择是样本熵估计的关键，但目前尚无最佳标准，通常m=2，r=0.2SD(SD为原始序列的标准差)[17]。

1.2.2集中度计算

径流在年内的集中程度用集中度(Cd)表示，计算公式[18]为

(8)

式中：R为多年平均月径流计算得出的年径流量；Rx、Ry分别为12个月份 (i=1,2,…,12)的分量之和所构成的水平、垂直分量，其中

(9)

式中：ri为第i月平均月径流；θi为第i月份对应的方位角，以各月月中值代表的角度数值来表示。

1.2.3不均匀系数计算

不均匀系数(Ct)的计算公式[19]为

(10)

式中：Ct(t)为第t年的径流年内分配不均匀系数；σ(t)为第t年的年内时段平均流量的均方差；Q(t)为第t年的平均流量，m3/s；λ为月份，λ=1,2,…,m，此处m=12。径流年内分配不均匀系数反映了对径流调控的难易程度。对于n年系列的不均匀系数的均方差，其值越大，则表示径流不均匀性的年际变化越大。

1.3 评价指标分析方法

平均绝对百分比误差(EMAP)属于无量纲统计量，可以在不同变量间进行比较，其值越小，说明模型模拟或预测的精确度越高，因此可表征各评价指标中模拟序列的精度。EMAP的计算公式为

(11)

式中：Ai为实测序列第i个指标计算值；Fi为模拟序列第i个指标计算值。

2 随机模拟序列的灰色系统评价方法

随机模拟生成径流序列最基本的假定是未来事件应具有和实测序列相同的随机性质，这就要求生成的模拟序列必须和实测资料具有相近的统计特征，这也是优选随机模型和评价生成序列的主要依据。灰色关联分析法是一种衡量因素的发展态势和特征变化相似程度的方法，通过灰色关联度表征数据序列之间联系的紧密程度。本文采用灰色关联分析法，计算模拟序列与实测资料在截口、复杂性指标的综合关联度，优选较为理想的随机模拟序列。灰色系统关联分析的具体步骤如下[20]。

确定参考数列与比较数列。本文采用截口-复杂性指标体系中的9个指标作为月径流序列的特征指标，由实测序列统计所得的9个特征指标值构成参考数列X0，第i个随机模拟序列统计所得的9个特征指标值构成比较数列Xi(i=1,2,…,n)。

X0={x0(1),x0(2),…,x0(9)}

(12)

Xi={xi(1),xi(2),…,xi(9)}

(13)

式中：x0(1),x0(2),…,x0(9)分别为参考数列X0的9个特征指标值；xi(1),xi(2),…,xi(9)分别为比较数列Xi的9个特征指标值。

指标值的无量纲化处理。计算公式为

(14)

(15)

式中：x0(k)为参考数列X0的第k个特征指标值；xi(k)为比较数列Xi的第k个特征指标值；yi(k)为比较数列Xi第k个特征指标的效果测度；k=1,2,…,9。

求参考数列与比较数列的灰色关联系数。计算公式为

ξi(k)=

(16)

式中：ξi(k)为参考数列X0与比较数列Xi第k个特征指标的关联系数；ρ为分辨系数，表示平均分辨水平，其值为0～1，一般取0.5[20]。

求参考数列与比较数列的加权关联度。为便于从整体上比较模拟序列，有必要将各指标的关联系数集中为一个值，即加权关联度为ri，其表达式为

(17)

式中：ωi(k)为比较数列Xi第k个特征指标的权重，考虑到截口特性、复杂变化特性方面的各指标重要性相当，故本文采用等权处理，即：ωi(k)=1/9。加权关联度越大，说明相应的模拟序列在各指标的综合评价中表现越好。

3 实例分析与讨论

3.1 研究区概况及数据来源

淮河是河南省内流域面积最大的水系，境内控制流域面积8.83万km2，占淮河流域总面积的32%，占河南省总面积的53%。为验证本文方法的合理性和有效性，在淮河干流、沙河和史河支流上，分别选取流域面积相差较大的息县(10 190 km2)、漯河(12 150 km2)和蒋家集水文研究站(5 930 km2)月径流随机模拟为应用实例，以期为淮河流域中上游径流模拟序列选取提供理论支撑。以上3站实测年月径流资料(1951—2018，共68年)均来源于《河南省水情手册》，这些资料均通过了“三性”审查，可以用于模拟计算。

3.2 季节性自回归模型建立

根据RIC定阶方法[21]，计算漯河站、息县站、蒋家集站SAR(p)模型不同月份的RIC值。其中：漯河站和息县站12个月的RIC最小值对应阶数均为1阶；蒋家集站除11月份外，其余11个月RIC最小值对应的阶数均为1阶。因此，根据RIC 准则，3个水文站均采用SAR(1)模型进行随机模拟。

3.3 随机模拟序列精度分析

通过所建SAR(1)模型，随机生成10组样本容量为680年的模拟序列，样本的选取具有随机性。为便于分析，将漯河站10组模拟序列记为1-1、1-2……1-10，息县站记为2-1、2-2……2-10，蒋家集站记为3-1、3-2……3-10。采用相对误差和平均绝对百分比误差(EMAP)，从截口、复杂变化方面分析模拟序列的拟合效果，并结合模拟序列多年平均及各水平年年内分配情况，验证截口、复杂变化特性指标评价的合理性。

3.3.1截口统计特性精度分析

模拟序列截口指标的相对误差和EMAP结果见表2。由表2可知，各水文站10组模拟序列在截口特性方面的精度存在差异，3个水文研究站的10组模拟序列的均值和变差系数相对误差均在15%范围内，偏态系数的误差相对较大，一阶自相关系数的误差平均值在8%以内，二阶自相关系数的误差平均值在15%范围内。EMAP计算结果表明:漯河站EMAP值最小的是1-5序列，其次是1-8、1-10、1-9序列；息县站EMAP值最小的是2-1、2-10序列，其次是2-9序列；蒋家集站EMAP值最小的是3-4、3-7序列，其次是3-1序列。与同一水文研究站的其他模拟序列相比，这些模拟序列在截口统计特性评价中表现较好。

表2 模拟序列截口指标相对误差及EMAP结果统计Tab.2 Statistics of RE and EMAP results of simulated sequence section index %

3.3.2复杂变化特性精度分析

模拟序列复杂变化指标的相对误差和EMAP结果见表3。可以看出，同一水文研究站各模拟序列在复杂变化特性方面的精度存在差异。其中：3个水文站连续最大4个月径流百分率、不均匀系数的相对误差在13%范围内；集中度、样本熵指标变化幅度较大，说明模拟序列在集中程度和复杂特性方面差异较大。EMAP计算结果表明：漯河站EMAP值最小的是1-5序列，其次是1-2序列；息县站EMAP值最小的是2-1序列，2-2、2-3序列次之；蒋家集站EMAP值最小的是3-7序列，其次是3-9序列。与同一水文研究站的其他模拟序列相比，这些模拟序列较好保持了实测序列在形态变化方面的特性。

表3 模拟序列复杂变化指标相对误差及EMAP统计Tab.3 Statistics of RE and EMAP results of complex change index of simulation sequence %

3.3.3模拟序列精度综合分析

为验证截口-复杂性指标体系的合理性，采用距平百分率法对径流序列进行丰、平、枯划分，统计各站模拟序列多年平均及丰、平、枯水年年内分配的相对误差，结果见图1。可以发现：漯河站模拟序列丰、平水年以及多年平均月径流的拟合效果相对较好，相对误差均在20%范围内，枯水年各序列间相对误差差异较大，年内分配总体拟合较好的是1-5、1-7序列；息县站模拟序列各水平年及多年平均的相对误差在25%范围内，丰水年的相对误差均在12%范围内，年内分配总体拟合较好的是2-1序列；蒋家集站模拟序列多年平均及各水平年的相对误差整体在25%范围内，各序列相对误差差异明显，年内分配总体拟合较好的是3-4、3-5、3-7序列。

图1 各站模拟序列多年平均以及丰/平/枯水年相对误差Fig.1 The relative errors of the simulated series of each station in annual average,wet,normal and dry years

对比模拟序列截口、复杂性精度分析结果与水平年精度分析结果 (见表4)，可以看出：同一水文研究站的模拟序列在截口、复杂变化特性方面拟合效果相差各异。例如：漯河站模拟序列1-8、1-9、1-10在截口统计特性评价中EMAP值较小，说明其较好的保持了实测序列截口统计特性，但在复杂变化特性和年内分配过程方面EMAP值均较大；蒋家集站3-7、3-9序列复杂变化指标的EMAP值相差较小，分别为2%和3%，截口指标的EMAP值分别为7%和14%，上述序列在复杂变化特性方面拟合效果相差较小，但保持实测序列截口统计特性的效果相差较大。单独使用截口或复杂性指标进行评价，不能保证模拟序列年内分配方面的拟合效果。例如息县站的2-2、2-10序列，分别在复杂性、截口指标中EMAP值较小，但其平、枯水年及多年平均情况下的相对误差均较大。综合上述分析，需要全面考虑模拟序列截口、复杂变化特性方面的拟合效果。

表4 模拟序列不同角度精度分析结果对比Tab.4 Comparison of accuracy analysis results of different angles of simulation sequence

3.4 模拟序列优选

基于截口-复杂性指标体系，采用灰关联分析法对模拟序列进行优选，结果见表5。由表5可以看出漯河站、息县站和蒋家集站最优模拟序列分别为1-5序列、2-1和3-7序列。

表5 模拟序列的关联度Tab.5 Correlation degrees of simulated sequences

为进一步说明截口-复杂性指标体系用于模拟序列评价的合理性，对传统指标、样本熵最小指标[9]以及截口-复杂性指标体系优选出的模拟序列进行对比，截口、复杂变化特性方面的相对误差和EMAP见表6和表7，多年平均以及丰、平、枯水年的拟合效果见图2。

表6 3种评价指标优选序列截口指标的相对误差及EMAP结果统计Tab.6 Statistics of RE and EMAP results of optimized sequence section indexes of three evaluation indexes %

表7 3种评价指标优选序列复杂性指标的相对误差及EMAP结果统计Tab.7 Statistics of RE and EMAP results of complex change index of three evaluation index optimization series %

由表6和表7可以看出：3种指标优选的模拟序列截口指标的EMAP值差异较小，最大为2%；复杂变化指标的EMAP值差异较大，截口-复杂性指标体系和传统指标优选序列的EMAP值最大相差8%，与样本熵指标优选序列的EMAP值最大相差4%。由图2可以看出，截口-复杂性指标体系优选序列的各水平年年内分配相对误差总体小于传统指标和样本熵指标优选序列的结果，且平、枯水年相对误差差异最为明显。

图2 3种评价指标优选序列多年平均及丰/平/枯水年相对误差Fig.2 The relative errors of three evaluation index optimization series in annual average,wet,normal and dry years

综合上述分析，3种指标评价方法优选序列的精度为：截口-复杂性指标>样本熵指标>传统指标。这说明本文提出的截口-复杂性指标体系是切实可行的，有利于全面评价径流模拟序列，实现不同随机模拟序列之间的比较与优选。

3.5 讨 论

截口、复杂性及水平年内分配方面的对比结果表明，3种指标优选的序列均较好地保持了实测序列的截口特性，但传统指标、样本熵最小指标体系不能全面评价模拟序列，有可能遗漏径流序列重要的细节信息。以下从年内分配异常情况和时程分配(过程)的差异性两方面进行探讨。

根据3个水文站历年逐月实测径流资料统计结果，漯河站、息县站、蒋家集站多年平均汛期最大4个月(6—9月)径流量占全年径流量分别为67%、64%、61%。现将连续最大4个月径流出现在非汛期视为异常情况，统计传统截口指标优选序列、截口-复杂性指标体系优选序列年内连续最大4个月径流在非汛期的百分率，并与实测资料进行对比(表8)，结果发现：传统指标优选序列的百分率在3种序列类型中最大，且与截口-复杂性指标优选序列的情况相差较大。这说明只保证模拟系列均值、方差等基本统计特征较为一致情况下，模拟序列会出现较多的年内分配异常情况，而截口-复杂性指标体系有助于排除年内分配异常的情况。

表8 3种径流序列连续最大4个月径流在非汛期的百分率Tab.8 Percentage of the maximum 4-month continuous runoff of three runoff series in non-flood season

表9统计了漯河站3种序列的年内分配指标，可以看出：截口-复杂性指标体系优选序列的标准差数值整体大于传统指标优选序列，说明本文指标体系增加的复杂变化指标并没有影响模拟序列各子序列年内分配特征的多样性；两种指标优选序列与实测序列的标准差差异较小，说明传统指标体系和截口-复杂性指标体系优选的长序列模拟序列中，各子序列的多样性受多年平均计算条件下各指标约束的影响较小。

表9 3种径流序列年内分配指标分析Tab.9 Analysis of annual distribution index of three runoff series

模拟序列截口、复杂变化特性的评价以及年内分配异常情况的检验表明，引入表征复杂变化特性的指标(Q4、Cd、Ct、H)，可以在保证模拟序列多样性的同时，减少年内分配的异常情况，能够描述传统评价指标所忽略的细节特征，较好地体现原始序列的形态复杂变化特征。因此，截口-复杂性指标体系更准确、真实地刻画了月径流模拟序列的年内复杂变化特征，优选出的模拟序列更能保持实测序列的时间变化特征。

4 结 论

本文从径流序列非线性及复杂特性出发，提出了月径流随机模拟序列评价指标体系，并将其用于3个水文站季节性自回归模型的模拟序列效果评价中，得到以下结论。

只考虑截口统计参数的评价方法，忽视了径流序列的复杂变化特性，可能遗漏重要的细节信息，从而影响模拟序列检验的精度。截口-复杂性指标体系中表征复杂变化特性的指标(Q4、Cd、Ct、H)能简单有效地区分模拟序列保持实测资料复杂变化特性的能力，优选序列在年内分配方面的EMAP值最小，总体拟合效果最好。

对传统指标、样本熵最小指标以及截口-复杂性指标优选的序列进行了分析，结果表明截口-复杂性指标体系优选的序列能较好地反映实测序列的变化过程和复杂特性，综合截口和复杂变化特征方面的分析，月径流随机模拟序列优选方法的优劣顺序为截口-复杂性指标>样本熵指标>传统指标。

经过截口和复杂变化特征方面的模拟序列评价、年内分配异常情况分析以及时程分配(过程)差异性分析的多重验证，截口-复杂性指标体系在保证模拟序列年内分配多样性的同时可以减少年内分配异常的情况，有助于水文工作者掌握不同模拟序列之间的差异，更加全面地评价径流模拟序列，从而提供更加准确的水文模拟序列。

为进一步提高径流序列模拟效果评价的准确性，未来将考虑采用主成分分析法找出相互独立的主要影响指标，以此构成更具代表性的指标体系，并由此对随机模拟序列进行检验，通过与其他指标体系检验结果的对比分析其代表性。