基于MP-PIC方法的冶金硅氢氯化流化床反应器模拟

吴诗鸣，陈皓宁，宗原，许志美，赵玲

（华东理工大学化学工程联合国家重点实验室，上海 200237）

引 言

多晶硅是目前光伏能源以及芯片制造行业中不可或缺的原材料[1-3]。在目前的主流工艺中，如西门子法[4]，通常会副产大量的四氯化硅（STC）[5-6]。冶金硅氢氯化反应通过将四氯化硅与冶金硅以及氢气反应可以实现四氯化硅的循环利用[7]。其总反应方程式为

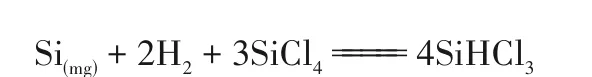
反应为可逆弱放热反应[8]。工艺中反应温度通常在500～600℃之间。根据Mui[9]的研究，反应由以下两步可逆反应串联构成。

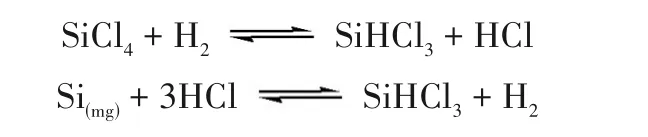
其中第一步反应是气相均相反应，反应速率较慢，是整个反应过程的速率控制步骤。第二步反应是气固非均相反应，反应速率较快。丁伟杰[10]的研究表明第一步反应在600℃以下受到动力学限制，冶金硅表面的杂质对气相反应具有催化作用。因此，在工艺温度下，氢氯化反应主要发生在冶金硅颗粒表面。Sill[11]的研究表明催化剂对于冶金硅氢氯化反应的进行至关重要。相比冶金硅颗粒表面的杂质铁元素，添加金属铜催化剂可以明显加快反应。Becker[12]认为金属铜对反应的催化过程与冶金硅颗粒表面固有的铁元素催化过程是并行的，并提出了相应的动力学模型。

冶金硅氢氯化反应通常在流化床反应器中进行。流化床反应器具有良好的传热传质特性，同时操作压降小，可以实现反应过程的连续化操作[13]。然而，流化床反应器内复杂的流动与反应过程使得反应器放大较为困难。Colomb 等[14]采用两相模型[15]对冶金硅氢氯化实验流化床反应器进行模拟，计算结果与Sill 等[11,16]的实验结果吻合较好。由于两相模型中对气泡相以及乳化相的运动进行了简化处理，其中的流动模型不能真实反映反应器中的流场。因此，由反应器放大引起的流场变化需在模型中进行修正[17]。

相比经典的两相模型，计算流体力学（CFD）方法可以模拟反应器内流场以及组分分布情况，已经成为指导反应器放大与优化的重要方法[18]。Liu等[19]采用双流体模型与群体平衡方法耦合计算的方式对硅烷热裂解流化床反应器进行模拟，探究了影响硅颗粒生长的内在机制以及操作条件对生长速率的影响。此外，基于该模型又进一步探究了动力学模型对于模拟结果的影响[20]。Li 等[21]采用双流体模型对生产多晶硅颗粒的内循环流化床反应器进行了模拟，探究了操作气速对流化床在传热性能以及抑制壁面沉积等方面的影响，并给出了气速的最优操作范围。 本文结合MP-PIC（multiphaseparticle in cell）方法对小试冶金硅氢氯化反应器进行数值模拟。MP-PIC 方法是一种面向工业级流化床模拟的计算方法。该方法最早由Andrews 等[22]提出，由Snider 等[23-25]发展成熟并开发出商业化软件。MP-PIC 模型中对流体相采用欧拉方法描述；对于颗粒相采用计算颗粒（parcel）代替真实颗粒群，同时采用经验的应力模型简化颗粒间的相互作用，从而大幅减小了计算量[26]。

本文在Sill 等[11,16]的实验基础上对实验级流化床反应器进行模拟。根据反应动力学模型的特点，在网格以及计算颗粒包含的真实颗粒数量无关性的基础上探究了反应器内初始三氯氢硅（TCS）浓度对模拟结果的影响。基于模拟与实验验证结果，进—步对反应器内的反应与流动进行了分析。对不同压力以及进口H2∕STC 摩尔比操作条件下的TCS产率进行了研究。研究结果可以为反应器的放大与优化提供参考。

1 数值方法

1.1 MP-PIC模型

1.1.1 气相方程 气相质量守恒方程为

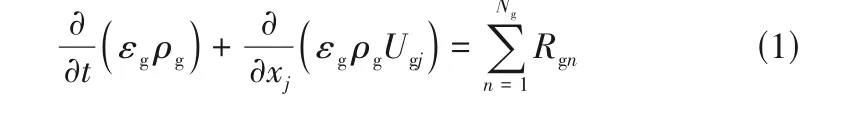
式中，εg为气相体积分数；ρg为气体密度；Ugj为气体速度在j方向的分量；Ng为气体组分数；Rgn为气体组分n的消耗或者生成速率。

气相动量守恒方程为

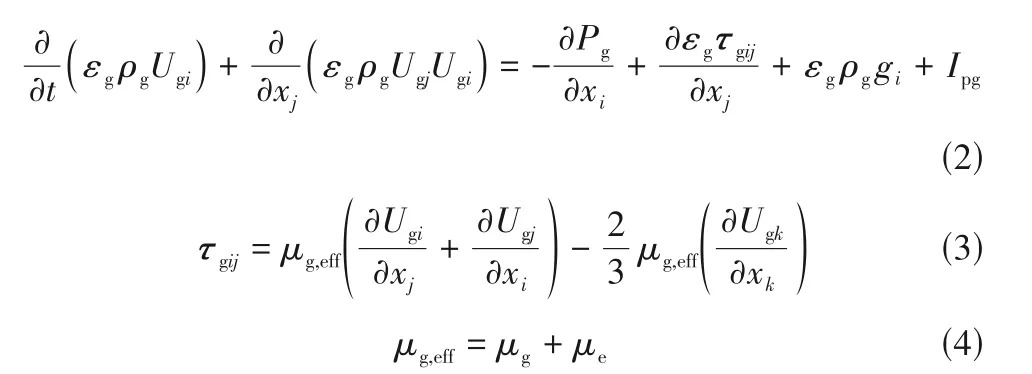
式中，Pg是气体压力；τgij为气相应力张量；gi为重力加速度；Ipg为气固相相互作用动量源项；气相密度ρg由理想气体方程求解；μg,eff为有效气体黏度，由式（4）计算得到；μg为气体分子黏度，由Sutherland方程[27]计算得到；湍流黏度μe采用标准k-eplison 模型[28]进行求解。

气相组分守恒方程为

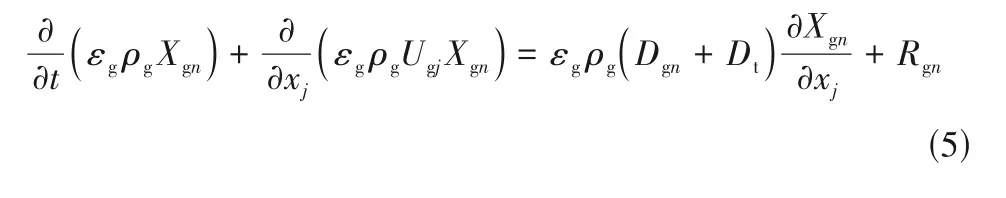
式中，Xgn表示气相组分n的质量分数；Rgn为化学反应源项；Dgn表示气相组分n的分子扩散系数，由FSG 关联式[29]计算得到；Dt为湍流扩散系数，由式（6）计算[30]。

式中，Sct为湍流Schmidt数，取0.9。

气相能量守恒方程为

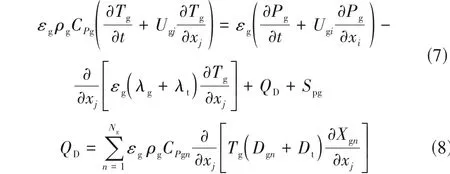
式中，Tg为气相温度；CPg、CPgn分别为气相混合比热容以及气相组分n的比热容；λg为分子传热系数；λt为湍流传热系数，由式（9）进行计算[30]，湍流Prandtl 数Prt取0.9；QD为气相组分焓扩散项；Spg为颗粒对流体的能量源项。式（7）中忽略了流体黏性耗散项，并且由于氢氯化反应速率较慢以及反应放热较小，床内气固相间温差较小，因此也忽略了气固相间的辐射传热。

1.1.2 颗粒相方程 颗粒的质量守恒方程为

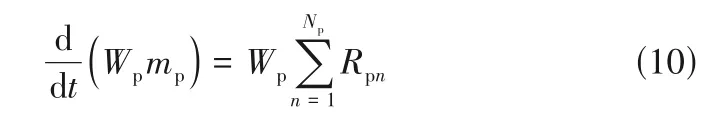
式中，Np为真实颗粒中的化学组分数；Wp为颗粒统计权重，即每个计算颗粒中包含的真实颗粒数；Rpn为真实颗粒中组分n的生成或者消耗速率。

颗粒的组分守恒方程为

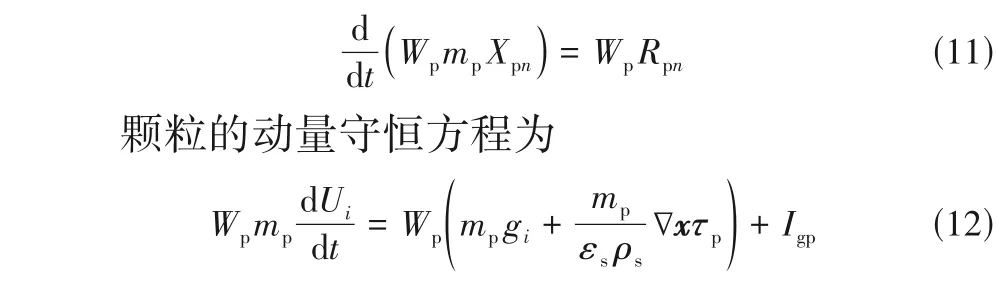
式中，Ui为计算颗粒在i方向的速度分量；τp为颗粒应力，由式（13）计算得到；Igp是流体对计算颗粒的动量传递项。

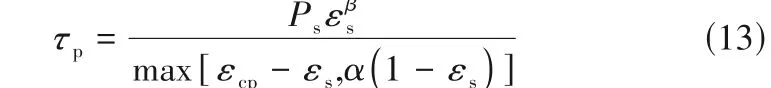
式中，εcp为固相堆积体积分数；εs为颗粒相体积分数；Ps为经验压力常数；β为无量纲指数；α为一非常小的常数，用于防止分母为零[30]。

颗粒空间位置的变化由式（14）得到。

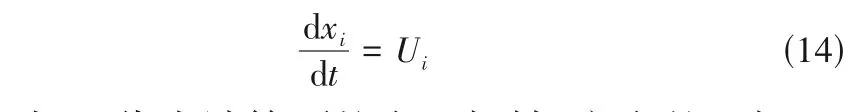
式中，xi代表计算颗粒在坐标轴i方向的坐标。颗粒的能量守恒方程为

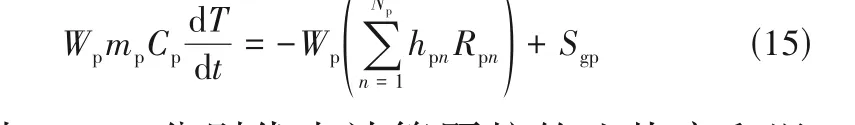
式中，Cp、T分别代表计算颗粒的比热容和温度；hpn为组分n的比焓；Sgp为流体对颗粒的能量源项。

1.2 相间作用力模型

流体对计算颗粒的动量交换项由式（16）定义。

1.3 相间能量传递模型

流体对计算颗粒之间的能量传递源项由简化表达式（17）定义[30]。

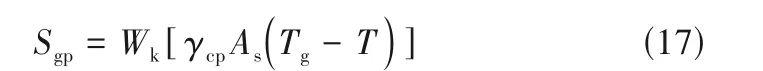
式中，γcp为对流传热系数；As为计算颗粒k中真实颗粒的表面积。对流传热系数由式（18）计算。

式中，Nu为Nusselt数；dp为真实颗粒的直径；λg为流体热导率。Nu由Ranz & Marshall 关联式[32]进行计算。

1.4 化学反应模型

根据丁伟杰[10]的研究，反应主要发生在颗粒附近，因此可将总反应视为气固反应，反应速率由总包动力学表达式[式（19）]进行计算[9,14]。其中的参数列于表1。模拟中假设反应器内催化剂分布均匀。

表1 反应动力学参数［9，14］Table 1 Parameters of kinetic equation［9，14］

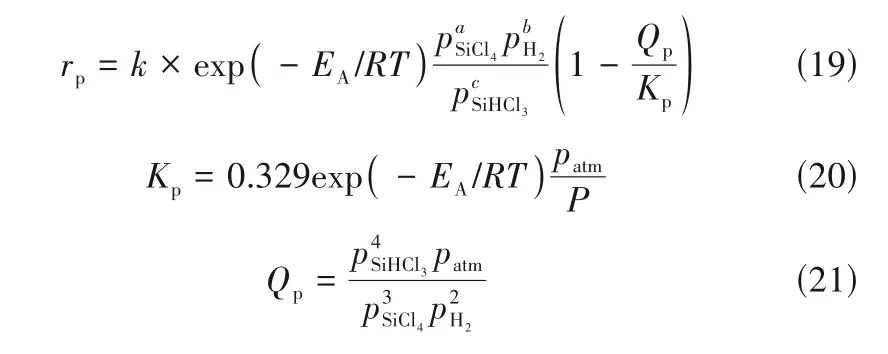
式中，pSiHCl3、pSiCl4、pH2、patm分别为各气相组分分压以及标准大气压。

1.5 计算方法

基于Sill 等[11,16]的实验，对实验流化床反应器进行模拟。鼓泡床状态下操作，如图1所示，流化床高度为0.400 m，内径为0.050 m，初始床层高度为0.165 m。数值计算过程在开源软件MFIX 中完成。所采用的实验数据列于表2。模拟的初始条件按实验条件或者根据分析的需要进行设置。对于边界条件，在流化床底部进口处设置为质量进口条件，流化床顶部出口设置为压力出口条件。对于壁面条件，气相采用壁面无滑移条件，颗粒相与壁面作用采用不完全弹性碰撞。壁面绝热，没有质量流入。相应的模拟参数列于表3。

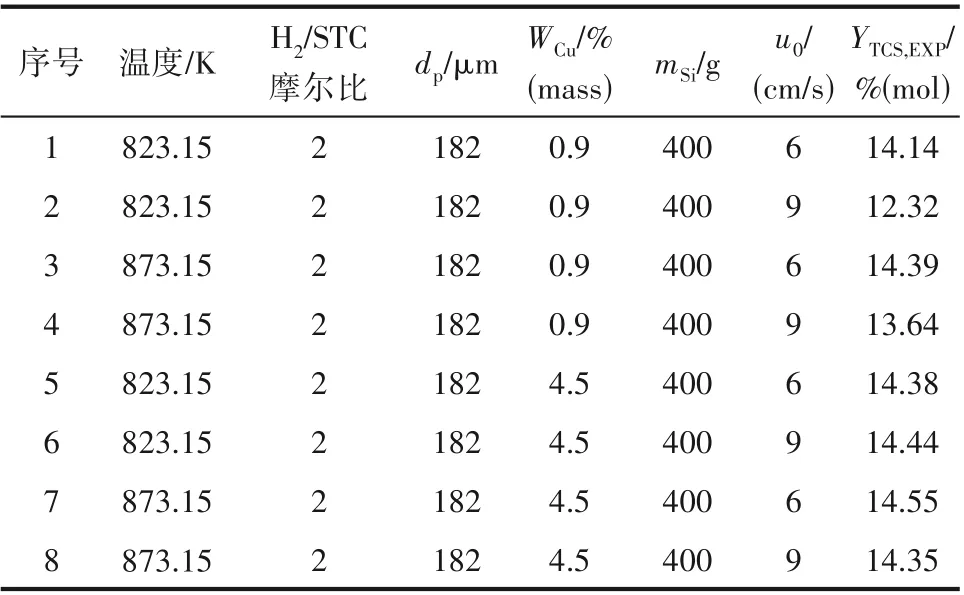
表2 实验数据Table 2 Experimental data

表3 模拟参数Table 3 Parameters for simulation

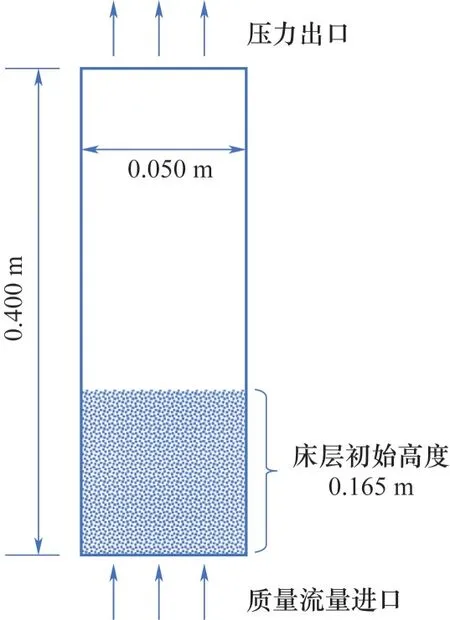
图1 流化床反应器示意图Fig.1 Sketch of fluidized bed reactor

2 计算结果与分析

2.1 无关性分析

2.1.1 网格以及计算粒子所包含的颗粒数无关性

基于表2 中第2 组实验条件，在不考虑反应、传热和传质的前提下，对网格以及计算颗粒包含的真实颗粒数量进行无关性检验以确定相应的合理值。采用cell-cut 方法[33]对圆柱进行划分。采用15×115×15、20×155×20、25×190×25三种方式进行划分，相应的网格大小分别为3.3 mm×3.5 mm×3.3 mm、2.5 mm×2.6 mm×2.5 mm、2.0 mm×2.1 mm×2.0 mm。图2给出了计算Wp为200 时，采用三种不同网格划分方式计算得到的时均气相相分率轴向分布情况。对比可知，三种网格划分方式得到的计算结果较为接近。基于20×155×20 网格划分方式，对Wp值的大小进行检验。图3 给出了Wp值分别为100、200、400时，计算得到的时均气相相分率轴向分布情况。结果表明，Wp值变化对计算结果的影响可以忽略。综合考虑计算量以及计算精度，选择采用20×155×20的网格划分方式，Wp值设置为200。

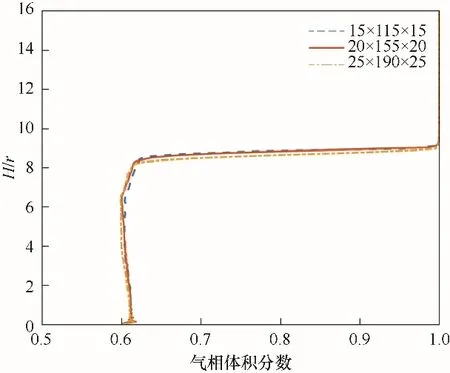
图2 采用不同网格划分方式得到的时均气相相分率轴向分布Fig.2 Axial distribution of time-averaged gas phase fraction for different grids

图3 采用不同计算颗粒包含的真实颗粒数量得到的时均气相相分率轴向分布Fig.3 Axial distribution of time-averaged gas phase fraction for different number of particle per parcel

2.1.2 TCS初始浓度无关性 由于模拟中采用总包反应动力学对反应器进行模拟，反应动力学模型的计算要求必须设置反应器内三氯氢硅（TCS）初始浓度。为了考察TCS 初始浓度对于计算结果的影响，基于表2中1号实验数据，采用表4所示三组不同的气相组分浓度作为初始值进行计算。图4给出了不同TCS初始浓度计算得到的出口TCS摩尔分数随流动时间变化情况。从图中可知，虽然初始浓度不同，随着流动进行，出口TCS摩尔分数趋于一致。图5 给出了30 s 时反应器内轴向平均温度分布情况。结果表明，不同TCS 初始浓度计算得到的反应器内轴向温度分布较为接近。TCS初始浓度无关性检验表明，当TCS初始浓度较高时，反应逆向进行。虽然此时反应吸热，但是由于吸热量较少，温度变化较小。这使得初始浓度下的温度分布不会对之后的反应造成较大影响。反之，当TCS初始浓度较低时，反应正向进行引起的温度升高量也同样较小，进而对后续反应的影响同样较小。

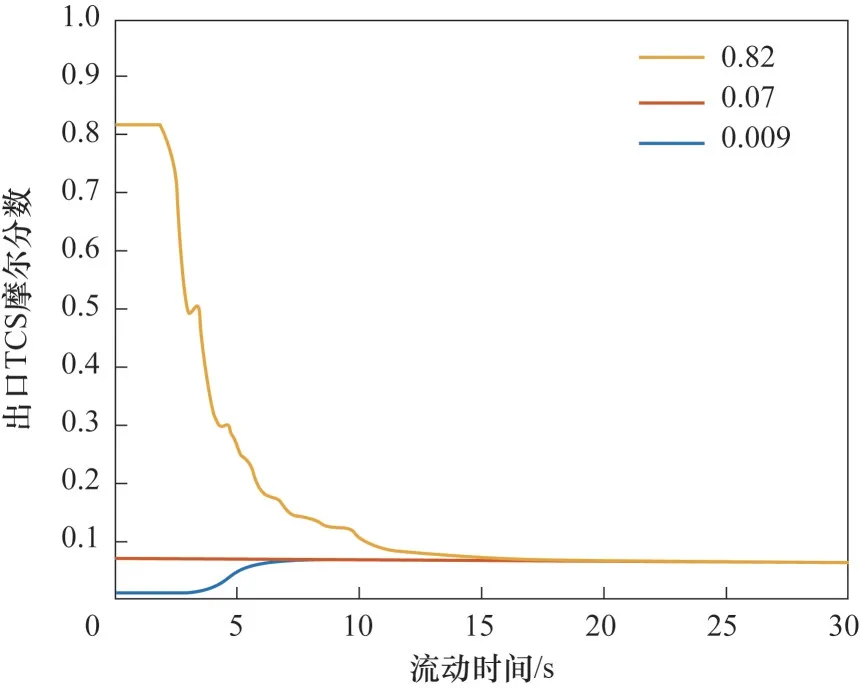
图4 不同TCS初始浓度条件下出口TCS摩尔分数随流动时间变化情况Fig.4 Change of outlet TCS molar fraction with flow time under different initial concentration of TCS

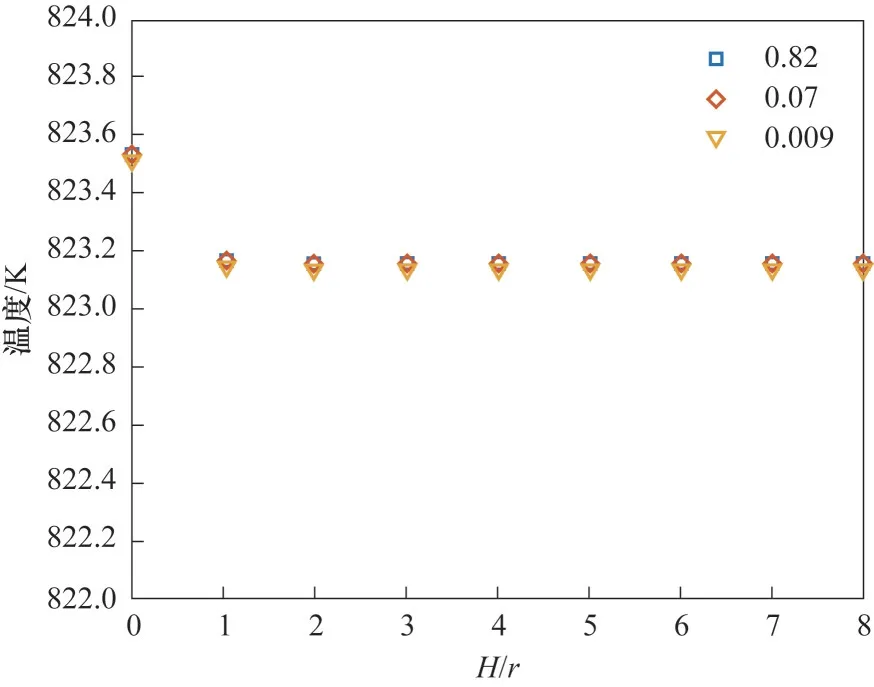
图5 不同TCS初始浓度条件下反应器内轴向平均温度分布情况Fig.5 Axial average temperature distribution in the reactor under different initial concentration of TCS

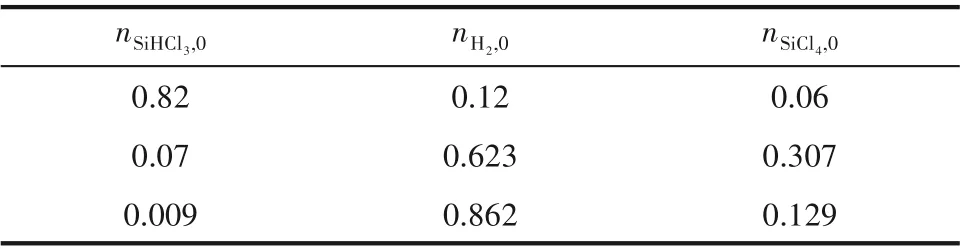
表4 TCS初始摩尔分数Table 4 Initial mole fraction of TCS

2.2 模拟结果验证

基于以上无关性分析，对表2 中的实验条件进行模拟。TCS产率由式（22）计算。

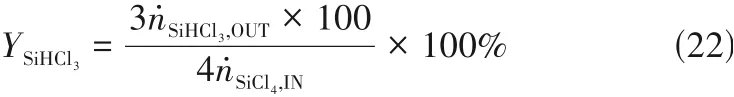
式 中，ṅSiCl4,IN和ṅSiHCl3,OUT分 别 为 反 应 器 进 口 处STC 摩尔流率以及出口处TCS 摩尔流率。图6 给出了TCS 产率的模拟结果与实验值之间的对比，包括Colomb等[14]对该反应器的模拟结果。模拟值与实验值的相对误差由表5 给出。结果表明，与Colomb等[14]的模拟结果相比，本文采用的计算模型同样具有相当的精确度。其中，第1、2、5、6 组计算得到的TCS 产率与实验值更为接近；而在第3、4、7、8 组中，计算得到的产率稍高。导致这一现象的原因可能是模拟中采用的催化剂均匀分布假设在较低进口表观气速时与实验情况较为符合，在较高的进口表观气速下与实验情况存在一定差异。但是，这种差异在本文的研究范围内是可以接受的。

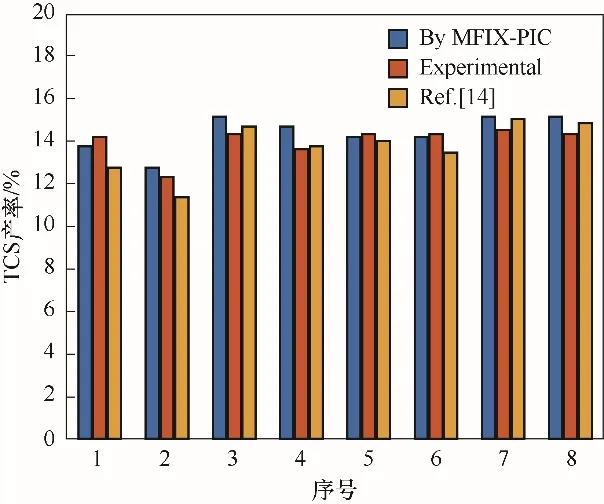
图6 计算得到的TCS产率与文献模拟值[14]以及实验值对比Fig.6 Comparison of simulated TCS yield with simulated results[14]and experimental results

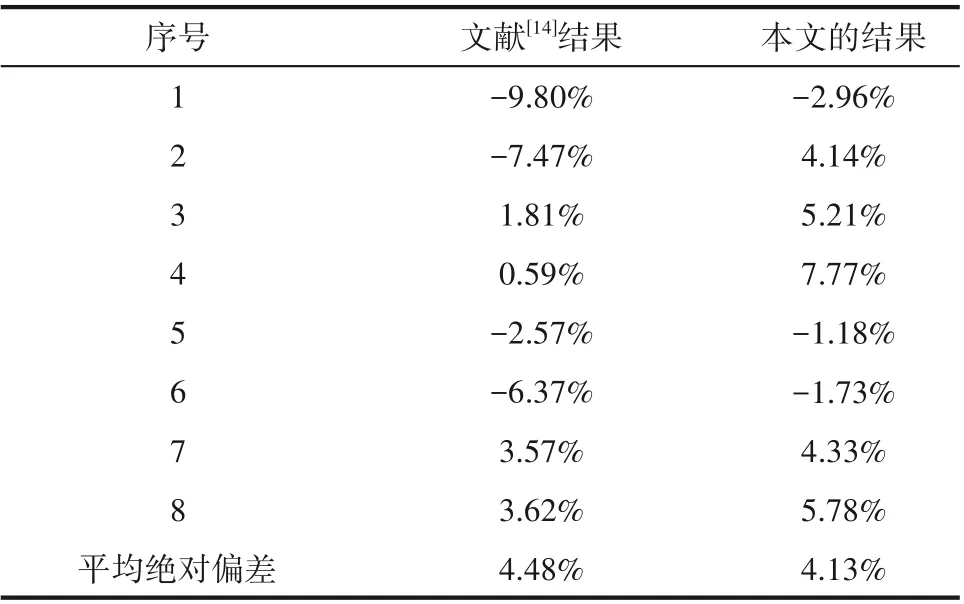
表5 模拟值与实验值的相对误差Table 5 Relative error between simulated results and experimental results

2.3 反应与流动特征分析

基于表2 中第1、2、4、6 组实验条件模拟结果对反应过程中流动与反应特征进行分析。图7 和图8分别给出了相应的轴向平均表观气速以及压力分布情况。从图中可见，虽然反应会使得气相摩尔流率减小，但是轴向平均表观气速分布仍较为均匀。这是由于反应转化率较低。按照实验转化率计算，气体体积减小的比例仅为2%左右，而由于床层压降引起的气相压力减小所导致的气相体积膨胀可以弥补由反应减小的气相体积。因此，反应对轴向平均表观气速的影响可以忽略，轴向平均表观气速可以视为不变。

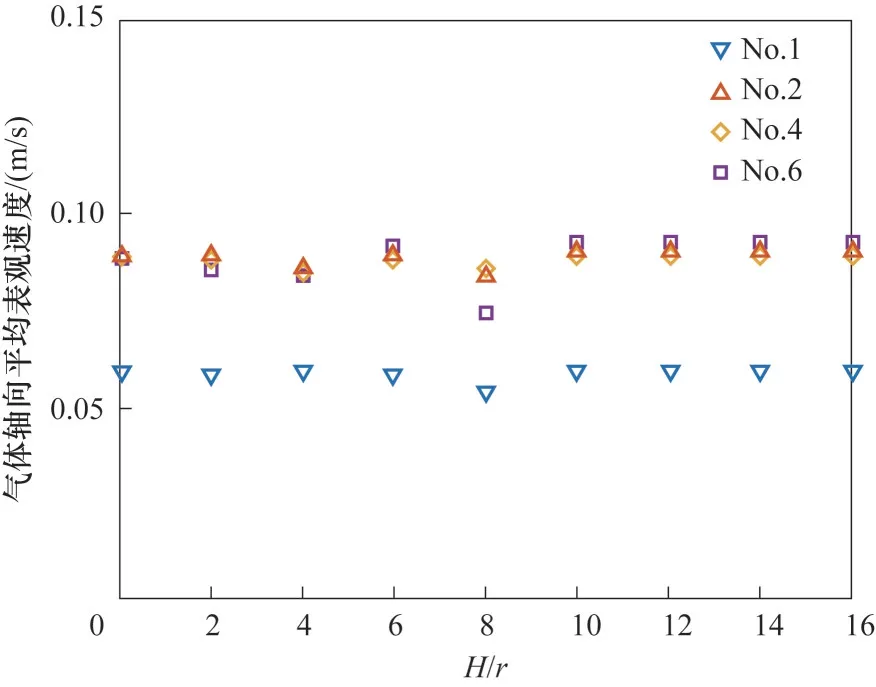
图7 30 s时反应器内轴向平均表观气速分布Fig.7 Axial average apparent gas velocity distribution in the reactor at 30 s

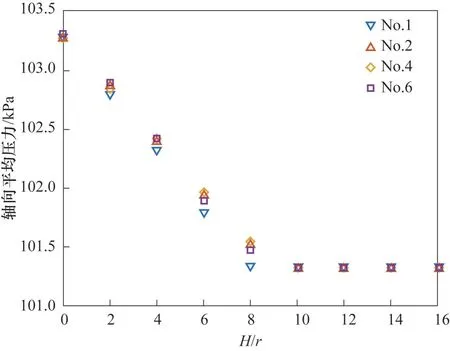
图8 30 s时反应器内轴向平均压力分布Fig.8 Average axial pressure distribution in the reactor at 30 s

已知反应受平衡限制，引入Qp∕Kp值作为判断反应远离平衡程度的指标，对不同操作条件下反应器内反应特征进行分析。图9 和图10 分别给出了不同条件下，时均Qp∕Kp值分布情况以及对应的气相相分率分布情况。对比图9（a）、（b）可知，在较低的进口表观气速下，气相组分沿径向分布较为均匀，主要表现为平推流。同时，从图10中可以发现，在较低的表观气速下，气固相分布较为均匀[图10（a）]。进口表观气速增加对床内流动的影响主要表现在颗粒床层高度略增加，而对床内气固相间空间分布的均匀性影响较小。相比床层高度增加，进口表观气速的增加更加明显，由此导致反应气体在床内的停留时间缩短。同时，由速率常数k的量纲可知，反应物的反应级数大于1，由较高的表观气速引起的气相组分返混会使得TCS的产率进一步降低。

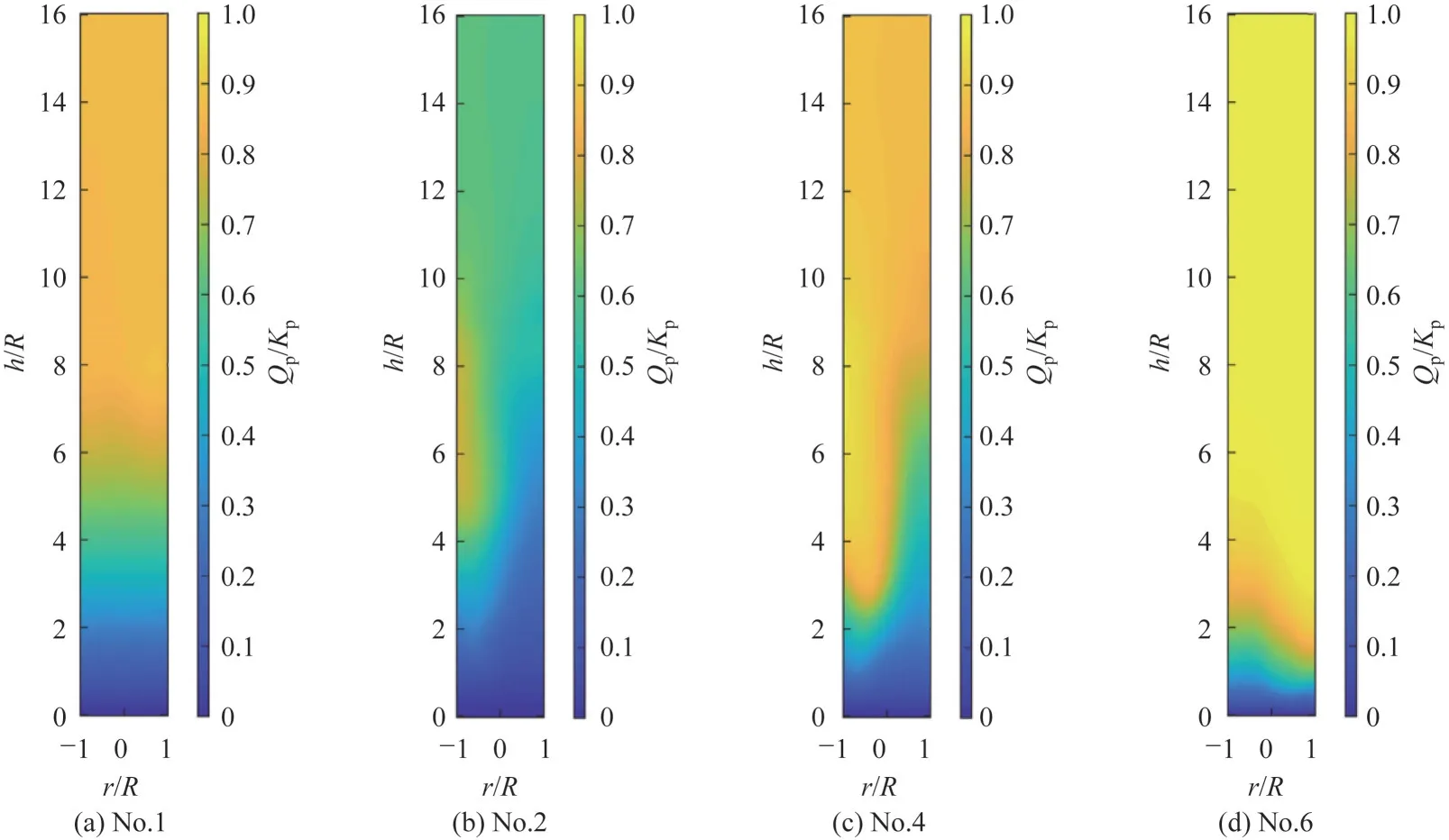
图9 流化床反应器中时均Qp∕Kp值分布情况Fig.9 Distribution of time-averaged Qp∕Kp value in the simulated fluidized bed reactor

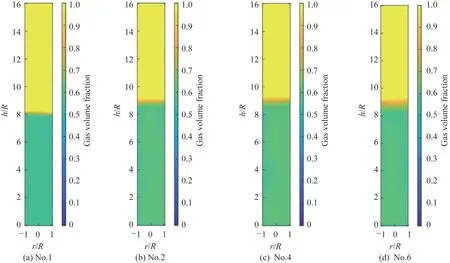
图10 模拟流化床反应器中时均气相相分率分布情况Fig.10 Distribution of time-averaged gas volume fraction in simulated fluidized bed reactor

对比图9（b）～（d）可知，升高反应温度或者增加催化剂量均可以加快反应速率从而提升转化率。从图9（c）、（d）中可以发现，反应在气相反应物进入床层一段距离后已经接近平衡，这使得在床层上部，反应几乎不再进行。因此，由表观气速引起的短路以及返混的影响可以忽略。这里值得说明的是，与添加催化剂不同，升高反应温度会提高反应平衡常数，但是由于温度对反应速率的影响更大，因此升高温度会使得反应过程更接近平衡。由图10（b）～（d）可以发现，由于反应转化率受到限制，在反应消耗以及压差共同作用下，反应器内表观气速相差较少，因而增加反应速率对于床内的相分率分布的均匀性影响很小。

综合以上讨论，对于实验级的冶金硅氢氯化反应器而言，化学平衡与气固流动是反应产率的共同控制因素。当反应器内反应离化学平衡较远时，反应转化率由流动控制，在本文的研究中，流动因素主要表现为气相在床层中的停留时间；而当反应器内的反应接近平衡时，反应转化率由化学平衡控制。在反应器设计与优化过程中应该综合考虑这两种因素的影响。

2.4 操作条件分析

基于以上分析，在Sill 等[11,16]对冶金硅流化床反应器的实验研究基础上，进一步对操作压力以及进口H2∕STC摩尔比对TCS产率的影响进行探究。

2.4.1 压力对TCS 产率的影响 图11 中给出了不同操作压力下TCS产率的变化情况。从图中可以发现，在实验级流化床反应器中，压力对于产率的影响较小。从动力学表达式中可以发现，压力虽然可以改变平衡常数大小，但是不改变Qp∕Kp值。在相同的条件下，反应速率的增大倍数为压力增加倍数的1.086 次方。对于较低表观气速操作而言，反应已经接近平衡，增加操作压力，对反应产率的提高不明显。对于较高表观气速操作而言，随着压力增加，TCS产率逐渐接近较低表观气速下的产率。

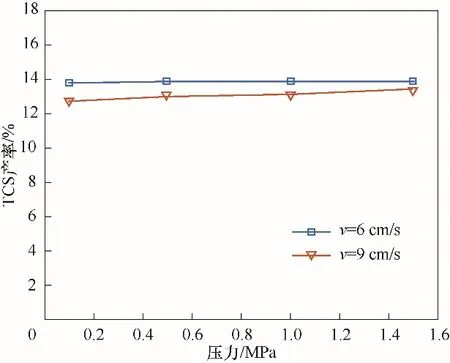
图11 不同进口表观气速下操作压力对TCS产率的影响Fig.11 Effect of operation pressure on TCS yield under different inlet apparent gas velocity

2.4.2 进口H2∕STC 摩尔比对TCS 产率的影响 图12 中给出了TCS 产率随H2∕STC 摩尔比变化情况。由Le Chatelier 原理可知，对于可逆反应而言，当反应平衡时，提高一种反应物的浓度可以增加另一种反应物的转化率。因此，对于受化学平衡限制的冶金硅氢氯化反应器而言，增加进口H2∕STC 摩尔比，可提高TCS产率。

此外，从图12 中可以观察到，随进口H2∕STC 摩尔比变化，进口气速对于TCS产率的影响发生变化。在进口H2∕STC 摩尔比较低时（H2∕STC 摩尔比＜2），反应可快速接近平衡，因此，流动因素对于TCS产率的影响不大。但随着进口H2∕STC 摩尔比的增加，反应逐渐远离平衡，反应转化率逐渐转为流动控制，停留时间成为主要的控制因素。因此，在相同的进口表观气速下，TCS 产率增加速率减缓。需要指出的是，虽然提高进口H2∕STC 摩尔比有利于TCS 产率的增加，但却降低了H2的利用率，需要进行全局考虑。

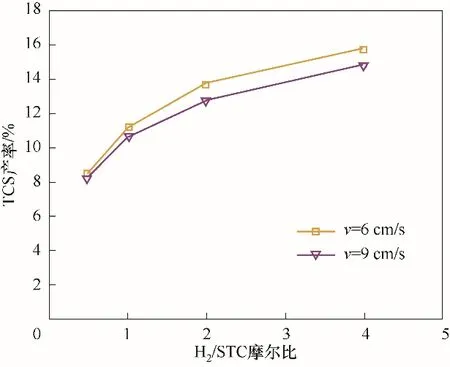
图12 不同进口表观气速下进口H2∕STC摩尔比对TCS产率的影响Fig.12 Effect of inlet H2∕STC molar ratio on TCS yield at different inlet apparent gas velocity

3 结 论

本文基于MP-PIC 方法采用总包反应动力学模型对实验级冶金硅氢氯化反应器进行模拟。对TCS初始浓度进行无关性检验，结果表明由于反应弱放热且转化率较低，TCS 初始浓度对于反应器模拟结果几乎没有影响。根据实验条件模拟得到TCS产率与实验值吻合良好。对反应器内流动与反应特征以及不同操作条件下的计算结果进行分析得到以下结论。

（1）虽然在冶金硅氢氯化反应中气相物质的量会减少，但是由于反应器内反应物转化率较低，由床层压降引起的气相压力降低可以弥补由气相分子数减少引起的气相体积变化。

（2）在反应器内，反应过程同时受到流动因素与化学平衡因素控制。当反应尚未接近平衡时，流动因素对TCS 产率起控制作用；当反应已经接近平衡时，流动因素对反应产率不起作用，转而由化学平衡控制。

（3）提高操作压力虽然可以加快反应速率，但是对于TCS 产率的影响不明显。通过增加进口H2∕STC 摩尔比可以使得反应远离平衡进而提高TCS 产率，但是会降低H2的利用率。

符 号 说 明

a,b,c——反应动力学参数

EA——反应活化能，kJ∕mol

H——床高，m

Kp——化学平衡常数

k——速率常数，mol∕(kg·s·Pa1.086)

mSi——冶金硅颗粒加载量，g

P——气相总压，Pa

Qp——反应熵

R——气体常数，J∕(mol·K)

r——流化床半径，m

rp——反应速率，mol∕(kg·s)

T——反应温度，K

u0——进口表观气速，cm∕s

WCu——催化剂质量占冶金硅颗粒总质量百分比，%

Wp——每个计算颗粒中包含的真实颗粒数

YTCS,EXP——三氯氢硅产率，%