基于二维梯度树状肋相变储热系统强化传热机理

张欣宇，杨晓宏，2，张燕楠，徐佳锟，郭枭，田瑞，3

（1 内蒙古工业大学能源与动力工程学院，内蒙 古呼和浩特 010051； 2 风能太阳能利用技术教育部重点实验室，内蒙古呼和浩特 010051； 3 内蒙古可再生能源重点实验室，内蒙 古呼和浩特 010051）

引 言

在能源应用中，太阳能由于清洁无污染、绿色环保、辐射能流高、可再生而在全球广泛应用，但其应用受到季节、阴雨、昼夜更替等自然条件影响。为解决太阳能在时间、空间上不匹配的问题[1-2]，采用储能技术将暂时不用或多余的太阳能以热能的形式存储起来[3-4]。相变储热在合适的温度范围内具有较高的能量存储密度，且过程近乎恒温，具有良好的热稳定性，被广泛应用[5-7]。但相变材料（phase change material,PCM）的导热性能差[热导率普遍低于0.5 W∕(m·K)]，直接影响了相变储热系统能量存储密度和传热速度[8]。研究发现，强化相变储热系统可以改变相变储热系统的结构，通过肋片增大传热流体（heat transfer fluid,HTF）与PCM 的换热面积[9-11]；同时也可以制备高热导率的复合相变材料，通过向基础相变材料中添加金属粒子或高导热性能的骨架[12-13]实现热流体与相变材料的传热强化。

通过合理的肋片设计来提高相变储热系统温度分布的均匀性是强化传热的有效途径[14-15]。Khan等[16]研究了水平潜热储能单元中肋片方向对强化传热的作用。基于焓孔隙率方法，对具有纵向肋片的管壳式相变储热系统的二维瞬态模型进行数值计算，通过改变翅片的不同角度（0°≤θ≤90°）进行了研究。Yu 等[17]设计了梯度肋片相变储热系统以提高熔化性能。建立了熔化传热过程的二维模型，分析了熔融前沿演化和动态温度分布，研究了自然对流、翅片布局和Stefan 数的影响。通过响应面法以完全熔化时间为目标函数对翅片布置进行优化。结果表明，自然对流严重影响了相变储热装置的熔化行为。Liu 等[18]为使相变储热系统的温度更均匀、熔化速度更快，应用数值模拟方法优化了不均匀的树状肋片，研究填充角和中心角梯度在熔化过程中的作用，结果表明，不均匀的树状翅片显著提高了储能性能，因为热传导增强超过了自然对流抑制。与传统的树状翅相比，通过储热系统中自然对流和热传导的协同改进，不均匀的树状翅片使温度分布更均匀和熔化速度更快。Safari 等[19]将树形翅片布置在水平放置相变储热（latent heat storage,LHS）单元的下部PCM 中，结果表明，与均匀的树形翅片相比，非均匀设计将熔化过程缩短了9.25%。然而，非均匀翅片布局仅考虑下层PCM 的传导增强，上层PCM 的熔化过程由于缺乏有效的传热路径而减慢。Huang等[20]研究树形翅片的LHS 单元均匀布置和梯度布置两种方式。通过可视化实验结合三维数值模拟，对LHS 单元的熔化∕凝固热性能进行综合分析。结果表明，树状翅片有利于热从点到面的扩散，打破了传统LHS 单元的传热滞后，从而加快了熔化∕凝固速度。在熔化过程中，梯度树形翅片加强了热能存储（thermal energy storage, TES）单元下部的传热，延长了上部区域的对流传热持续时间，促进熔融后期自然对流和热传导的协同强化。与均匀翅片布局相比，梯度树形翅片有效提高了熔化速度，将熔化持续时间缩短了9%。然而，梯度树形翅片的非均匀传输路径不利于以热传导为主的凝固传热，与均匀树形相比，LHS 单元的温度梯度增加，凝固时间延长了57.4%。

当前，研究主要从树状翅片结构、布局分析传热过程[21-22]，相变储热系统蓄释热整个传热过程深入的机理分析较少，部分研究者仅考虑将热能储存起来，忽略了释热过程的重要性，未深入分析自然对流与热传导在蓄释热过程中的协同作用。因此，本文基于二维梯度树状肋相变储热系统分析其传热特性，考虑到温度分布的均匀性，采用场协同理论[23-25]分析温度场和速度场的协同特性[26-28]，对相变材料的熔化和凝固过程的传热机理进行综合分析，分析相变材料熔化温度对蓄释热的影响，为相变材料的选择提供理论依据。

1 模型的建立

1.1 物理模型

图1为水平放置的三种相变储热装置的二维模型。外管选择铝管，内直径为124.0 mm，厚度为3.0 mm；内管选择铜管，内直径为45.0 mm，厚度为2.5 mm。内管与外管同轴，周向均匀布置六根相同的梯形翅片，肋片管材为铜，Case 1为均匀分布的六纵肋储热模型，Case 2 为在Case 1 模型基础上增加了次肋的雪花型肋储热模型，Case 3 为在Case 2 基础上采用梯度布置的树状肋储热模型。HTF 流经管内，PCM 填充在管外和壳体之间的空隙中。HTF 沿轴向方向温度梯度变化与径向方向的温度梯度相比较小，传热特性主要与管子径向方向有关，因此可以将三维传热模型简化为二维的传热模型[16]。考虑到应用的可靠性及储热特性，PCM 选择石蜡，HTF选择熔融盐，基础材料的热物性如表1所示。

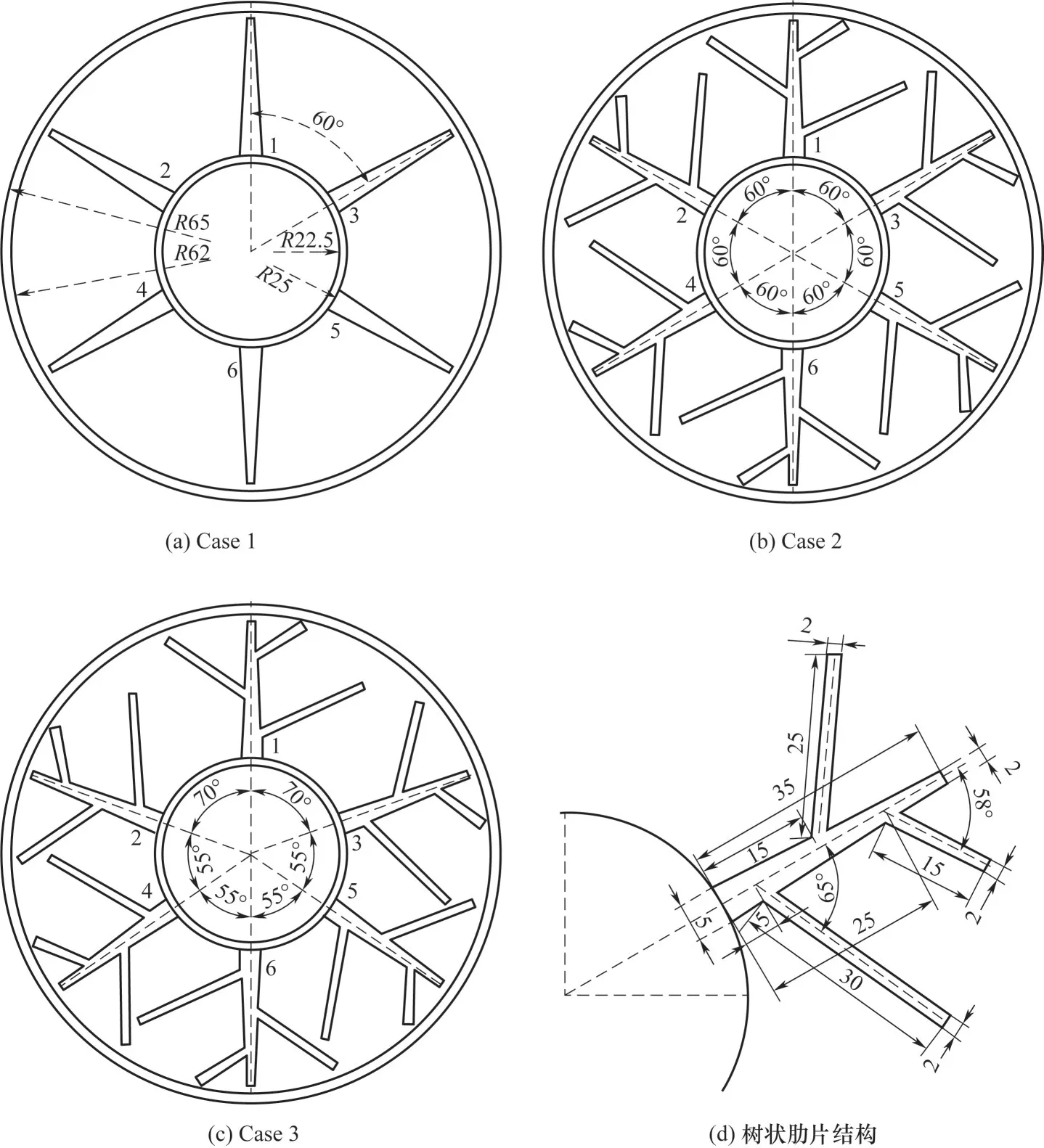
图1 三种相变储热模型及尺寸Fig.1 Three-phase change heat storage models and dimensions

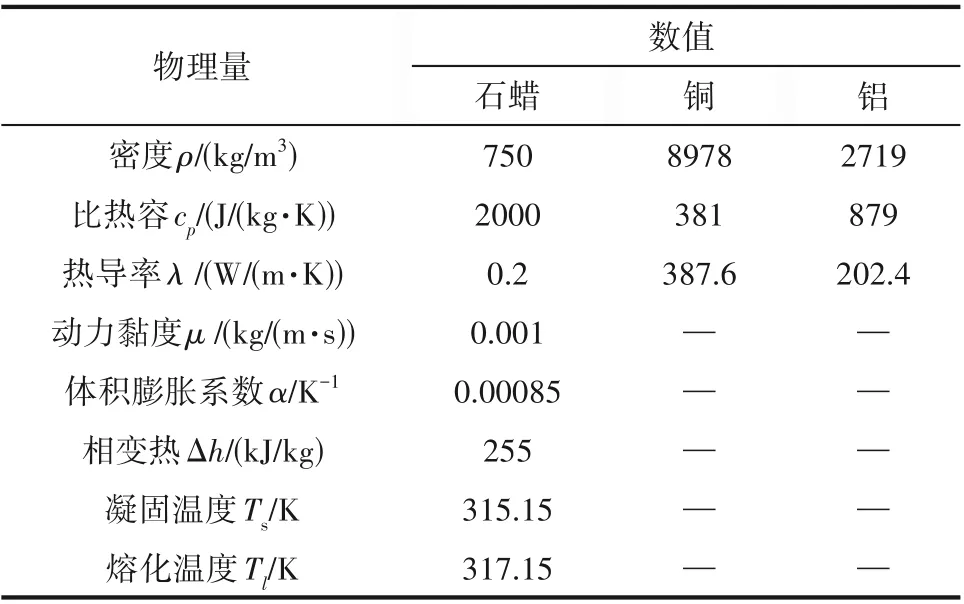
表1 PCM及铝和铜的热物理性质［29］Table 1 Thermophysical properties of PCM，aluminum and copper［29］

1.2 数学模型

为简化计算过程，对相变储热系统PCM 的熔化和凝固过程做如下假设：（1）传热问题是二维非稳态的；（2）液体PCM 被认为是不可压缩的牛顿型流体，均质且各向同性；（3）储热系统初始温度均匀且外壁是绝热的；（4）液体PCM 的自然对流为层流[30]；（5）PCM 熔化过程中由于温度变化引起密度变化使得浮升力作用下的传热服从Boussinesq 近似建模，在除浮力项外的所有项中密度均为常数；（6）PCM包括液相、固相和糊状相；（7）液固界面处的两相保持热平衡；（8）HTF 以恒定质量流量和恒定的温度进入管内。

在边界条件方面，设置管内壁为等温边界条件[31]。管外及肋片与PCM 为流固耦合界面，储热罐外壁绝热。因固液相变材料之间存在密度差，需要考虑重力引起的自然对流换热，在Y轴方向开启重力项，模型区域初始化定义，蓄热过程相变材料及肋片管初始温度为300.00 K，管内壁温度设置为380.00 K[17]；释热过程相变材料及肋片管初始温度为380.00 K，管内壁温度设置为300.00 K。

1.3 数值分析方法

本模拟采用Fluent19.2 软件，相变过程引入焓-孔隙率方法进行数值求解建模。采用二维焓-孔隙率法数值求解该问题，已有文献指出该方法的结果与复杂的三维流体体积法的结果准确匹配[32]。采用SIMPLE 算法基于压力-速度耦合的双精度求解器，选择压力交错选项PRESTO 用于自然对流，动量方程和能量方程的对流项采用二阶迎风格式离散。为了更好地收敛，密度、压力、动量和能量的欠松弛因子分别设置为1、0.3、0.5 和0.8。此外，当对应的连续性方程、动量方程及能量方程的最大残差依次小于10-3、10-6、10-8，认为迭代是收敛的。

1.4 场协同理论分析传热过程

从对流换热的场协同理论分析，对流传热系数是由整个对流区域中各种场参数相互作用的结果。对流传热的强度不仅取决于流体与固壁的温差、流动速度、流体的热物性和输运性质，而且还取决于流体速度场与热流场的协同程度。因此，引入场协同数

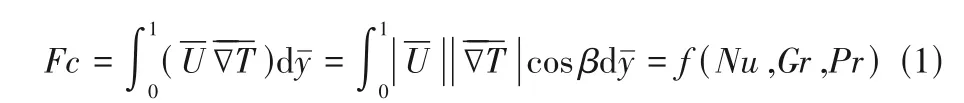
式中，Fc反映速度场和热流场的协同程度（Fc≤1），当Fc=1时对流换热的速度场和热流场达到完全协同，此时，速度场与热流场配合最好，即协同程度最高，同时也是换热强度可能达到的最大值；-U为无量纲速度；∇T为无量纲温度梯度；β为流体流动方向与热流传递方向的夹角，两矢量的夹角尽可能小（β＜90°）或尽可能大（β＞90°）都能强化传热；速度矢量和热流矢量的夹角的余弦总是趋于零（cosβ→0），使得Fc≪1，因此通过提高速度场与温度梯度场的协同可以强化换热。

场协同数还可以表示成关于准则数的函数形式，其中Nusselt 数Nu为壁面上流体的无量纲温度梯度，表征对流换热的强弱；Grashof 数Gr判断PCM熔化过程的流态；Prandtl数Pr是动量扩散与热量扩散之比，表征流体的热物理性能，具体表达式为式（2）～式（4）。

式中，h为对流传热系数，W∕(m2·K)；tw为翅片内管壁温，380.00 K；t0为初始PCM 温度，300.00 K；δ为PCM 填充沿径向最大厚度，0.037 m，按照小空间自然对流换热计算；运动黏度v=μ∕ρ，1.333×10-6m2∕s；a为热扩散率，m2∕s；g为重力加速度，9.8 m2∕s；α为体积膨胀系数。本研究取翅片管壁温与初始PCM 最大温差为80℃，经计算Gr为1.8987×107，对于水平放置的储热系统，Gr在1.43×104～5.76×108为层流流动。

2 数值分析方法模型验证

2.1 网格大小和时间步长独立性验证

利用结构化网格对二维截面进行网格划分，如图2所示，由四边形网格和三角形网格组成。Case 2模型的熔化过程中，不同网格和时间步长PCM 液相率及温度变化如图3 所示。网格A、网格B、网格C节点数依次为12614、20480、34690，网格B 与网格C的温度曲线几乎重合，网格A 与网格B 的最大偏差为3.11%，网格B 与网格C 最大偏差仅为1.14%。时间步长0.05 s 和0.1 s 时的液相率具有很好的一致性，最大偏差仅为0.19%，与0.1 s 相比时间步长0.2 s 液相率最大偏差为1.84%。本研究选择节点数20480，时间步长0.1 s。

图2 计算域的网格图Fig.2 Grid system of the computational domain

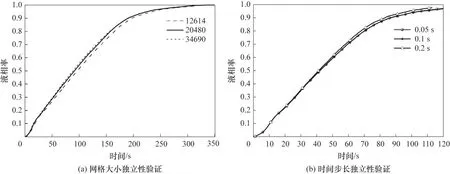
图3 网格大小和时间步长独立性验证Fig.3 Verification of grid size and time step independence

2.2 模型准确性验证

为验证数值方法的有效性，将数值结果与Al-Abidi 等[33]的实验结果进行比较，对三联管换热器（TTHX）的熔化进行了模型验证。采用上述数值分析方法，选择与文献[33]相同的几何模型和边界条件。PCM 初始温度为300.00 K。蓄热开始，TTHX 内管壁由温度为363.00 K 的HTF 加热。如图4 所示，内管、中管和外管的半径分别为25.4 mm、75.0 mm、100.0 mm，当前模型PCM 平均温度与实验平均温度比较，模拟数值与文献的实验数值吻合较好。实验与模拟之间的最大相对误差为2.11%，这是由于实验测量不可避免的误差，模拟过程进行了多条假设忽略了物性随温度的变化及固体下沉等因素，此误差在允许的范围内。因此，本文采用的数值模拟方法是有效的。

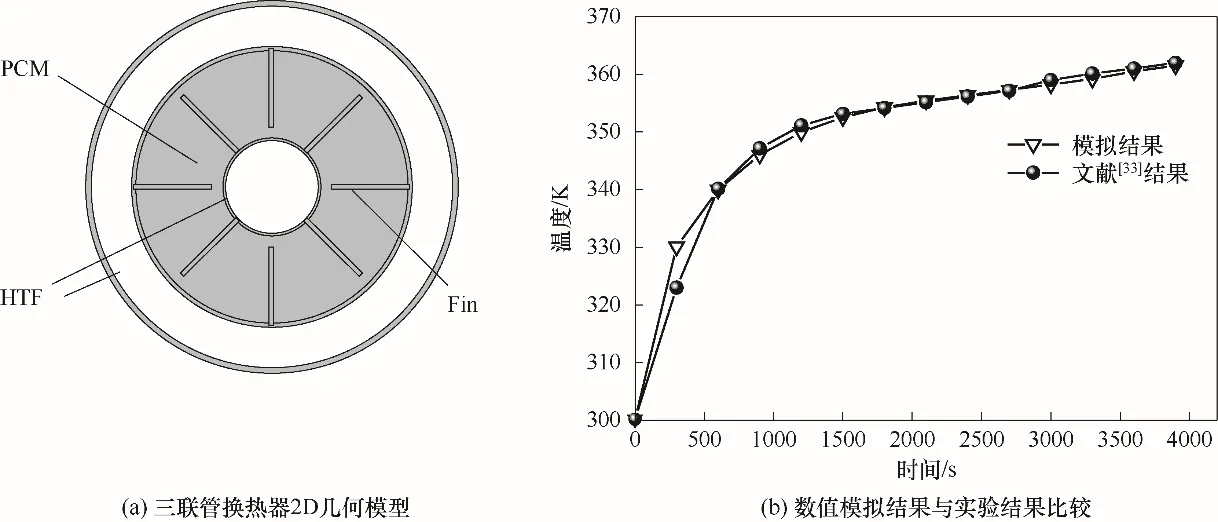
图4 数值方法的验证Fig.4 Validation of numerical method

3 结果分析

3.1 相变材料蓄释热过程云图分析

3.1.1 蓄热过程云图分析 如图5 所示，三个模型石蜡具有相同的熔化规律。初始阶段，靠近管外壁及肋片附近区域的石蜡温度先升高优先熔化，热量的传递逐渐向外壳扩散，距离较近的区域仍处于低能区，这是由于石蜡的低热导率使固态石蜡中的传热不利导致的，此时，热传导是传热的主要方式，对

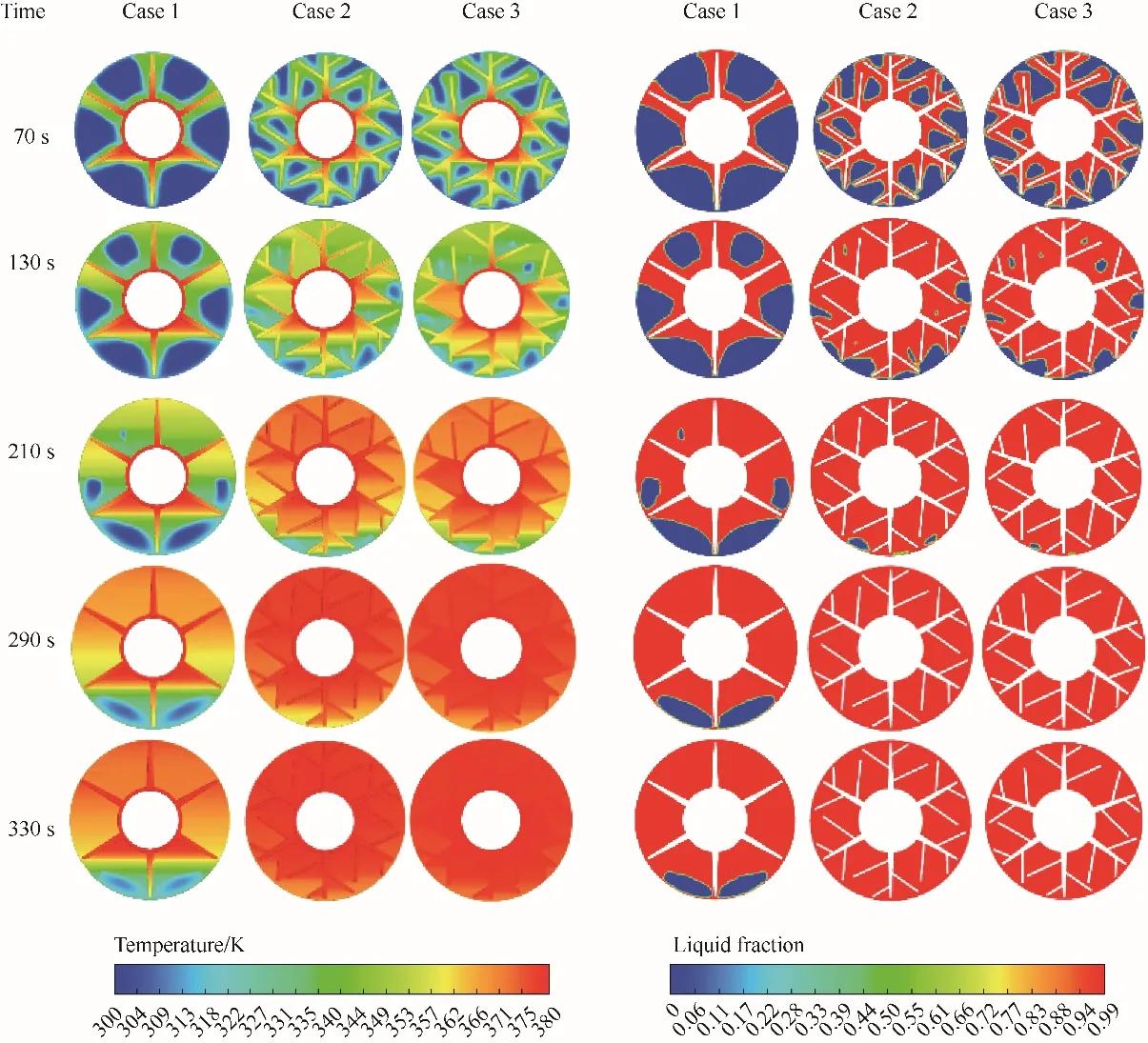
图5 三种模型石蜡熔化过程温度及液相率云图Fig.5 The cloud atlas of temperature and liquid fraction of paraffin melting process of three models

流换热是微弱的。由于加热管壁和相邻石蜡之间存在较高的热流量，焓的显热和潜热被迅速吸收，因此，石蜡经历了从固态—固液混合—液态的相变。随着围绕加热管壁的液体石蜡的增加，在重力的作用下浮力驱动的自然对流使高温低密度的液体石蜡产生向上的流动。高温液体石蜡在壳体顶部区域的积累增加，与下部区域相比，吸热量更高，此时自然对流换热为传热的主要方式。随着熔化的结束，液体石蜡在顶部区域的拥塞和较弱的流动性导致热量传递减弱，热传导是换热的主要方式。从云图可知，Case 1 的石蜡熔化过程上部明显比下部快，330 s 时仍有少量石蜡未熔化；Case 2、Case 3的熔化规律基本相同，这是由于在Case 1 的主肋上增设次肋进一步强化了传热，使熔化更均匀，290 s时石蜡全部熔化。可见，石蜡熔化过程是自然对流和热传导协同作用的结果。

3.1.2 释热过程云图分析 如图6 所示，在凝固初期，靠近肋片及管外壁的石蜡首先凝固，随着非稳态过程的进行，释热的传递向外部扩散，石蜡放出热量温度降低，到达固相温度开始凝固，100 s 石蜡未开始凝固，由初温380.00 K 迅速下降，1200 s 时出现明显的凝固。与熔化过程相比，石蜡在整个凝固过程所需时间较长，这是由于石蜡的热导率低，凝固过程中热传导为主要的传热方式，对流换热是极其微弱的[34]，因此，凝固过程温度分布均匀。3600 s时Case 2、Case 3 石蜡全部凝固，Case 1 仍有部分石蜡未熔化。可见，在石蜡的凝固过程中热传导是换热的主要方式。

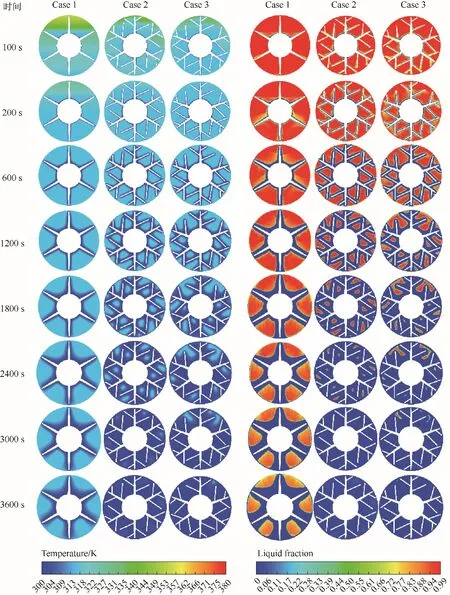
图6 三种模型石蜡凝固过程温度及液相率云图Fig.6 The cloud atlas of temperature and liquid fraction of paraffin solidification process of three models

3.2 相变材料蓄释热全过程传热特性分析

三种模型石蜡蓄释热全过程综合分析如图7～10 所示。由图7 可知，三种模型的液相率在短时间内急剧升高，Case 1、Case 2、Case 3 的完全熔化时间依次为470、250、225 s，Case 3 所需时间最短，Case 1所需时间最长。三种模型释热过程所需时间较长，释热时间30 min，液相率依次为52.49%、10.10%、10.30%；释热时间50 min，液相率依次为37.43%、0%、0.71%。可见，Case 2 最先达到完全凝固，完全凝固时间为2918 s；其次是Case 3，完全凝固时间为3443 s；Case 1 所需时间最长。如图8 所示，将石蜡的传热过程分为三个阶段：蓄热段、间歇段、释热段。在蓄热段Case 3中石蜡平均温度始终高于其他模型，在释热段石蜡的平均温度均出现短时间急剧下降，释热时间100 s，三个模型石蜡的平均温度由380.00 K 依次降为325.73、319.31、317.52 K；当石蜡平均温度达到凝固温度315.15 K，三个模型所需时间依次为254、169、145 s；达到凝固温度后，石蜡的平均温度与时间呈线性变化，Case 2、Case 3 几乎重合，与Case 1 相比温度变化更快。综合分析蓄释热全过程，通过添加次肋强化了传热，肋片梯度分布对熔化过程有利，对凝固过程没起到有利的作用。石蜡蓄释热过程具有熔化时间短、释热时间长的特点。一方面由于石蜡熔化过程伴随着热传导与对流换热的协同作用，释热过程对流换热微弱以热传导为主；另一方面由于石蜡的熔化温度315.15 K 更接近于300.00 K，距释热初温380.00 K较远。

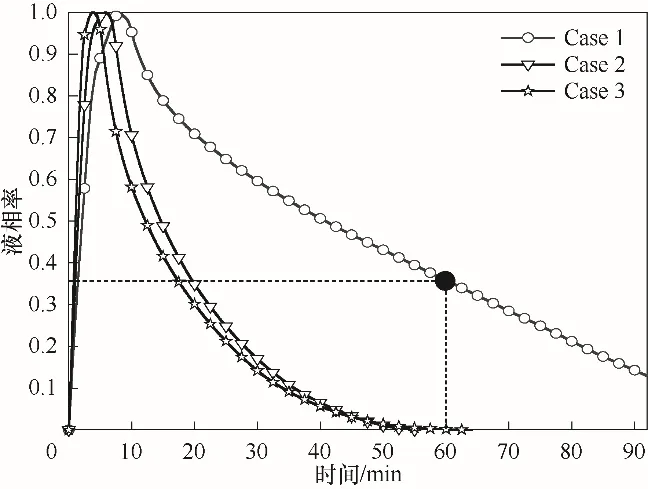
图7 三种模型蓄释热过程相变材料液相率变化Fig.7 Changes in the liquid fraction of phase change materials during heat storage and release process of three models

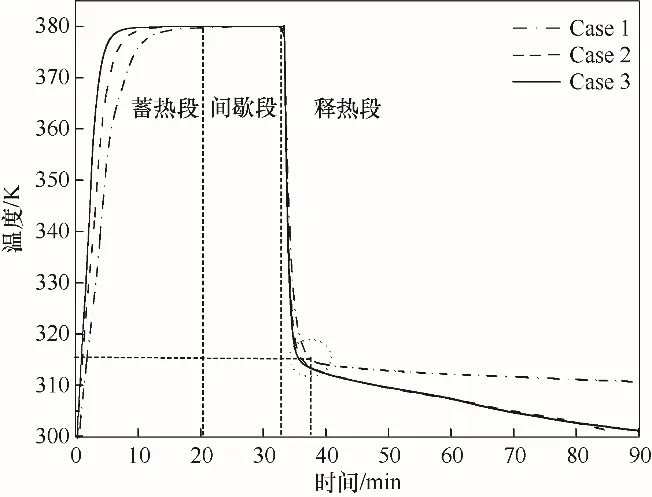
图8 三种模型蓄释热过程相变材料平均温度变化Fig.8 Changes in the average temperature of phase change materials during heat storage and release process of three models

三个模型Case 1、Case 2、Case 3 蓄释热过程石蜡平均速度瞬态变化如图9 所示，蓄热过程的速度变化呈先增大后减小的趋势，初期和后期速度随时间均呈线性变化，中期速度保持在一定范围内波动并出现最大速度依次为：4.743、2.693、6.281 mm∕s，可见肋片的梯度分布有利于液体石蜡的扰动。释热过程初期，液体石蜡突然受到管内温度为300.00 K 的流体冷却，在开始的5 s内具有释热的最大速度依次为：11.069、4.389、8.254 mm∕s，这是由于液体石蜡突然受到边界上的热扰动产生的流动，而后速度下降直到释热约7 min 降低为零。综合分析，石蜡的流动引起的自然对流换热对蓄热过程中期及释热过程初期起到重要的作用。如图10所示，蓄释热过程热通量均随时间减小最终趋于零，这是由于非稳态传热石蜡与壁面的传热温差逐渐减小，导致传热速度降低，当温差为零时，蓄释热结束，无热量传递。对比分析，Case3 的蓄释热热通量最大。因此，梯度树状肋储热系统传热性能最优。

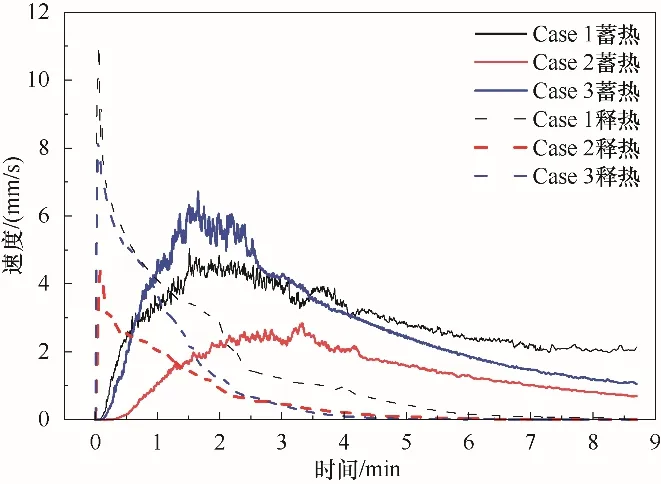
图9 三种模型蓄释热过程相变材料速度变化Fig.9 Changes in the velocity of phase change materials during heat storage and release process of three models

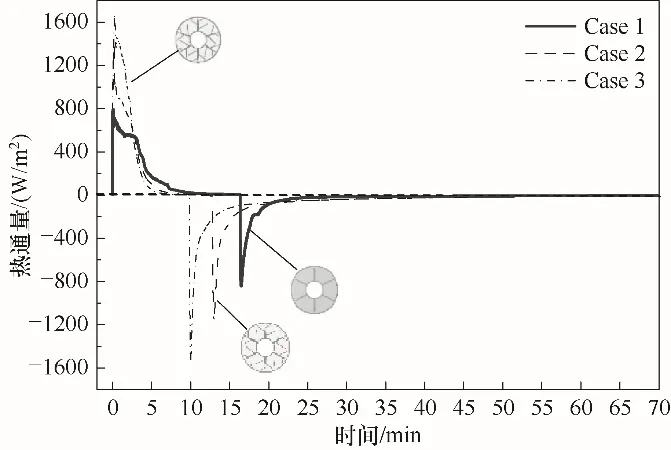
图10 三种模型蓄释热过程热通量变化Fig.10 Changes in the heat flux density during heat storage and release process of three models

3.3 场协同理论分析蓄释热传热特性

如图11、图12所示，石蜡熔化过程中，Case 1 的场协同数基本稳定在0.02，且不随时间发生较大的变化；Case 2 和Case 3 的场协同数随蓄热时间呈线性下降的趋势，二者的场协同数大小相差不大；在时间τ＜150 s时，Case 2和Case 3的场协同数均大于Case 1，在50 s 时，Case 1、Case 2 和Case 3 的场协同数依次为：0.01964、0.05729、0.04869，而后Case 1 的场协同数略大于Case 2 和Case 3。石蜡的凝固过程中，Case 1 的场协同数变化不大，稳定在0.1 左右，Case 2 和Case 3 的场协同数随释热的进行略有升高且均高于Case 1。这是由于与六纵肋片相比采用雪花型肋片和梯度树状肋片使空间温度分布更均匀，影响到速度场的空间分布，从而加强了动量传递过程。说明在主肋上通过增设次肋可以提高流体速度场和温度场的协同程度。

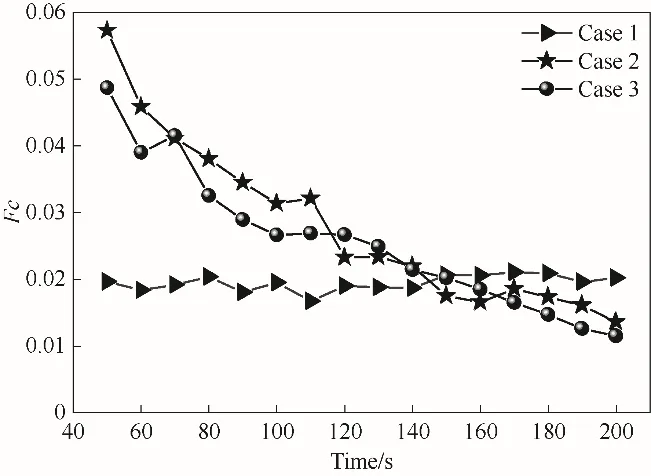
图11 三种模型熔化过程石蜡场协同数Fc的瞬态变化Fig.11 Transient changes in synergy number Fc of paraffin field in melting process of three models

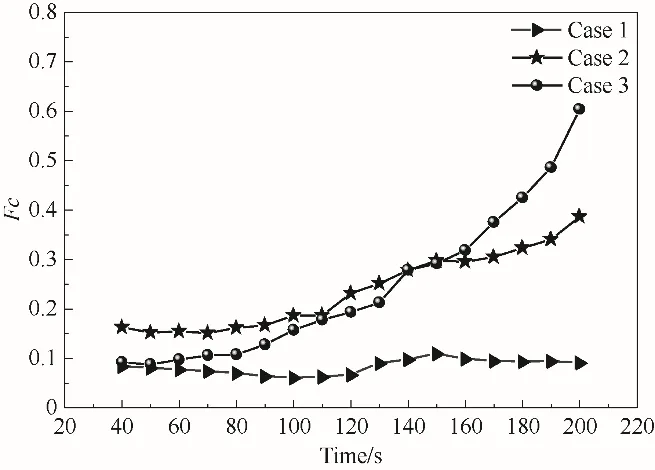
图12 三种模型释热过程石蜡场协同数Fc的瞬态变化Fig.12 Transient changes in synergy number Fc of paraffin field during heat release of three models

3.4 相变材料熔化温度对储释热传热特性的影响

考虑到相变储热系统相变材料的蓄释热时间，以梯度树状肋储热系统（Case 3）为模型分析石蜡熔化温度对蓄释热时间的影响。如图13所示，以石蜡RT35、RT44、RT82 熔 点 温 度 依 次 分 别 为315.00、340.00、360.00 K 进行分析[35-36]，相应的完全熔化时间为224、374、703 s；完全凝固时间为3439、1089、842 s。可见随着石蜡熔化温度的升高，完全熔化时间增长，完全凝固时间缩短。由图14、图15可知，蓄热段低熔化温度的石蜡温升最快；释热过程开始，石蜡由初温380.00 K 快速降低到达熔化温度，而后需要较长的时间进行释热。释热过程初始阶段石蜡热通量较大，三个熔化温度的最大热通量依次为1662、1051、876 W∕m2，而后热通量降低，最后趋于零释热结束，释热量随熔化温度的升高而减小。可见，热通量越大温度梯度越大，温度曲线斜率越陡峭，熔化温度为315.00、340.00 K 的石蜡先释热结束，热通量的变化直接影响释热过程传递的热量，在热通量较大时释热速度较大，焓曲线先增加而后趋于平缓，且随熔点温度的升高而减小。因此，在选择相变材料时要综合考虑熔化温度、蓄释热初温和终温及储热量的要求。

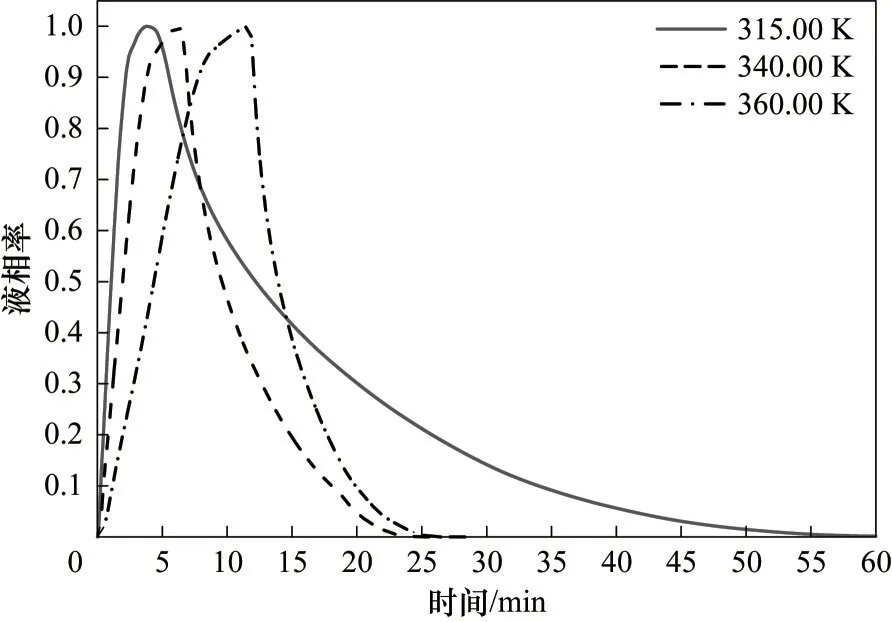
图13 不同熔化温度蓄释热过程石蜡液相率变化Fig.13 Changes in the liquid fraction of paraffin during heat storage and release at different melting temperatures

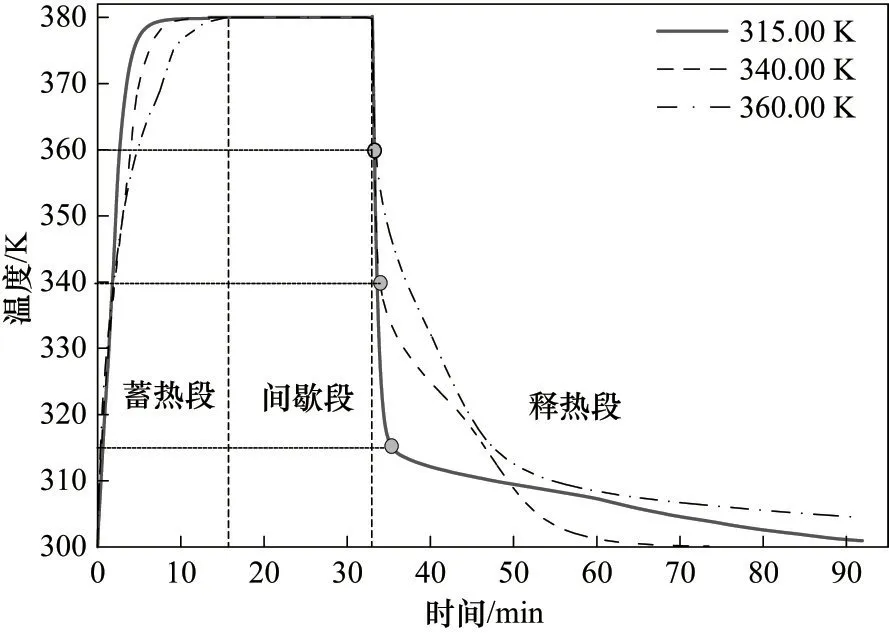
图14 不同熔化温度蓄释热过程石蜡平均温度变化Fig.14 Changes in the average temperature of paraffin during heat storage and release at different melting temperatures

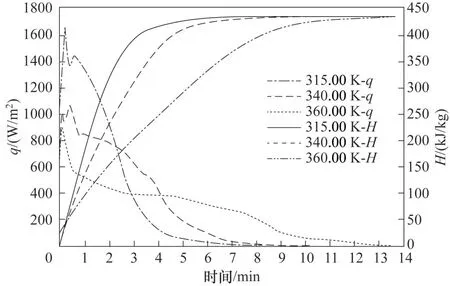
图15 不同熔化温度释热过程石蜡释热量变化Fig.15 Changes in the heat release capacity of paraffin at different melting temperatures

4 结 论

本文利用Fluent软件对相变储热系统传热特性进行模拟，针对相变材料的熔化和凝固过程的传热机理进行综合分析，对相变材料熔化温度对蓄放热时间的影响进行了研究，结合场协同理论对相变储热系统的温度场和速度场的协同特性进行分析，得出以下结论。

（1）针对三种相变储热模型的蓄释热过程进行综合分析。通过相变材料的液相率、平均温度、平均速度及热通量结合云图分析蓄释热过程传热机理，石蜡熔化过程伴随着热传导与自然对流的协同作用，凝固过程对流换热微弱以热传导为主。综合分析梯度树状肋储热系统传热性能最优。

（2）从场协同的角度分析了三种模型蓄释热传热特性，与六纵肋片相比，采用雪花型肋和梯度树状肋使空间温度分布更均匀，影响到速度场的空间分布，从而加强了动量传递过程。说明在主肋上通过增设次肋可以提高流体速度场和温度场的协同程度。

（3）相变材料的熔化温度影响着蓄释热时间。石蜡熔化温度分别为315.00、340.00、360.00 K，完全熔化时间依次为224、374、703 s；完全凝固时间依次为3439、1089、842 s。可见，随着石蜡熔化温度的升高，完全熔化时间增长，完全凝固时间缩短。释热过程开始，石蜡由初温快速降到熔化温度，而后需要较长的时间进行释热。熔化温度为360.00 K的石蜡释热最慢，因此，在选择相变材料时要考虑熔化温度、蓄释热初温和终温及储热量的要求。