改进匈牙利法的多层反导协同作战目标分配模型*
季军亮,李龙跃,杨小雷,张微
(空军工程大学 防空反导学院,陕西 西安 710051)
0 引言
多层反导协同作战目标分配,是将来袭弹道导弹指派给多层反导体系所属作战单元的活动,解决的是来袭弹道目标由“谁”拦截的问题,是多层反导协同作战的关键环节。多层反导协同作战目标分配模型作为反导指挥信息系统的底层支撑,是目标分配准则的抽象再现和数学表达,模型构建合理与否,将直接影响反导作战效能[1]。肖金科等[2]分析了区域反导目标分配流程与准则,构建综合拦截概率和作战效费比的目标分配模型,并给出了该目标分配模型转化为基本0-1 规划问题的方法,针对该多约束目标分配优化模型对高寻优、强实时求解算法的需求,引入改进的克隆选择、云自适应变异等算子,提出快速收敛的克隆选择算法;刘韬等[3]针对反导拦截过程中反导武器与来袭目标的分配问题,建立武器目标分配数学模型,引入遗传算法,并提出一种算法改进方案来求解分配问题;徐浩等[4]采用三角模糊数,刻画不确定的目标威胁度,基于模糊多目标规划建立了火力分配模型,提出了用于求解模型的多目标量子行为粒子群算法,并通过实例仿真验证了模型的合理性和算法的有效性。
以上学者从多个视角对反导目标分配问题进行了探索,在多层反导目标分配模型构建方面取得了一定成果,但由于相关研究围绕“来袭导弹-反导武器-保卫目标”一体化考虑的不够充分,指标体系构建不够完善,算法设计过于复杂,致使所建立的目标分配模型在多层反导协同作战中的适用性、实用性不够强。多层反导协同作战目标分配,输出的是来袭弹道导弹与反导作战单元的配对序列,是优选“来袭弹道目标-反导作战单元”的过程。因此,多层反导协同作战目标分配模型的构建,必须将来袭弹道导弹、反导作战单元和地面保卫目标综合考虑,并着重分析来袭弹道导弹威胁度和反导作战单元拦截有利度2 个配对实体的基本属性,同时,要基于配对实体的属性分析,结合多层反导协同作战及其目标分配的特点,选择适用的优化算法。
1 弹道导弹威胁度评估模型
弹道导弹威胁度评估,是对攻击地面保卫目标的弹道导弹,威胁度大小的分析和评判。影响弹道导弹威胁度的因素有很多,归纳起来主要包括被攻击目标重要程度、被攻击目标抗毁能力、弹头落地剩余时间、弹头破坏威力、弹道导弹在反导发射区内飞行时间等5 类指标,为便于在后续计算中统一使用5 类指标参量,这里将各指标参量均转换为越大越好型。
1.1 被攻击目标重要程度
弹道导弹进袭的最终目的是有效毁伤地面保卫目标,根据弹道导弹可能的落点位置即可明确被攻击目标的位置范围。根据地面保卫目标的地位作用,其重要程度大致可划分为3 个等级:一级、二级和三级,攻击不同重要程度地面目标的弹道导弹,其威胁度自然也不一样[5]。一、二、三级地面保卫目标分别用数字1、2、3 表示其重要程度,鉴于被攻击目标重要程度对威胁评估的高水平影响,这里采用重要程度表征数字n1k与3 相比的方式进行归一化处理,则第j 枚弹道导弹所攻击的第k 个地面保卫目标重要程度指标的表达式为

对于弹道导弹威胁度而言,Zjk为越大越好型参量,无需进行第二次归一化处理。根据式(1)可知,一、二、三级地面保卫目标的重要程度分别为1、2/3、1/3。
1.2 被攻击目标抗毁能力
地面保卫目标抗毁能力表征了其在没有外部防护措施的情况下,遭弹道导弹攻击后,能够保持基本运行能力的能力。地面保卫目标的抗毁能力越强,弹道导弹对该目标实施打击的效果就越差,也由此决定了来袭弹道导弹威胁度的降低。根据文献[6]的定义,将地面保卫目标抗毁能力划分为极强、强、较强、弱、很弱共5 个等级,5 个等级抗毁能力水平下,地面保卫目标在遭受预期规模的弹道导弹攻击时,所对应的毁伤程度为未毁伤、轻微毁伤、中度毁伤、严重毁伤、摧毁。其中,未毁伤、轻微毁伤和中度毁伤等级时地面保卫目标能够保持基本运行能力。从高到低5 个等级抗毁伤能力分别用数字 5,4,3,2,1 表示,这里采用抗毁伤能力表征数字m2k与1~5 之和相比的方式进行第一次归一化处理,可得:

由式(2)可知,地面保卫目标抗毁能力越强,对应的来袭弹道导弹威胁度就越低,为将指标转换为越大越好型参量,需进行第二次归一化处理,即用1减去式(2),则第j 枚弹道导弹所攻击的第k 个地面保卫目标抗毁能力指标Kjk的表达式为

根据式(3)可知,地面保卫目标5 个等级抗毁伤能力分别为 10/15、11/15、12/15、13/15、14/15。
1.3 弹头落地剩余时间
弹道导弹飞行速度快,从发射到弹头落地的全弹道飞行时间短,近程弹道导弹的飞行时间仅几分钟,中程弹道导弹的飞行时间也就十几分钟[1,8]。弹道导弹进攻作战时,其弹头落地剩余时间越短,对地面保卫目标进行的打击越早,地面反导力量的作战准备时间就越紧迫,与之相对应,该弹道目标的威胁程度也就越高。需要强调的是,弹头落地剩余时间的计算时间起点是统一的,均以多层反导体系跟踪制导系统在同一攻击波次内首次捕获来袭弹道目标的时刻为准[1,7]。设同一攻击波次内共有ng枚弹道导弹,其中第j 枚弹道导弹的弹头落地剩余时间为tsj,这里采用tsj与所有弹头落地剩余时间之和相比的方式,进行第一次归一化处理,可得:

由式(4)可知,弹头落地剩余时间越长,对应的来袭弹道导弹威胁度就越低,为将指标转换为越大越好型参量,需进行第二次归一化处理,即用1 减去式(4),则被攻击目标抗毁能力指标Tsj的表达式为

1.4 弹头破坏威力
弹头破坏威力用TNT 当量表示,TNT 当量越大,其对地面保卫目标的破坏威力就越强。设同一攻击波次内可能来袭弹道导弹所携带弹头的最大TNT当量为 dmax,第 j 枚弹道导弹弹头的 TNT 当量为 dj,鉴于弹道导弹威胁度对弹头威力的敏感性,这里采用第j 枚弹道导弹弹头的TNT 当量与最大TNT 当量相比的方式进行第一次归一化处理,则有第j 枚弹道导弹弹头的破坏威力指标可表征为

对于弹道导弹威胁度而言,Dj为越大越好型参量无需进行第二次归一化处理。
1.5 弹道导弹在反导发射区内飞行时间
弹道导弹在反导发射区内飞行时,反导作战单元即可对该弹道目标发射拦截弹,且拦截弹可以一定概率在反导杀伤区内对弹道目标进行毁伤[1,7]。由此可知,弹道目标在多层反导体系所属反导作战单元的发射区内飞行时间越长,反导作战单元对来袭弹道目标的射击次数就越多,成功毁伤概率也就越大,与之相对应,来袭弹道导弹所产生的威胁就越小,反之,其威胁度就越大。需要强调的是,这里的发射区内飞行时间,是第j 枚弹道导弹在多层反导体系中所有反导作战单元发射区内飞行时间的总和,即:

式中:tffj为第j 枚弹道导弹在多层反导体系中所有反导作战单元发射区内的飞行时间总和;tffji为第j 枚弹道导弹在第i 个反导作战单元发射区内的飞行时间;m 为多层反导体系所属反导作战单元的数量。这里采用第j 枚弹道导弹在多层反导体系中所有反导作战单元发射区内的飞行时间总和tffj,与所有来袭弹道导弹在多层反导体系中所有反导作战单元发射区内的飞行时间总和相比的方式,进行第一次归一化处理,则有:

由式(8)可知,弹道导弹在反导作战单元发射区内飞行时间越长,对应的来袭弹道导弹威胁度就越低,为将指标转换为越大越好型参量,需进行第二次归一化处理,即用1 减去式(8),则弹道导弹在反导发射区内飞行时间指标的表达式为

需要说明的是,弹道导弹威胁度评估的以上5类指标,部分为已知参量,部分可通过仿真条件下模拟推演获得。
1.6 弹道导弹威胁评估模型构建
鉴于以上5 类指标对来袭弹道导弹威胁度的影响水平有所差异,因此,需对各指标参量赋予一定的权重。指标权重赋值采用专家打分法确定,具体步骤为:选择在反导实兵研练、反导仿真推演、弹道导弹作战运用等方面,具有丰富经验的部队指挥员和科研院所技术人员若干名(奇数)作为专家;每名专家针对每项指标对弹道导弹威胁度的影响水平打分(10 分制),而后求取各项指标的专家打分平均指标的权重进行归一化处理,可得第jwxzb项指标的最终权重为

以上5 类指标对于来袭弹道导弹威胁评估而言,均为越大越好型参量,由此可得第j 枚来袭弹道导弹威胁度Wjk的计算模型为
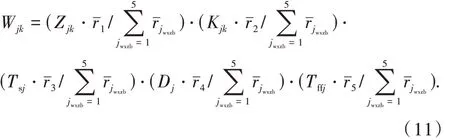
2 反导作战单元拦截有利度分析模型
反导作战单元拦截有利度,是衡量反导作战单元对来袭弹道导弹拦截作战条件好坏程度的参量。通常情况下,反导作战单元对来袭弹道导弹拦截有利度越高,越适宜对该弹道导弹进行拦截。影响反导作战单元拦截有利度的因素,主要包括反导作战单元对来袭弹道导弹的单发毁伤概率、来袭弹道导弹在反导作战单元发射区内的飞行时间、反导作战单元可用拦截弹数量以及反导作战单元单发拦截弹费用等4 类指标。为便于在后续计算中统一使用4 类指标参量,这里将各指标参量转换为越大越好型。
2.1 反导作战单元对来袭弹道导弹的单发毁伤概率
反导作战单元对来袭弹道导弹的单发毁伤概率,是衡量反导作战单元对来袭弹道导弹拦截作战能力的重要指标,也是评判该反导作战单元拦截有利度的主要参量。对来袭弹道导弹的单发毁伤概率越高,反导作战单元的拦截作战能力就越强,其对来袭弹道导弹的拦截有利度就越高。设第i 个反导作战单元对第j 枚弹道导弹的单发毁伤概率为pij,则根据以上分析,pij对于反导作战单元拦截有利度而言是越大越好型指标参量[7-9]。鉴于pij本身为概率型参量即0 ≤pij≤1,这里不再对其进行归一化处理。需要说明的是,单发拦截弹反导毁伤概率不是固定值,而是与来袭弹道导弹目标特性相关的变量,鉴于反导作战单元较高的制导精度,该变量数值的确定方法,可参照文献[7]中关于单发杀伤概率确定方法的“第2 种情况”进行。
2.2 来袭弹道导弹在反导作战单元发射区内的飞行时间
相对而言,来袭弹道导弹在反导作战单元发射区内的飞行时间越长,反导作战单元对弹道目标的允许射击次数就越多。根据文献[7]分析结果可知,在反导作战单元单发毁伤概率一定的情况下,增大反导拦截弹发射数量是提高对来袭弹道导弹毁伤概率的重要途径之一。设第j 枚来袭弹道导弹在第i 个反导作战单元发射区内的飞行时间为tffji,其在多层反导体系所有反导作战单元的发射区内飞行时间总和为tffj,则有

采用第j 枚来袭弹道导弹在第i 个反导作战单元的发射区内飞行时间,与该弹道导弹在多层反导体系所有反导作战单元的发射区内飞行时间总和相比的方式,进行第一次归一化处理,则有

对于反导作战单元拦截有利度而言,来袭弹道导弹在反导作战单元发射区内的飞行时间指标Tffji为越大越好型参量,无需进行二次归一化处理。
2.3 反导作战单元可用拦截弹数量
反导作战单元可用拦截弹数量通常指的是,在不进行拦截弹装填的情况下,反导作战单元可以使用的拦截弹数量,即反导作战单元发射装置满载时的拦截弹总数。设第i 个反导作战单元可用拦截弹数量为nlji,则多层反导体系可用反导拦截弹数量nlj为

采用第i 个反导作战单元可用拦截弹数量与多层反导体系可用反导拦截弹总数相比的方式,进行第一次归一化处理,则有

对于反导作战单元拦截有利度而言,反导作战单元可用拦截弹数量为越大越好型参量,无需进行二次归一化处理。
2.4 反导作战单元单发拦截弹费用
反导作战单元单发拦截弹费用是指,发射一枚反导拦截弹所花费的成本。一般情况下,该成本以单发拦截弹本身的价值为主要构成。设第i 个反导作战单元单发拦截弹费用为e1i,则多层反导体系所属反导作战单元的单发拦截弹费用总和e1为

用第i 个反导作战单元单发拦截弹费用,与多层反导体系所属反导作战单元的单发拦截弹费用总和相比,进行第一次归一化处理,则有

对于反导作战单元拦截有利度而言,E'1i为越小越好型参量,为将指标转换为越大越好型参量,需进行第二次归一化处理,即用1 减去式(17),则反导作战单元单发拦截弹费用指标E1i的表达式为

同样,反导作战单元拦截有利度分析的以上4类指标,绝大部分为已知参量,个别参量可通过仿真条件下的模拟推演获得。
2.5 反导作战单元拦截有利度模型构建
鉴于以上4 类指标对反导作战单元拦截有利度的影响水平有所差异,因此,需对各指标参量赋予一定的权重。与弹道导弹威胁度评估指标一样,反导作战单元拦截有利度指标权重赋值也采用专家打分法确定,具体步骤为:选择在反导实兵研练、反导仿真推演等方面,具有丰富经验的部队指挥员和科研院所技术人员若干名(奇数)作为专家;每名专家针对每项指标对反导作战单元拦截有利度的影响水平打分(10 分制),而后求取各项指标的专家打分 平 均 值 rˉiylzb;用 第 iylzb项 指 标 的 专 家 打 分 平 均 值 rˉiylzbiylzb项指标的权重进行归一化处理,可得第iylzb项指标的最终权重为

以上4 类指标对于反导作战单元拦截有利度而言,均为越大越好型参量,由此可得,第i 个反导作战单元对第j 枚来袭弹道导弹的拦截有利度计算模型为
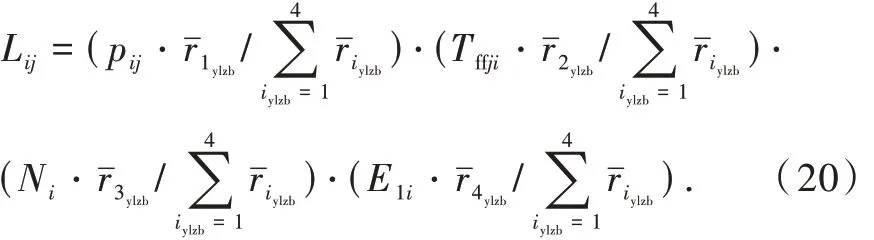
3 基于改进匈牙利法的多层反导协同作战目标分配模型
多层反导协同作战目标分配的实质是“任务指派”,它是一种特殊的整数规划问题,是给不同反导作战单元分派拦截任务的过程,最终目的是求取多层反导协同作战目标分配的最优方案。对于多层反导协同作战目标分配规划而言,选择合适的算法极为重要,该算法应满足以下要求:一是原理简单、便于计算。反导作战时效性极强、战机稍纵即逝,无论临战任务规划还是战时任务规划,都必须满足输入信息更新后、指挥控制系统执行前的时间限制,如此,就对多层反导协同作战目标分配的时效性提出了极高要求。为满足这一要求,目标分配求解算法也就必须具有简单快捷的基本特征。二是优势突出、解算有效。所选算法必须具有针对任务指派问题的内在逻辑,能够有效解决指派问题,并且对于多层反导协同作战目标分配的复杂性,经适应性改进后具有较好的适应能力。
匈牙利法(Hungarian algorithm)是为解决指派性问题而专门设计的算法,该方法架构简单、运算快捷,与遗传算法、神经网络等启发式算法相比,能从底层设计上直接避免局部寻优、运算资源投入过大等问题的出现,完全满足上述要求,因此,本文运用匈牙利法对多层反导协同作战目标分配进行优化[10-13]。
3.1 多层反导协同作战目标分配规划建模
根据匈牙利法解决分配问题的基本原理[10,12],结合多层反导协同作战运行机制与实施流程,构建基于匈牙利法的多层反导协同作战目标分配模型。
3.1.1 界定有关概念
(1)分配元
多层反导体系中的一个反导作战单元,与其所拦截的一枚来袭弹道导弹构成的配对组合称为分配元,用Uij表示。由于反导作战单元尤其是中段和末段高层反导作战单元,大多具有多目标拦截能力,因此,一个反导作战单元在一次目标分配中可形成多个分配元[14]。
(2)综合效率指标
确定一个综合考虑来袭弹道导弹威胁度及反导作战单元拦截有利度的综合效率指标,即

式 中 :aij为 分 配 元 Uij的 综 合 效 率 指 标 ;Wjk为 第 j 枚来袭弹道导弹的威胁度;Lij为第i 个反导作战单元对第j 枚来袭弹道导弹的拦截有利度。
(3)反导作战单元转火系数
同一攻击波次内的来袭弹道导弹,到达多层反导体系火力范围的时间(到火时间)不完全相同,反导作战单元对来袭弹道导弹进行射击也未必百分百成功摧毁,为了保证多层反导体系对空火力的持续性和有效性,就必须考虑体系内反导作战单元转移火力的因素。反导作战单元转移火力,须满足射击周期不大于目标批次间隔这一基本条件。用cij表示作战单元的转火系数,即对

(4)目标通道空闲系数
用来表示某一时刻反导作战单元的目标通道状态,有空闲目标通道或没有空闲目标通道,在有空闲目标通道的前提下,方可对来袭弹道导弹实施拦截。以Fij表示第i 个反导作战单元的目标通道空闲系数,则

(5)弹道导弹毁伤系数
表征反导作战单元对分配元内来袭弹道目标的杀伤效果—摧毁或未摧毁,若来袭弹道导弹未被摧毁,则需要进行二次目标分配,由同火力层次或不同火力层次的其他反导作战单元再次实施拦截。用hij表示第i 个反导作战单元对第j 个来袭弹道目标的毁伤系数,则有

在具体仿真计算中,可设定当第j 枚弹道导弹被服务的毁伤概率达到指定数值PZD时,认为弹道目标被摧毁即,hij= 0;否则认为弹道目标未被摧毁,即hij= 1。PZD值的计算通常有2 种确定方法:①若上级指定对第j 枚弹道导弹的杀伤概率,则依据上级给定概率确定;②若上级未指定对j 枚弹道导弹的杀伤概率,则依据文献[7]中反导拦截弹杀伤概率增长率和弹药相对消耗量的方法综合确定。
3.1.2 多层反导协同作战目标分配模型
根据以上分析,可得多层反导协同作战目标分配模型为

式中:m 为多层反导体系所属反导作战单元的数量;ng为同一攻击波次内来袭弹道导弹的数量;Wjk为同一攻击波次内第j 枚来袭弹道导弹的威胁度;Lij为第i 个反导作战单元对第j 枚来袭目标的拦截有利度。
为将目标分配模型转换为基于匈牙利法的标准表达式,现对式(25)内的效率矩阵元素进行转换,具体方法如下:

式中:bij为转换后的新效率矩阵元素;C 为max(WjkLij),则转换后的多层反导协同作战目标分配模型为
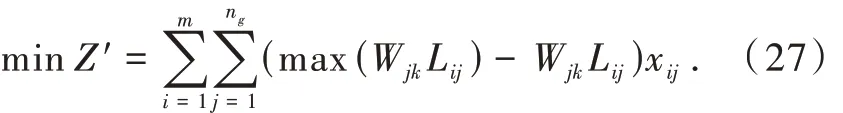
3.1.3 基于改进匈牙利法的多层反导协同作战目标分配解算步骤
Step 1:根据多层反导协同作战任务规划构设的作战想定,明确反导作战单元、来袭弹道导弹及地面保卫目标的相关参数指标,并计算来袭弹道导弹威胁度Wjk及反导作战单元拦截有利度Lij。
Step 2:计算各分配元的综合效率指标WjkLij,并以各分配元的综合效率指标为元素构建效率矩阵[WjkLij],此时该效率矩阵为极大值型,采用式(26)的方法对效率矩阵进行变换得[max(WjkLij) - WjkLij],将目标函数由求极大值问题变为求极小值问题。对于多通道反导作战单元,只需模拟增加多通道反导作战单元数量即可,由此形成的分配元综合效率指标均相同。
Step 3:参照文献[10]“匈牙利法的基本原理”中的方法求解变换后的矩阵,进而得到第一次目标分配优化方案。
Step 4:在前一次目标分配优化的基础上,综合考虑弹道导弹毁伤系数、目标通道空闲系数和反导作战单元转火系数,形成二次目标分配效率矩阵,并按照step 2、step 3 的方法进行求解,得到二次目标分配优化方案。
Step 5:重复step 3、step 4 直到效率矩阵全部为“0”,即所有目标(含未被摧毁目标)均被分配至反导作战单元。
Step 6:综合多次目标分配结果,即得到多层反导体系对一波次来袭弹道导弹的最终目标分配方案。
由以上分析可知,本文对匈牙利法的改进主要体现在应用方式上,传统匈牙利法解决目标分配问题往往是一次分配,得到优化分配方案即可,而这种模式显然无法满足多层反导协同作战火力运用的实际需求。因此,论文引入了反导作战单元转火系数、目标通道空闲系数和弹道导弹毁伤系数3 个影响因子,并通过匈牙利法的反复运用以及目标分配优化方案的不断迭代,最终形成多层反导协同作战目标分配方案。
4 仿真验证
以红蓝双方弹道导弹攻防作战为背景,开展多层反导协同作战案例仿真,以对基于改进匈牙利法的多层反导协同作战目标分配模型进行验证。
4.1 背景想定
红方保卫目标为红方所属核心要害目标区,其反导作战可用装备包括Z 型中段反导作战单元、G型末段高层反导作战单元和D 型末段低层反导作战单元,且限定中段、末段高层和末段低层反导火力层次,对1 枚来袭弹道导弹发射拦截弹数量分别不大于2 枚、4 枚、4 枚。红方保卫目标组成及分布情况如图1 所示。
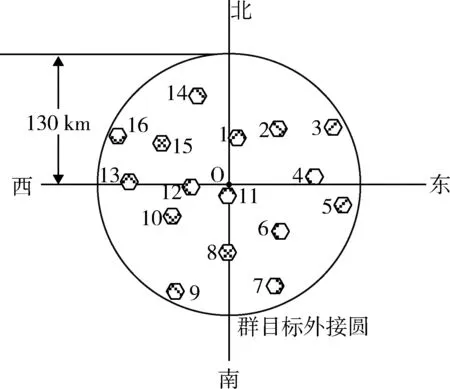
图1 红方保卫目标组成及分布情况Fig.1 Composition and distribution of red side security target
根据红方统帅部要求,多层反导体系对来袭弹道导弹的毁伤概率不得低于0.7,并明确要求对攻击第 1、3、5、8、11、15 号点状目标的来袭弹道导弹拦截毁伤概率不得低于0.9。
蓝方对红方保卫目标实施打击的弹型为陆射B型和潜射C 型弹道导弹,两型弹道导弹技战术参数如表1 所示。

表1 蓝方弹道导弹技战术参数Table 1 Technical and tactical parameters of blue side ballistic missile
根据蓝方弹道导弹技战术性能,设定弹道导弹攻击红方保卫目标的具体方案如表2 所示。

表2 蓝方弹道导弹攻击红方保卫目标的方案Table 2 Scheme of blue ballistic missile attacking red side defense target
红方三型反导作战单元对蓝方弹道导弹作战能力如表3 所示。

表3 红方反导作战单元对蓝方弹道导弹作战能力Table 3 Combat capability of red anti missile combat unit against blue ballistic missile
4.2 仿真计算
以多层反导体系所能拦截的弹道导弹数学期望表征反导作战效能,考虑作战费用最小、目标最低毁伤概率、拦截弹发射数量和可用拦截弹数量等约束条件,即

采用LINGO(交互式的线性和通用优化求解器)软件对设置实例进行求解。LINGO 软件可用于求解非线性规划,也可用于解决线性和非线性方程组。软件内置建模语言,允许决策变量是整数,操作使用方便灵活,而且执行速度非常快,便于和EXCEL、数据库等其他软件交换数据。仿真实验在硬件配置为CPU 主频2.6 GHz、内存容量为32 GB的计算机下进行,共耗时26 s。经过计算,得到多层反导作战目标分配方案,取其中一套方案如表4所示。
采用常规数学解析法对表4 目标分配方案进行验证,该方案完全满足红方保卫目标反导作战要求,充分说明了基于改进匈牙利法的多层反导协同作战目标分配模型的合理性与有效性。

表4 多层反导协同作战目标分配方案Table 4 Target allocation scheme of multi-layer antimissile cooperative operation
5 结束语
本文从反导作战目标分配的输入变量和输出结果着眼,分别构建了弹道导弹威胁度评估模型和反导作战单元拦截有利度分析模型,同时,结合多层反导作战及其目标分配的特点,对匈牙利法进行了适应性改进,并基于特定的反导作战场景,采用成熟的计算软件,对文章所构建模型进行了仿真验证,充分说明了模型的有效性与合理性。文中目标分配模型构建不仅强调了多层反导体系总体作战效能,也兼顾了拦截作战费效比,充分体现了多层反导火力“协同”作战的优越性,研究成果对反导作战理论研究及多层反导协同作战实践均具有一定的参考价值。

