考虑执行器性能约束的高速列车容错跟踪控制

徐传芳，谷晓琳，王龙达

（1.大连交通大学 自动化与电气工程学院，大连 116028；2.大连交通大学 计算机与通信工程学院，大连 116028）

随着计算机、通信、网络以及控制技术的发展，列车自动驾驶运行模式取代人工驾驶模式已经成为必然趋势[1]。实现对期望轨迹曲线的可靠精确跟踪是列车实现自动驾驶需要解决的核心问题和必要条件[2]。受列车运行速度和运行跨度的增加以及时变的运行阻力、不确定的外部环境、不可避免的执行器饱和约束、不可预测的执行器故障等因素的影响，列车运行过程具有强非线性和不确定性。复杂且存在诸多执行器性能约束的高速列车非线性动力学系统，对列车自动驾驶跟踪期望轨迹曲线的控制算法提出了更高要求。考虑并抵御这些因素影响，满足高速列车对期望轨迹曲线跟踪的高精度和高可靠性要求，变得迫切且具有挑战性。

近年来，考虑诸多列车运行的影响因素，许多专家学者对高速列车的跟踪控制问题进行了探索与研究，并涌现出了大量的研究成果。文献[3]和文献[4]考虑基本阻力参数未知，分别基于自适应反步控制技术和自抗扰控制技术，设计了高速列车自动驾驶速度跟踪控制策略。进一步考虑附加阻力，文献[5]亦提出了高速列车自动驾驶系统的反步自适应跟踪控制策略，实现了列车在不同运行条件下的精确速度和位移跟踪。但是，上述文献仅考虑了列车基本阻力系数的未知性，并未考虑参数的时变性；而且上述控制器的设计均基于列车运行过程执行机构健康无故障的假设。然而执行器故障在所难免且可能导致列车跟踪性能下降，甚至系统不稳定。容错控制是系统在执行器故障时仍能保持较好性能的有效途径[6]。为此，很多学者提出了不同的列车容错跟踪控制策略[7-10]。文献[7]基于虚拟参数反步自适应控制方法，针对系统参数和基本阻力参数未知的高速列车，并考虑外界扰动、执行器故障、牵引/制动动态等，设计了高速列车的牵引/制动容错控制策略；文献[8]结合自适应技术和滑模控制方法，设计了高速列车的容错跟踪控制策略，有效地解决了执行器不确定且存在未知故障，列车部分参数未知且时变，附加阻力未知等因素对列车运行的影响。文献[9]考虑执行器故障，基本运行阻力和附加阻力的影响，分别针对参数时变界限未知，以及参数未知但有恒定已知上下限两种情况，结合自适应技术和具有时变系数的PID滑模面，研究了高速列车的跟踪控制问题。文献[10]提出了高速列车的分数阶有限时间速度跟踪控制算法，实现了考虑未知执行器故障、不确定气动阻力，以及外部阻力和车间力时，高速列车的快速高精度跟踪控制。

受牵引电机自身物理特性以及列车黏着防滑控制的需要等制约，执行器的输出存在饱和受限约束问题。然而，上述文献均未考虑执行器输出饱和问题，此问题的忽略必然会对列车跟踪控制系统的性能造成严重影响。为此，很多文献对执行器饱和约束下的列车跟踪控制问题进行了研究，并提出了相应的解决方案。文献[11]-[14]考虑执行器饱和引起的控制输入受限，通过引入辅助系统或设计鲁棒项，来补偿执行器饱和的影响，研究并设计了高速列车的速度跟踪控制器,它们均考虑了基本阻力参数以及附加阻力的影响。文献[13][14]同时还考虑了时变不确定性参数以及执行器故障的影响。

前述研究成果致力于解决面临列车质量、基本阻力和附加阻力难以确定，执行器存在饱和约束，以及执行器会出现不可预测故障等因素影响下的高速列车跟踪控制问题。但上述研究大多仅考虑了其中部分因素的影响，而且大部分文献并未考虑参数的时变性[3-5,7-12]，同时考虑执行器故障和执行器饱和问题的研究成果也还很不丰富[13,14]。另外，在现有关于高速列车跟踪控制策略的研究成果中，少有同时考虑执行器输出幅值和变化率饱和约束的文献。

综上，为了解决存在故障、输出幅值和变化率饱和等执行器性能约束，模型参数时变不确定，以及附加阻力干扰等影响下的高速列车速度跟踪控制问题，本文在文献[13]基础上，借鉴文献[15]处理执行器输出幅值和变化率约束的方法，基于双曲正切函数构造的辅助系统，构建了高速列车的增广速度跟踪控制系统模型，针对基于反步法的控制器存在复杂且计算量大的问题，选择动态面控制技术，并进一步结合自适应控制技术，设计了高速列车的鲁棒自适应动态面跟踪控制策略。基于Lyapunov稳定性理论证明了所设计高速列车容错跟踪控制系统的稳定性，并借助于数值仿真对控制器的性能进行了验证。

1 高速列车动力学增广系统模型

至此，式(1)(2)(4)(6)就构成了考虑故障、输出幅值和变化率等执行器性能约束的高速列车动力学增广系统模型。

控制目标：针对式(1)(2)(4)(6)构成的增广列车动力学模型系统，即针对存在执行器输出幅值和变化率饱和约束、执行器故障、模型参数时变不确定，以及附加阻力干扰等因素影响的高速列车，设计容错速度跟踪控制器，使得系统能够抵御上述因素的影响，在保持稳定的同时实现高速列车对期望速度曲线和位移曲线的精确跟踪。

2 容错跟踪控制器设计与稳定性分析

2.1 控制器设计

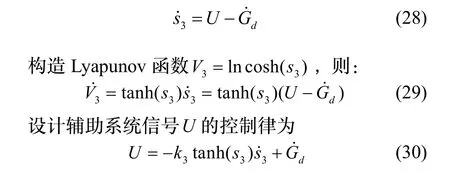
2.2 稳定性分析

2.1部分所描述的高速列车容错跟踪控制算法可以描述为定理1。

3 仿真验证

仿真模拟了列车在1400 s内的速度和位移跟踪情况。列车的期望速度曲线和期望位移曲线如图1所示。列车整个运行过程包括两个加速阶段、四个巡航阶段和三个减速阶段，运行最高时速为69.5 m/s（约250 km/h）。

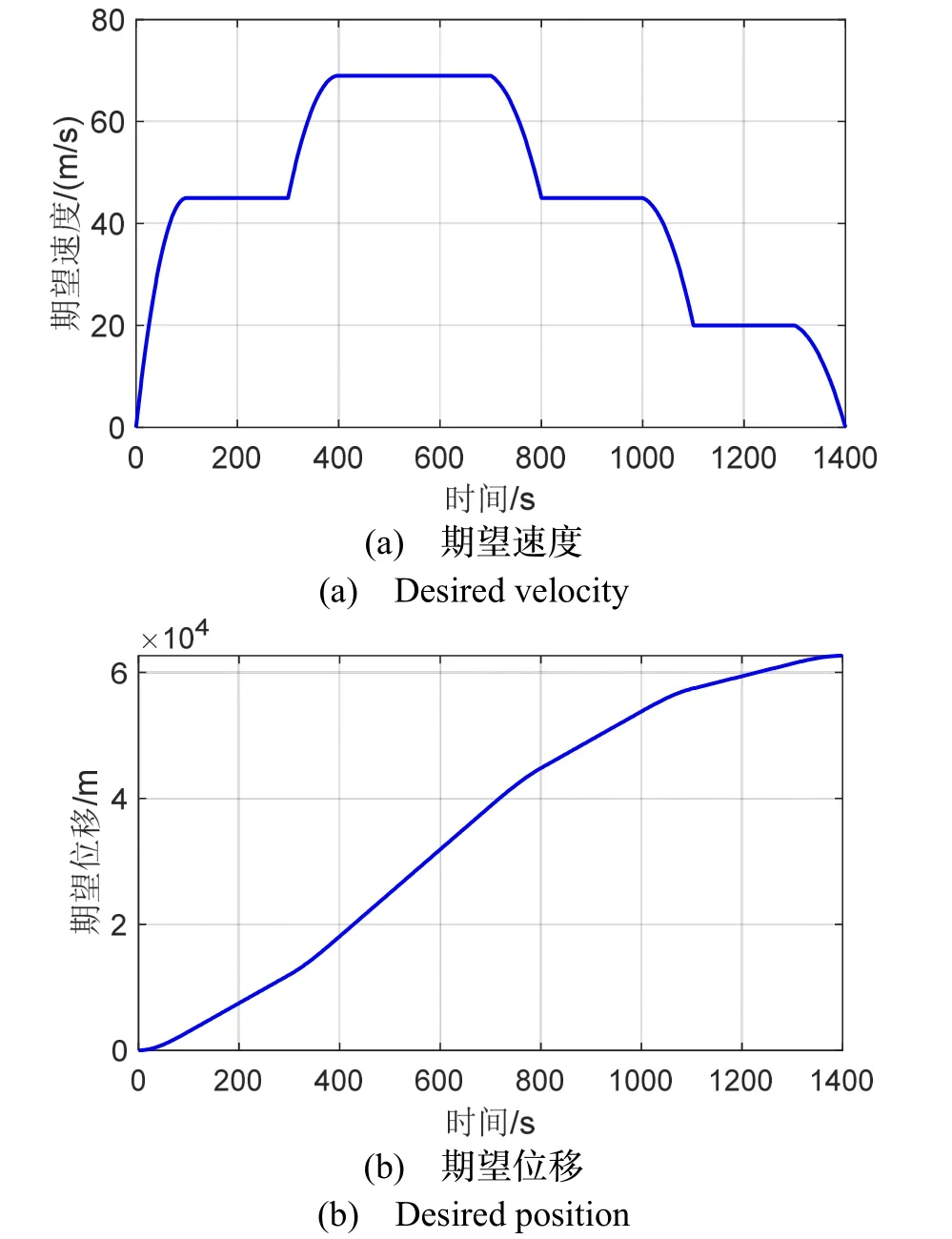
图1 列车期望速度和位移Fig.1 Desired velocity and position of train

仿真结果如图2-4所示。图2为列车实际速度和位移与它们的期望值之间的误差，可以看出列车工况切换、运行线路情况改变，以及列车执行器突然发生未知部分失效故障时，列车的暂态速度跟踪误差和位移跟踪误差分别在0.016 m/s和0.003 m范围内，速度和位移波动均很小；稳态时的速度跟踪误差和位移跟踪误差约为0.001 m/s和0.0005 m，具有较高的稳态跟踪精度。图3和图4分别为列车控制输入及其变化率的仿真结果，可以看出列车的控制输入无明显抖振，控制输入及其变化率均满足所设置饱和约束的要求。

图2 列车速度和位移跟踪误差Fig.2 Velocity and position tracking errors of train

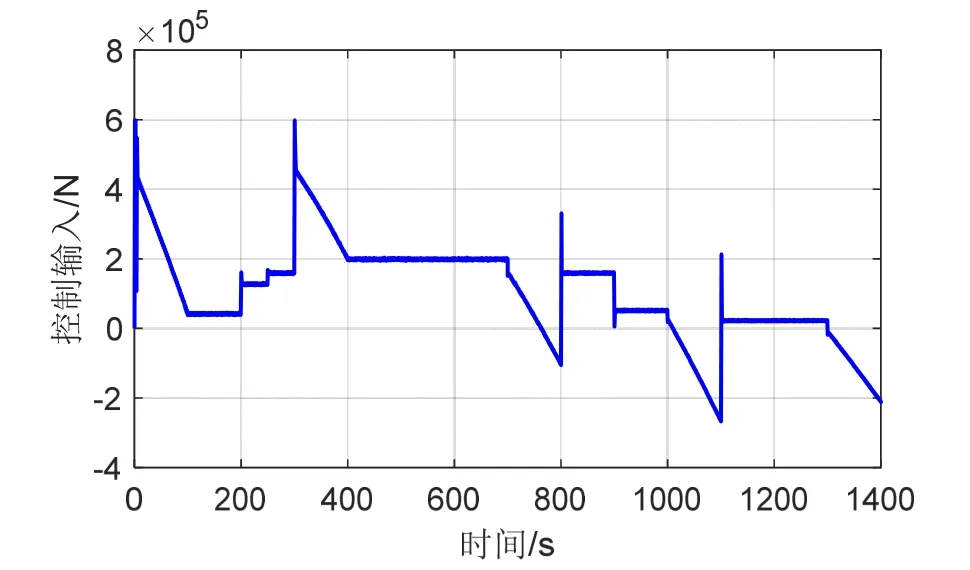
图3 列车控制输入（F）Fig.3 Train control input (F)

图4 控制输入变化率（0-6 s）Fig.4 Rate of control input（0-6 s）

为了验证所设计控制器抵御执行器故障以及系统不确定性的能力，对如下情况进行了仿真：1）列车运行至250 s时，执行器首次发生故障，执行器健康系数kc=0.9，运行至900 s时，执行器故障程度加重，相应的健康系数变为kc=0.7；2）其他阻力和坡度角分别增大到o(·)=5000sin(0.02vt)和θ=1.2*π/180°，3）参数的时变不确定性增加为原来的2倍。此时列车的跟踪误差曲线如图5所示。

图5 执行器故障变化及系统不确定性增大时的列车速度和位移跟踪误差Fig.5 Velocity and position tracking errors of train with varying actuator faults and increasing uncertainty

可以看出所设计的容错跟踪控制器具有很强的抵御系统不确定性以及执行器故障的能力，显示了系统良好的容错跟踪性能。

4 结论

本文通过引入双曲正切函数构造辅助系统，构建了列车的增广跟踪控制系统模型，并结合动态面控制方法和自适应控制技术，设计了高速列车的鲁棒容错跟踪控制算法，解决了列车受到执行器故障、输出幅值和变化率饱和等执行器性能约束，模型参数不确定性，以及附加阻力干扰等影响下的跟踪控制问题。所设计的控制器不依赖于列车质量、基本阻力系数、附加阻力，以及执行器故障等信息，可以有效补偿由模型参数不确定、附加阻力和执行器故障构成的不确定性。基于Lyapunov稳定性理论对系统的稳定性进行了理论分析，通过仿真结果对系统的可行性和有效性进行了验证。仿真结果表明，所设计的控制器在满足执行器输出幅值和变化率饱和约束的前提下，对于执行器效率部分损失故障、系统集总不确定性等具有很强的鲁棒性，表现出了良好的容错跟踪控制性能。