贯流泵导叶应力应变及振动特性数值模拟
施伟,李加旭,李松柏,孙涛,范雪梅,成立,罗灿
(1.南水北调东线江苏水源有限责任公司,南京 210029;2.扬州大学水利科学与工程学院,江苏 扬州 225009)
泵是一种能够将机械能转化为液体动能并实现定向输送液体的装置,在诸多领域得到了广泛应用[1]。其中,贯流泵由于其效率高,水力性能好,结构紧凑等优点,广泛应用于低扬程泵站中[2]。相比于轴流泵以及混流泵机组,在相同的开挖条件下,贯流泵机组可以减小厂房开挖量以及混凝土的使用量,降低泵站的总体造价[3-4]。同时因其机组为卧式布置,流动条件好,水力损失小,相比立式机组,贯流泵厂房结构简单且不用采用复杂的多层结构,降低了整体造价,被广泛应用于平原地区调水工程。
近年来,国内外诸多学者[5-7]对贯流泵内部流动进行了研究。随着计算机技术的发展,计算流体力学(computational fluid dynamics,CFD)与计算固体力学(computational solid mechanics,CSM)结合的流固耦合计算方式具有耗时短、成本低且易于获得流场中的流动数据与固体数据等优点,较多运用于计算流体机械内部的流体与固体的相互作用。王新等[8]通过在有限元框架内建立泵站非定常湍流和结构相互作用的流固耦合模型,对大型泵站单流道进行流固耦合振动分析,预测出各个部位的振动响应;吴新等[9]应用Ansys WorkBench软件,采用单向流固耦合的方法,模拟了不同工况下高扬程后置灯泡式贯流泵叶轮部分的应力应变情况;张新等[10]对某卧式双向全调节轴流泵在正向抽水工况下不同叶片转角的叶轮强度进行了单向流固耦合计算,得到了叶轮应力最大值和集中分布位置与扬程变化的关系;胡文竹[11]为了提高斜轴伸贯流泵装置的水力运行稳定性,研究了其不同流量下叶轮叶片的流固耦合动力学特性;梁武科等[12]对两种混流式水轮机展开顺序流固耦合分析,证明了转轮在小流量工况下的应力应变较小,而在设计工况以及大流量工况下的转轮应力应变较大。目前国内采用单向流固耦合的方法对卧式贯流泵分析的文献较少,且研究对象主要集中在泵的转轮叶片,对后置导叶的流固耦合分析较少。鉴于此,利用CFD商业软件CFX与CSM商业软件Static Structural结合的方法,对国内某卧式灯泡贯流泵在不同流量工况下的固定导叶进行单向流固耦合计算,分析导叶片表面等效应力分布和应变情况随流量的变化结果,计算贯流泵导叶片的湿模态特性,研究不同流量工况对导叶片的固有频率和振型的影响,为优化设计贯流泵导叶以及提高贯流泵运行稳定性提供参考依据。
1 数学模型
1.1 流场计算模型
一般认为流体在泵站和泵装置内的流动为三维不可压缩黏性湍流,故采用三维定常不可压缩雷诺时均N-S方程和κ-ε湍流模型对其内部的三维紊流场进行CFD数值模拟[13-14]。控制方程中的连续性方程为

动量方程为

式中:i、j=1、2、3;ui为速度矢量,m/s;p为压强,Pa;ρ为流体密度,kg/m3;υ为运动黏度,m2/s;f i为流体的体积力,N。
1.2 结构应力与模态分析计算模型
静力结构分析,主要考虑固体结构在静力荷载作用下的响应,重点关注的是结构的约束反力和应力、应变等参数。基于有限元的线性结构动力平衡方程为

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;ü、˙u、u分别为等效节点的加速度(m/s2)、速度(m/s)和位移(m);Et为结构应力引起的等效节点荷载向量,N。
模态分析基于牛顿第二定律。忽略阻尼系数后,当结构体外部激励为0时,其结构体的模态振动方程为

方程的形式解为

式中:ϕ为系数矩阵;i为虚部单位;ω为常数;t为自变量。
联立式(3)和式(4)得到自由模态的特征方程为

式中:λ=ω2。假设结构体的自由度为n,λ为结构体的某个特征值,则ω为结构体该阶的固有频率。
1.3 流固耦合求解方法
流固耦合将计算流体力学(CFD)与计算固体力学(CSM)结合,计算固体在流体作用下的应力应变及流体在固体变形影响下的流场的改变[15]。采用单向流固耦合方法开展研究,暂不考虑固体变形对流体的影响[16-17]。
2 流场数值模拟
2.1 物理模型
针对卧式灯泡贯流泵站,建立包括进水流道、叶轮体、导叶体和出水流道在内的过流部件模型。模型的几何参数:叶轮直径3 350 mm,叶片数3,叶片安装角0°,导叶体的叶片数7。基本性能参数:设计流量为37.5 m3/s,转速为115.4 r/min。流体区域模型及其网格见图1。采用mesh软件对该模型的流体区域进行网格划分,由于流道结构较为复杂,流体计算区域均采用非结构化网格,并对叶轮和导叶部分进行了局部网格加密。加密后的流体区域网格单元总数为6 537 251个,其中叶轮部分计算网格数量为38万个,导叶部分网格数量为85.5万个。

图1 卧式灯泡贯流泵三维模型及其网格Fig.1 3-D model of horizontal bulb tubular pump and mesh of fluid domain
2.2 边界条件与瞬态计算设置
分别对流体域和固体域进行边界条件设置。流体域部分:进水流道入口设为质量流量进口,设置出水流道的出口断面处为自由出流的边界条件,所有壁面采用绝热无滑移边界,流体介质为水,各个不同流域之间采用交界面进行连接。采用k-ε湍流模型及SIMPLEC算法。在流体区域计算完毕后,将计算结果导入商业软件Static Structural中,并将叶轮和导叶材料均设置为结构钢[11]。
为了分析不同工况贯流泵内部的湍流流态对导叶叶片的影响,需要对5种不同流量工况下的贯流泵流场进行瞬态计算。这5种工况分别为0.6Qd、0.8Qd、1.0Qd、1.2Qd、1.4Qd,其中Qd为设计流量。设置计算总时间为5.199 31 s(叶轮旋转10周),时间步长为8.665 5×10-3s(叶轮旋转6°)。基于收敛后的瞬态数值模拟结果,进行单向流固耦合计算。
3 结果分析
3.1 水泵性能试验结果与数值模拟结果
原型泵的性能试验结果与数值模拟结果见图2,通过对比发现二者性能曲线变化趋势完全一致,且最高效率点基本吻合,误差小于5%,这说明数值模拟结果是可靠的。
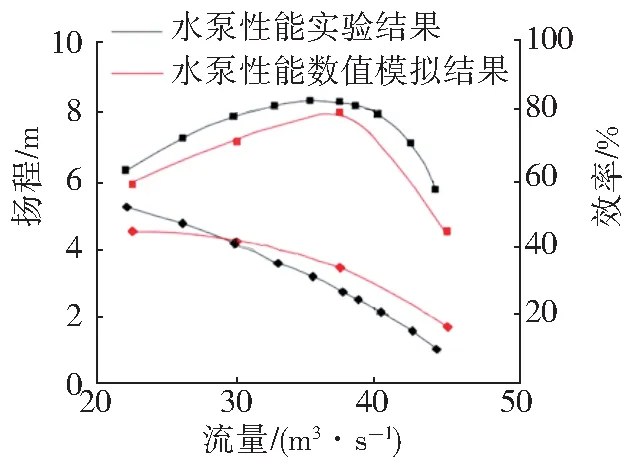
图2 水泵性能实验结果与数值模拟结果Fig.2 Pump performance experimental results and numerical simulation results
3.2 最大应力应变数值分析
基于Static Structural模块,得到单向流固耦合条件下不同工况导叶的最大等效应力和最大应变量见图3。导叶上最大的等效应力值出现在0.8Qd工况附近,约为30.371 MPa,小于所选材料的极限抗拉强度,满足强度要求。
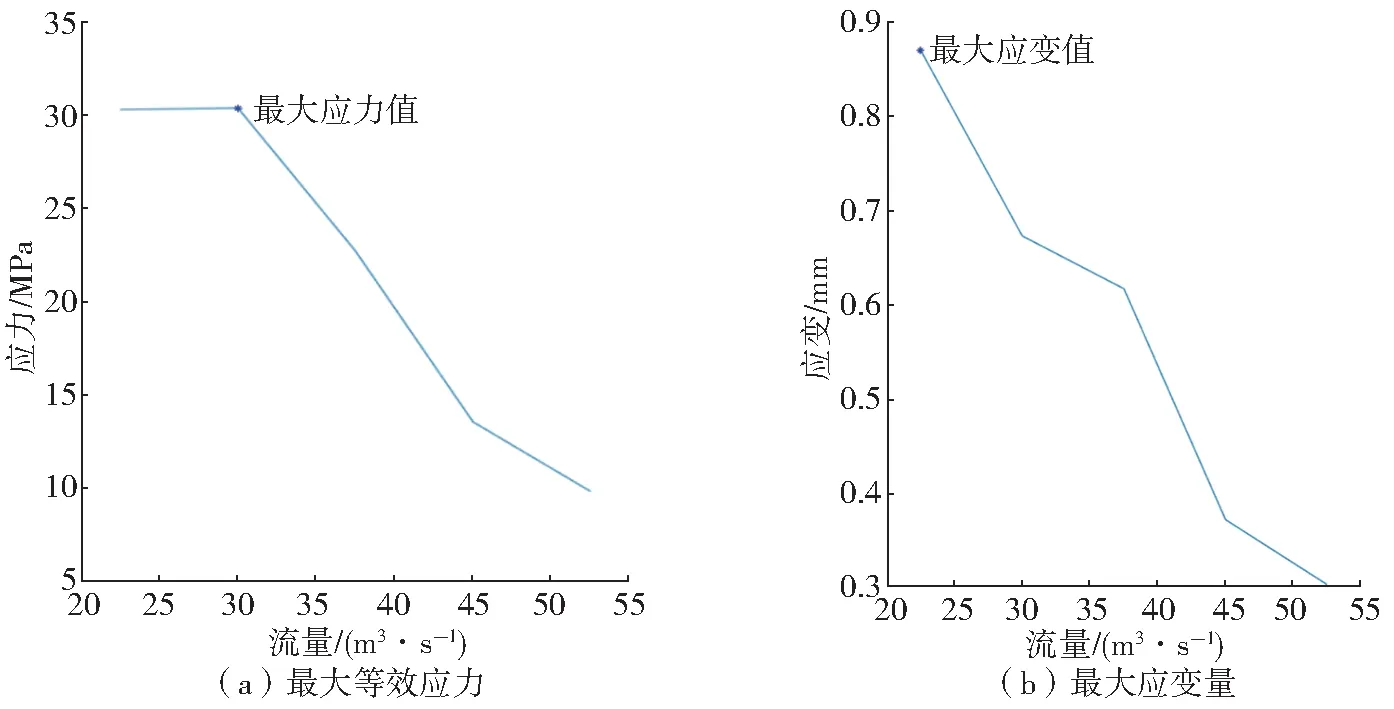
图3 最大等效应力和最大应变量随流量变化Fig.3 Maximum equivalent stress and maximum strain changing with flow rate
3.2.1 等效应力分析
导叶在0.6Qd(小流量)工况下、1.0Qd(设计流量)工况下以及1.4Qd(大流量)工况下的等效应力分布见图4。

图4 3种流量工况下等效应力分布Fig.4 Contour of equivalent stress under three conditions
由图4(a)可以看出,在小流量工况(0.6Qd)下,导叶叶片压力面等效应力发生在导叶片根部进出水侧以及导叶片外缘中部,其较大的等效应力主要发生在导叶进口根部,约占压力面的20%,而在导叶叶片的吸力面,小流量工况下流体产生的等效应力面主要集中在导叶中下部分,面积约为整个吸力面的40%,但应力数值较小,相对较大的等效应力发生在导叶中下处根部。根据图3可知,在该工况下的导叶叶片所受到的最大等效应力,为5种工况下的最大值。由于流量较小,导叶片对流体的整流效果较好,水流在导叶流道的后半段几乎完全沿着导叶片流动,不再对导叶片有较大的冲击,所以导叶片表面的后半段没有出现大范围的等效应力集中区。
图4(b)显示,在设计工况下,导叶叶片上的等效应力分布和小流量工况下的没有明显区别:均是在导叶叶片压力面根部的进出水侧以及外缘的中段出现等效应力集中区;在叶片吸力面中下部分出现大范围等效应力的集中,面积略有扩大,且较大的等效应力仍发生在导叶中下处根部。相对小流量工况,设计工况下的最大等效应力数值有所降低,这是因为设计工况下导叶流道内的流态理应是5种工况下最好的。
图4(c)显示,在大流量工况(1.4Qd)下,导叶上的等效应力数值及分布较之前2个工况有了较大的变化:从数值上看,1.4Qd流量下的最大等效应力及应变数值是5种工况中最小的,仅为9.855 MPa和0.302 mm;从等效应力分布上看,其在导叶压力面上的分布不再是相对独立的应力集中区,而是沿着整个导叶片根部区域分布,且较大的等效应力同时出现在压力面进出口根部处,分布范围约占整个压力面的60%;在导叶片的吸力面,等效应力集中区扩散至整个叶片吸力面90%的区域,较大的等效应力同样集中在导叶片根部位置。从云图分析来看,虽然在大流量偏工况运行下,水流对导叶片造成的应力数值相比其余工况更小,其水流流态更不容易被导叶调整,因此形成了沿着导叶根部贯穿整个导叶并从导叶出口延伸至轮毂上的应力集中区,说明此时导叶的整流作用相对较小且效果最差。
3.2.2 导叶表面截线上压力分布
为了更直观地分析导叶压力面上的等效应力分布和变化情况,采用截线分析的方法,从导叶进口到出口方向上,分别在导叶0.9R(外截线)和0.1R(内截线)(R为轮毂至导叶外缘长度)处投影截线[18](图5),并将同一截线上3种工况下的等效应力数值绘制在图上,见图6。

图5 内外截线及其应力观测点Fig.5 Schematic diagram of internal and external sections and stress observation points
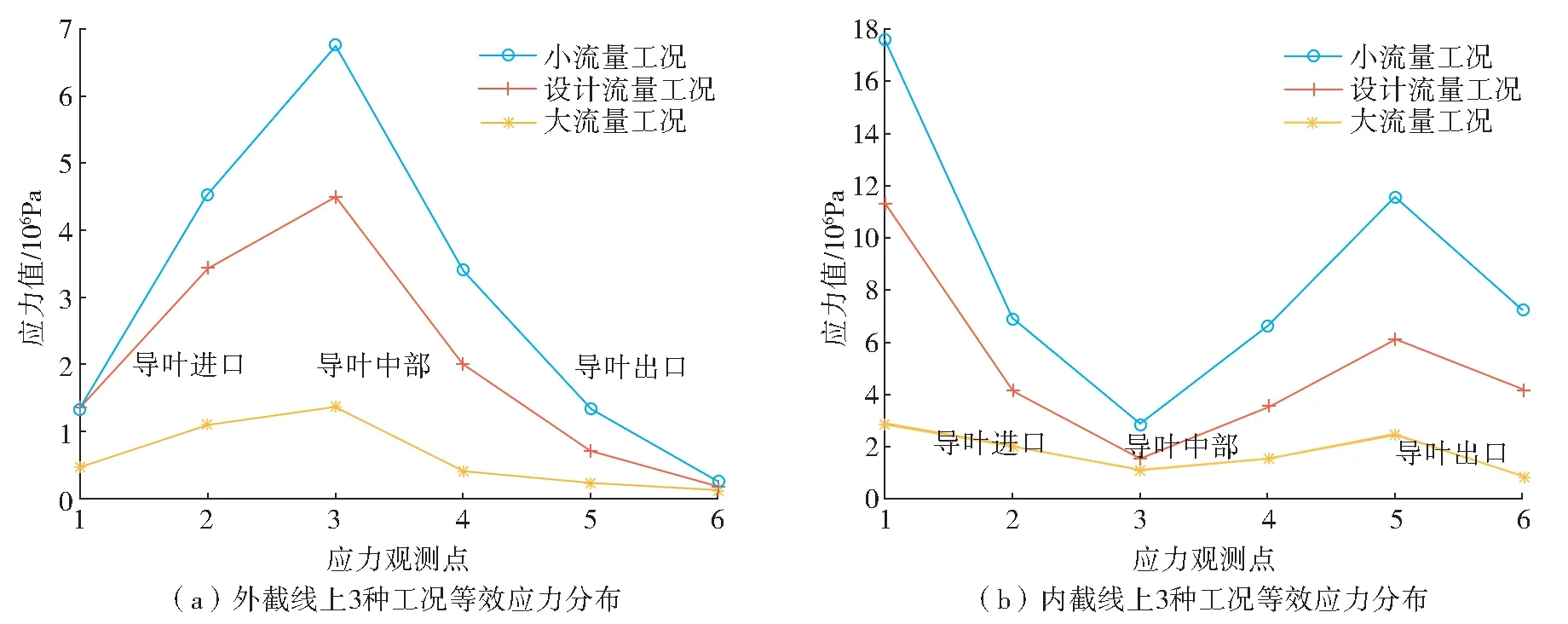
图6 两条截线上不同工况应力分布Fig.6 Stress distribution maps of different working conditions on two sections
通过图6(a)可以看出,3种工况下的等效应力数值在导叶距离轮毂0.9R处,即导叶外缘处沿着水流方向先上升后下降,最大值点均出现在导叶顺水流方向的中间部位。小流量工况下的整体等效应力数值要大于另外两种工况,同时在顺水流方向上的数值变化程度也最剧烈;设计流量和大流量工况下的等效应力数值分布趋势基本与小流量工况保持一致,但是大流量工况下的应力变化程度相对另外两种工况较为平缓。
图6(b)显示,在导叶距轮毂0.1R处的等效应力数值在顺水流方向上呈现先下降后上升再下降的趋势,最小值点均出现在导叶片沿着水流方向的中间部位。整体等效应力的数值依旧是在大流量工况下最小,且变化程度最缓。
截线压力数值分布与图4分析结果吻合良好。综上,导叶进出水侧与轮毂的连接处以及导叶外缘中部等效应力较为集中,易发生疲劳破坏,需重点关注。
3.2.3 总体应变分析
导叶在0.6Qd(小流量工况)、1.0Qd(设计流量工况)以及1.4Qd(大流量工况)下的应变分布云图见图7。

图7 不同工况下导叶片应变云图Fig.7 Strain contour of guide vane under different conditions
小流量工况(0.6Qd)和设计工况(1.0Qd)下,导叶片较大的应变主要集中在导叶片外缘进口位置,导叶片根部并无明显应变出现,且最大应变数值在小流量工况时最大,达到了0.869 mm,整体应变区域占导叶面积的40%以上;大流量工况下的导叶片的较大应变集中区域相比其余工况有了明显变化,出现在了导叶片外缘出口位置,且最大应变数值最小,整体变形区域约占叶片面积的60%。
导叶片应变云图的展示了随着流量的增大,流体使导叶产生的应变减小,但是最大应变位置上移,同时,不同流量工况下的导叶片应变区域总是集中在叶片的外缘,叶片根部并无明显应变产生。这一点对研究水泵导叶的优化设计有一定参考意义。
3.2.4 湿模态分析
使用WorkBench研究不同流量工况对导叶片的固有频率和振型的影响,对该模型导叶片施加流体应力的前10阶湿模态进行计算[19-20]。小流量工况、设计工况、大流量工况下,导叶前10阶湿模态对应的固有频率数值见表1和图8。

表1 3种工况下导叶前10阶湿模态对应的固有频率Tab.1 First ten steps results of wet modal under three working conditions 单位:Hz
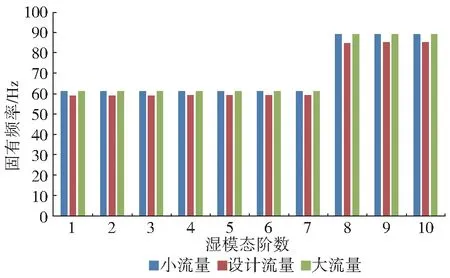
图8 不同工况下湿模态前10阶固有频率Fig.8 First ten steps natural frequencies of wet mode under different working conditions
从表1和图8可知:随着计算阶数的增加,在第7阶振型之前,导叶片在3种工况下的固有频率稳定增加,但是其变化幅度不大;从第7阶振型之后,导叶固有频率陡然增大。由于导叶片本身处于相对较差的流态(图9)中,所以其自第1阶模态开始,固有频率就较大,变形也较为严重。前7阶的固有频率在同阶模态下均略有增大(约为3.5%),而在第7阶之后,同阶模态下的非设计工况固有频率比设计工况下的固有频率增大了约5%。这说明非设计流量工况对于导叶片的固有频率影响有限,可以认为不同的流量对于导叶片的频率影响较小,在后续进行共振风险分析时可以忽略不计。

图9 叶轮导叶部分的流线Fig.9 Flow chart of impeller guide vane
图10为设计流量下导叶湿模态第2、4、6、8、10阶的振型,从图中可以明显看出各阶模态下的导叶片变形区别:在第2阶、第4阶、第6阶中的变形集中在导叶片外缘的中上部,在导叶外缘出口处最大,而在第8阶振型以后,导叶的振动变形主要集中在导叶片外缘的中下部。

图10 设计流量下的导叶振型Fig.10 Vibration mode of guide vane under design flow
4 结 论
本文采用单向流固耦合方法开展了贯流泵导叶应力应变及振动特性的数值模拟研究,主要结论如下:
随着流量的增加,导叶表面等效应力与应变量均趋于减小。
在设计流量和小流量工况下,导叶压力面的等效应力分布区域基本一致,位于导叶进、出口的根部和外缘中部,其大小约占导叶的40%,大流量工况则与之差异较大,由导叶进、出口根部向中部延伸,其大小约占导叶的90%。建议设计贯流泵导叶时应重点关注导叶根部的等效应力。
在不同流量工况下,导叶叶片间的应变分布差异明显,各叶片的大应变区主要集中在导叶外缘,导叶根部无明显应变。建议设计贯流泵导叶时应重点关注导叶外缘的应变量变化。
通过分析导叶前10阶湿模态计算结果发现,导叶各阶振动频率与流量因素相关度不高,导叶振动频率的值会随着阶数增加而增加,但增幅不大,因此共振风险分析可以忽略流量变化对其振动频率的影响。

