丹江口水库水面蒸发变化特征及影响因素

白鹏，刘小莽，刘璐，董剑萍

（1.中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室，北京 100101；2.宁夏回族自治区盐池县水务局，宁夏 盐池 751500）

水体（湖泊、水库、池塘）蒸发是全球水循环的重要组成部分，在全球水循环和能量循环中发挥着重要作用。据统计，全球面积大于0.1 km2的水体超过300万个，约占全球陆地面积的3%［1］。在北半球一些国家，水体占国土面积比例接近甚至超过10%。水体蒸发是湖泊、水库等水体水量损失的主要方式。Vardavas等［2］分析指出，澳大利亚大型水库的年蒸发损失占水库蓄水总量的20%左右。我国新疆北部平原区大型水库年蒸发损失占水库总蓄水量的40%［3］。因此，水面蒸发的科学估算一直是水文学和气候学研究的热点之一［4-6］。

水面蒸发主要受两类因素的影响：一类是水体上方的气象条件，如太阳辐射、温度、湿度、风速等；另一类是蒸发面的自身因素，如水体的反照率、水深、水质和周边的地形等。开阔水体的蒸发很难直接测量，通常采用各种间接方法来估算。常用的水面蒸发估算方法包括蒸发皿折算法、水量平衡法以及基于气象要素的估算方法［5，7］。蒸发皿折算法［8］是估算水体蒸发最简单且成本最低的方法之一，该方法通过布设于水体周边的蒸发皿观测值乘以折算系数来估算水体蒸发。蒸发皿折算法的缺点在于蒸发皿折算系数难以准确确定，该系数取决于蒸发皿的类型、布设位置和水体周边地形等诸多因素，具有很强的时空异质性［9］。水量平衡方法将水体蒸发视为水量平衡的残差项，通过测量或估算其他水量平衡项（如入流、出流、降水和储水量变化等）来估算蒸发［10］。水量平衡方法原理简单，但面临的主要问题是一些水量平衡项（如湖泊渗漏量、地下水补给量和储水量变化）很难被合理地测量或估算［11］。相对而言，基于气象要素的水体蒸发估算方法在实际应用中最广泛，代表性方法包括基于道尔顿水汽扩散原理的质量传输（Mass-transfer）法［10］、基于能量平衡原理的Priestley-Taylor法［12］以及兼顾水汽扩散原理和能量平衡的Penman类方法［4］。其中，Penman类方法综合考虑了影响蒸发的辐射项和空气动力学项，具有坚实的物理基础，适用于不同气候条件下的水体蒸发估算。

南水北调中线工程作为我国“四横三纵”水资源调配格局的重要“一纵”，是缓解华北地区水资源短缺的大型跨流域调水工程。目前，中线工程调度管理面临最大的挑战之一是水源区丹江口水库可调水量的不确定性。观测数据显示，丹江口水库1999—2014年入库年径流较工程论证期（1954—1998年）减少了73.6亿m3，占一期规划年调水量（95亿m3）的77.5%［13］。此外，丹江口水库水域宽阔，库区面积超过1 000 km2，水库蒸发损失量不可忽视。但是，鲜有文献量化丹江口水库的蒸发损失、识别引起水库蒸发损失的主控因素。基于此，在Penman类方法基础上，考虑水体热存储变化对蒸发的影响，定量估算丹江口水库蒸发损失的变化，定量揭示不同气象要素对水库蒸发趋势的贡献，研究结果可为中线调水工程的科学调度和水资源管理提供决策支持。

1 研究区和数据来源

丹江口水库位于长江流域最大的支流——汉江的中上游，地处豫西南和鄂西北交界处的山地丘陵区，控制流域面积95 217 km2，约占汉江流域总面积的60%。丹江口水库始建于1958年，竣工于1974年。由于调水的需要，水库大坝的加高工程自2005年开始施工，2013年正式完工蓄水。加高后的水库库区面积达1 022.75 km2，最大蓄水量达290.5亿m3［14］。2014年12月，南水北调中线工程正式通水，供水范围覆盖河南、河北、北京、天津等4个省（直辖市）20多座城市，直接受益人口近8 000万人，有效缓解了华北地区长期以来水资源严重短缺的局面。

气象数据来源于国家气象信息中心（https：／／data.cma.cn／），包含4个国家标准气象站逐日温度、湿度、风速和日照时数等数据。考虑到气象站高程和水面高程的不一致，采用经验公式［15］修正了高程对气象要素（温度、饱和水汽压以及风速）的影响。净辐射数据通过日照时数数据和FAO-56 Penman-Monteith方法［16］计算，计算过程中水体的反照率设置为0.08［17］。2001—2019年逐月的水库水域面积数据来源于全球水库表面积数据集（https：／／dataverse.tdl.org／dataset.xhtml？persistentld＝doi：10.18738／T8／DF80WG），该数据集基于一个图像增强算法修复了受云污染的Landsat影像［18］。此外，泰森多边形方法被用来确定每个测站控制水域面积的权重。

开阔水面蒸发很难直接测量，因此水面蒸发估算的验证是长期困扰学术界的难点之一。世界气象组织建议将20 m2及以上的大型蒸发池观测的蒸发作为（浅水）开阔水面蒸发估算的验证数据［19］。但是，大型蒸发池的安装与维护需要大量的人力和财力成本，此类观测站点分布稀少。我国气象站点普遍采用直径20 cm或60 cm（E601）的蒸发皿观测表征大气的蒸发能力，再通过蒸发皿折算系数估算开阔水体的蒸发。本文在站点尺度上评估了Penman类方法计算的水库蒸发的可靠性。4个气象站点中，丹江口站提供了2007—2019年E601蒸发皿（直径60 cm）观测的蒸发值，参考文献［20］将研究区E601蒸发皿水面蒸发折算系数设置为0.95，据此可估算出该站点气象条件下的开阔水体蒸发量。

2 方法和模型

2.1 耦合平衡温度的Penman模型

水体蒸发估算方法最早可追溯到1802年道尔顿提出的经验方程，该方程认为水体蒸发主要取决于水体上方的水汽压差和风速［10］。1926年，Bowen［21］从能量平衡原理出发，提出了计算蒸发的波文比-能量平衡法。1948年，Penman［4］综合考虑了影响水体蒸发的能量条件和水汽扩散条件，提出了具有划时代意义的Penman模型。该模型最初是为了估算开阔水体蒸发而设计的，后续的许多蒸发模型，如Penman-Monteith模型［22］和Priestley-Taylor模型［12］，都是基于Penman模型的理论框架而构建的。Penman模型计算水体蒸发（Eow）的表达式为

式中：λ为水汽蒸发潜热，kJ／kg；Rn为净辐射，MJ／（m2·d）；γ为干湿计常数，kPa／；Δ为饱和水汽压曲线的斜率；es和ea分别为饱和和实际水汽压，kPa；G为水体热存储变化，MJ／（m2·d）；f（u）是风速函数，原始的f（u）＝2.6（1＋0.536u2）［4］，其中u2表示2 m处风速，m／s。1956年，Penman［23］基于一个湖泊蒸发观测的结果对原始风速函数进行了修正：f（u）＝2.6（0.50＋0.536u2）。本文采用修正的风速函数计算水面蒸发。

水体热存储变化很大程度上影响短历时（日或小时）的蒸发估算。一些研究［7，24］表明，在蒸发计算过程中考虑水体热储量变化能够提高模型的计算精度。本研究将平衡温度模型耦合到Penman模型中，考虑热储量变化对水体蒸发的影响。平衡温度是指当水体和空气界面之间的净热交换为零时的温度［25］。该方法主要适用于没有明显温度分层的水体，暗含的假设是水温在垂向上没有变化［26-27］。在此基础上，水温（Tw）可以表达为时间常数（τ）和水深（zw）的函数，G可根据逐日水温的变化估算，具体的计算公式为

式中：ρ为水体密度（ρ＝1 000 kg／m3）；c表示水的比热容（c＝4.2×10－3MJ／（kg·℃））；Te为平衡温度，℃；Tw0为前一日水温，℃；Tn为湿球温度，℃；是湿球温度下的净辐射，MJ／（m2·d）；Δw是湿球温度下饱和水汽压曲线斜率，kPa／℃。

2.2 蒸发变化的归因分析和模型评估指标

基于去趋势方法定量分析不同气象要素（温度、净辐射、相对湿度和风速）对蒸发变化的贡献。去趋势方法在年尺度上去除气象要素的趋势项（年序列趋势为零），但保留要素的季节性波动。以温度要素为例，具体的步骤［28］如下：将年温度序列进行去趋势，得到逐年的调整系数；将逐日温度数据乘以该年的调整系数得到调整后的逐日温度序列；保持其他模型驱动数据不变，将原始的和去趋势的日温度序列分别输入Penman模型中，年蒸发趋势的差异可归因为温度变化的影响。

基于同样的步骤，可以依次计算净辐射、相对湿度和风速变化引起的蒸发趋势差异。同样以温度为例，其对蒸发趋势的贡献度C为

用到的3个模型表现性评估指标，分别为确定性系数（R2）、相对偏差（Br）以及Kling-Gupta系数（KGE）。R2描述了模拟值对观测值变化的解释程度，最优值为1.0；Br衡量了模拟变量大于或小于观测值的平均趋势，最优值为0；KGE作为一个综合的评估指标来衡量观测值和模拟值的拟合程度［29］，最优值为1.0。3个指标的计算公式为

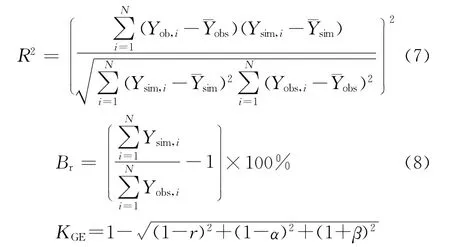
其中，

式中：Yobs为观测值；Ysim为模拟植；ˉYobs为观测序列的平均值；r为相关系数；σs和σo分别为观测值和模拟值的标准差；β是模拟植和观测值平均值的比值；N是观测值或模拟值序列长度。

3 结果和讨论

3.1 丹江口水库库区气候要素和水体面积的演变特征

图1展示了影响水体蒸发的4个关键气象要素（温度、净辐射、相对湿度和风速）的年际变化。平均气温和净辐射均呈显著（p＜0.05）上升的趋势，趋势值分别为年上升0.07℃和0.27 W／m2，且二者的年际波动较一致，高温年的净辐射值也较大。相对湿度呈不显著的（p＞0.05）减少趋势，而平均风速呈显著（p＜0.05）增加的趋势，二者的趋势值分别为每年减少0.07%和每年增加0.007 m／s。从要素的趋势而言，4个气象要素的变化都有利于水面蒸发的增加。

图1 2000—2020年丹江口水库库区温度、净辐射、相对湿度和平均温度的年际变化Fig.1 The interannual variability of temperature，net radiation，relative humidity，and wind speed in Danjiangkou Reservoir from 2000 to 2020

图2展示了丹江口水库水面面积2000—2020年的逐月变化以及年际波动。丹江口大坝加高工程2013年主体工程完工并开始蓄水，2015年以后水库的水域面积迅速增加。水库水面面积最大值达到442.8 km2，出现时间是2020年2月，最小值为206.7 km2，出现在2014年4月。2000—2014年，水库水面面积呈不显著（p＞0.05）减少的趋势，趋势值为每年减少0.7 km2，多年均值为345.9 km2。2015—2020年，得益于水库大坝的加高工程，水库水面面积呈增加趋势，年增加8.4 km2，多年均值为408.9 km2。2015年以后，由于中线供水的需要，水面面积的年内波动明显变小。逐月的水域面积在350～450 km2，波动范围（100 km2）显著小于2000—2014年的波动范围（200 km2）。

图2 2000—2020年丹江口水库水域面积的逐月波动和年际变化Fig.2 The monthly fluctuations and interannual variability in surface water area of Danjiangkou Reservoir from 2000 to 2020

3.2 水面蒸发的验证

基于丹江口站蒸发皿（E601）蒸发折算值为参考，在站点尺度上评估了Penman模型的水面蒸发模拟结果见图3。由图3可知，Penman模型模拟的蒸发值和参考值能够很好地吻合。模拟值和参考值的R2、Br和KGE分别为0.88、1.3%和0.92。因此，耦合平衡温度的Penman模型可以作为一个可靠的工具来模拟丹江口水库水面蒸发变化。

图3 Penman模型模拟的水面蒸发值和E601折算的水面蒸发值的比较Fig.3 Comparison of open-water evaporation simulated by the Penman model against evaporation estimates converted from E601 observations

3.3 水面蒸发和水库蒸发损失量的变化特征

基于耦合平衡温度的Penman模型模拟了丹江口水库2000—2020年的逐日水面蒸发，并结合水域面积估算了水库的蒸发损失量。丹江口水库水面蒸发的年内波动与其温度和辐射一致，通常在7月份最高，1月份最低，见图4。多年平均的水面蒸发量为726.6 mm／a，最大值（770.0 mm／a）出现在2013年，最小值（663.4 mm／a）出现在2003年，见图5。年水面蒸发呈不显著（p＞0.05）的增加趋势，趋势值为1.55 mm／a。

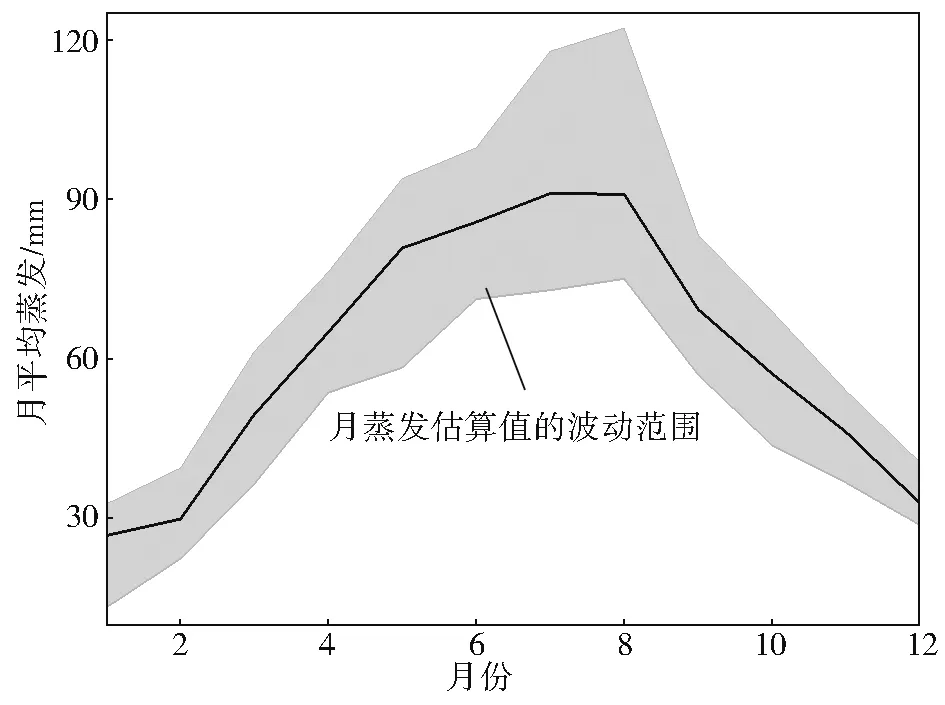
图4 水库水面蒸发的季节性波动特征月蒸发估算值的波动范围Fig.4 The seasonal cycle of open-water evaporation in Danjiangkou Reservoir.

图5 水库水面蒸发量和水库蒸发损失量的年际变化Fig.5 The interannual variability in open-water evaporation and evaporation loss in Danjiangkou Reservoir

2000—2020年，水库的蒸发损失量呈现显著（p＜0.05）增加的趋势，趋势值为0.034亿m3／a。多年平均的水库蒸发损失量为2.6亿m3／a，最大值（3.2亿m3／a）出现在2018年，最小值（2.2亿m3／a）出现在2011年。水库的蒸发损失量不仅与水面蒸发有关，还取决于水库的水域面积。2015年以后，随着水域面积的增加，水库蒸发损失量也显著增加。以2015年为时间节点，前后两个时期的水库蒸发损失量分别为2.4亿和3.0亿m3／a，水库蒸发损失的增加量（0.6亿m3／a）主要由水域面积的增加贡献。在水域面积不增加的情景下［即2015—2020年水域面积为多年（2000—2014年）平均值］，水库的蒸发损失量为2.5亿m3／a，水域面积变化对水库蒸发损失增加的贡献为82%。以一期工程规划调水规模（95亿m3／a）计算，水库多年平均的蒸发损失量占调水规模的2.7%。但实际的工程调水量远小于规划的年调水量。截至正式通水7周年时（2021年12月12日），南水北调中线工程累计调水441亿m3，折合63亿m3／a［30］。以此计算，水库年平均的蒸发损失量占年调水量的比例为4.8%。在气候变暖背景下，随着大气蒸发能力的增强，丹江口水库的蒸发损失可能会进一步加大。建议有关部门在今后的水资源规划中充分考虑水库蒸发损失对可调水量的影响。

3.4 水库水面蒸发的控制因素及趋势贡献

基于公式（6），定量解析4个气象要素（温度、净辐射、相对湿度和风速）对水库水面蒸发趋势的贡献见图6（a）。结果表明：水库水面蒸发趋势由净辐射变化主导，其贡献度为72.0%；其次为温度变化，贡献度为23.6%，相对湿度和风速变化对水库蒸发趋势的贡献很小，其贡献度分别为2.7%和1.7%。为了进一步探究不同气象要素相对贡献差异的原因，分析蒸发估算对4个气象要素波动的敏感性。分别对4个气象要素施加±5%和±10%的干扰，再分别输入到蒸发模型中计算4个干扰引起的年蒸发的相对变化，年蒸发相对变化的线性拟合值即可表征蒸发对该要素干扰的敏感性，见图6（b）。结果发现，水面蒸发估算对净辐射变化的响应最敏感，其敏感性指数为2.14，即净辐射每增加10%，将引起21.4%的蒸发增加。蒸发对其他要素的敏感性排名依次为温度（0.80）、相对湿度（－0.55）、风速（0.12）。基于敏感性试验和要素的变化趋势，4个气象要素对水面蒸发趋势的相对贡献就可以很好地加以解释。

图6 气象要素对水库水面蒸发年趋势的贡献以及水面蒸发对气象要素的敏感性分析Fig.6 The contribution of meteorological factors to the annual trend of open-water evaporation and the sensitivity analysis of open-water evaporation estimates to meteorological factors

4 结 论

基于Penman类方法和水域面积定量估算了丹江口水库2000—2020年的水面蒸发和蒸发损失量变化，解析4个气象要素对水面蒸发趋势的贡献，主要的研究结论如下：

2000—2020年，丹江口水库水域面积呈显著（p＞0.05）增加的趋势，特别是2015年大坝加高蓄水后，水域面积增加明显。

2000—2020年，水库水面年蒸发量呈不显著（p＞0.05）增加趋势，多年平均蒸发量为726.6 mm／a。水库蒸发损失量呈显著（p＜0.05）增加趋势，多年平均的蒸发损失量为2.6亿m3／a，占规划年调水量（95亿m3）的2.7%。中线工程实际运行前7年，水库年平均蒸发损失占年平均调水量的比例为4.8%。

净辐射变化对水库水面蒸发趋势的贡献度最大（72.0%），其次为温度（23.6%）、相对湿度（2.7%）和风速（1.7%）。