有限理性视野下出行者停车场选择研究
王志美 辛 涛 徐 菱* 韩 健 叶 海 杜 宇
(西南交通大学交通运输与物流学院1) 成都 611756) (成都交通信息港公司2) 成都 610041)
0 引 言
由于有限的城市用地,停车问题不能单纯地通过修建新的停车位来解决,研究表明,驾驶员停车选择是一个受诱导信息影响的博弈过程[1],因此,如果平台能够诱导区域内车辆合理停泊,可以减少城市道路交通压力,实现停车场泊位资源的均衡利用,改善停车难的问题.
针对出行者的停车选择行为研究,王韩麒等[2]通过考虑出行者选择停车场时的影响因素,构建模型为出行者选择最优停车场.贺康康等[3]研究了在动态停车预约收费条件下,个人属性、出行特性、停车特征,以及建成环境对出行行为选择的影响.Ye等[4-5]研究表明:出行者在进行停车选择的过程中显著受到出行者感知到的停车费用的影响.陈鹏等[6]研究表明:当停车收费价格制定合理时,能有效改善城市交通状况.通过智能交通诱导平台制定停车收费标准可以很好的诱导驾驶员的停车选择,但目前在停车收费标准制定的过程中,还存在诸多问题.
目前,有学者从泊位资源均衡利用的角度研究出行者的停车场选择诱导模型.朱成娟等[7]从政府对停车位管理角度引入博弈模型研究停车位的分配与定价问题.文献[1]引入Stackelherg博弈理论分析停车管理者和驾驶员之间的博弈关系,在考虑驾驶员停车后步行距离最小的情况下,通过对高峰泊位空闲指数差异均值的控制,实现高峰停车泊位资源的均衡利用.王艳等[8]基于驾驶员角度,提出按出行费用高低依次选择停车场的原则,基于该原则,通过调整停车费率就能够使得各停车场利用率均衡.
在以上研究中,出行者往往被假定为完全理性的,在知道路况信息及停车场信息之后,出行者会优先选择费用最低的停车场.但实际上,Simon等[9-10]发现:人们决策时往往是追求满意结果而不是最优结果,出行者并不总是选择出行效用最大的交通方式,其选择行为与出行者的理性程度和偏好有关,即使在最理想的环境下,决策者的行为也会表现出明显的背离期望效用理论的现象.张新洁等[11]发现停车场费率的变化会影响出行者的出行方式选择,可以通过调整停车费率诱导出行者驾车出行,提高车位占有率.在有限理性视野下,不同于文献[8]按出行费用高低依次选择停车场的原则,城市管理者将在驾驶员可接受的费用区间内诱导停车场选择,避免车辆局部聚集,实现区域内停车泊位均衡利用的目标.
本文基于城市管理者的角度,在有限理性视野下,研究停车费率对驾驶员停车场选择的影响,通过调整停车费率,诱导驾驶员停车场选择,以此来改善车辆局部聚集的情况,实现区域内停车泊位资源的均衡利用.
1 模型构建
若某一时间段有Q位出行者在路口O前往目的地S,每位出行者在目的地附近有多个停车场可供选择,出行者综合整个出行过程的费用,当区域内停车费用一样时,费用敏感的一类驾驶员会倾向于选择停车后步行距离较短的停车场,这就会导致车辆局部集聚,前往该停车场的路段会出现拥堵,见图1a).若能合理的调整区域内停车场的费率,引导驾驶员的停车选择,就可以使车辆的流向均匀分配,提高路段的通行率及停车场的使用率,见图1b).
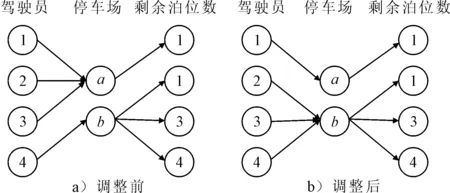
图1 停车费用调整前后停车场分配示意图
1.1 模型假设
1) 出行者的感知成本由固定项和随机项组成,随机项服从二重指数分布;出行者是有限理性的,出行效用的无差异阈值会影响出行者行为,若停车场之间的效用差大于无差异阈值,出行者的选择将服从随机效用最大化;若停车场之间的效用差小于无差异阈值,出行者将不能区分两者的大小,此时驾驶员根据偏好程度选择停车场.
2) 出行者由当前位置前往停车场的路段只考虑路段交通量对行驶时间的影响,不考虑行驶过程中信号灯的等待时间.
3) 假设所有出行者的无差异阈值及对选择的偏好程度相等,备选停车场的停车费率在出行者的接受范围内,只是对于不同的价格有不同的偏好程度.
1.2 BRNL模型推导
传统logit模型依据随机效用理论,假设出行者选择其所认知到的方案中效用最大的方案, 即驾驶员n选择停车场i的概率Pn(i)等价于事件Uin>Ujn发生的概率,即
Pn(i)=P(Uin>Ujn)=P(Vin+εin>Vjn+εjn)=
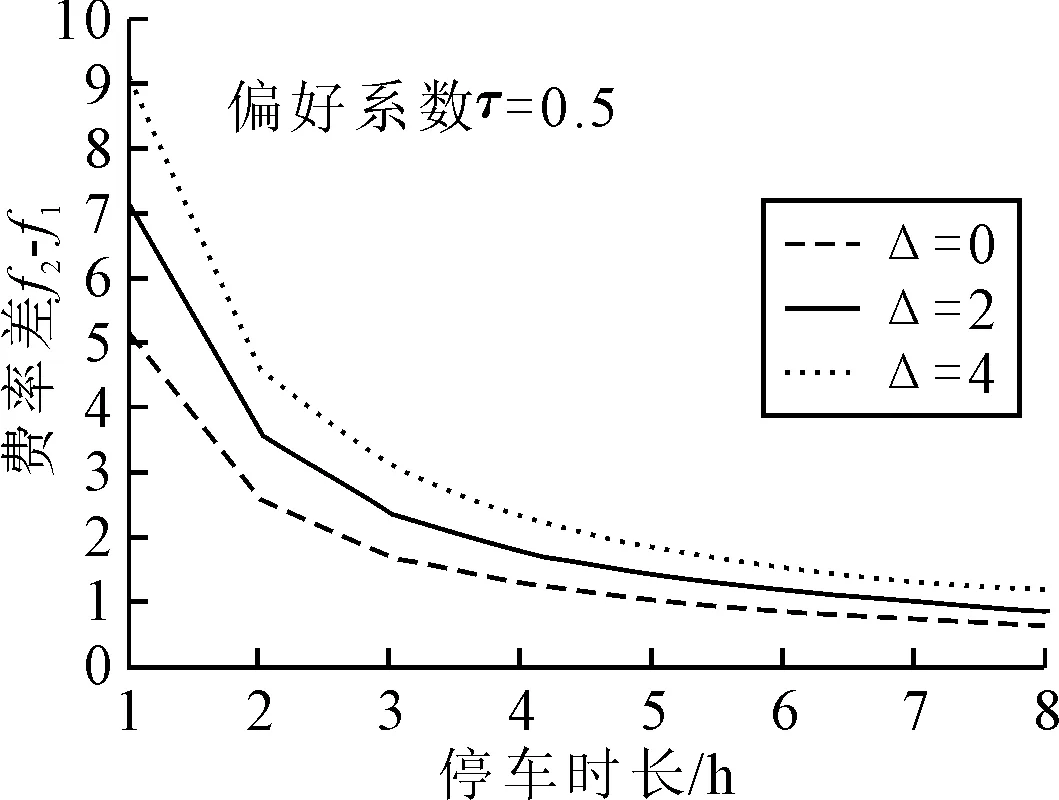
P(εjn-εin (1) 当随机变量εi和εj均服从(0,θ)的指数分布,且二者之间相互独立时,它们的εi-εj差便服从参数为(0,1)的指数分布,所以驾驶员n选择停车场i的概率Pn(i)为 (2) 本研究考虑驾驶员在有限理性的情况下选择停车场.即当停车场的感知成本差的绝对值小于无差异阈值时,出行者不能区分两个停车场的成本大小,将根据对停车场的偏好或随机进行选择;当停车场的感知成本差的绝对值大于无差异阈值时,出行者将选择感知成本最小的停车场.其中,当两个备选方案的效用差小于某一特定数值时,出行者对两种方案的感知相同,这一特定数值即为无差异阈值. 假设驾驶员有两个停车场可供选择,为了表示驾驶员在不能区分两种停车场的成本大小时选择停车的偏好程度,本文提出一个表征出行者选择偏好的参数τ. (3) 式中:P1为驾驶员选择停车场1的可能性;U1、U2分别为停车场1和停车场2的感知成本;Δ(无差异阈值)为驾驶员可以区分两个停车场成本的范围,且Δ≥0,当效用差大于Δ时,出行者可以做出理性决策,选择停车场1;当效用差小于Δ时,驾驶员根据P1做出选择.τ为选择偏好系数,当τ=1时出行者完全偏好于第1个停车场;当τ=0时出行者完全偏好于第2个停车场;当τ越接近1时,驾驶员选择停车场1的概率越大.若τ=0.5时驾驶员对停车场选择无偏好,随机选择停车场. 联立式(2)~(3)得出驾驶员选择停车场1的概率P1为 P1=Pr(U1-U2>Δ)×1+ Pr(-Δ Pr(V1+ε1-V2-ε2>Δ)×1+ Pr(-Δ Pr(ε2-ε1<-Δ-V2+V1)+Pr(V2-V1-Δ< ε2-ε1 (4) 由式(4)得到的是只有两个备选停车场时选择停车场1的概率,将其拓展到有m个备选停车场时,选择停车场1的概率,具体见定理1. 定理1当有m个停车场时(m≥2),可以得到驾驶员选则停车场1的概率P1为 (5) 证明当停车场数量为m时(m≥2),将选择概率分为如下m个部分,计算出每个部分满足的概率再相加可得选择停车场1的概率. 1) 停车场1的效用与其他停车场的效用差均大于Δ. (6) 2) 停车场1与某一个停车场的效用差小于Δ. (7) 3) 停车场1与某二个停车场的效用差小于Δ. (8) …… 4) 停车场1与其他停车场的效用差均小于Δ. (9) 式中:τ1i为停车场1相对于停车场i的偏好程度;τ1…m为面对m个停车场时,对停车场1 的偏好程度,若无偏好τ1…m=1/m. 选择停车场1 的概率P1=P10+P11+P12+…+P1(m-1),定理1即证. 通常出行者在选择停车场的时候会权衡路径行驶时间、燃油费、停车位与目的地的距离、停车费用等各项成本.由于模型中考虑的是费用差值,且出行者由当前位置到达各个备选停车场的距离相差不大,故其燃油费的差值可以忽略不计.故出行者的感知固定成本Vi为 (10) (11) 步行距离指的是出行者从停车场i,步行至目的地s的距离.步行时间Twalk为 (12) 式中:Lis为停车场i到目的地的距离;vwalk为出行者单位步行速度. 停车场收费情况指的是停车场i所执行的收费标准.车辆停车费CP为 CP=fi×t (13) 式中:fi为单位时间停车费率;t为停车时长. 则出行者的感知成本Ui. (14) 式中:Vi为感知成本的固定项;εi为感知成本的随机项,服从参数为(0,θ)的二重指数分布. 表1 停车场相关信息 表2 路段参数值 定理2当停车场的空余泊位得到均衡利用时,即泊位均衡指数差值取得最小值,停车费率差值为 (15) 式中: (16) 为了便于计算,令K=H2M1-H1M2+H1Q、H=H1+H2,则 (17) (18) (19) (20) (21) 则V2-V1=lnG-Δ,通过计算即可得到式(15),定理2即证. 令τ=0.5,即驾驶员对两个停车场的选择无偏好,在不能区分各自效用大小时随机选择,此时绘制无差异阈值Δ与选择停车场1概率P1关系见图2. 图2 τ=0.5时停车场1选择概率与Δ关系 由图2可知: 1) 当Δ=0时,即驾驶员基于完全理性选择停车场,当V2-V1=0的差值越大,驾驶员选择停车场1的概率越小,即驾驶员会选择效用最大的停车场;当Δ≠0时,即驾驶员是在有限理性下选择停车场,概率曲线在V2-V1=0的附近比较平缓,且随着差值的增大,其平缓度会逐渐降低. 2) Δ越大,概率曲线在V2-V1=0附近越平缓,说明无差异阈值Δ 越大(理性程度越低),驾驶员对停车场之间效用的微小差距敏感度越低,当Δ趋于无穷大的时候,驾驶员对于效用差值完全不敏感,驾驶员随机选择停车场,故其图像无限接近与y=0.5. 令Δ=4,绘制选择偏好系数τ与选择停车场1概率P1关系图见图3. 图3 Δ=4时停车场1选择概率与τ关系 由图3可知: 1)当效用差比较大的时候,几条曲线比较接近,当效用差在0附近的时候,曲线差别很大,表明驾驶员的偏好程度在停车场效用差不大的作用比较明显,这是因为在效用差比较小时(小于Δ),驾驶员无法做出理性判断,只能根据偏好程度选择. 2) 选择停车场1的概率P1与偏好系数τ呈正相关,当效用差一定时,概率P1随着偏好系数τ的增大而增大、 本文公式中的参数取值见表3,根据式(15)及表1、2相关信息,求得在泊位空闲指数差异均值最小的时候,停车费率的差值与停车时长应满足的关系图. 表3 参数取值 令τ=0.5,绘制无差异阈值Δ与停车费率差值关系图见图4.由图4可知:当停车时间减少时,停车费率的差值应该增大以达到泊位空闲指数差异均值减小,进而达到空闲泊位的均衡利用;当驾驶员的无差异阈值Δ增大时,停车费率的差值应该增大以达到泊位空闲指数差异均值减小,根据上文的分析无差异阈值Δ 越大(理性程度越低),驾驶员对停车场效用的微小差距敏感度越低,所以当Δ增大时,停车费率的差值应该增大. 图4 τ=0.5时停车费率差值与停车时长关系 令Δ=4,绘制选择偏好系数τ与停车费率差值关系图见图5.由图5可知:为了达到空闲泊位的均衡利用,当停车时间减少时,停车费率的差值应该增大,停车费率差值的变化对偏好系数τ的敏感性较低. 图5 Δ=4时停车费率差值与停车时长关系 1) 无差异阈值Δ越大(理性程度越低),驾驶员对效用差距敏感度越低;当阈值大于效用差时,驾驶员随机选择停车场,当阈值小于费用差时,驾驶员选择效用最大的停车场. 2) 选择停车场的概率与偏好系数τ呈正相关,且当停车场效用差越小,驾驶员的偏好程度对选择的影响越大. 3) 通过对停车费率的调整,影响驾驶员停车场选择可以达到泊位的均衡利用,费率的调整受到停车时长的影响,停车时长越短,费率差值应越大. 本文分析停车费率差值与停车时长的关系时,无差异阈值Δ与偏好系数τ均是假设值,且假设所有驾驶员的Δ、τ相等,即只考虑了一类社会群体有限理性下的行为特征,需要通过数据分析确定不同社会群体无差异阈值Δ与偏好系数τ,扩充研究对象,改进模型.本文只研究了当前位置到停车场的走行时间、停车费用以及步行时间等因素,只考虑了目的地附近两个备选停车场的泊位均衡,后续研究可以基于多群体、多因素、多停车场建立模型,实现区域内的泊位均衡.1.3 出行者感知固定成本



1.4 泊位均衡分析




2 模型分析
2.1 选择停车场1的概率P1与Δ、τ关系分析


2.2 停车场费率差值与Δ、τ关系分析


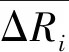
3 结 论

