基于高校四级成绩数据的重采样方法研究＊

夏 艳，张丽娟

(广州华商学院，广东 广州 511399)

0 引言

大学英语等级考试一直以来都是高校学生参与度最高的全国性考试，其考试成绩不仅反映了学生的英语学习能力，其证书也是高校毕业生求职应聘中所必备的。

评估高校各专业整体英语应试水平，对于高校管理层在专业层面上提出相关英语教学改革措施极为重要。Bootstrap 与Jackknife 是抽样调查中常用的重采样方法，Jackknife 是由Quenouille[1,2]（1949/1956）作为减少系列相关系数估计量偏倚的一种方法提出的，后来逐渐成为复杂样本方差估计的一种重要方法。Bootstrap 是由B.Efron[3](1979)在Jackknife 的基础上提出的一种利用重抽样方法对总体参数进行估计的统计方法。吕萍[4]（2017）指出在数据分析中,若忽视层、群等抽样设计的复杂性,直接利用调查数据按照传统数据分析方法,容易得出错误的结论,尤其是涉及标准误的估计。Bootstrap 方法的优势在于对小样本进行评估时,可极大地降低评估样本不足对评估结果的影响[5]。该方法也在估计中存在些许不足，主要体现在重抽样都是在已知的样本观测数据中进行的，这使得自主样本与原样本的相似度较高，并且样本量越小，其相似度就越高，估计结果与真实分布的差异性也会越大[6]。Jackknife 方法在方差分量估计和标准误估计上都较为准确，且其估计的准确性不随数据类型、研究设计和方差分量的不同而产生波动，具有较强的稳健性[7]。Jackknife 方法不足之处主要体现在：估计总体统计量时只利用了很少的信息，各采样样本之间的差异很小，每两个Jackknife 样本中只有两个单一的观测值不同。本文在估计总体样本均值的过程中，考虑到Jackknife 算法与Bootstrap 算法存在的不足，提出Bootstrap-Jackknife 算法，得到了更接近于总体样本均值的估计值。

1 数据与估计方法

1.1 数据来源与处理

本文采集广州华商学院各专业学生在2017 学年的四级成绩数据，共计9860 条有效数据，并对收集的数据进行对数化处理，数据对数化可以使得样本数据更加光滑，消除异方差,同时减小数据波动范围。

1.2 Normal

将采集得到的观测样本x1,…,xn当做总体样本的近似，通过观测样本得到各样本统计量值以估计总体统计量，其中总体标准差的无偏估计如式⑴：

1.3 Bootstrap

Bootstrap 是一种著名的方差估计方法，其思想是通过重复抽样来估计总体分布。具体来说就是将得到的样本Fn(x)当做总体F(x)的近似是θ的一个估计，通过从得到的样本中重复有放回抽样生成经验累积分布函数(x)，对生成的(x)样本进行相应计算得到，利用一系列实现的置信区间评定。具体步骤如下：

⑴从观测样本x1,…,xn中有放回地抽样生成样本

⑵对第b个Bootstrap 样本计算估计值(b)，这里b的范围为1-2000，本文为了使全部的数据尽可能被采集，使得总体统计量的估计结果更为稳健，规定抽样次数B=2000；

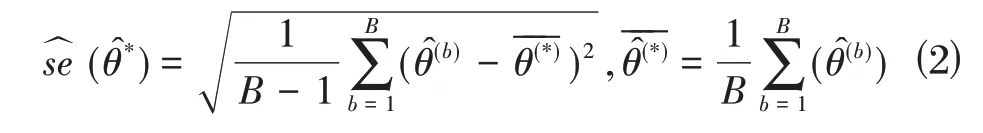
1.4 Jackknife

Jackknife 可用于总体估计量的不确定估计，旨在减少估计的偏差。其思想为“去一”抽样，假设获取样本样本量为n，在第i次抽样中去除第i个样本数据i=(1,2,...,n)，用剩下的(n-1)个数据作为抽样样本计算，分别对生成的n个样本计算相应的样本统计量，如此得到，从而实现总体统计量的置信区间估计。具体步骤如下：

⑴ 从观测样本x1,…,xn中做i次Jackknife 抽样，生成第i个Jackknife样本(x1,…,xi-1,xi+1,…,xn)；

⑵对n个Jackknife样本计算估计值

⑶当利用Jackknife对θ进行标准差估计时，如式⑶：

1.5 Bootstrap-Jackknife

在实际应用中，Bootstrap 对估计量的相关估计值具有随机性，即每一次运用Bootstrap 算法抽样得到的估计值并不相同，而使用Jackknife 对统计量进行估计时，各采样的样本之间的差异太小。本文考虑到Bootstrap 与Jackknife 的不足之处，结合两种算法，创新性地进行相关方差估计。采用Bootstrap 选取多组样本，随后采用Jackknife 对每组样本分别进行均值与标准差的估计，结合实际训练数据发现该方法得到的估计值稳健度更高。本文实现Bootstrap-Jackknife 的具体步骤如下：

⑴ 对于观测样本x1,…,xn，进 行B=2000 次Bootstrap抽样，每次抽样n个样本；

⑵假设i=1:n，每次选取上一步所有Bootstrap样本中不含有xi的样本，并重新计算θj(i)；

⑶对第j个Bootstrap 样本生成的所有θj(i)计算相关估计值与标准差，标准差如式⑷：

2 实例分析

分别采用Normal、Bootstrap、Jackknife、Bootstrap-Jackknife 方法，对实际样本数据进行均值估计，实际训练样本为该校各专业学生在2017 学年的四级成绩对数。估计结果对比情况如图1所示。

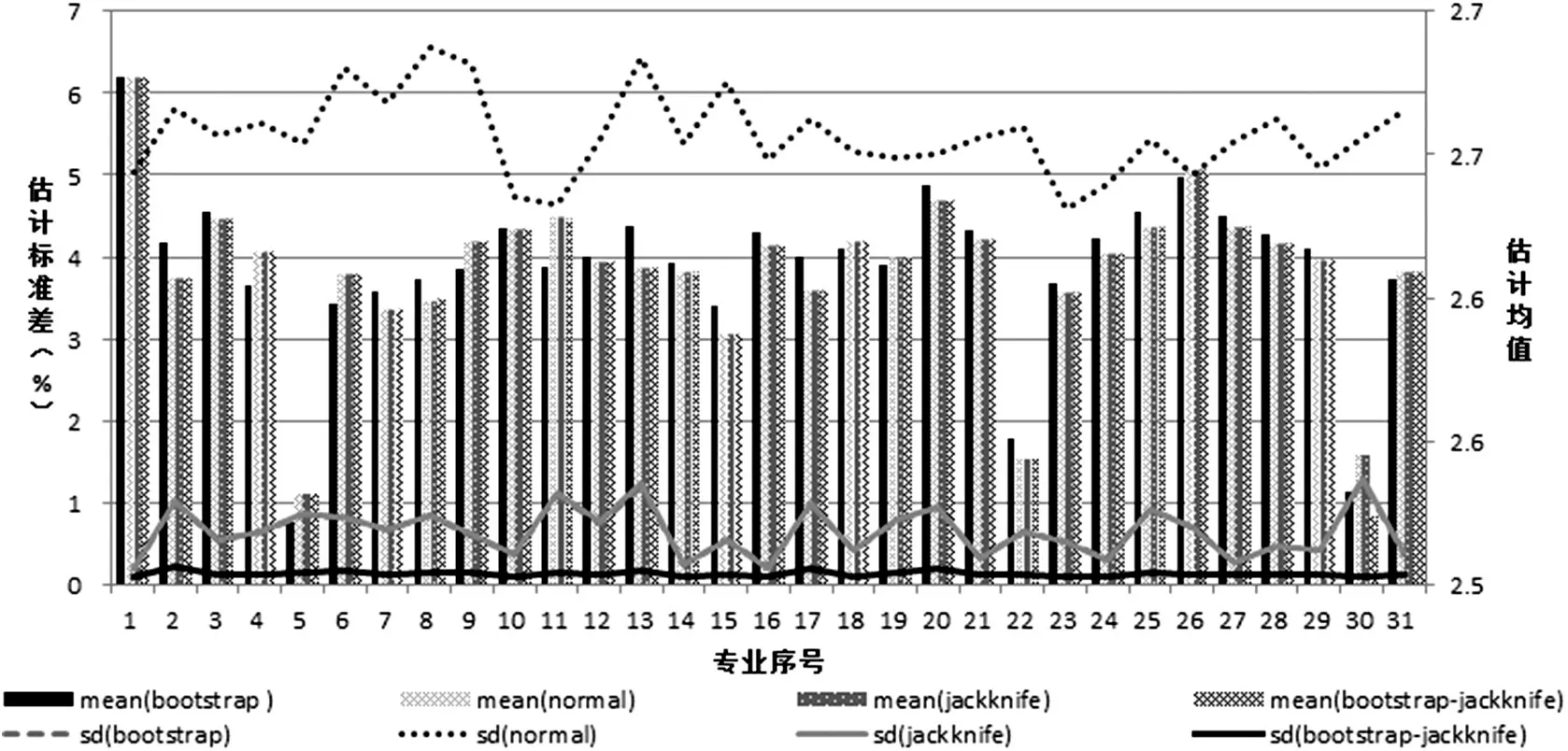
图1 四种方法估计在实际数据上的效果对比图

由图1数据可以看出：①对于Normal、Jackknife 与Bootstrap-Jackknife 这三种方法计算出的均值估计量仅有细微差异，而Bootstrap 得到的均值估计值与其他三种方法得到的均值估计值相差较大；②对于标准差估计，Bootstrap-Jackknife 估计得到的标准差要远远小于其他三种方法估计的标准差，这说明在对总体均值的估计中，Bootstrap-Jackknife 的估计误差最小，即利用该方法得到的均值用来估计总体均值，其精度最高。另外Bootstrap与Jackknife的标准差估计值几乎重合为一条折线且远小于普通法的标准差估计值，这说明利用Bootstrap 与Jackknife 对估计量进行估计，其可信度要高于普通法得到的估计量值。

为了更明显的显示四种方法估计样本均值的差异，本文将四种方法得到的样本数据均值估计值进行排序，具体排序结果如表1所示(仅列举部分)。

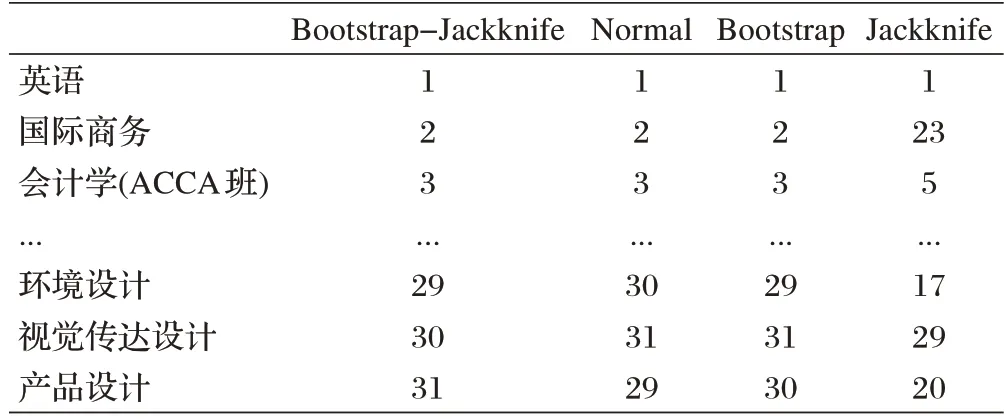
表1 四种方法估计的均值排序对比

为比较Bootstrap-Jackknife 方法与其他三种方法排序结果之间的差异，本文将各专业Bootstrap-Jackknife排序结果与其他三种方法得到的排序结果做差值处理，并进行绝对值运算，依据各差值结果绘制箱线图，如图2所示。

图2 各专业排序差绝对值箱线图

结合表1 排序数据与图2 箱线图可以看出：第一，Normal 与Bootstrap-Jackknife 在专业排序上的差异甚微，Bootstrap-Jackknife与Jackknife在专业排序上的差异最为显著，这说明就均值估计而言，Jackknife估计的稳定性并不高；第二，就排序数据上来看，该校英语四级应试能力前三的专业为英语、国际商务和会计学（ACCA 班），而英语四级应试能力较差的专业为环境设计、视觉传达设计、产品设计这三个艺术专业。

3 结论

本文基于广州华商学院2017 学年各专业学生四级成绩数据，运用Normal、Bootstrap、Jackknife 和Bootstrap-Jackknife 四种方差估计方法分别评估该校各专业四级总体应试水平；对比估计结果发现：Bootstrap-Jackknife 算法在估计总体均值方面上估计误差最低，在涉及排序问题上，Jackknife算法的排序稳定性最低。研究结果表明，Bootstrap-Jackknife算法可更精确、稳定的评估高校各专业总体英语应试水平，从而为高校在专业层面上制定科学的英语学习方式和可操作的实施办法[8]提供参考。