阶次跟踪与改进小波阈值降噪的RV 减速器故障诊断

蔺梦雄 王 爽 韦克吉 张向慧 曹洪鑫 张敬彩

（①北方工业大学机械与材料工程学院，北京 100144；②中机生产力促进中心有限公司，北京 100044）

RV 减速器作为工业机器人的核心零部件[1]，在机器人领域和高精密机械领域中有着广泛的应用。随着国家工业制造2025 计划的提出，我国科学家以及企业单位对RV 减速器的研究在逐步加深，尤其对减速器的可靠性要求更加严格，所以在机器人用RV 减速器的故障诊断方面受到行业内和学术界越来越多的关注。RV 减速器组成复杂，零部件多，根据RV 减速器的工作特点，在实际工作中减速器齿轮的啮合和轴承的传动循环受到变速和重载的冲击，使得减速器内部零部件极易受损。轻则损失精度，重则造成疲劳失效。然而减速器的非计划停机会导致实验、测试中断从而带来极大的损失，所以做好RV 减速器工作时的状态监测及故障诊断预测具有十分重要的意义。

RV 减速器内部构造复杂，在振动信号采集过程中必定掺杂着噪声等不必要的影响，利用小波分析理论和噪声干扰下的卷积神经网络模型（ANNet）算法对振动信号进行处理分析，可以比较准确地对RV 减速器的故障磨损进行诊断[2-3]。李先锋等[4]通过模拟实际工况进行试验，提取不同故障类型的特征数据并整理，利用Visual Studio 软件建立RV减速器轴承故障诊断系统，提高轴承故障类型的识别率以及故障位置、程度的诊断精度。Sun Y G[5]提出了复信号的小波去噪方法，对RV 减速器进行了故障诊断。建立故障树并且用蒙特卡罗法进行仿真，验证了该方法的有效性。汪久根等[6]利用采集到的4 种故障下和正常的RV 减速器振动信号，通过残差网络分析方法与DNN、LeNet、10 层CNN等模型分析方法进行对比，结果表明残差网络的故障分辨率更高。Zhi H[7]采用一种远程控制诊断方法，通过对RV 减速器工作时的振动信号进行分析和特征提取，并利用灰色马尔可夫模型进行分析和预测，提高了RV 减速器故障诊断率。Peng P[8]通过建立噪声深度卷积神经网络模型（NOSCNN），可以在RV 减速器变工况进行故障识别，并提高了分析模型抗的干扰能力，通过实验数据分析对比，证明了该方法更具有稳定性。陈乐瑞等[9-10]提出了一种基于非线性输出频响函数(NOFRFs)和深度卷积神经网络(CNN)的RV 减速器故障诊断新方法。解决了输出信号不能描述系统非线性特性导致的精度不高的问题。并提出了一种自适应的网络结构优化算法，通过实验验证了该方法的可行性，提高了RV减速器的故障诊断率；此外，提出了一种基于非线性输出频率响应函数频谱与核主元分析(KPCA)相结合的方法诊断RV 减速器故障，实现了对RV 减速器5 种故障的诊断，有效地提高了诊断精度。

上述学者对行星摆线针轮减速器的监测方法大多是在减速器匀速工作状态下进行分析诊断的，或者是利用较为复杂的算法和高精密的设备进行分析，分析成本和计算要求都比较高。而在RV 减速器主要应用在机器人的轴关节处，在其实际工作中，由于运行工况和要求的不同可能导致转速和负载随时在变化，其振动信号呈现明显的非平稳性。传统的频谱分析在时变工况下的分析会造成频率模糊现象，无法准确地进行诊断和监测。

阶次跟踪分析是一种应用于变转速的旋转机械故障诊断分析方法，能够解决传统的频谱分析在变转速工况下分析中出现的“频率模糊”现象。田家彬[11]建立了风力发电机齿轮箱的振动信号模型，对采集的振动信号进行阶次跟踪分析，准确定位了风力发电机齿轮箱的故障点。毛清华[12]利用阶次跟踪分析与包络谱相结合的方法，对变工况下的采煤机齿轮传动系统进行了准确的故障诊断。王博等[13]利用阶次跟踪分析成功地提取了非平稳工况下的行星齿轮箱的故障特征。冯刚等[14]利用改进COT 算法与阶次跟踪分析结合，提高了阶次跟踪分析的精度；再结合自适应变分模态分解法成功地对齿轮箱的进行了故障识别。

小波阈值降噪法包括软阈值降噪和硬阈值降噪两种，广泛应用于旋转机械的故障诊断中，但是该方法本身存在一定缺陷，小波硬阈值函数不连续，降噪后会产生震荡，软阈值降噪连续性稳定，但是处理后的小波系数和真实小波系数存在误差，导致重构后的信号精度下降。因此，本文基于一种改进的小波阈值降噪方法[15]，结合阶次跟踪分析，对RV 减速器进行了故障诊断。由于RV 减速器内部结构复杂，噪声较多，诊断起来非常复杂，首先利用改进小波阈值降噪对其进行降噪处理，再通过阶次跟踪分析对RV 减速器的故障点进行定位，通过处理对比和分析验证，传统的小波降噪分析结果在低阶次处理并不明显，而改进小波阈值降噪的结果更为直观。通过对RV 减速器拆机验证，证明了该方法的可行性。

1 RV 减速器工作原理

RV 减速器的简化传动示意图如图1 所示，中心齿轮1 为输入轴，与行星轮2 连接，带动行星轮转动，行星轮和曲柄轴3 相固连，利用两个曲柄轴使摆线轮6 产生偏心运动，通过摆线轮与摆线针轮5 啮合，使得行星架7 作为输出传动。

图1 行星摆线针轮减速器传动简图

2 阶次跟踪分析与改进小波阈值降噪方法

2.1 阶次跟踪分析

阶次跟踪分析方法的主要思想是通过信号处理算法，将等时域间隔的振动数据采样转换到角度域的等角度采样，再通过对等角度域信号做快速傅里叶变换（FFT）即可得到阶次图。由于大多数的旋转机械都是在非平稳的工况下进行工作，阶次分析成为了许多分析方法中的首选[16]。在分析过程中，选择某一轴作为参考轴，以其转频作为基准，相对于基频的倍数称为阶次。

阶次、频率与转速之间的关系为

式中：O为所监查对象的阶次；f为所监查对象的频率；v为参考轴的转速。

2.2 改进小波阈值降噪

当采用小波阈值降噪方法的关键在于阈值和阈值函数的选取。不同的阈值函数会直接影响到降噪的效果，只有选取合理的阈值时，才能得到正确的结果并且保证关键信息不会丢失。传统的小波阈值为小波硬阈值函数和软阈值函数，其表达式为

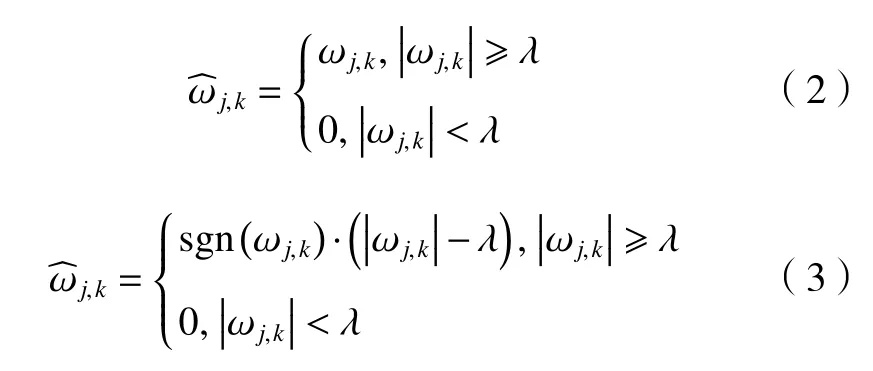
硬阈值和软阈值虽然在实际中得以广泛地应用，但这些方法本身还存在一些缺陷，如会出现不连续的间断点和信号失真等问题。为了克服小波软、硬阈值方法的缺点，本文利用一种改进小波阈值函数的选取办法来弥补传统小波阈值的不足，新改进小波阈值表达式为

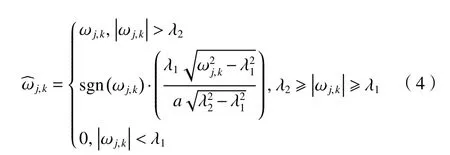
式中：λ1和λ2为阈值，且 λ1=aλ2(0 ＜a≤1)，此阈值函数在小波域内具有连续性，解决了间断点及信号失真的问题，通过选取适当的a调 节参数的值得到合适且有效的阈值函数。λ1由下式计算得到。

式中：M表示信号长度；σ表示第k层噪声的标准差，按下式估算，得

本文利用改进小波阈值降噪与阶次跟踪分析相结合的方法对RV 减速器进行故障诊断分析的方法如下：

（1）对采集到的RV 减速器的振动信号进行角域重采样，得到减速器的等角域振动信号。

（2）利用改进小波阈值降噪法对等角域振动信号进行降噪重构，得到小波硬阈值分解信号、小波软阈值分解信号和新小波阈值信号波形图。

（3）计算出3 种降噪方法的信噪比和均方根误差值。

（4）选取最优降噪信号对其进行等角域划分，对得到的等角域信号进行快速傅里叶变换得到阶次图。

（5）通过与减速器的理论故障阶次进行对比，确定故障点。

3 RV 减速器的故障特征阶次

本文以一款RV 减速器为例，假设输入轴作为输入端，中心齿轮齿数为12；行星齿轮齿数为36；摆线轮齿数为39；针轮齿数为40。曲拐轴承的轴承节径为33 mm，滚动体直径为5 mm，接触角为0°，滚动体个数为 14。主轴承的轴承节径为130 mm，滚动体直径为8 mm，接触角为34°，滚动体个数为 36。

根据行星摆线针轮减速器的工作特点，对RV减速器的主要零部件进行特征阶次计算[17]。以中心齿轮为输入端时，各零部件故障特征阶次如下表1所示。

表1 RV 减速器各零部件故障阶次

确定好参考轴和各零部件的故障阶次后，通过分析采集RV 减速器正常情况和故障情况下工作时的振动信号阶次图，参考表1 中各零部件的故障特征阶次对比能量峰值变化情况，就可以准确地确定减速器的故障点。

4 故障信号分析

为了还原RV 减速器的真实工作状态，本文选择RV 减速器进行单摆疲劳实验的工况下，采集到的振动信号利用本文提出的方法进行研究。本实分析对象为RV 减速器两个摆动周期时所采集的数据。分析信号的振动时域信号，如图2 所示；对其进行角域重采样得到等角域振动信号图，如图3 所示。将等角域振动信号进行改进小波阈值降噪分析，得到硬阈值降噪、软阈值降噪和新小波阈值降噪结果，分别如图4～6 所示。计算这3 种小波阈值降噪方法的信噪比和均方根误差，结果如表2 所示。

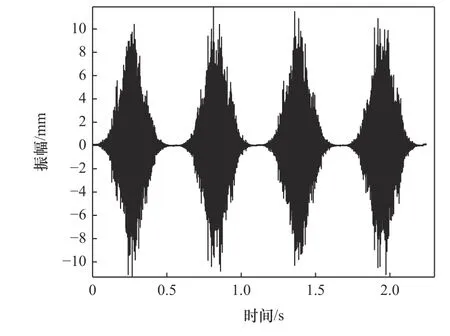
图2 RV 减速器故障下时域波形图

图3 减速器故障情况下等角域振动信号图

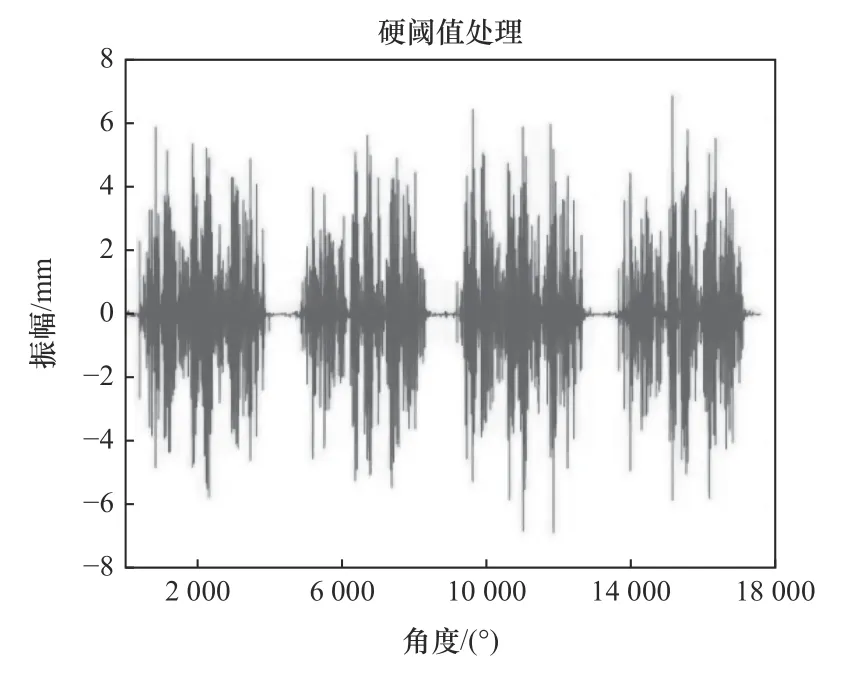
图4 小波硬阈值处理结果

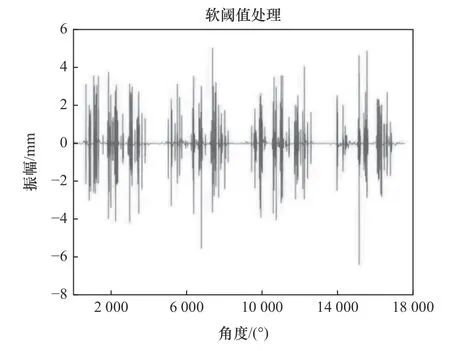
图5 小波软阈值处理结果

利用改进小波降噪后的图像可以看出，降噪效果明显；由图4～6 可以明显对比看出，改进阈值降噪处理的效果优于其他两种方法，并且能看比较明显的、规律的故障冲击特征。由表2 可以看出，改进阈值降噪分析的信噪比和均方根误差都优于其他两种阈值降噪方法，体现了改进阈值降噪的优越性。

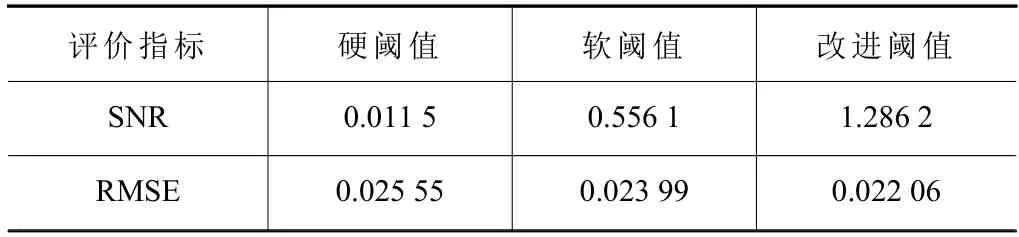
表2 行星摆线针轮减速器故障信号的3 种阈值函数的降噪评价指标

对改进阈值处理后的等角域图进行快速傅里叶变换，得到改进小波阈值降噪处理后的阶次图，如图7 所示；通过前面对行星摆线针轮减速器的故障特征阶次的计算，和减速器的滚针部位的特征阶次相吻合，能够断定减速器的滚针部位发生磨损，验证了此方法的可行性。

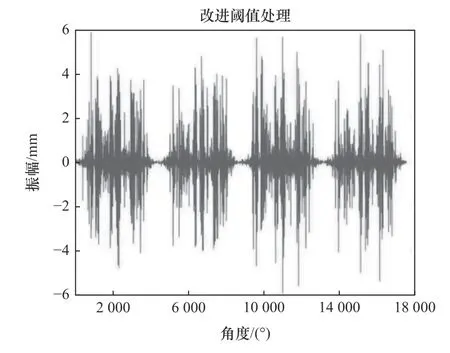
图6 小波改进阈值处理结果

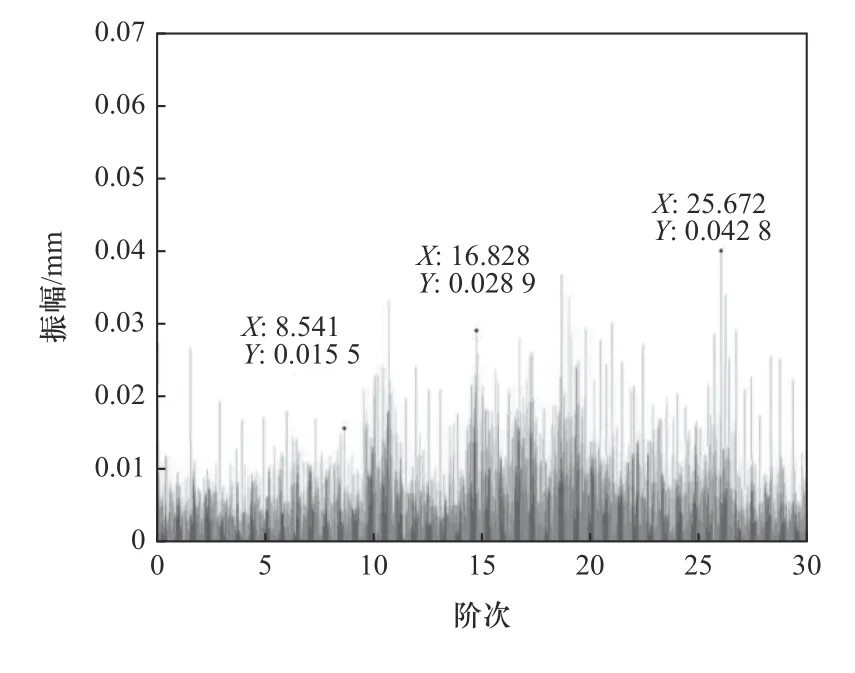
图7 故障情况下振动信号阶次谱图

5 阶次跟踪结合传统小波降噪分析

为了验证改进小波阈值方法的优化性，本文选用传统小波降噪结合阶次跟踪分析与之做对比实验。通过对图3 等角域图进行传统小波降噪重构，得到降噪后的等角域图，如图8 所示。通过对传统小波降噪的结果进行阶次分析得到图9。从图9 中可以看出，在分析振动信号的低阶并无明显阶次能量峰值，而在高阶中可以对应出减速器滚针的故障特征阶次分布。

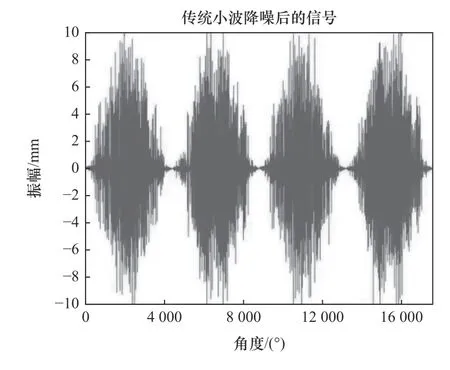
图8 传统小波降噪后的等角域信号

图9 传统小波降噪后的阶次分析图

6 实验验证

在进行完单摆疲劳实验后，去掉摆臂，利用匀转速实验对实验结果进行验证。减速器输出端设置为15 r/min，采集信号设备同上。图为减速器在正常情况下的阶次跟踪分析图，从图10 和图11 对比看出，减速器在故障情况下，在8.341、16.52 和25.06 阶处有明显峰值，基本符合预设滚针故障特征阶次的倍频，和疲劳实验下阶次分析的结果非常接近，可以很好地和疲劳实验结果验证。

图10 正常匀速下振动信号阶次图

图11 故障状态下匀速振动信号阶次图

随后拆开减速器进行结果验证。找到对应零部件后，发现减速器的摆线轮隔套发生断裂状况，减速器工作过程中，隔套断裂处与滚针接触，导致滚针出现较严重磨损。减速器滚针故障如图12 所示。通过拆机验证，证明了该方法的可行性，相对传统小波降噪的分析结果，改进小波阈值降噪方法的结果有极大的优越性。

图12 减速器摆线轮隔套以及滚针磨损、隔套断裂图

7 结语

利用改进小波阈值降噪和阶次跟踪分析结合的方法，对RV 减速器摆动疲劳实验中所采集到的振动信号进行等角域转化、改进小波阈值降噪、快速傅里叶变换得到阶次图；对比故障前后的阶次能量峰值，可以准确定位减速器的滚针部位发生磨损。结果表明，对等角域图进行传统的小波降噪后，得到阶次图在滚针的低阶不能找到明显的故障特征阶次；利用改进阈值小波降噪后进行阶次分析可以在低阶找到对应故障点。证明该方法在RV 减速器的故障诊断中行之有效。