基于SIS模型的电网扰动预测与分析方法

闫 静，刘 凯

（1.国网江苏省电力有限公司超高压分公司，江苏 南京 211100；2.国网江苏电力有限公司扬州市江都区供电公司，江苏 扬州 225200）

0 引 言

随着电网互联节点数量和电网负荷的不断增加，电动汽车不断接入电网，新能源的不断大规模整合，电力市场不断改革，这些日益增长的因素的影响继续扩大,电力系统的随机性日益影响着电力系统的安全稳定，因此保证电网安全运行变得至关重要，其中电网扰动是影响电网安全的重要原因之一[1-3]。电网扰动的扩大化是随着电力设备的运行参数剧烈变化所产生的，对扰动进行分析，找出其传播规律，通过分析电网扰动的传播规律，可以提前采取相应的对策，大大降低电网扰动对电网的影响，从而保证电力系统安全稳定运行[4]。

在传统的电力系统动力学领域，主要研究的是确定性模型，它没有考虑系统的随机因素对电力系统的影响，传统方案在很大程度上依赖于确定性模型，并且在建模的过程中对建模的简化和假设使得建模分析得到的结论不能准确地与实际存在的问题相对应，有较为明显的局限性[5-7]。在建模过程中，没有采用假设来预测系统未来的问题，在很大程度上无法准确、真实地反映电力系统稳定运行的隐患。电力系统通过数据分析对电网扰动传播进行深入研究缺乏合适的理论基础[8]。

因此，构建一个完善的随机电网扰动传播模型可以对电网扰动有更直观、更准确的认识。本文通过将生物学领域中完善的SIS模型与电网扰动传播相结合，运用SIS模型预测传染病传播蔓延的方法，在电网扰动传播的时间去预测电网扰动的程度，提前对电网扰动影响进行预警，这样及时有效且准确地制定出针对方案对电网运行进行宏观调控，从而降低电网扰动传播对电网及电力系统造成的影响，使得电网更加安全稳定的运行。

1 传染病模型

生物学很早就开始了对传染病的研究，在建立传染病模型研究的基础上，进而推广了传染病的动力学模型，生物学家也建立了比较完整和应用广泛的传播模型[9,10]。传染病动力学是一种重要的理论定量研究方法。根据人口的特点、疾病在人口中的传播和发展等因素，建立了能反映传染病动态的数学模型。

通过对该模型的定性分析和数值模拟，可以分析其发展过程，揭示其流动规律，预测其变化趋势[11,12]。传染病基本数学模型通过研究疾病的传播速度、空间范围、传播路径、动力机制等问题，及时预测传播趋势，可以有效地预防和控制疾病的传播。感染率与痊愈率的比率被用来衡量传染病的强度。在节点上，感染率为健康节点被感染节点感染的比例。感染率越大，被感染的健康节点增长就越快。

传染病模型历史悠久，主要包括SI模型、SIS模型、SEIR模型和SEIRS模型[13,14]。SIS模型是传染病模型中最经典的模型之一，如图1所示。

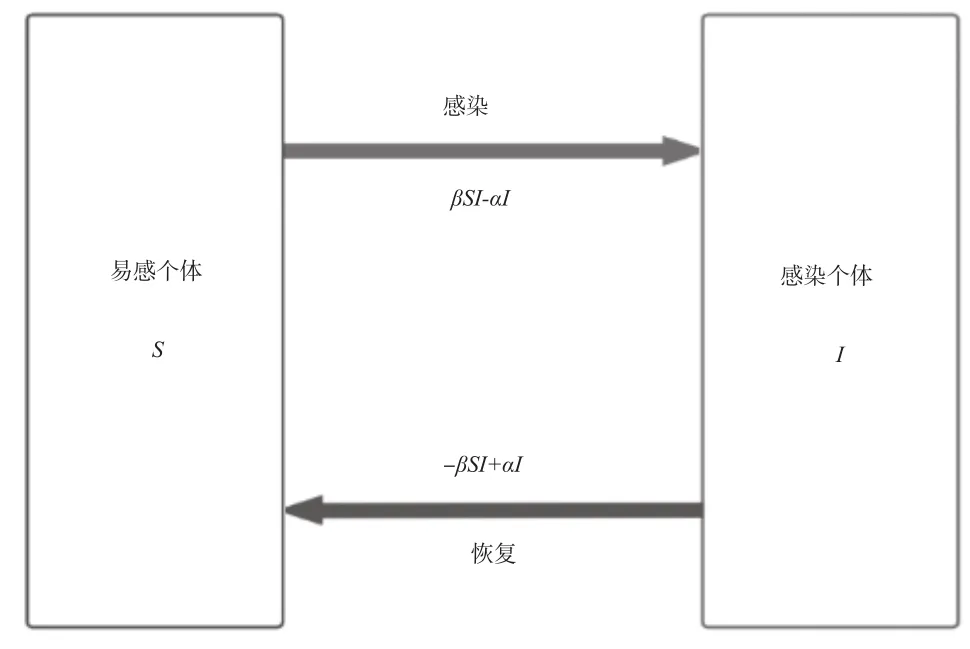
图1 SIS模型个体数量变化

在SIS模型下，将总体人群分为易感人群和受感人群。设S为易感个体的数量，I为感染个体的数量，感染率为β，治愈率为α，并假设感染个体恢复后未产生免疫力。

在传染病暴发的初始阶段，总群体中的某个或者几个个体受到了感染，将通过某种概率传染给周围的其他个体。假设S类个体受到感染，这些个体将变成I类个体，成为了新的感染源，然后继续往周围扩散，这个传播过程与电网中的故障极其类似。

在该模型中存在下列几种假设条件：（1）在整个群体中，每个个体的免疫能力较为脆弱，一旦受到感染源接触，则会变成感染者，成为新的感染源；（2）被感染者可以接受治疗成为易感染者；（3）假设该群体总人数不变，对新出生及死亡的人口忽略不计；（4）不考虑病毒的变异。

因此在SIS模型中，一个感染个体在单位时间内与βN个个体接触，其中被接触过个体是易感个体的可能性是S/N。因此，单位时间内被感染个体数为

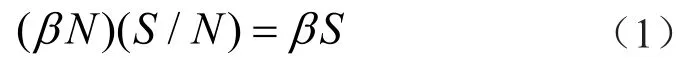
I个感染个体单位时间内造成βSI个体被感染，并且单位时间内有αI个感染个体恢复，由此可得SIS模型为

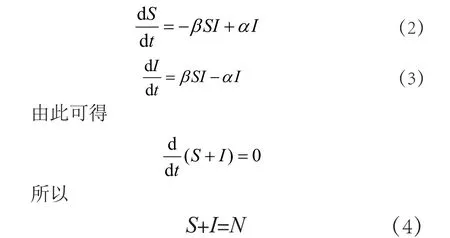
式中：N为常数，说明传播过程中总量不变。

2 扰动传播模型

在研究电网扰动的传播时，电网中的节点都有一定几率在电网扰动的影响下会成为新的扰动源，并逐渐向受影响的关键节点扩散[15]。在SIS模型中，个体感染，然后以一定的概率向周围的个体扩散。这些健康的个体一旦被感染，成为被感染的个体，就会成为新的传染源，再次传播，相当于电网发生连锁事故。由此扰动传播模型和传染病模型可进行对比，如图2所示。

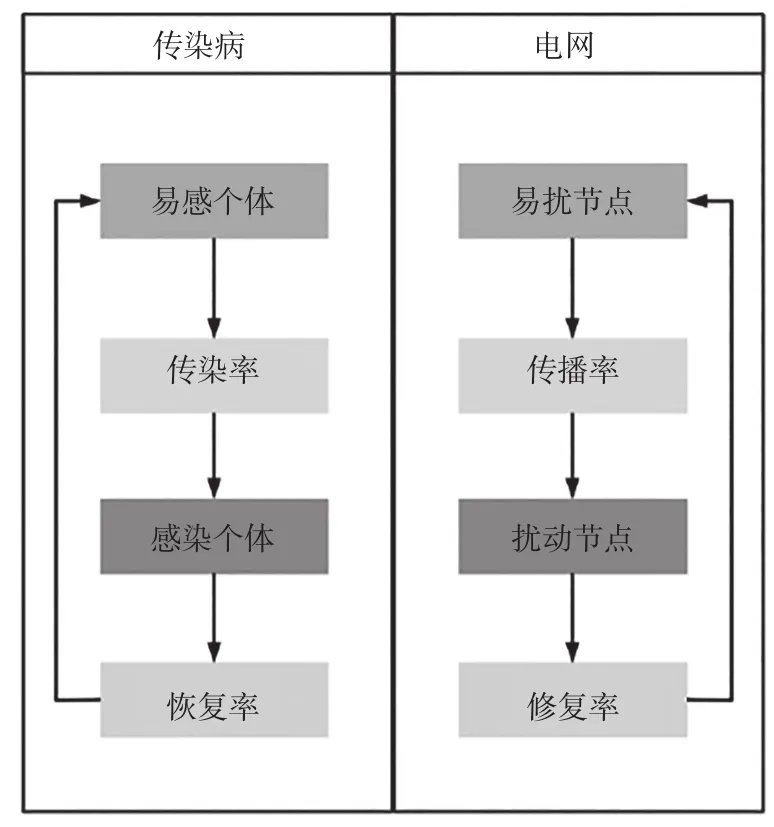
图2 扰动传播模型和传染病模型流程对比

通过分析其运动特征，预测扰动传播，并在其造成重大事故之前，切断扰动源以防止其大面积蔓延。在建立新的电网扰动传播模型时，电网模型有2个假设：（1）所有节点都相对脆弱，没有免疫扰动能力；（2）系统中的节点总数不变。基于SIS模型的基本思想，建立了电网扰动传播模型。将电网中各个节点状态分为S和I两种，设S为易扰个体的数量，I为扰动个体的数量，传播率为β，恢复率为α。由此电网和传染病模型参数可进行对比，如表1所示。

表1 扰动传播模型和传染病模型参数对比

将基本生殖数定义为

再将I=N-S代入式（3）得到

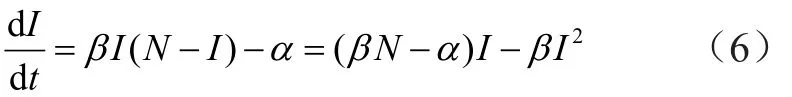
通过解dI/dt=0，可以得到SIS模型的2个均衡条件：（1）R0＜1且I=0时平衡：（2）R0＞1且I=N-α/β时平衡。

3 仿真分析

为了验证本文模型的正确性，本文在IEEE33节点系统中注入功率扰动进行扰动传播仿真，并使用MATLAB软件对33节点注入电压幅值、有功功率和无功功率进行仿真。

在电网扰动传播研究中，电网中的薄弱环节在电网扰动的影响下会成为新的扰动源，并逐渐向受影响的关键节点扩散；这一过程与SIS模型相同，即易感个体被感染个体感染，成为新的感染个体，并继续向外感染，在传染病爆发后影响种群。在SIS模型中，我们需要预测传染病的传播，在电网扰动传播过程中，我们也需要预测其传播。通过仿真SIS模型的数学模型，计算扰动传播节点的数学模型，通过仿真得到R0＜1和R0＞1时的结果如图3所示。

由图3（a）可以看出R0＜1时，节点修复速度大于节点扰动速度，因此并无扰动节点增长。在SIS扰动传播模型中，易扰节点在初始阶段隐藏在节点组中，被扰动节点扰动后成为扰动节点，修复后恢复为易扰节点。从模型中可以看出，随着时间的推移，易扰动节点越来越少，扰动节点越来越多，并在I=N-α/β时平衡。在此过程中，初始阶段扰动节点少，因此影响的易扰节点少，扰动节点数量增长速度慢；中期阶段，扰动节点较多，且节点群作为扰动节点容易被扰动，因此扰动节点数量增长速度快；后期扰动节点数量增加，易感节点数量减少，因此扰动节点增长速度速度慢。

如图3所示，在扰动节点达到平衡点之前，如果不及时制定解决方案，随着扰动节点数量的增加，电网将发生大规模停电，影响电网的安全，也会对人们日常生活造成很大的损害。

图3 扰动传播模型节点数量变化

综上所述，减少电网扰动传播的方法为：（1）增加电源线维修人员，提高维修效率；（2）在电力系统中增加断路器保护；（3）对干扰源进行反向分析，在前期阶段进行扰动修复。

4 结 论

本文所提出的方案主要用于解决电网输电中出现的扰动问题。利用SIS模型预测传染病传播的方法是预测电网扰动传递时电网扰动的程度，并对电网扰动的影响进行预警，从而及时、有效、准确地制定有针对性的解决方案，减少电网扰动传播对电网和电力系统的影响，使电网更加安全稳定。本文将电网扰动模型与传染病模型相结合，对电网扰动修复具有一定的指导作用。