基于IPSO优化BP神经网络的输电线路覆冰厚度预测算法

宋羽

安徽理工大学电气与信息工程学院 安徽淮南 232001

输电线路的覆冰会引发断线、舞动等电力系统灾害，更严峻时可能会出现倒塔，进而引起大规模断电，危及电力系统的安全[1]。2008年冰灾后，更多的监测设备被应用到电力运行维护工作中，但是摄像探头容易被冰雪掩盖，所以会存在在线监测设备的稳定性不够的问题[2]。输电线路的覆冰厚度越厚，其所承受的荷载就越高[3]，可见，对输电线路覆冰厚度进行预测是必要的。

在输电线路覆冰预测中常用的有数学物理关系模型[4]和基于神经网络的智能算法[5]。数学物理模型需求较高精度的气象参数，实际应用中很难达成。基于人工神经网络的智能算法因其特有的优势被普遍应用在覆冰厚度预测领域。文献[6]利用BP神经网络，运用Levenberg-Marquardt训练法解决了收敛速度慢的问题,同时提高了预测精度，但BP神经网络对权值较敏感，人为选择初始权值和阈值易导致拟合结果陷入局部极值。文献[7]将PSO算法与支持向量机算法相结合进行覆冰厚度预测，实现了自动寻优，但PSO算法易陷入局部寻优中，直接影响算法性能，进而影响预测精度。

考虑到以上方法所存在的问题，本文给出了一种基于改进粒子群优化BP神经网络覆冰厚度预测算法，改进后的算法降低了易陷入局部最优的风险，明显提高了收敛速度，预测精度也得到了提升。

1 基于BP神经网络的覆冰厚度预测算法

BP神经网络由输入层、隐含层和输出层组成，层与层之间相互连接。本文设置的为一个隐含层的BP，该网络输入层设置5个节点，隐含层设5个节点，输出层1个节点，所选转移函数为Sigmoid函数。

尽管BP网络拥有不错的泛化能力和并行性，但是仍存在以下问题：(1)收敛速度慢；(2)局部极小值问题；(3)BP神经网络的权值阈值的取值目前暂且没有理论依据，只能根据经验来进行人为选取。

因此，需要引入优化算法对其的阈值和权值进行自动寻优，但由于传统的优化算法存在陷入局部寻优的风险，所以本文选择引入改进的粒子群算法对BP神经网络进行参数优化，构建了一种IPSO-BP覆冰厚度预测算法。

2 基于IPSO-BP神经网络的覆冰厚度预测算法

2.1 粒子群算法

粒子群(Particle Swarm Optimization，PSO)算法中每个粒子即解空间中的某个解，它依据自身的位移路径以及同伴的位移路径来调整自己的移动。每个粒子在移动中所到达的最佳区域，就是这个粒子寻找到的最优解，即个体极值(pbest)。种群所到达的最佳区域即是种群的最优解，即全局极值(gbest)。种群中的每个粒子都依据这两个极值进行自我更新，形成新的种群。为了评估粒子的优劣程度，还需要定义一个适应度函数，一般可用输出误差来定义。

将群体中的粒子记为i，粒子到达的最优位置记为pbest，粒子的速度用vi表示。以下为粒子i的速度和位置更新公式：

vi=wvi+c1+rand()(pbest[i]-xi)+c2rand()(gbest[i]-xi)

(1)

xi+1=xi+vi

(2)

其中c1、c2为学习因子，一般选取常数；rand()是[0，1]上的随机数，w为惯性权重(inertia weight)。

公式(1)包含了三个部分，一是粒子的惯性部分，表示的是前一个时刻粒子的速度；二是自我部分，表示粒子自身的速度；三是群体部分，表示粒子受其他粒子影响的速度。惯性速度、认知部分与社会部分共同决定了粒子的寻优能力。

粒子群优化算法在寻优过程中，如果一个粒子到达某个局部最优点，则其他粒子会很快向其所在的方位移动，这就会导致陷入局部最优解，直接影响算法性能。为了减小粒子陷进局部最优的概率，以便保持粒子的全局寻优能力，所以选择引入改进粒子群优化算法(Improved Particle Swarm Optimization，IPSO)，本文主要对学习因子c1、c2和惯性权重w进行改进。

2.2 PSO算法学习因子的改进

在粒子群优化算法中，c1和c2为加速系数，分别影响粒子的自我速度和其他粒子的影响所产生的速度。为了让群体能在全部的解空间中寻优，避免过早陷入局部最优，我们选择动态的调节加速度系数c1和c2的值，以达成随着迭代次数的增加，c1的值逐渐减小，c2的值逐渐增大，更方便全局寻优，提高算法收敛速度和精度。为此，取c1和c2分别如下：

(3)

c2=4-c1

(4)

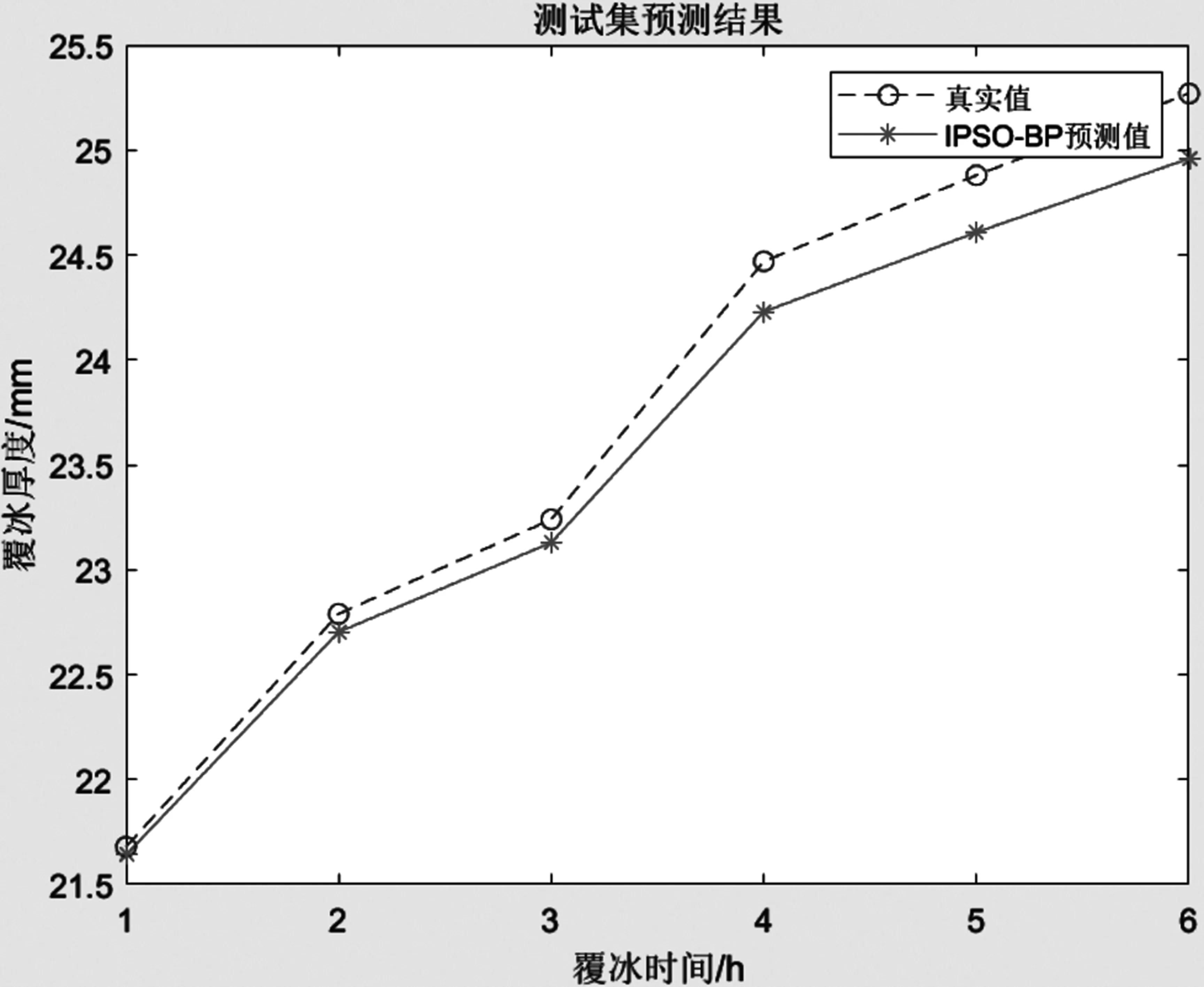
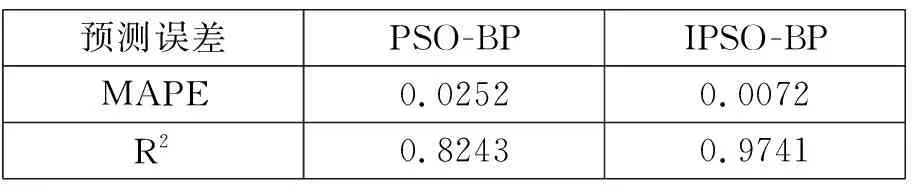
式(3)中Maxt和t分别为算法最大迭代次数和当前代数。cstart和cend为c1的初始值和最终值，0

2.3 PSO算法惯性权重非线性递减

在PSO算法中，惯性权重表示上一代粒子的速率对当前代粒子的速率的影响，惯性权重的大小影响着粒子全局寻优能力和局部寻优能力。因此选择引入权重控制因子，通过调节该控制因子的大小，进而来调整最大惯性权值在种群进化过程中所占的比例，这样能使得粒子在初期拥有较大的惯性权值进行全局搜索，在后期又能以较小的惯性权值进行局部寻优，其数学模型如式(5)所示：

(5)

式中wmax和wmin分别为惯性权重的最大值和最小值；t为当前代次数；Maxt为最大迭代次数。

2.4 IPSO优化BP神经网络

(6)

通过粒子在权值空间中不断搜索来使得输出层误差降到最低，粒子速度的变更也就更新了网络权值。

3 仿真分析

3.1 数据选取

为了测试该算法的效果，选用某输电线路36小时的连续覆冰过程数据，该组覆冰数据共36组，每组数据包括覆冰时长、温度、湿度、风速和覆冰厚度，一共180个数据，取温度、湿度、风速、覆冰厚度、覆冰时长作为输入特征矢量。选择前30组的数据用于训练，后6组数据用于测试。

3.2 参数设定

BP网络输入层节点数为5，隐含层节点数为5，输出层节点数为1；最大训练次数为100次；误差目标为0.0001；学习速率为0.1。

PSO参数设置为：惯性权重w=0.5；加速因子c1=2，c2=2。IPSO算法和PSO算法中最大进化迭代次数为100，种群规模N=20。IPSO中惯性权重最大值wmax=0.9，最小值wmin=0.1，加速因子cstart=4，cend=0.1。

3.3 实验结果

图1为BP模型和改进后的PSO优化BP模型的结果预测曲线图，从图1可以看出，BP模型在4小时节点出现了陷入局部最优，采用IPSO优化BP神经网络解决了局部最优问题，同时也拥有更高的精度。

图1 PSO-BP、IPSO-BP算法的误差预测

下表给出了PSO-BP、IPSO-BP的性能指标对比，MAPE为平均绝对值误差，该值越小表明模型预测效果越好，R2为决定系数该值越接近1表明模型拟合度越优。从下表可以看出改进后的IPSO-BP的预测误差明显小于改进前PSO-BP的预测误差，改进后预测曲线更贴近实际，拟合度更高。IPSO-BP的平均绝对百分比误差为0.0072，预测曲线无明显波动；决定系数R2为0.9741，接近1，与实际的拟合效果最优，说明改进后的IPSO-BP模型拥有更好的性能，预测精度更高。

各模型预测误差表

为了进一步验证改进后算法的有效性和收敛性，IPSO与PSO的适应度曲线如图2所示。

图2 PSO-BP与IPSO-BP的适应度曲线

从图2中可以看出，PSO在第17代左右陷入了局部最优，IPSO在第19代左右达到最优，IPSO曲线更接近于0，说明改进后的PSO避免了局部最优，在相同迭代次数下改进后的PSO算法拥有更快的响应速度以及更好的收敛性。

4 结论

为了提高覆冰预测的精度，本文提出一种基于IPSO优化BP神经网络的覆冰预测算法。针对覆冰厚度预测精度低的问题，基于BP神经网络，采用IPSO算法进行优化，避免人为选择BP模型参数带来的不利影响。针对 PSO易陷入局部最优问题，通过在PSO算法中加入学习因子和惯性权重的非线性变化，可以使改进后的算法拥有更强的全局寻优能力和收敛速度。通过选取数进行仿真，验证了改进后算法的优越性。