基于长短时记忆模型的信噪分离*

王先宇 张二华

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

语言是人类信息交流的主要途径，随着语音信号处理技术的不断发展，语音分离已经成为研究热点。在复杂的实际情况中，语音会受到各种干扰，给语音交流带来不利影响。例如：在日常对话中，过强的背景噪声可能会对语义的辨识及情感的判别带来困难；在封闭的机舱环境中，噪声会增加机组人员语音交流的难度；在人机交互中，噪声干扰会导致智能家居无法正常识别指令。采用信噪分离可有效提升语音识别的正确率，语音分离可作为其他语音处理技术的前端处理，为后续处理提供纯净、清晰的语音。

信噪分离是指从带有噪声的混合语音中提取目标说话人的语音信号。语音中包含的背景噪声会使混合语音变得模糊不清，而信噪分离能够削弱背景噪声并增强语音信号成分，有效提升信噪比和可懂度。相比由麦克风阵列采集的多通道语音，只由一个麦克风采集的单通道语音的分离难度更高，因为单通道混合语音中没有多通道语音中的空间信息，这增大了信噪分离的难度。

目前有多种信噪分离的方法。盲源分离是指从观测到的混合信号中分离出各原始信号分量，“盲”强调了两点：分离时各信号分量的相关信息，也无语音混合系数的相关信息。这种方法的局限在于，在低信噪比或阵发性噪声的条件下表现不佳。2006年以来，计算听觉场景分析（Computational Auditory Scene Analysis，CASA）日趋完善，能够较好地将分布于同一频带的多个声音信号进行分离［1］，但是计算听觉场景分析也存在局限，其分析所依赖的基音周期轨迹在低信噪比或阵发性噪声的条件下易受到干扰。

随着深度学习技术的发展，人们提出了更多基于深度学习的信噪分离算法，取得了较好的效果。冯利琪、江华等提出了一种深度神经网络与谱减法相结合的信噪分离算法［2］，能够显著提高分离语音的可懂度与信噪比，但分离结果与纯净语音信号相比仍存在差距。Jitong Chen、DeLiang Wang提出了一种以长短时记忆模型为基础的有监督信噪分离算法［3］，对于未知说话人或未知噪声的信噪分离都表现优异。Santiago Pascual、Antonio Bonafonte等提出了一种语音增强对抗神经网络算法［4］，使用对抗神经网络自动进行信噪分离，提供了信噪分离的新思路。Zhiheng Ouyang，Hongjiang Yu等提出了一种全卷积神经网络［5］，输入复数频谱进行信噪分离，这种方法不仅能进行振幅估计而且能进行相位估计，在节省内存空间的同时出色地完成信噪分离。

本文将理想浮值掩蔽作为训练目标，使用长短时记忆模型进行信噪分离，同时应用Griffin-Lim算法进行信号重构。本文还增加了消除窜音现象的步骤，能够减少分离语音中窜音的干扰。将本文算法与深度神经网络方法、卷积神经网络方法在多种噪声和信噪比条件下进行对比实验，评分结果表明本文的方法具有更好的信噪分离效果，可将STOI评分自卷积神经网络方法的0.41提升至0.62，将PESQ评分自卷积神经网络方法的1.08提升至1.53。

2 语音特征参数提取

2.1 梅尔频率倒谱系数

梅尔频率倒谱系数（Mel-Frequency Cepstral Coefficients，MFCC）是重要的语音特征。实验表明，人类的听觉感知并非呈线性关系，而是非线性关系。MFCC模拟了人类听觉感知的特点，为提取MFCC首先需要将频谱通过梅尔滤波器获得输出结果，再对输出结果求倒谱得到MFCC。梅尔滤波器体现了人耳听觉对于较高的频率成分具有较低的频率分辨力的客观规律。这些滤波器的带宽在低频区域较窄，在高频部分则较宽。滤波器的形态由许多等腰三角形组成，顶角处的权值为1，腰的起点处权值为0，该点也是上一个相邻滤波器的中心频率。图1为一个10阶的梅尔滤波器的示意图。

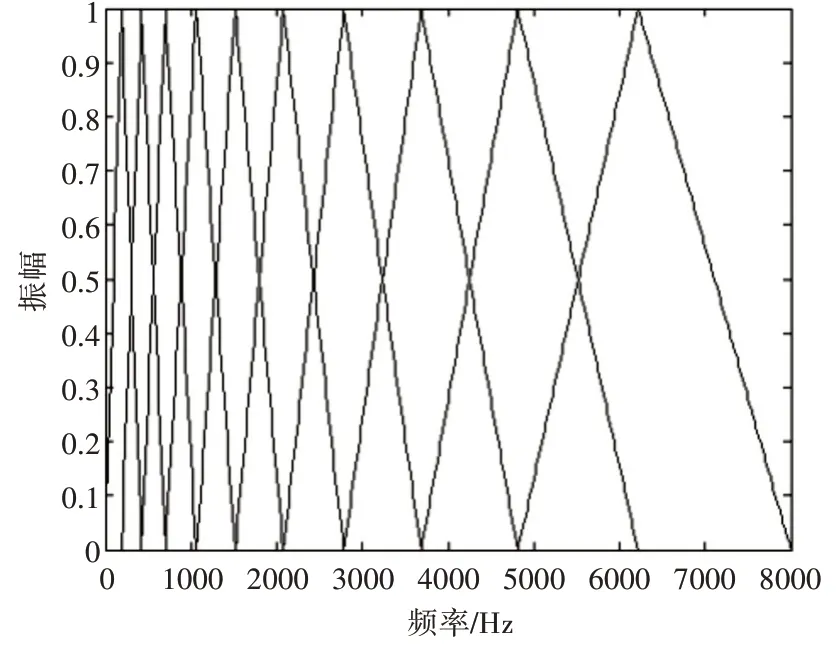
图1 一个10阶的梅尔滤波器示意图

当准周期脉冲激励进入声道时会引起共振特性，产生一组共振频率，称为共振峰频率或简称共振峰［8］。共振峰携带了可用于语音识别的信息，频谱的包络线能够反应共振峰的分布形态。而MFCC能够通过逆变换还原梅尔频谱的包络线。图2为某一帧语音前几维的MFCC重构梅尔频率包络线的效果，该语音采样率为16kHz，有效频率范围为0～8kHz，梅尔滤波器共48个，产生的MFCC共48维，其中前24维MFCC在大致还原梅尔频率包络线的同时有较少的细节丢失，因此取前24维作为MFCC参数的维数是适合的。

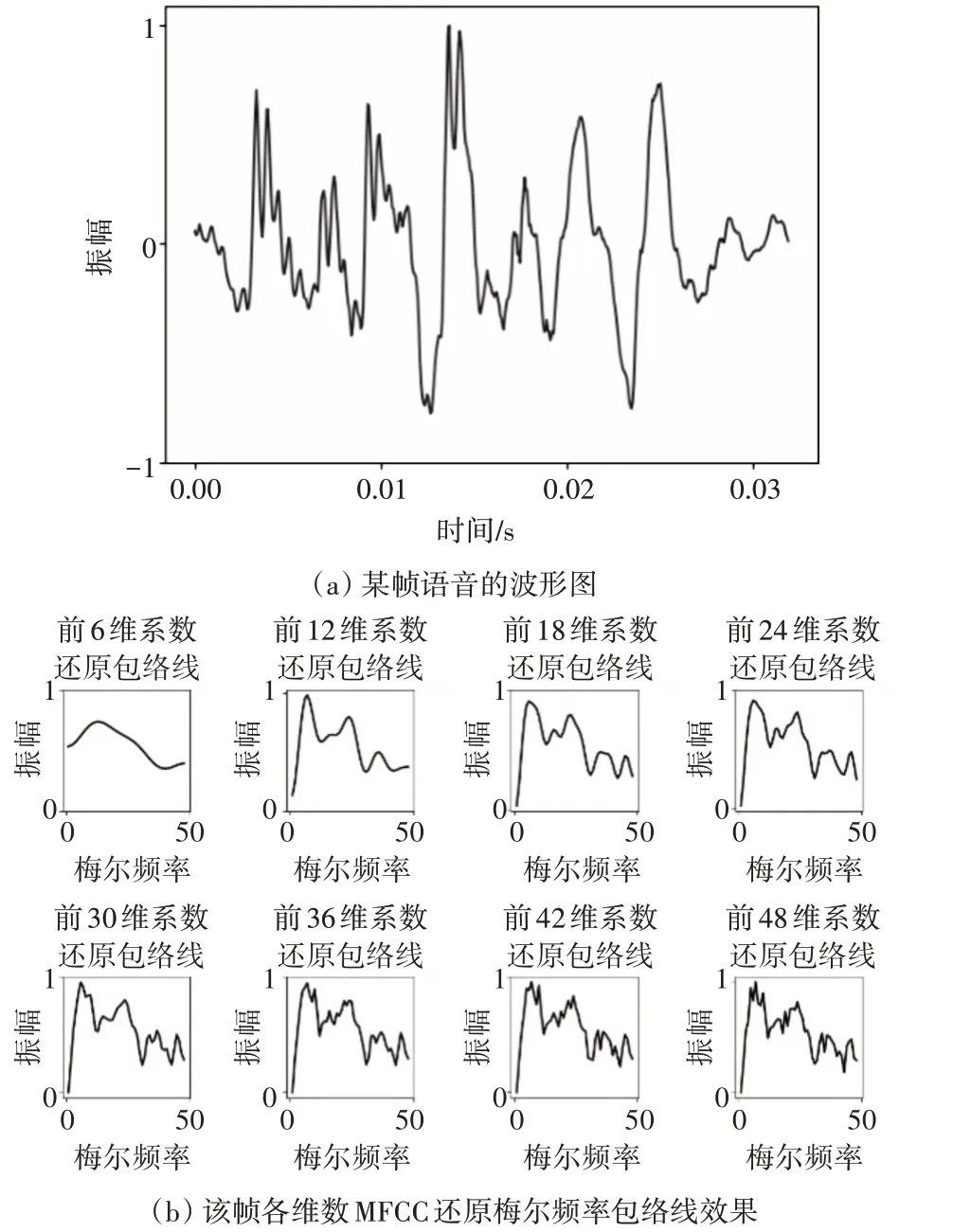
图2 各维数MFCC还原梅尔频谱包络线的效果对比

2.2 理想浮值掩蔽

使用时频掩蔽进行有监督语音分离时，分离语音的频谱为时频掩蔽与混合信号频谱的哈达玛积（Hadamard product），如式（1）所示：

其中，为混合语音振幅谱，为模型输出的时频掩蔽估计值，为分离语音的振幅估计，*为矩阵的哈达玛积运算。

理想浮值掩蔽是理想二值掩蔽的改进。理想浮值掩蔽表示在混合语音某时频单元中，目标语音成分相对于混合语音的占比，其定义为

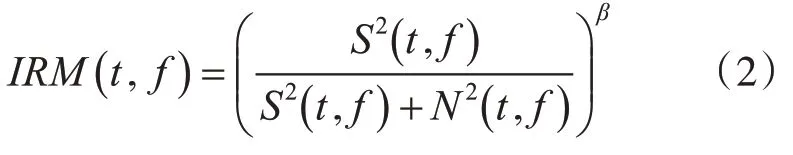
其中，t、f分别表示该时频单元所在的时间帧序号和频率点序号。S(t，f)和N(t，f)分别代表语音和噪声在该时频单元中的傅立叶变换系数［6］，其平方为能量，β是可调节因子，一般设为0.5。IRM假定纯净语音与噪声相互独立，其取值为［0，1］上的实数。

3 叠接相加法的缺陷与改进方法

窜音现象是指在分离语音中仍然能够听见噪声。窜音现象是由频率掩蔽效应产生的。本文分离语音信号重构中还使用了一种振幅平滑的方法，在振幅估计中能够观察到振幅较大的时频单元组成的类似谐波结构，根据相同频率前后帧的时频单元的振幅，对不在类似谐波结构中的时频单元的振幅进行平滑，这一步骤能够略微缓解窜音现象。

以时频掩蔽作为训练目标的深度模型方法都需要进行分离语音信号波形重构，因为模型估计得到的时频掩蔽不是真正的波形信号，需要经过掩蔽还原得到频谱，再经过波形重构才能获得完整连贯的分离语音。分离语音信号重构采用叠接相加法与Griffin-Lim算法。

3.1 叠接相加法及其缺陷

叠接相加法需要将频谱振幅与相位谱还原为复数谱。对复数频谱进行傅立叶逆变换，得到分离语音的波形信号。最后将各帧按原本分帧的位置对齐后对应相加，多次重叠部分取均值，最终得到了完整的分离语音。

传统的叠接相加法中使用的相位为混合语音的相位，这意味着，有一部分噪声的相位进入了分离语音。虽然人耳对初始相位不敏感，但是对于相位的连续性很敏感。近年来越来越多的学者认为，相位在信噪分离中也有重要的作用［5，19］。由于混合语音的频谱是纯净语音频谱与噪声频谱的矢量和，混合语音的相位可能与纯净语音的相位相差较大。即噪声相位的介入会导致分离语音受到干扰。因此，使用混合语音的相位进行信号还原存在一定的缺陷。

3.2 Griffin-Lim算法

Griffin-Lim（G-L算法）由Daniel W.Griffin和Jae S.Lim于1984年提出，是一种只利用振幅谱重构语音波形的方法，而无需借助相位。G-L算法的过程是：

1）使用随机的相位谱与现有的振幅谱通过傅立叶逆变换得到时域信号，并将各帧叠接相加得到完整的语音波形。

2）对得到的语音信号分帧、加窗并进行傅立叶变换，得到新的相位谱与振幅谱。

3）舍弃2）中的振幅谱，只利用2）中的相位谱与初始的振幅谱进行傅立叶逆变换得到时域信号并将各帧叠接相加得到完整的语音波形，再回到步骤2），或达到最大迭代次数。

在G-L算法的迭代过程中，振幅谱保持不变，相位谱不断收敛最终获得连续、渐变的重构语音相位。

G-L算法在重构波形时无需借助混合语音的相位，这有效地避免了混合语音和噪声对于分离语音相位的破坏。利用G-L算法进行分离语音的波形重构，能有效解决信噪分离时无法进行相位分离的问题，使分离语音不仅振幅接近纯净语音并且相位保持连续渐变，能够全面提升分离语音质量。

4 实验设置

本文实验使用的语音库为南京理工大学NJUST603语音库，包含男、女生各200余人朗读文章。其中T4语音库的语料为作家刘绍棠所著《师恩难忘》的朗读，包含593个汉字。本次实验的训练集中男女声各17段共34段纯净语音片段，每段语音长约1s，采样率为16kHz。生成混合语音时使用的噪声包含白噪声、狗叫噪声、冲激噪声、战斗机噪声、水流噪声五种，其中狗叫噪声和冲激噪声为阵发性噪声，白噪声、战斗机噪声和水流噪声为平稳噪声，信噪比分别为-3dB、0dB、3dB、6dB、9dB、12dB、15dB、18dB，生成的训练语音集共有1360段混合语音。

本文的算法使用长短时记忆模型进行分离。算法首先提取10帧的MFCC作为输入特征，维度为240维，经过线性变换输入隐含层。长短时记忆模型中共有三层隐含层，每层共有512个节点，随机遗忘因子设置为0.5，最后一层隐含层后接一层257个节点的输出层，对应IRM的0-256样点（0～8000Hz低频部分），该输出是10帧窗口中最后一帧所对应的IRM估计。隐含层中的随机遗忘因子设置为0.5。网络采用Adam优化器以10-5的学习率进行网络优化，在随机初始化后根据后向传播调整网络参数。

实验的测试集使用训练集之外的男女生各3个说话人共6段语音，生成混合语音时使用的噪声与训练集相同，信噪比分别为-3dB、0dB、3dB、5dB、10dB、20dB，生成的测试语音集共有180段混合语音。

本文算法的分离结果与DNN方法以及CNN方法的分离结果进行了对比，其中DNN的网络结构为3层全连接层，每层各1024个节点，输出层有257个节点。CNN中有两层卷积层与两层池化层以及3层全连接层，卷积核大小为3*3，池化窗口分别为3*3和2*1，全连接层中各1024个节点，输出层有257个节点。

本文采用的分离语音评价指标为短时客观可懂性STOI（Short-Time Objective Intelligibility）与客观语音质量评估PESQ（Perceptual Evaluation of Speech Quality）［9］。STOI基于语音的离散傅立叶变换结果在短时的时频区域内计算可懂度指标［9］，其评分取值范围为（0，1），数值越高则表明分离效果越好。PESQ是ITU-T P.862建议书中的客观指标，是客观上MOS值（Mean Opinion Score）的近似值。PESQ的取值范围为（-0.5，4.5），数值越高则表明分离质量越好。

5 结果分析

评分结果按照噪声类别与信噪比进行分组，每一组中的STOI评分与PESQ评分取均值，分离结果的评分如表1和表2所示。由于结果相似，此处省略了10dB与20dB信噪比的分离结果评分。分析以冲激噪声、水流噪声和战斗机噪声为例。

在分离带有冲激噪声的混合语音时，噪声较强的时频单元中局部信噪比较低，宏观结果就是分离语音中有明显的窜音现象。如果采用CNN方法，例如在冲激噪声-3dB信噪比的情况下分离语音的STOI评分只有0.41，PESQ评分只有1.12，分离效果较差。在相同噪声条件下，本文方法的分离结果明显优于CNN方法的分离结果，窜音现象明显减少，目标语音成分更加清晰。在表1中，采用本文的方法，在冲激噪声-3dB信噪比的情况下，分离语音的STOI评分由CNN方法的0.41提升至0.62，PESQ评分由1.12提升至1.53。其中G-L算法进行相位分离，发挥了重要作用。

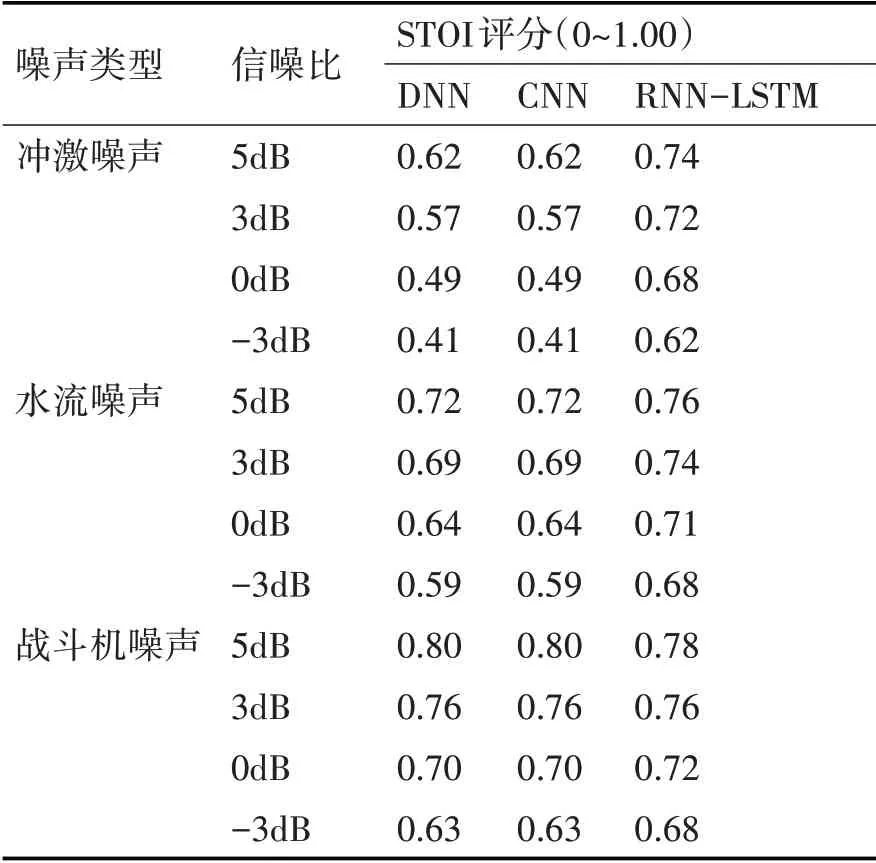
表1 不同方法信噪分离结果的STOI评分

在平稳噪声的情况下，本文方法的分离结果评分比CNN方法和DNN方法略高。在表2中，采用本文的方法，在平稳噪声战斗机噪声-3dB信噪比的情况下，本文提方法同样相对于DNN与CNN方法略有提升，STOI评分略高0.05，PESQ评分可提升0.19。在水流噪声各信噪比的情况下，本文方法的分离结果评分都比CNN、DNN的方法略高。虽然本文的方法的分离指标评分与CNN和DNN方法提升较少，但在实际听感上则清晰很多，窜音现象明显减弱，这是客观评价指标难以度量的。

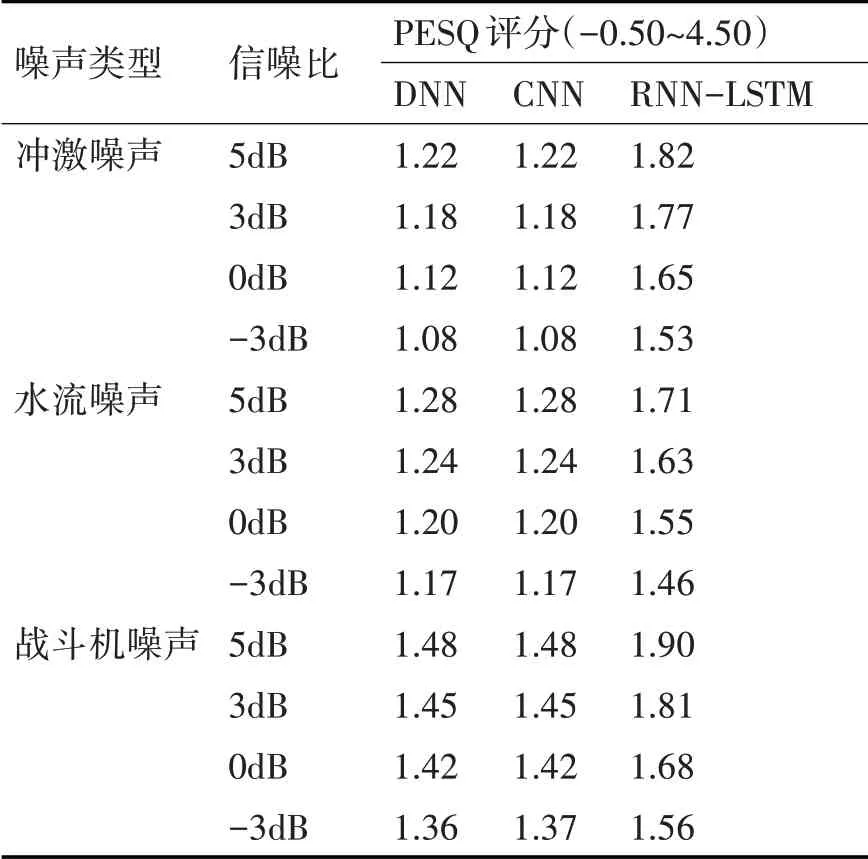
表2 不同方法信噪分离结果的PESQ评分

6 结语

从本文的实验结果看出，使用长短时记忆模型进行掩蔽估计、使用G-L算法进行波形重构的信噪分离方法，分离效果相较于DNN与CNN方法有明显的提升。应用G-L算法进行语音重构，较好地解决了信噪分离无法进行相位分离的问题。同时可以看出，本文研究的算法对于阵发性噪声混合语音也能正常分离，但在低信噪比情况下的表现仍然有待提升。由此可以看出对于低信噪比的情况，信噪分离任务依很艰巨，随着更多深层网络结构的提出，信噪分离效果一定能够得到更大的提升。