由一道调研试题引发的深度探究

江苏省太湖高级中学 翟洪亮（邮编：214125）

当今世界进入大数据时代，为了适应科学技术发展，“概率与统计”已成为大学数学教育的基础课程之一，地位在逐渐上升. 为了加强中学数学教育与大学数学教育的衔接，《普通高中数学课程标准（2017 年版）》也将“概率与统计”作为高中数学课程的四条内容主线之一，贯穿整个高中数学课程.“概率与统计”内容成为高考的必考知识点，常以解答题形式出现，由于2019 年高考数学全国卷Ⅰ理科21 题与数列知识进行综合考查，颠覆了人们对概率与统计试题不能作为压轴题的认识，影响各地调研命题方向，如2021 年江苏省南通市如皋调研试卷20 题.

1 试题

为进一步加强未成年人心理健康教育，如皋市教育局决定在全市深入开展“东皋大讲堂”进校园心理健康教育活动. 为了缓解高三学生压力，高三年级某班级学生在开展“东皋大讲堂”过程中，同座两个学生之间进行了一个游戏，甲盒子中装有2 个黑球和1 个白球，乙盒子中装有3 个白球.现同座的两个学生互相配合，从甲、乙两个盒子中各取一个球，交换放入另一个盒子中，重复n次这样的操作.记甲盒子中黑球个数为Xn，恰好有2 个黑球的概率为an，恰有1 个黑球的概率为bn.

（1）求第二次操作后，甲盒子中没有黑球的概率；

（2）求X3的概率分布和数学期望E(X3).

解（1）设“第二次操作后，甲盒子中没有黑球”为事件A，

（2）设重复n次这样的操作后，甲盒子中有0个黑球的概率为cn，

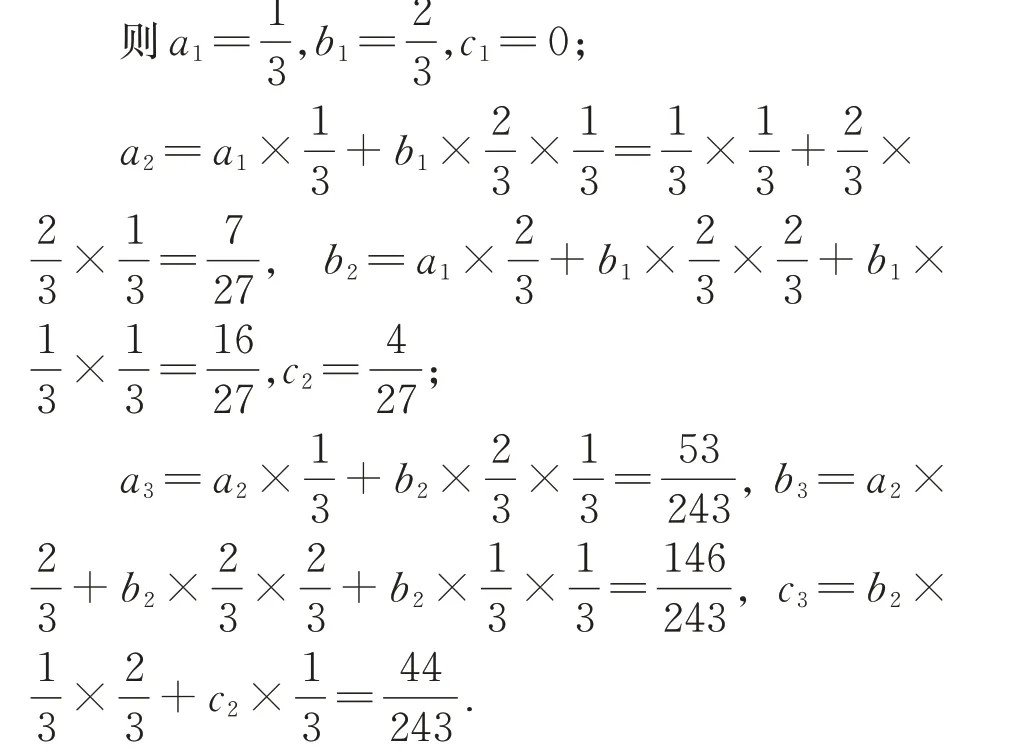
故X3的概率分布为：

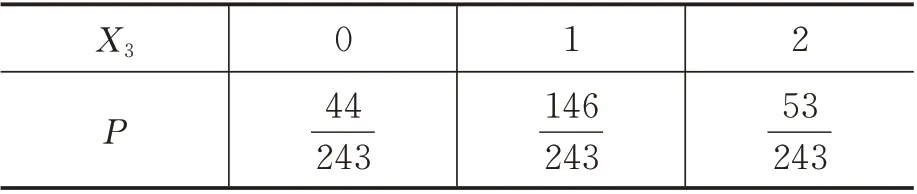
X3 P 0 1 2 53 243 44 243 146 243

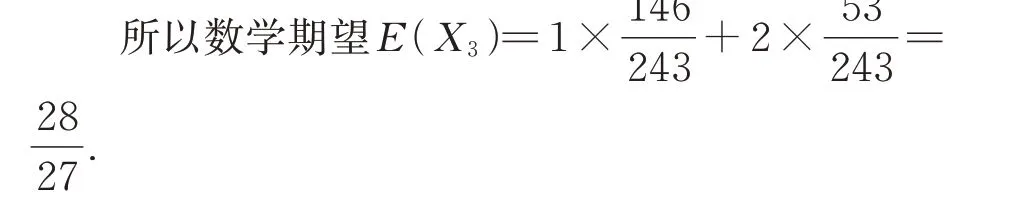
2 联想

由此联想到2020 年江苏高考数学理科卷的23 题：

甲口袋中装有2 个黑球和1 个白球，乙口袋中装有3 个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n次这样的操作，记甲口袋中黑球个数为Xn，恰有2 个黑球的概率为pn，恰有1 个黑球的概率为qn.

（1）求p1，q1和p2，q2；

（2）求2pn+qn与2pn-1+qn-1的递推关系式和Xn的数学期望E(Xn)(用n表示) .

所以Xn的分布列为：

Xn P 0 1 2 1-pn-qn qn pn

故Xn的分布列为：

Xn P 0 rn 1 2 qn pn

3 探究

探究1 当黑球数量大于2 时，利用矩阵不便逐一求出随机变量对应的概率，是否可以通过整体构造等比数列求解？

甲口袋中装有3 个黑球和1 个白球，乙口袋中装有3 个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n次这样的操作，记甲口袋中黑球个数为Xn，恰有3 个黑球的概率为pn,3，恰有2 个黑球的概率为pn,2，恰有1 个黑球的概率为pn,1.

故Xn的分布列为：

Xn P 0 1 2 3 1-pn,1-pn,2-pn,3 pn,1 pn,2 pn,3

这说明，当黑球数量大于2 时，仍可通过整体构造等比数列求解. 从甲、乙两口袋中各任取一·个·球交换放入另一口袋，在求第n次操作后甲口袋中有k个黑球的概率时，关键是要分清两类情况：一是当k不取最大时，需要考虑第n-1 次操作中三种情况下的概率：当甲口袋黑球个数为k+1 时，是从甲口袋中取一个黑球换回乙口袋中一个白球；当甲口袋黑球个数为k时，可以从甲口袋中取一个黑球换回乙口袋中一个黑球，也可以从甲口袋中取一个白球换回乙口袋中一个白球；当甲口袋黑球个数为k-1 时，是从甲口袋中取一个白球换回乙口袋中一个黑球.二是当k取最大时，需要考虑第n-1 次操作中两种情况下的概率：当甲口袋黑球个数为k时，是从甲口袋中取一个白球换回乙口袋中一个白球；当甲口袋黑球个数为k-1 时，从甲口袋中取一个白球换回乙口袋中一个黑球.

探究2 若把试题推广到一般形式，是否可以通过整体构造等比数列求解？

甲口袋中装有a个黑球和b个白球，乙口袋中装有c(c≥a)个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n次这样的操作，记甲口袋中黑球个数为Xn，恰有a个黑球的概率为pn,a，恰有a-1 个黑球的概率为pn,a-1，...，恰有2 个黑球的概率为pn,2恰有1 个黑球的概率为pn,1.

（1）求p1,a，p1,a-1，p1,a-2，...，p1,1，p1,0；

（2）求Xn的数学期望E(Xn)(用n表示) .

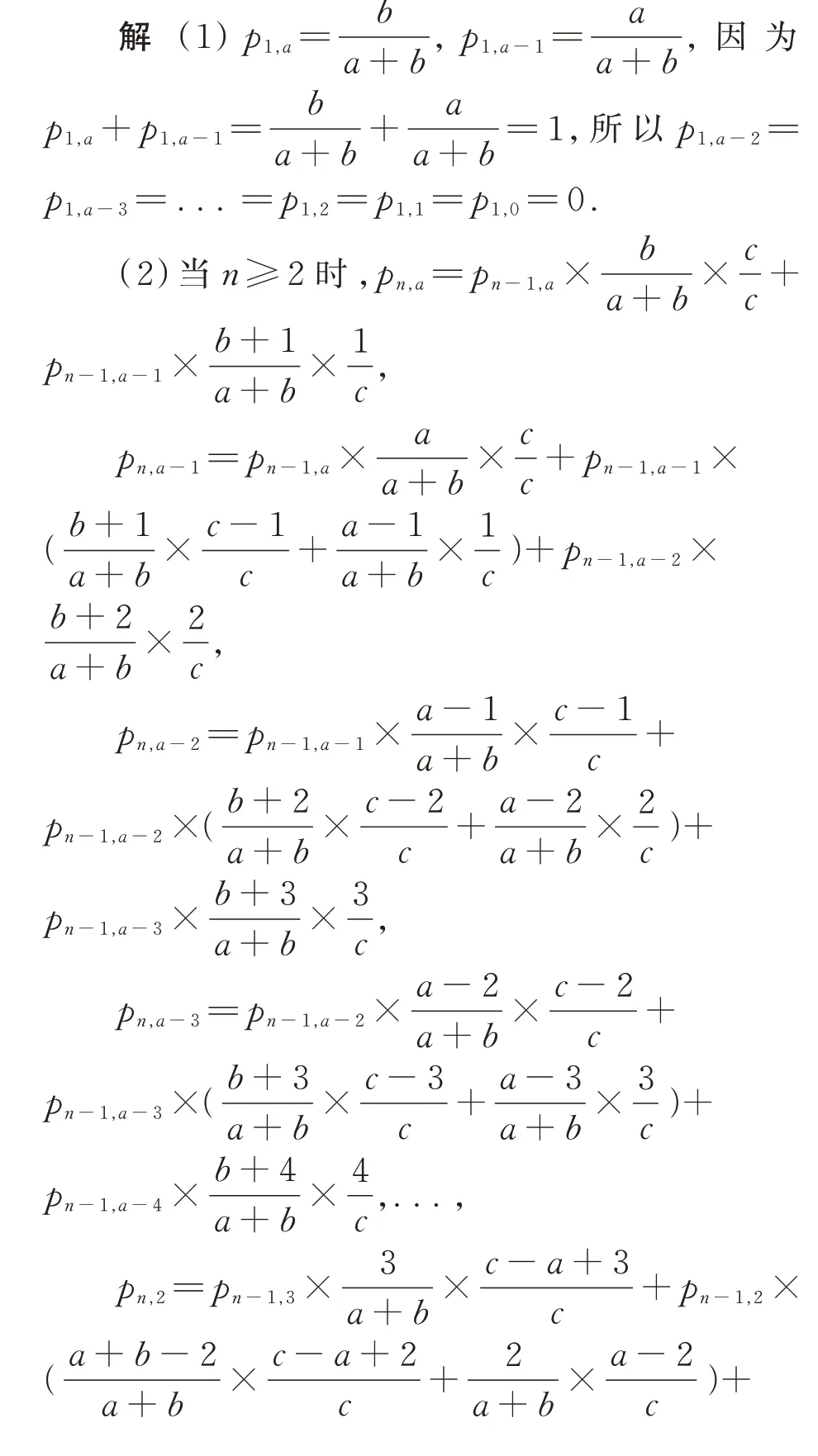
故Xn的分布列为：

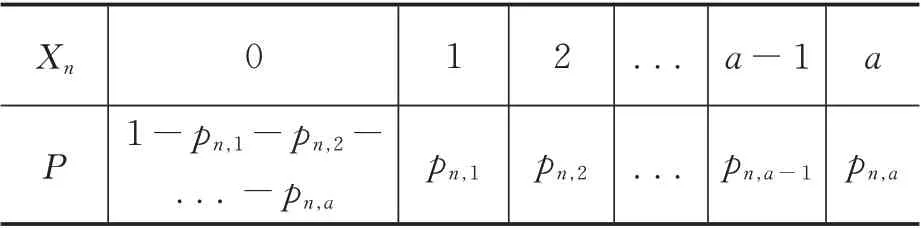
Xn P 0 1 2...a-1 a 1-pn,1-pn,2-... -pn,a pn,1 pn,2...pn,a-1 pn,a

从而可得重复n次操作后甲口袋中黑球个数为Xn的数学期望与两个口袋中黑白小球数量之间的内在规律.