基于双层模型的票价信息智能优化算法仿真

唐艺凡， 冯娜， 庞婷婷

(西安交通工程学院， 交通运输学院， 陕西， 西安 710000)

0 引言

近年，随着我国高速铁路规模的扩大和网络信息技术的发展，高速铁路的控制和管理向着智能化和信息化的方向发展。其中，对于铁路车票的定价问题，若仅采用单一的定价方案，会使得高峰时间段的车次售票达到饱和，空闲段的车票售出率偏低，一方面造成客流集中，不利于客流的分流和疏导，增大铁路运输压力，另一方面未能实现铁路运营效益的最大化，造成公共资源浪费[1-2]。研究如何通过优化票价实现铁路资源的充分利用和效益提升具有重要研究意义。本文从铁路部门和乘客两个层面进行分析，构建出行成本函数，提出多种票价调整策略，对票价调整问题建立双层模型，上层模型为售票效益函数，下层模型为出行路径选择函数，建立上下层之间的关联函数关系，通过数学优化方法，实现售票效益的提升和车票售出率的均衡。

1 双层优化模型建模

在铁路票价制定过程中，铁路管理部门通过调整票价，在一定程度上影响乘客的出行规划，以优化广大乘客的出行费用。乘客具有自主选择能力，根据自身对经济性、快速性、便捷性、舒适性等因素的考虑，对比现有的多种出行方案，选择认为最为合适的出行方式。铁路车票的定价需要兼顾铁路运营部门和乘客两方面的因素，二者的关系与Leader-Follower关系相一致，即铁路运营部门担当决策者(Leader)角色，乘客则充当跟随者(Follower)的角色，可利用双层模型对车票定价机制进行建模，通过模型参数调整实现对票价的优化调整。双层模型主要包括上层规划模型和下层规划模型2个主要部分，两层模型分别建立各自独立的目标函数，两层模型之间存在着关联变量，双层模型优化算法的目标是同时满足双层模型的目标函数最优化，解算出最优解。双层模型中，上层模型为铁路管理部门的收入函数，其目标是为了实现获益最大化，下层模型为乘客选择函数，其目标是实现乘客出行选择最优化，通过双层模型的关联，使得铁路部门收益和乘客出行选择均实现最优。

1.1 上层模型函数

上层模型主要是指铁路运营部门的售票收入，可将售票总收入设定为FS，其值为不同票价和客流乘积的总和，公式表示为

FS=qn(Pn)Pn

(1)

式中，n表示行程的总类别，qn表示客流量，Pn表示票价。

铁路运行过程存在成本消耗，可将运营成本主要划分为列车运行费用、设备损耗费用、水电费用、管理费用等4大类，公式可表示为

C=C1+C2+C3+C4

(2)

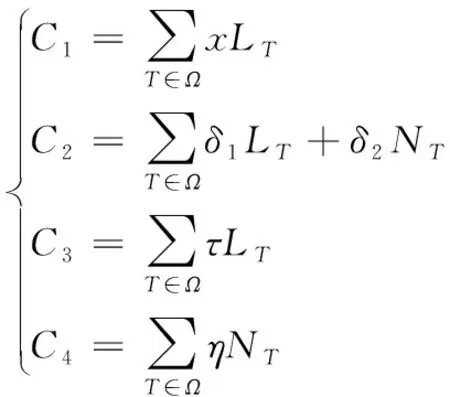
(3)

式中，C表示运营的总成本，C1表示列车运行费用，C2表示设备损耗费用，C3表示用电费用，C4表示管理费用，LT表示线路的长度，NT表示行程经过的车站数量，x表示列车每运动一公里所需的费用，δ1表示列车一公里所耗电费，δ2表示列车在车站停留所耗电方，τ表示单公里车辆实用费，η表示车站服务成本。

铁路部门属于盈利单位，售票总收入整体上要超出铁路运营的总成本，约束条件1可表示为

qn(Pn)Pn≥C

(4)

另外，由于铁路服务属于公共事业，需要保障社会公共服务和运营稳定性，一般国家会对票价设定上限，约束条件2可表示为

Pn≤Pn，max

(5)

车票定价最优化模型可表示为

maxFS=qn(Pn)Pnst:Fs≥CPn≤Pn，max

(6)

1.2 下层模型函数

下层模型主要描述乘客的行程选择，乘客的出行选择受票价、时间、快速性、舒适性等属性因素影响[3]，采用指数函数描述下层模型，选取出行方式的属性作为函数的变量，下层模型的描述函数可表示为

Fx=μ(qn)ϖ-αtn-βpn+γcn

(7)

式中，w表示待确定的参数，t表示列车运行的时长，p表示车票价格，c表示其他综合因素综合(一般取值范围为0.15～0.25)，α表示受到时间因素的影响系数，β表示受到票价因素的影响系数，γ表示受到综合因素的影响系数，影响系数β会随票价的变动而发送变化。

乘客在选择出行计划时，会在一定程度上受到票价的影响，一般情况下票价越高的出行方式对乘客的吸引力越低，反之，票价降低则会吸引更多的客流量。但从整体市场规律角度上看，客流总流量基本在一个稳定的水平，在总客流量稳定的情况下，票价和客流量的关系[4-5]可表示为

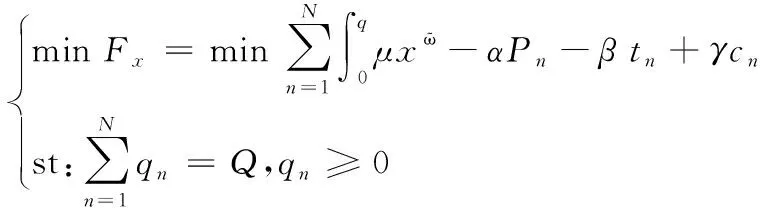
(8)

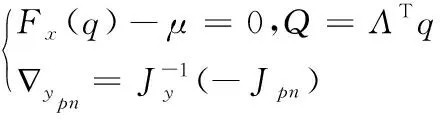
(9)

Jocobi矩阵运算可以获得n种客流量与票价间的偏导数(∂qn/∂pn)，其偏导数反应出乘客需求量，利用泰勒展开式，下层模型的函数可表示为

(10)

2 算法软件设计

在票价的调整过程中，其算法的设计主要包括票价调整策略和双层模型求解2个部分。首先给出票价的具体调整策略，然后按照不同的调整策略对双层模型进行求解，输出票价的最优解。

2.1 票价调整策略

票价调整是指在允许的票价范围内，依据车票售出率对不同区段的车次进行分类，通过调整票价将车票的售出率保持高于60%，同时低于100%[7]。在售票率区间(60%，100%)中，挑选出2个调整点，分别为75%和85%。当车票的售出率低于75%时将票价向下调整，当车票的售出率高出85%时将票价向上调整，以实现乘客引导和分流，控制区段客流量，使得列车车票售出率尽量保持在(60%，90%)区间中。不同的票价调整先后顺序和调整幅度对客流的均衡 控制和售票收益具有不同的影响，这里给出3种票价调整策略[6-7]，如表1所示。

表1 票价调整策略

2.2 双层模型求解

双层模型的求解问题具有非凸特性，是模型求解的难点所在，解决问题的关键在于求出上层模型和下层模型之间的关联函数，即描述客流和票价之间的影响关系[8-10]。本文设计的求解流程：首先对下层模型进行求解，输出当前票价情况下的客流量，然后将得到的客流量代入上层模型，对上层模型求解输出售票收益和售票率，依据售票情况和票价调整策略对票价进行更新；然后将更新后的票价数据重新代入下层模型进行求解，依次循环迭代直到售票收益达到极大值，则算法迭代完成。模型求解流程如图1所示。

图1 模型求解流程

3 仿真分析

以某固定行程区间内的所有高铁车次信息为研究对象，每个车次可承载乘客数量均设定为600，为了简化计算量，仅对二等座票价进行分析。按照铁路的相关规定，列车的售票率与该区间段内分配的车票数目相关，这里假定每个车次的车票售出率均为70%，按照票价浮动范围要求，该区间段的票价调整范围为470～580元。利用MATLAB软件对模型进行迭代求解，迭代步数设定为1 000，按照上文表中的3种票价调整策略分别进行迭代调整，在3种不同票价调整策略下售票总收益结果如图2所示。

图2 售票收益仿真结果

由售票收益迭代结果可以看出，与为调整前的票价收益相比，通过策略二和策略三调整后收益均得到提升，实现了提升售票收益的目的。策略二对售票收益提升的幅度更高，且其需要进行的迭代次数更少。策略一进行调整后，其售票收益值与调整前相比更低。通过该方法可筛选出收益最高的调整策略，从而实现对票价调整策略的对比和验证。文中研究对象行程区间内的初始实际收益为175万元，策略二迭代优化后的最大收益为194万元，提升了10.8%。

票价调整前后列车的车票售出率如图3所示。由图中曲线可知，通过票价调整，3种调整策略对客流分配均具有均衡作用，使得该区间段内的各车次座位售出率均处于允许范围内，平滑了极值点，避免出现个别车次过分拥挤，而其他车次过分空闲，从而实现客流吞吐量的均衡。3种方案对客流的调整效果基本接近，使得售出率极高点平均下降了10%左右，售票率极低点平均提升了7%左右。其中，策略二的售出率变化更为平稳，车次售出率分布更为均衡，在车票售出率调整方面更具一定的优势，综合对比策略二在票价调整效果上具有更突出的效果。未进行优化调整的实际运行情况中，第4～7车次的平均售票率达到98%，客流达到拥堵状态，通过策略二优化调整后，该高峰段的平均售票率下降至86%，下降了12.2%，有效缓解了出行高峰期的拥堵情况。

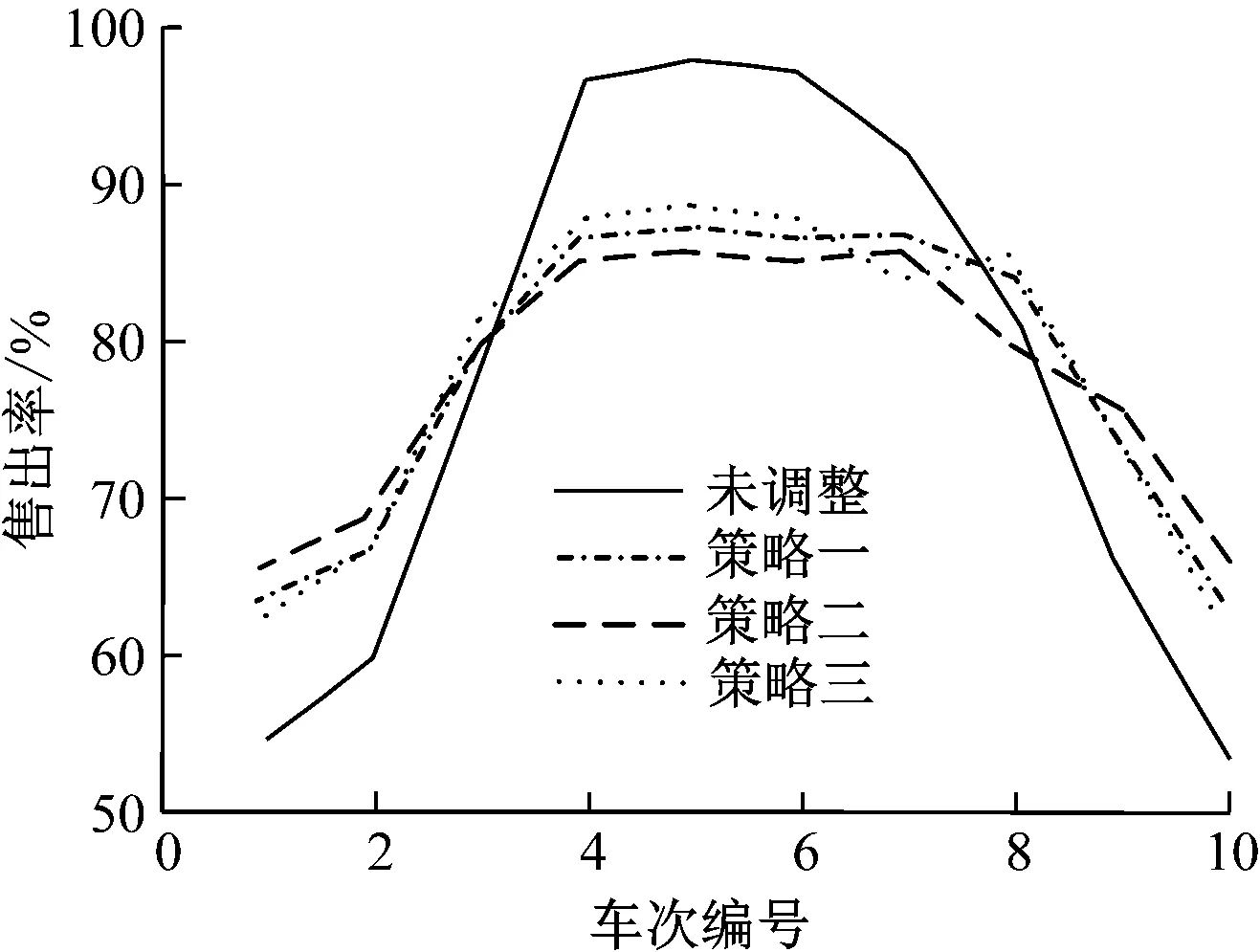
图3 车票售出率仿真结果

4 总结

本文研究了铁路票价调整问题，分析票价调整对铁路运营收益和客流分配的影响，利用双层模型对票价调整进行建模，并设计了模型迭代与求解过程，给出了3种票价调整策略，将3种调整策略代入模型进行仿真，仿真结果验证了算法的有效性。实际的票价调整策略具有多样性，不同的调整顺序和幅度组合可构成不同的调整策略，而不同策略对客流分配、售票收益及乘客出行选择的影响可进行更为深入的研究。影响票价的因素包括政策、经济建设、乘客需求、市场竞争等多种因素，目前研究方向可概括为单一票价、多级票价、动态票价等3个主要方向，采用的方法策略具有多样性，包括为非线性整数规划模型、多级票价体系策略、运量与运价模型、依据市场变化调整定价策略等等，有待进行更进一步的研究。