基于灰色关联分析的大学生就业质量评价研究

陈倩

(商洛学院,电子信息与电气工程学院， 陕西，商洛 726000)

0 引言

当代社会发展的重要问题之一就是就业，促进就业是实现全社会人民生活稳定的关键之一，就业质量的优劣直接反映国民经济发展趋势与国家社会稳定情况。高校大学生是社会储备人力资源，也是国家未来发展的储备力量，因此研究高校大学生就业质量问题显得尤为重要[1]。目前已有研究中，评价大学生就业质量的相关研究受到诸多社会及经济因素的影响，导致评价体系不够科学、客观、完整和全面，存在诸多干扰因素。大学生就业质量评价的结果直接影响高校的办学水平，只有做到科学、系统、客观的就业质量评价才能有助于高校、社会、毕业生的长久发展。随着我国教育水平的提高，大学生就业质量优劣已经是衡量高校办学水平的重要指标，经数据分析得到的指标关联度并且通过计算得到权重，综合评价系数分析大学生就业质量，以此为参照，督促高校做出改革，提升教学质量。

针对大学生就业质量评价，有学者提出基于个体问卷数据的大学生就业质量分析，使用问卷调查法分析并测算大学生就业质量，主要目的在于数据统计分析，缺乏科学性；还有学者提出基于组合群验模型的大学生就业竞争力评价方法，该方法使用数学模型评价大学生就业质量，具有一定的参考性，但是过程过于复杂。

灰色关联分析是一种十分活跃的灰色系统理论之一，基本理论是几何形状判断不同序列之间联系紧密与否依据序列曲线。关联度就是度量2个系统间因素随着对象和时间变化的关联性大小，假如2个因素存在一致的变化趋势，说明具有较高的同步变化程度，也可以说二者具有较高的关联程度；如果2个因素的变化趋势不一致，则说明关联度较低[2]。由此可以证明灰色关联分析法是依据因素发展趋势相异程度以及发展趋势来判定的，主要用于衡量因素之间的关联程度。灰色关联分析具有较高可靠性，构建灰色关联分析模型计算各指标关联度情况，计算过程中把样本数据作为模型，因此实际计算时所需样本数量较少，不需要使用典型的数据分布方法，实际计算结果和定性分析结果具有高度一致性。定量分析系统发展态势以理论数学为基础，确定数个比较数列和参考数列2个关联系数的关联度。灰色关联度分析能够量化比较分析系统态势，实质上就是对参数数列与比较数列的曲线几何形状接近度进行比较，灰色关联度分析的实质就是评价对象的优劣次序，以此获得最终的评价结果。本文将灰度关联分析方法作为基础，综合评价大学生就业质量，为高校未来教学发展提供了目标方向。

1 大学生就业质量评价

1.1 指标体系构建

大量分析相关文献，统计大学生就业质量评价研究状况，结合专家法[3]确定大学生毕业质量评价指标体系，结果见图1。

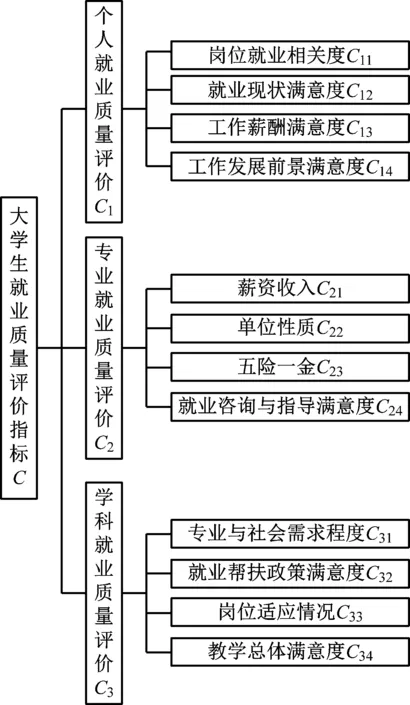
图1 评价指标体系

在图1中，C为目标层，第二级为方案层，第三层为准则层。综合参考文献和高校就业指导中心专家、教师的相关指导意见分析考评后，根据指标选取要求的宏观性、通用性、简易性、可比性[4]筛选出具有代表性的12个就业质量评价指标，主要从个人、专业和学科3个方面开展就业质量评价，具有较强的客观性。

1.2 基于灰色关联分析的学生就业质量评价方法

在构建了大学生就业质量评价指标体系后，运用灰色关联分析模型求解每个就业质量评价指标与就业质量的关联度。构建数据矩阵，并采用均值化方法对各数据进行无量纲化处理，构建各指标数据的灰色关联矩阵，并计算关联度，据此确定各指标的权重，将各评价指标分值与权重相乘，并对乘积结果加和，得到就业质量评价结果。

1.2.1 构建数据矩阵

假设分别存在m个评价对象和n个评价指标，可使用Ui表示大学生就业质量综合评价指标集，其中i=1,2,…,n。

使用式(1)表示数据矩阵：

(1)

1.2.2 无量纲化处理

各个指标的数量级和计量单位均存在差异，各指标之间缺乏综合性，所以无法开展综合性分析，为解决这种问题，必须使用数学化标准方法处理这种差异，本文开展无量纲化处理时使用均值化方法[5]。

均值法是各个变量的变量值与变量相除，获得变量的平均值，这种方法不但能够将数量级和无量纲造成的影响消除，同时还能保留每个变量取值差异程度信息，去除综合指数受到差异程度较大的变量[6]，进而减少了对差异较大的变量的处理步骤，缩短了数据的处理时间，提高就业质量评价数据的处理效率。使用无量纲化的均值化方法处理各个指标量：

(2)

(3)

1.2.3 构建灰色关联矩阵

确定无量纲化处理后的数据矩阵：

(4)

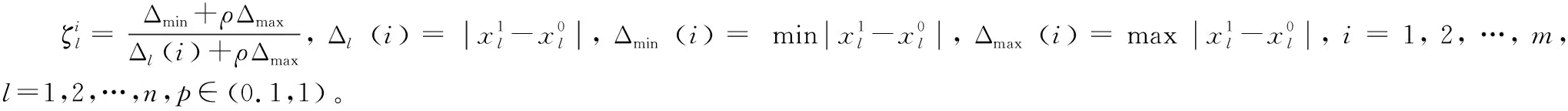
1.2.4 计算关联度

通过式(4)计算关联度：

(5)

其中，γi代表第i个指标和评价综合指数之间的关联度。根据式(5)和灰色关联矩阵，经MATLAB环境编写指标关联度计算程序，获得各个指标关联度大小[8]。

1.2.5 指标集权重确定

灰色关联分析仅能分析指标关联度，为使评价结果更加具有准确性和科学性，使用基于改进层次分析法计算权重，实行综合评估大学生就业质量评估。

在评估过程中，权重占据重要作用，常见的层次分析法所使用的方法为9标度法建立指标判断矩阵，但是在实际应用过程中考虑到众多指标都存在满意度评价，而且满意度界定存在严重干扰影响分辨判定，导致权重主观具有较强的随意性，造成评价可靠性和客观性都受到影响[9]，所以使用最优传递矩阵改进层次分析法，利用自调节方法构建比较矩阵，构建完成后转化成一致性矩阵，计算得出权重。具体步骤如下：

确定各层指标间重要性程度，获得3标度比较矩阵：

(6)

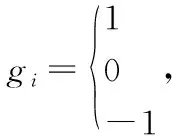
以上比较矩阵可能并不能符合思维判断一致性，通过最优传递矩阵概念，改造矩阵G，求出一致性矩阵和最优矩阵，保证结果符合一致性要求[10]。

通过计算获得比较矩阵G最优传递矩阵：

O=(oij)n*n

(7)

一致性矩阵也被称作判断矩阵，将式(7)最优传递矩阵O转换成判断矩阵Q：

Q=(qij)n*n

(8)

其中，qij=exp{oij}。

经过式(7)与式(8)转换后，判断矩阵Q保持良好的一致性。

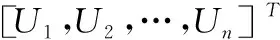
(9)

1.2.6 评价分析

灰色关联度分析依据式(10)实现大学生就业质量综合评价：

R=W*ri

(10)

(11)

判断关联度大小，为各指标排序，关联度值越大评价结果越好。

2 实验结果

将某大学即将毕业的在校大学生作为研究对象，使用本文方法开展实验，所选取的对象为某大学电子类专业的学生，2个班共计102人，使用问卷调查形式收集相关数据，这些参加实验的大学生通过微博、微信等通信方式共填写1 142份问卷，经整理获得522份有效数据，分析整理这些数据，从多个指标评价大学生就业质量。使用本文方法计算各个指标的关联度，统计结果见图2。从图2能够看出，各个指标关联度均高于0.46，说明本文方法评价各指标具有较强的关联度，由此可以看出本文设定的12个评价指标体系可以作为评价大学生就业质量的评价的指标体系，其中C11、C12、C14的关联度值较高，说明这3个指标对评价大学生就业质量存在较高影响[12]，因此可以从这3个方面对大学生就业制定相应调整政策。

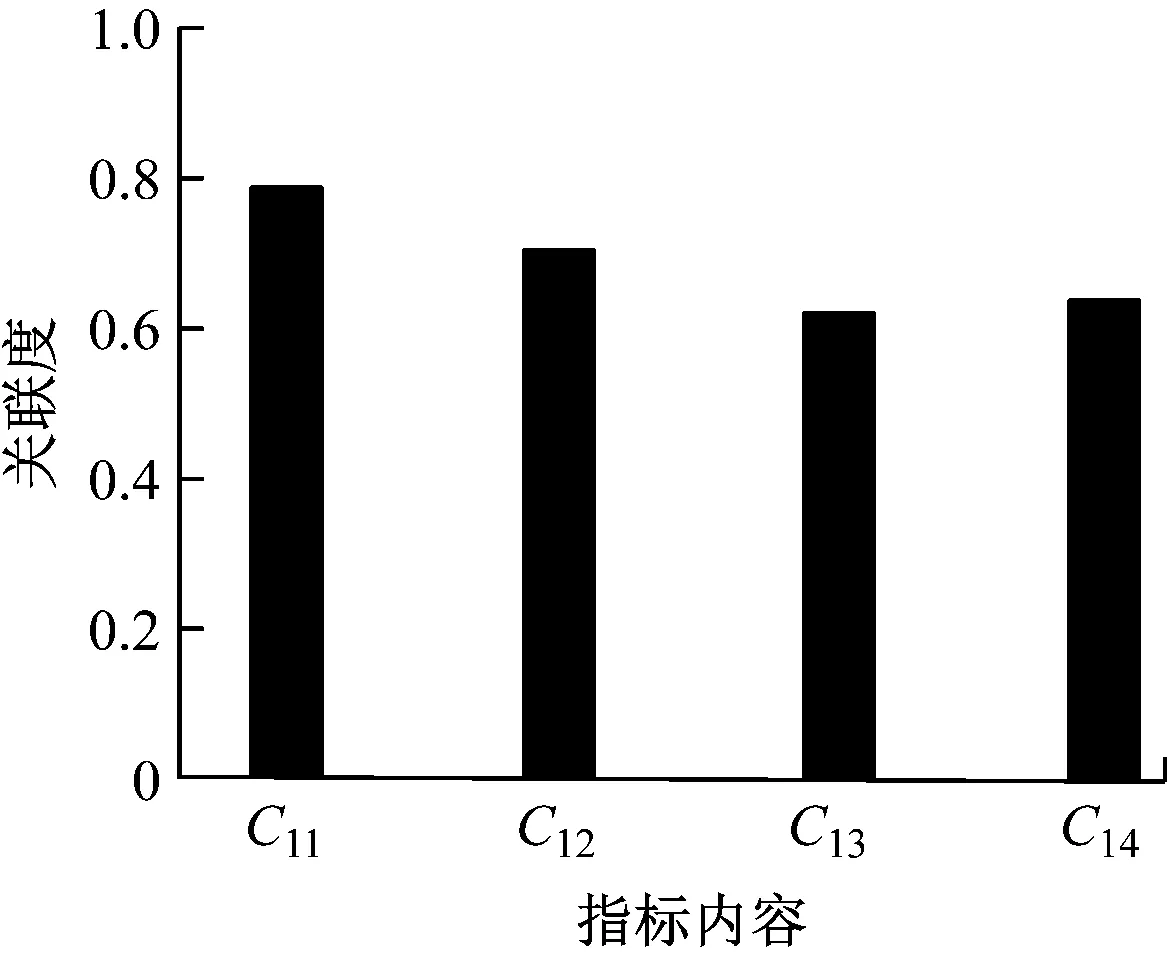
(a) 个人就业质量评价关联度

使用本文方法计算各个指标的权重，统计结果见图3。

从图3可知，使用本文方法能够准确获得各指标的权重，总体来看，各指标权重在0.130至0.011之间波动。

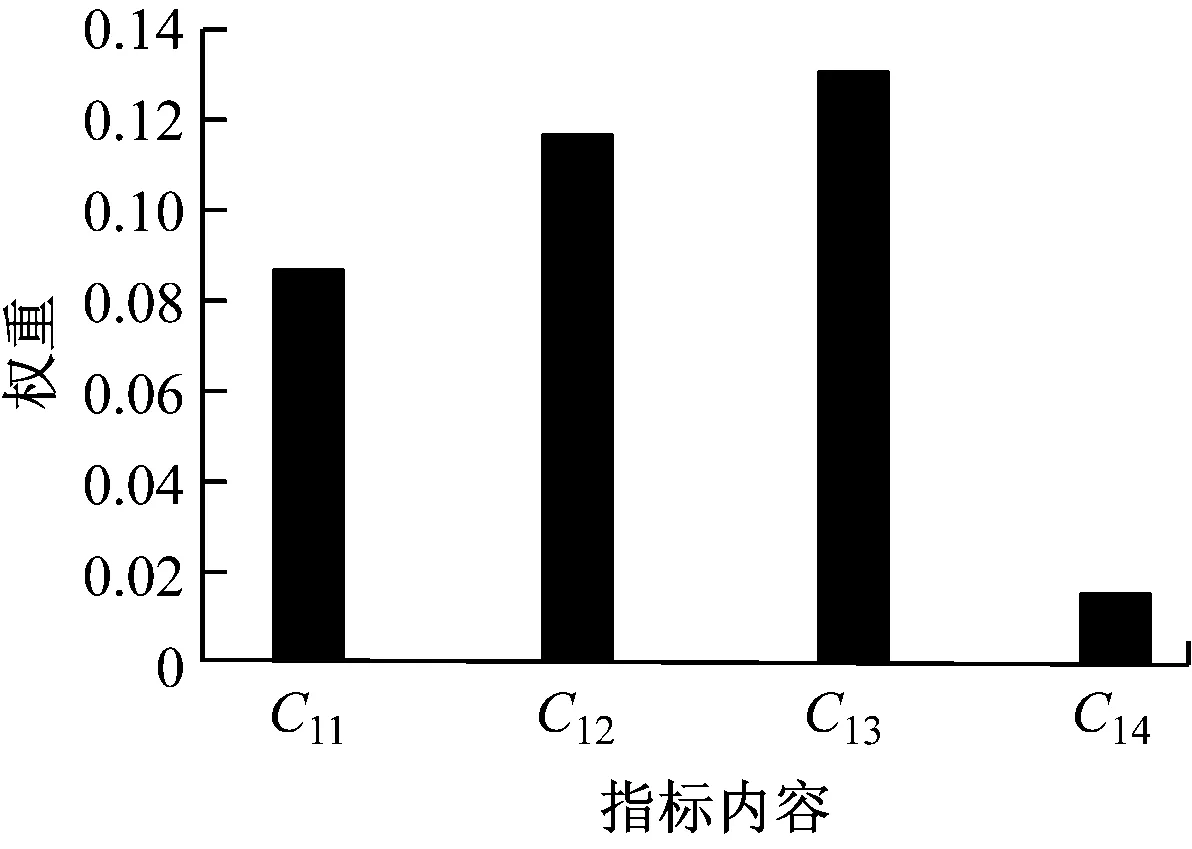
(a) 个人就业质量评价权重

从实验对象中随机抽取100位学生，并随机分为10组，根据评价指标权重和指标关联度，使用式(10)获得计算评价值结果(图4)。为验证评价结果的准确性，邀请专家评分，其中按照指标情况划分出5个等级，评分结果由高至低分别为5、4、3、2、1。

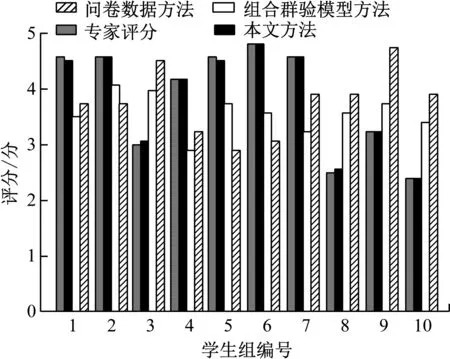
图4 就业质量评价结果

为使实验结果具有对比性，同时使用基于个体问卷数据的评价方法和基于组合群验模型的评价方法对实验中的10组大学生就业质量实行评价，这2个对比结果分别来自文献[7]和文献[8]。

从图4能够看出，本文方法在对大学生就业质量评价的过程中，能够有效得出质量评价结果，且评价的结果与专家实际评分结果较为一致，最大误差保持在0.2分以内，具有较为精准的评价性能。其他方法的评价结果误差较大，组合群验模型方法和问卷数据方法的评分结果误差最大分别达到了1.2分和1.8分，难以准确体现大学生就业质量。这是因为本文方法采用了灰色关联分析方法，对评价指标与就业质量的关联度进行了计算，能够准确反映各指标与就业质量的真实关联信息，从而准确体现了大学生的就业质量结果。

3 总结

大学生就业质量关系高校未来的发展和社会人才的储备对评价大学生就业质量具有深远的影响。本文研究基于灰色关联分析的大学生就业质量评价，使用灰色关联分析法确定参考数据列，运行无量纲化处理数据使其具有规范化，改进灰色关联分析法，结合层次分析法确认权重，实现大学生就业质量评估。评估大学生就业质量时存在诸多影响因素，且各指标之间的关联性不清、定量不明确，灰色关联分析能够极好地解决信息不明确的灰色问题，提高评估的准确性。经实验分析，本文评价方法计算过程简单，能够准确获得各指标关联度和权重，评价结果具有较高准确性，存在较高定量化程度，为评估大学生就业质量提供了一种新的途径。