SARIMA模型和LSTM神经网络在预测深圳市宝安区手足口病疫情中的应用

陈春艳，陈亿雄，赵执扬，李 静，李淑珍*

(1山西医科大学公共卫生学院流行病学教研室，太原 030001；2深圳市宝安区疾病预防控制中心传防科；*通讯作者,E-mail:lszlym@163.com)

手足口病(hand-foot-mouth disease, HFMD)是由多种肠道病毒感染引起的常见急性传染病，常见于5岁以下儿童[1]。临床上以手、足和口腔等部位出现疱疹、斑丘疹为主要症状[2]。多数患者症状较轻，可自愈，少数重症患者可出现中枢神经系统和/或心血管系统并发症如肺循环衰竭、脑膜炎等[3]，甚至死亡。手足口病传播途径复杂、防控难度大，我国于2008年将其列为法定报告的丙类传染病[4]。

时间序列分析[5]是将某种现象某一个统计指标在不同时间上的各个数值，按时间先后顺序排列而形成的序列，旨在预测未来事件发展的趋势和规律，现已被各领域广泛应用。时间序列分析中的季节性差分自回归移动平均模型(seasonal autoregressive integrated moving average model, SARIMA)能够分析发病数据的趋势性、季节性、周期性以及随机性的波动，最常用于预测疾病的发生及发展规律[6,7]，但SARIMA模型要求其时间序列服从平稳性，当序列不平稳时往往需要通过差分等方法将其变为平稳序列，因此会损失一定的信息造成预测准确性降低。近年来，随着深度学习理论的出现和数值计算能力的提升，基于循环神经网络(recurrent neural networks, RNN)改进的一种算法即长短时记忆神经网络(long short term memory, LSTM)逐渐成为时间序列的分析方法之一[8,9]。

广东省深圳市是手足口病的高发城市[10,11]。宝安区是深圳市人口数最多的区，达447万人[12]，是深圳市手足口病的高发地区[13]。因为受新冠疫情的影响，2020—2021年通过“中国疾病预防控制信息系统”报告的深圳市宝安区的HFMD发病数与往年相比，数据质量稳定性受到影响，容易导致构建的模型具有较大的预测误差。为减少误差，本文选取2009年1月至2019年12月深圳市宝安区的HFMD发病数据资料进行研究。通过应用SARIMA模型和LSTM神经网络构建深圳市宝安区手足口病时间序列模型，预测发病趋势，为今后HFMD的预防和控制提供理论依据。

1 资料与方法

1.1 一般资料

2009年1月至2019年12月深圳市宝安区人口数资料来源于深圳市宝安区统计局，2009年1月至2019年12月深圳市宝安区手足口病发病数据来源于“中国疾病预防控制信息系统”。本研究以2009年1月至2018年12月的HFMD月发病率作为训练集分别构建SARIMA模型和LSTM神经网络，预测2019年1—12月的HFMD月发病率。

1.2 研究方法

1.2.1 SARIMA模型 由于手足口病具有季节性波动，本研究构建季节性差分自回归移动平均模型(seasonal autoregressive integrated moving average model, SARIMA)，即SARIMA(p，d，q)(P，D，Q)s。构建SARIMA模型的步骤为：首先进行自相关图检验、单位根检验法(augmented dickey-fullert，ADF)判断数据是否平稳(P<0.05代表序列平稳)，若序列不平稳则需差分直至成为平稳序列。随后对该序列进行白噪声检验即Ljung-Box检验，当序列成为非白噪声时，则可构建SARIMA模型。本研究采用Python网格搜索来自动拟合SARIMA模型，根据赤池信息(AIC最小)准则，采用条件最小二乘法估计模型参数，并对模型参数进行统计学检验，选择相对最优模型，通过模型残差白噪声检验判断模型是否拟合成功(Ljung-Box检验中P>0.05，表示残差为白噪声)。

1.2.2 LSTM神经网络 LSTM神经网络是由Hochreiter提出并由Graves改进的一种常见的循环神经网络[14]。一个LSTM单元结构的核心在于它的神经元状态(cell state)。LSTM包括3个门控结构[8]，即“遗忘门”“输入门”和“输出门”。这3种门控结构可选择性地控制信息通过，信息传递顺序为:先输入ht-1、xt和Ct-1，根据sigmoid、tanh函数和下列公式[8]计算ft、it、ot，其中ht-1代表t-1时刻的输出值，xt代表t时刻的输入值，Ct-1代表t-1时刻的单元状态，ft、it、ot分别代表遗忘门状态、输入门状态、输出门状态[15]。

遗忘门状态：ft=σ(Wf·[Ct-1,ht-1,xt]+bf)

输入门状态：it=σ(Wi·[Ct-1,ht-1,xt]+bi)

输出门状态：ot=σ(Wo·[Ct-1,ht-1,xt]+bo)

单元输入状态:

隐藏层输出状态：ht=ot×tanh(Ct)

其中W是权重矩阵，b是偏倚项，σ表示sigmoid函数。

1.3 模型性能评价

运用均方误差(mean squared error, MSE)、均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)比较两种模型对深圳市宝安区HFMD发病趋势的拟合及预测效果。

1.4 统计分析

采用SPSS 22.0软件对数据进行描述性分析，采用χ2检验进行率的比较，检验水准ɑ=0.05；采用python3.10软件分别构建SARIMA模型和LSTM神经网络。

2 结果

2.1 发病率分析

2.1.1 年发病率分析 2009—2019年深圳市宝安区累计报告手足口病82 632例，年均发病率为291.93/10万，2017年(575.34/10万)及2018年(699.84/10万)的HFMD发病率较高(见表1)。

2.1.2 月发病率分析 除2009—2012年外，其他年份的HFMD月发病率均呈现典型的双峰模式。病例从每年的3月开始增多，到第4—7月达到第1个峰值，随后第9—11月达到第2个峰值(见图1)，即多发于夏秋季节，夏季较秋季高发，具有明显的季节性。

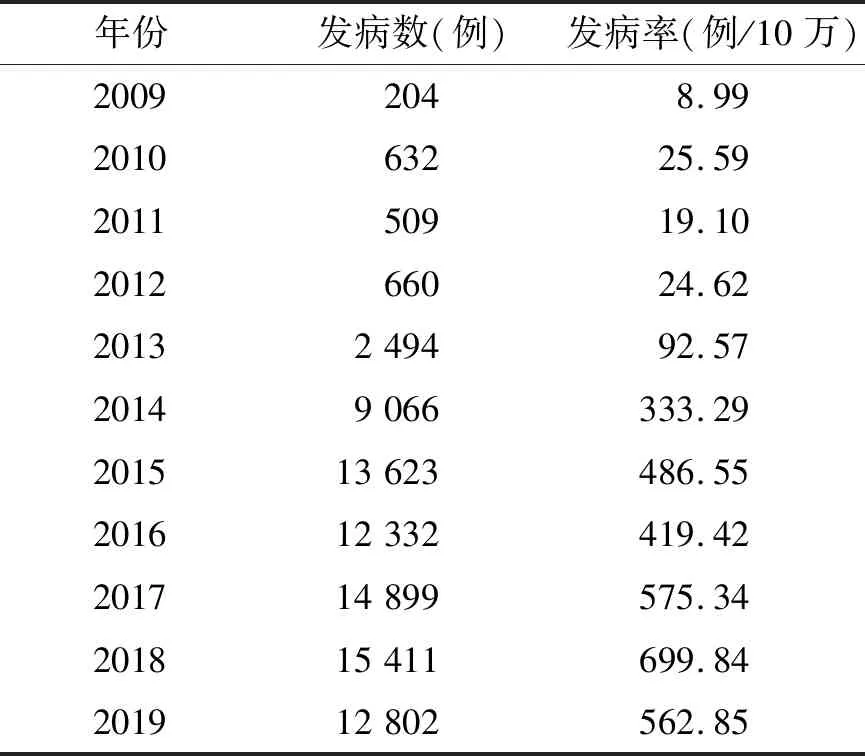
表1 2009—2019年深圳市宝安区手足口病发病的分布Table 1 Distribution of incidence of HFMD in Bao’an district of Shenzhen city in 2009—2019

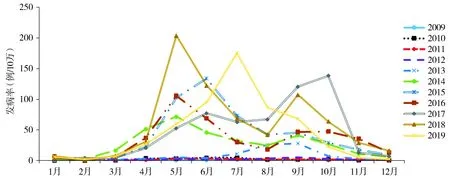
图1 2009—2019年深圳市宝安区手足口病月发病率分布Figure 1 Distribution of monthly incidence of HFMD in Bao’an district of Shenzhen city in 2009—2019

2.2 SARIMA模型

2.2.1 平稳性检验和白噪声检验 对原始序列依次进行平稳性检验和白噪声检验，经ADF检验发现，序列存在单位根(χ2=-0.018，P>0.05，见表2)，对原始序列的自相关图、偏自相关图进行分析，自相关系数超过2倍标准差(见图2)，综合考虑上述结果，认为原始序列为不平稳序列。对序列进行季节性差分得到平稳序列(χ2=-3.091，P<0.05)，随后对该序列进行Ljung-Box检验，序列满足非白噪声要求(χ2=15.841，P<0.05，见表2)。

2.2.2 模型优化 根据序列的差分次数确定非季节性与季节性差分的值，即d为0，D为1，初步选用SARIMA(p，0，q)(P，1，Q)12模型。根据既往文献经验[16]p、q、P及Q取值范围为0～2，采用Python网格搜索自动拟合SARIMA模型，根据AIC最小原则和解释变量尽可能有意义，最终选择SARIMA(0，0，2)(0，1，2)12为相对最优模型(AIC=752.094，BIC=764.066)，对模型的残差序列进行Ljung-Box检验，结果为白噪声(P=0.510，见表3)，说明该模型数据提取完全，效果满意。

表2 序列的平稳性及白噪声检验Table 2 Stationarity of sequences and Ljung-Box test

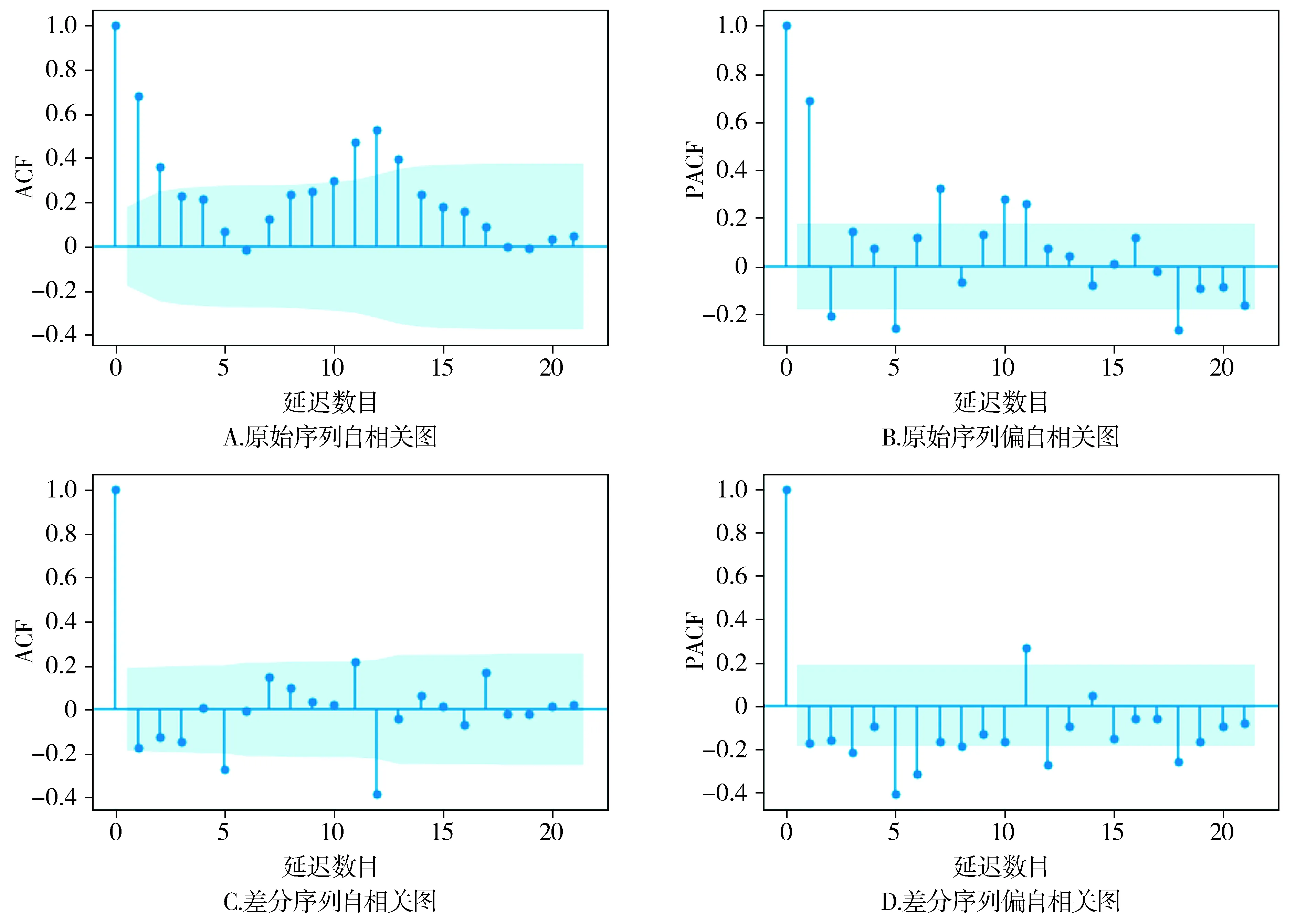
图2 原始序列及差分序列的自相关图与偏自相关图Figure 2 ACF and PACF of original sequence and difference sequence

表3 SARIMA(0，0，2)(0，1，2)12模型参数估计和拟合优度统计量结果Table 3 Parameter estimation and goodness-of-fit statistics for SARIMA(0，0，2)(0，1，2)12 models

2.3 LSTM神经网络

因为手足口病的数据周期为12个月，因此LSTM神经网络的窗口长度设置为12，即输入层节点数为12，预测下个月手足口病发病率，输出层节点数为1。

本文在单隐层的结构下以隐藏层节点数为2的幂次方进行试验，当隐藏层节点数为1 024时，模型的RMSE、MAE、MSE 3个评价指标均最小(见表4)。

固定隐藏层节点数为1 024，设置隐藏层层数为1～5逐个进行试验，结果见表5。当隐藏层层数设置为1时，LSTM神经网络的误差值均最低。

综上，本文设置时间步长为12、隐藏层层数为1、隐藏层节点数为1 024、迭代次数为50时，构建LSTM神经网络。

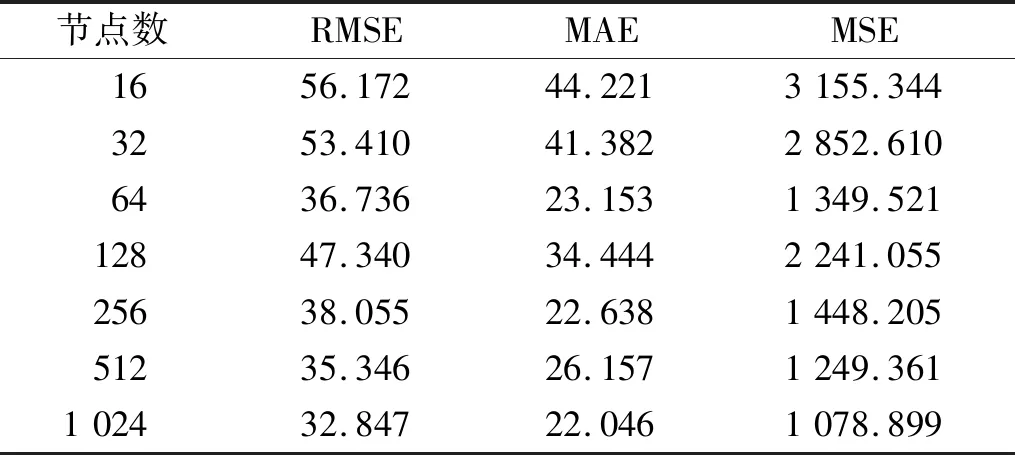
表4 隐藏层节点数对模型预测性能的影响Table 4 The influence of the number of hidden layer nodes on the prediction performance of the model

2.4 两种模型拟合及预测深圳市宝安区HFMD发病的效果评价

在本研究中，采用SARIMA(0，0，2)(0，1，2)12和LSTM神经网络分别对2010年1月至2018年12月深圳市宝安区的HFMD月发病率进行拟合。两种模型对2019年1—12月深圳市宝安区的HFMD月发病率进行预测，SARIMA的预测值出现了双峰分布，而LSTM的预测值呈单峰分布且与实际月发病率基本吻合(见图3)。

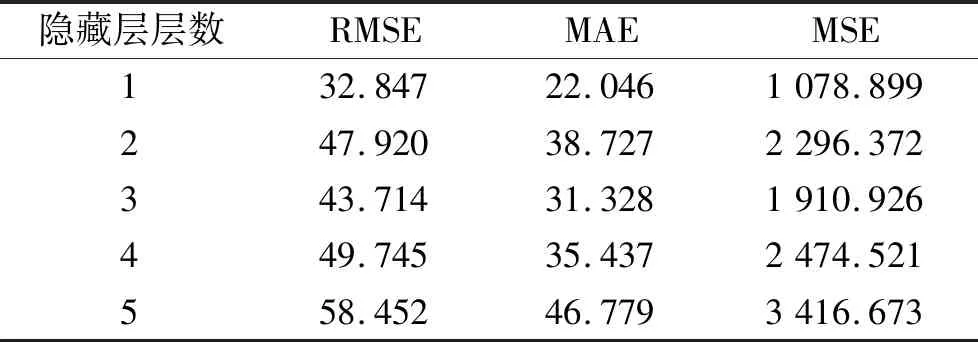
表5 隐藏层层数对模型预测性能的影响Table 5 The influence of the number of hidden layers on the prediction performance of the model

为客观评价模型拟合及预测性能，使用MSE、RMSE、MAE及MAPE对两模型进行比较，在拟合性能中LSTM模型的MSE、RMSE均高于SARIMA模型，而MAE、MAPE均低于SARIMA模型(见表6)，表明两种模型的拟合性能基本一致；而在预测性能中LSTM模型的MSE、RMSE、MAE及MAPE 4个指标均低于SARIMA模型。因此，LSTM神经网络的预测性能高于SARIMA模型，表明LSTM神经网络能更好地预测深圳市宝安区HFMD发病趋势。

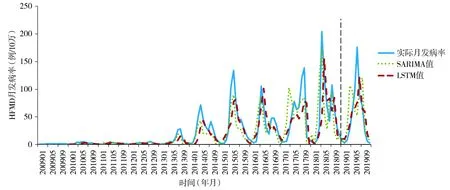
黑色虚线左侧为两种模型的拟合效果，右侧为两种模型的预测效果图3 SARIMA和LSTM模型对2010年1月至2018年12月深圳市宝安区的HFMD月发病率拟合及预测效果的比较Figure 3 Comparison of the performance of fitting and predicting monthly incidence rate of HFMD in Bao’an district of Shenzhen city in 2010—2018 between SARIMA model and LSTM model

表6 两种模型的拟合及预测性能的误差值对比Table 6 Comparison of fitting and prediction errors between the two models

3 讨论

自2008年我国将手足口病纳入丙类传染病管理以来，手足口病的发病率一直位于我国丙类传染病的首位[17]。手足口病是由不同肠道病毒感染所致，不同病原体之间存在差异，易在托幼机构及学校呈暴发流行，这类聚集性疫情的发生给国家和地区的卫生保健系统造成较大的经济负担[18]。本研究中，深圳市宝安区2014—2019年手足口病发病率显著高于2009—2013年，可能原因跟该地区传染病疫情监测系统逐渐完善、外来人口数增多、人口流动性强等密切相关。因此，了解手足口病流行趋势，构建恰当的手足口病预测模型，可为相关部门制定手足口病防控策略提供科学依据。

本研究构建SARIMA模型时，先对原始序列进行平稳性及白噪声检验，判断原始序列是否满足平稳非白噪声，其次观察序列的ACF、PACF图确定模型的参数范围，通过Python网格搜索自动拟合较佳参数，最后运用AIC最小原则，选取了SARIMA(0，0，2)(0，1，2)12为相对最优模型。用该模型分别对深圳市宝安区的HFMD月发病率进行拟合及预测时，误差指数较小，拟合及预测原始序列的趋势性和周期性的效果较好，表明SARIMA模型预测深圳市宝安区HFMD发病趋势的效果尚佳，与韩玲等[19]使用河北省HFMD发病数建立SARIMA(1，1，1)(0，1，1)12模型、刘涛等[20]使用山东省HFMD发病数建立SARIMA(1，0，1)(0，1，0)12模型的研究结果一致。

本研究对LSTM神经网络的隐藏层层数及节点数进行了参数的调整，设置时间步长为12、隐藏层层数为1、隐藏层节点数为1 024、迭代次数为50时构建的LSTM神经网络为较优模型，该模型对深圳市宝安区HFMD月发病率的拟合及预测性能较好，与冯一平等[21]研究认为LSTM神经网络能较好地预测HFMD发病一致。但是，选择最佳参数构建最优LSTM神经网络较难实现，即使部分参数可以根据数据及疾病特征进行大致估计，但构建最佳模型的几率仍然较小，后续将进一步深入研究该问题。

本文中SARIMA模型预测性能的MSE、RMSE、MAE、MAPE均大于LSTM神经网络，可能原因[22]在于构建SARIMA模型的前提是要求原始序列平稳，当原始序列不平稳时，需要进行差分直至成为平稳非白噪声序列，导致SARIMA模型对HFMD发病数据提取不充分，故造成信息利用不充分而产生预测误差，而LSTM神经网络对数据本身是否平稳并无要求，并且其对长期的序列具有较好的预测效果[23]。本研究表明LSTM神经网络能更好地预测深圳市宝安区HFMD发病趋势，与高秋菊等[24]预测石家庄市HFMD发病趋势的研究结果一致。但本文存在一定的局限性，手足口病发病易受多种因素影响，本文仅使用了手足口病监测资料，在后续构建模型过程中应纳入影响手足口病的其他因素，进一步提高模型的准确度，进而提高手足口病发病预测的效果，为手足口病的防控提供更可靠的理论依据。