基于BP神经网络的围岩质量分类研究

刘学军，高玉峰，贺一凡，姜兆东

(1.新疆建筑科学研究院(有限责任公司)，新疆乌鲁木齐830002；2.新疆大学建筑工程学院，新疆乌鲁木齐830046)

0 引 言

隧道工程是交通运输工程的重要组成部分，受地质灾害的影响，在施工过程中经常发生安全问题，甚至会威胁到工程的安全稳定[1]。对隧道围岩的稳定性提前预测可以减少工程事故的发生[2]。针对围岩稳定性的问题，国内外学者已开展了大量研究工作。许传华等[3]采用模糊数学综合评估法和模糊语言等计算方法，对围岩稳定性进行了不同程度的评估。曾怀宇[4]为分析地质水文环境及岩石自身条件等众多因素对围岩分类的影响，在已收集数据的基础上，采用粗糙集理论对数据中的隐含知识进行挖掘，实现对隧道围岩等级的预判。储汉东等[5]进行数值模拟，研究围岩的应力和应变变化场。李健等[6]基于云模型理论探讨了围岩稳定性分类模型。闫天俊等[7]对弱结构面流动修正系数进行修正，并提出了考虑到岩石流动影响的围岩分类指标。郝杰等[8]通过使用基于拓扑元素理论的简单相关函数，确定影响围岩的每个因素的权重。王佳信等[9]提出一种基于Alpha稳定分析(SaS)-概率神经网络(PNN)模型，对围岩稳定性进行了预测。贡力等[10]为对围岩的安全稳定性做出准确预测，提出了基于PCA-IRBF的计算模型，对隧道围岩的安全稳定性进行预测评价的新方法。李宏波[11]为探究TBM掘进量围岩等级关系，采用数据清洗、分布统计等多种方法，建立了以神经网络聚类和最小二乘支持向量机相结合的围岩等级预测方法。周浩宇等[12]以江西某隧道为例，根据已有工程经验，选取合适的影响因素建立指标体系，采用理想点法建立隧道坍塌风险等级预测模型。李蓬喜[13]采用支持向量回归、卷积神经网络工智能算法，对TBM的掘进数据、围岩等级进行预测分析。

在东天山隧道施工研究中，秦拥军等[2]利用TSP物探技术与灰色关联度等技术对东天山隧道施工前期的数据进行了分析，并对围岩质量进行预测研究，但其研究是基于东天山隧道施工前期的数据，数据量较少导致其研究成果仍存在不足。为此，本文在秦拥军等人研究的基础上，采用东天山隧道施工后期的数据进行研究分析，所得数据更加完备，监测数据更为丰富，可使研究结果更加准确可靠。此外，在实际工程中获取的数据往往是庞大的，需要找到一个可以大规模处理工程数据的方法。随着人工智能的不断发展，具有大规模并行处理、高运算速度、强适应性以及强容错能力等高性能的神经网络被广泛应用。鉴于以上原因，本文基于优化后的东天山隧道施工后期数据，利用高性能的神经网络等处理技术，对围岩隧道质量进行预测。

1 工程概况

新疆东天山隧道全长约11 km，位于高山区和中山区，融雪和降雨等因素易地表形成径流。受多时期构造运动的影响，导致项目沿线出露的基岩节理较为发育[14]。隧道地理位置见图1。

图1 隧道地理位置

根据现场踏勘与钻探取样分析，隧址区上部主要为粉质黏土、卵石和块石等，属于第四系全新统～上更新统；隧址区下部基岩岩性主要为凝灰质砂岩、凝灰岩、熔结泥灰岩和花岗岩、辉绿岩、花岗斑岩等，属于石炭系中统及华力西期侵入岩。东天山隧道主要跨越了2个三级构造单元，走向为北西～北西西的区域构造占了绝大部分，走向为北东或近南北的仅有极少部分。北天山北坡陡、南坡缓，北部冲洪积扇较南部山麓发育，南部新构造活动明显弱于北部。

2 基本理论分析

2.1 主成分分析关联理论

主成分分析是用1组新的相互不相关的综合指标替代大量的指标(如P指数)。当统计分析被用来研究1个多变量的课题时，太多的变量会增加课题的复杂性，希望以较少的变量获得更多的信息。在存在多因素影响的条件下，多变量之间存在内在的联系。如果2个变量之间有内在关联，则认为这2个变量反映的主体信息有一定的重叠。主成分分析是将重复的变量(密切相关的变量)从最初提出的所有变量中删除，并创建尽可能少的新变量，使这些新变量是2个或更多的不相关的变量，这些新变量在反映被试的信息能尽可能多地保留原有信息。

最经典的方法是用F1的方差来表示。若全部组合中的F1方差最高，则F1称为第1主成分。假如F1难以反映原始指标P的信息，再考虑F2，使其有效地代表原始信息。同时，F2中的信息不再包括F1中的信息。也可以表达为要求Cov(F1，F2)=0，则将F2称为第2主成分。以此类推可以构造第i个直至第P个主成分[15]。

2.2 TSP物探指标敏感性分析

考虑岩石硬度和岩石完整性2个基本因素的质量特征，以及基本的围岩质量指标BQ进行初步分类[16]。基本质量指数的修正值是考虑到修正因素的影响而得到的。岩体的基本围岩质量指标BQ的计算公式为

BQ=100+3Rc+250Kr

(1)

式中，RC为岩石单轴抗压强度；Kr为岩石完整度系数。若RC>90Kr+30，则将RC=90Kr+30和Kr代入计算BQ值；当Kr>0.04Rc+0.4时，应以Kr=0.04Rc+0.4和Rc代入计算BQ值。

计算出BQ值后，结合JTG 3370.1—2018《公路隧道设计规范》给出的地下水影响修正系数K1、主要软弱结构面产状影响修正系数K2、初始应力状态影响修正系数K3进行修正计算得出围岩质量指标修正值[BQ]，计算公式为

[BQ]=BQ-100(K1+K2+K3)

(2)

就东天山隧道而言，工程条件复杂，在隧道的长段上，干燥和水淹的条件交替出现，而且结构的表面几何形状也不同。仅采用3个修正条件难以全部满足所有条件，同时修正系数的取值将受到影响，导致计算出的[BQ]修正值存在误差。对地下水修正系数K1进行加权平均计算，可以使得结果更加准确[17]，计算公式为

(3)

式中，ki为第i个因子的地下水修正系数；wi为第i个因子的隧道长度；n为因子个数。

例如，假设一段巷道长200 m，岩体基本围岩质量指标BQ为330，其中有55 m是潮湿或点滴状出水，且水压小于0.1 MPa；有145 m是淋雨状或涌流状出水，其中有105 m水压大于0.5 MPa，有40 m水压大于0.1 MP且小于等于0.5 MPa。如果按规范计算，200 m中有105 m为淋雨状或涌流状出水且水压大于0.5 MPa，则地下水修正系数K1的取值为0.8，这样计算出来的修正值[BQ]会比实际偏低。若采用加权平均法，则

3 研究数据处理

3.1 加权修正围岩质量指标

在秦拥军等[2]研究的基础上，采用东天山隧道施工后期优化后的数据进行研究分析，计算出[BQ]值，并列出相应的TSP物探指标。由于数据过多，因此只列出表1所示的部分主要数据。

3.2 关联度计算结果

将表1的数据通过MATLAB编程进行关联度计算，结果见表2。通过TSP物探指标敏感性分析可知，在多因素物理力学参数的影响中，波速V、纵横波速比Vp/Vs、泊松比μ和密度ρ与围岩质量的相关程度较高，所以可以认为这4个因素是影响岩石质量及稳定性的主控因素。而剪切模量G、拉梅系数L、体积模量K、动态杨氏模量ED和静态杨氏模量ES与围岩质量的相关程度最低，说明这5个因素对围岩质量及稳定性影响相对较小。

表1 东天山隧道TSP物探指标及对应[BQ]值

表2 TSP物探各指标的围岩稳定性关联系数

4 BP神经网络预测围岩质量

4.1 BP神经网络关联理论

BP算法是神经网络众多算法中较为经典的算法，同时也是应用最广泛的算法之一。BP算法搭建的神经网络主要由输入层、隐含层和输出层3层神经元构成，3层全部存在情况下，将其称为全连接神经网络，见图2。

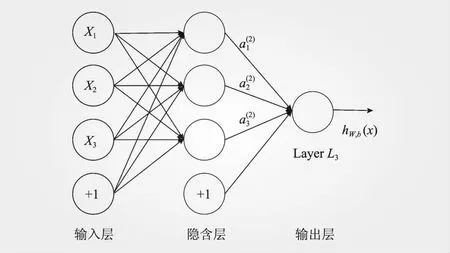
图2 全连接神经网络结构

全连接神经网路中，输入层和输出层一般为单层神经元，而隐含层通常为双层甚至多层神经元。神经网络的输入层主要负责提取样本数据，并将数据传递给隐含层做深层处理，最终将处理好的数据传递给输出层，而神经网络模型的准确与否，通常由隐含层来决定。神经网络中处理数据的方法采用BP算法，通过比对神经网络的实际输出与期望输出，降低两者误差。经过对神经网络结构及参数的大量调试，当误差在允许范围时，则认为神经网络已经训练完成。

4.2 预测数据处理

由表2计算得出的结果，选取V、Vp/Vs、μ和ρ这4主控因素作为隧道围岩质量预测的主要依据。预测样本采用表1中随机选取的6组数据(见表3)，初始数据为剩余的512组数据(见表4)，所取数据是在文献[2]的基础上进行优化，数据的来源是隧道工程施工后期，且取样的部位更加合理，因此本文所用数据更有代表性。在初始数据与预测样本的关联度计算中，本文使用灰色关联算法计算。在512个初始数据计算出的关联度中选取最大关联度所对应的初始数据的围岩质量，作为该组预测样本的结果。

表3 预测样本(参考序列)

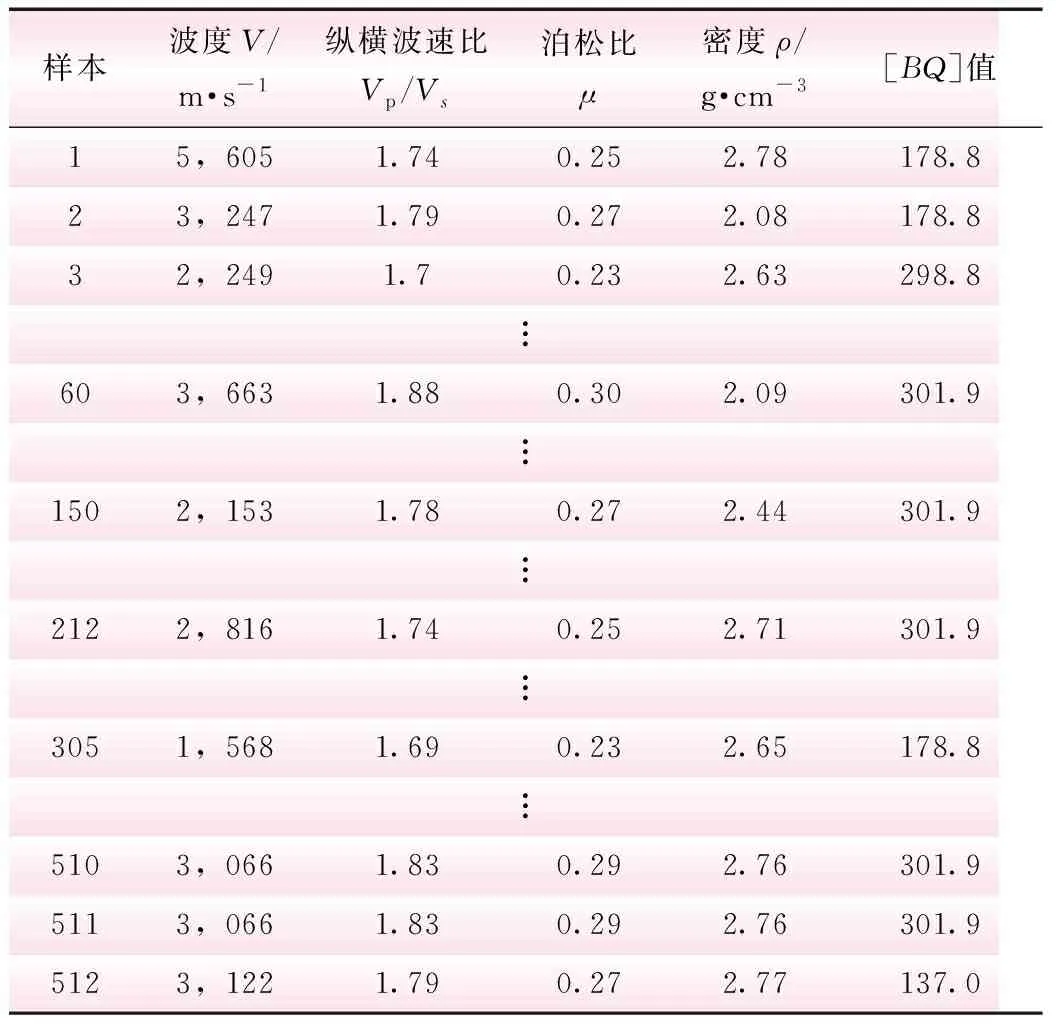
表4 初始数据(比较序列)

4.3 预测结果

采用BP神经网络预测计算得出的结果见表5。

从表5可以看出，除预测样本6外，所有5组预测样本都可以在表4的512组试样中找到对应的实际样本数据。此外，由于工程数据的不完整性，导致预测样本2的预测结果存在误差，但误差在允许范围内。从整体数据来看，[BQ]值为131.8的数据总量较少，这是误差产生的主要原因之一。随着工程数据的不断增加和完善，BP神经网络的预测精度将会越来越高。因此，利用地球物探指标的高度相关性预测围岩质量是可行的。

表5 样本的BP神经网络关联度预测结果

5 结 语

本文以新疆东天山隧道工程为研究对象，利用施工后期优化后的数据，采用TSP物探指标敏感性分析法和BP神经网络关联分析理论，对影响隧道围岩质量的因素进行分析，并对围岩质量进行预测，所得结论如下：

(1)TSP物探指标敏感性分析结果表明，V、Vp/Vs、μ和ρ与围岩质量的相关性最高，关联度分别高达0.802 7，0.863 3，0.855 7和0.819 4，均是影响围岩质量的重要因素。

(2)根据BP神经网络对围岩质量主要影响因素的预测结果可知，BP神经网络预测方法是可靠准确的，所得结果将会随着技术和数据的完善而有所改善。

(3)围岩的纵横波速比和泊松比的预测精度对TSP物探指标预测结果影响较大，提高2个因素的预测精度可有效增强整体预测效果。