针对动态障碍物的7R机械臂实时避障方法
赵 京, 李世龙, 龚世秋
(北京工业大学材料与制造学部, 北京 100124)
随着机器人的应用范围越来越广,冗余机械臂凭其在避障、避奇异、避极限、关节容错等方面突出的性能,成为当前研究的热点[1].
避障路径规划是冗余机械臂控制的基本问题之一[2-3],目前常用的冗余机械臂动态避障算法主要为人工势场法和梯度投影法. 人工势场法凭借其算法简单、适应动态障碍以及不需要逆运动学求解的独特优势得到广泛研究[4],针对其算法本身具有局部最小解、目标不可达等问题,已经有许多学者进行了相关的改进扩展研究,如针对移动式机械臂的路径规划问题[5],通过修改势能函数绕开局部极小点[6]等. 梯度投影法能够在保证末端位姿约束的前提下,利用零空间矩阵映射将避障速度映射到冗余机械臂的自运动中[7],在避障的同时能够良好地体现出机械臂的冗余特性,实现避障次要任务[8].
上述方法在其各自适应的领域取得了良好的避障效果,但却有各自的局限性:梯度投影法,主要用在机械臂末端有具体的任务轨迹约束情况下[9],其避障效果常常因自运动的较小转动幅度而受到限制[10-11];而改进人工势场法,是以引入额外的计算项来解决原算法的缺陷[12-13],其在机械臂的运动控制应用中主要有2个层面:一种是在笛卡儿空间构建引力和斥力,并将合力通过雅可比矩阵转换为对机械臂的速度控制[14],另一种是基于关节邻近空间搜索的不断迭代,对当前关节位形下的所有相邻位形全部进行势能计算以筛选最优解[15],这2种方法都会随着机械臂自由度的增多导致计算量急剧增大,已无法满足在动态障碍物环境下的实时需求.
因此,针对当前广泛采用的七自由度冗余机械臂,以及无末端轨迹约束的条件下,本文通过分析冗余机械臂的结构特点,提出了具有高实时性的避障算法,并通过仿真验证了算法的有效性.
1 避障策略
1.1 避障基本思路
目前,在有障碍物环境下的机器人的规划控制策略有很多种,如通过不同手段以求解运动轨迹的A*、RRT等,或是引入新的评判概念以减小计算量的人工势场、伪距离等. 但无论控制策略的形式如何多样化,其关键过程主要分为2个阶段:1)达点过程中与障碍物的靠近与远离; 2)即将碰撞时的避障规划,如图1所示.
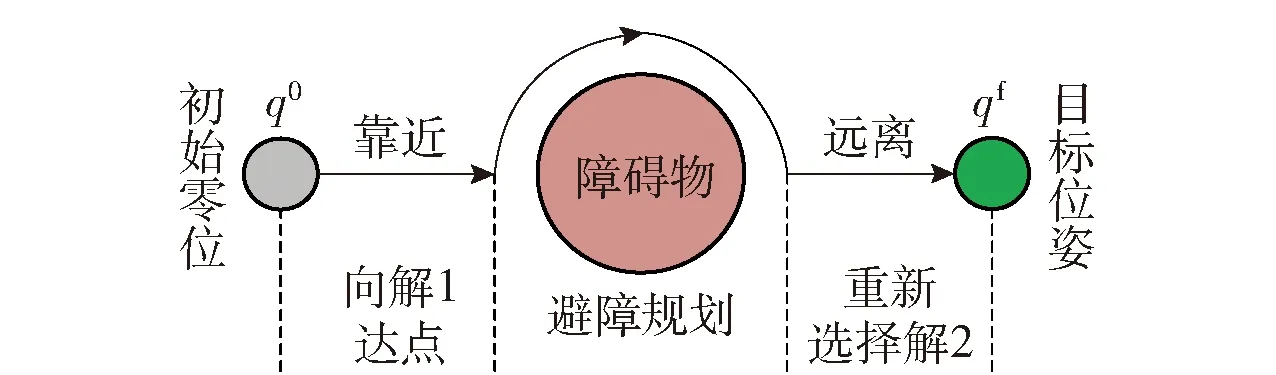
图1 机械臂避障策略Fig.1 Obstacle avoidance strategy of manipulator
本文着手于冗余机械臂在向目标达点运动过程中如何快速避开障碍物. 对于冗余机械臂而言,其末端满足目标位姿的关节位形解有无数种,如何在无数种解中选择一种作为目标关节位形进行达点运动,同时如何在运动过程中即将靠近障碍物时进行避障规划,是本文的主要研究内容.
1.2 7R机械臂模型
本文以常见的七自由度冗余串联正交机械臂为研究对象,其结构及关节配置如图2所示.
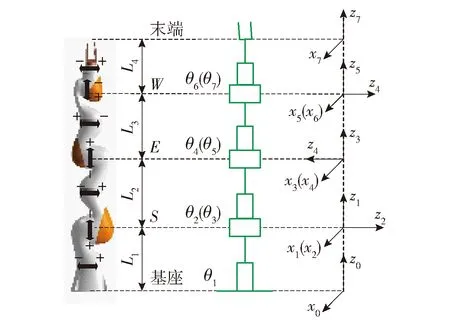
图2 7R机械臂的结构模型Fig.2 Structure model of 7R manipulator
此类型的七自由度机械臂可模仿人手臂结构进行关节布置,θ1、θ2、θ3组合模拟人臂肩关节运动,θ5、θ6、θ7组合模拟腕关节运动,中间θ4模拟肘关节运动. 该构型的机械臂能够在末端位姿保持不变的同时,其肘部E点可以绕肩部S点与腕部W点的连线进行自运动,能够良好地体现出冗余机械臂的冗余特性,如图3所示.

图3 7R机械臂自运动示意图Fig.3 Self motion diagram of 7R manipulator
1.3 达点阶段
在给定了机械臂末端需要达点的目标位姿,关节空间中存在着无数组解,这些不同的解的集合即为满足目标位形的自运动解集. 如何从解集中求得合适的位形解,就需要从这些解的集合中根据条件需求进行选择,按相关指标确定合适的肘部自运动角,即可得到唯一逆解[16].
以自运动角变量φ为输入参数,即可得到对应的关节角度逆解集合Q,再根据目标点、障碍物以及机械臂三者之间的关系,按设定指标即可快速求出解集中的合适逆解,主体表达公式为
Q={q|q=f(R,P,φ),φ∈[0,2π]}
(1)
式中:R、P分别为机械臂末端的姿态矩阵和位置向量;φ为自运动角变量;q为对应自运动角φ的关节逆解向量;Q为对应不同自运动角的q的集合.
1.4 避障阶段
当障碍物靠近机械臂连杆时,将最接近障碍物的杆件设为主要危险杆件,对其进行避障引导. 根据串联机械臂的运动特性分析,其控制方式有2个特点:1)单根连杆的位置和姿态仅由靠近基座一侧(前侧)的多个关节进行耦合控制,而与靠近机械臂末端执行器一侧(后侧)的关节无关,若前侧的关节不变,无论后侧的关节怎么变化,这根连杆的位置和姿态都不会变化,因此要使最近杆远离障碍物仅需对杆件前侧的关节进行控制即可;2)当连杆运动形式以靠近基座的上一根连杆为参照物时,可视为以杆长为半径、两杆连接点为球心的球体运动,如图4所示.

图4 避障的等效控制示意图Fig.4 Equivalent control schematic of avoidance
图4中距障碍物最近杆为L3杆,其相对于L2杆的运动由连杆所在的前2个关节θ3、θ4进行控制,因此通过前2个关节即可对最近杆进行一定程度的运动控制,在求逆解时也具有计算量低的优势.
但是,仅靠控制单一杆件避障会有一定的局限性. 仍以图4所示为例,当障碍物较靠近连接点E时,仅对L3杆控制时无法高效地避开障碍物,无论L3杆如何转动,障碍物距连接点E仍较近,因此结合串联机械臂的控制特点,将对L3杆的避障控制退化到前侧的L2杆上,在对最近杆避障控制的同时,也对靠近基座的上一连杆进行避障控制,从而使机械臂有效地避开障碍物.
2 避障实施算法
2.1 障- 杆距离计算
机械臂在执行操作任务过程中,与障碍物的碰撞检测是进行避障规划的基础. 目前常用的碰撞检测采用线段- 球体包络盒检测:将障碍物用球体包络,同时将机械臂的杆件用圆柱体包络. 对于随机运动的动态障碍物,保证障碍物位置检测的效率尤为重要,传统的在欧式空间的点线距离计算方法在高维机械臂运动过程中,需要对每根连杆构建直线方程,计算量大,且易引起计算误差. 因此本文引入机械臂连杆之间的坐标系转换概念,每根杆件i都有相对于基系的转换矩阵0Ti,将障碍物坐标逆向投影到每根连杆的局部坐标系iPobs(x,y,z)中,以简单的矩阵运算来快速计算障碍物与每根杆件的距离,障碍物在连杆i坐标系下的坐标为
iPobs=(0Ti)-10Pobs
(2)
依据障碍物与杆件的位置关系,可知在连杆坐标系下的杆障位置情况主要有3种,如图5所示.

图5 障碍物在杆件坐标系中的3种位置情况Fig.5 Three positions of obstacles in the rod coordinate
根据不同的位置关系,可快速计算得到障碍物到杆件i的距离di为
(3)
(4)
式中:Li连杆的杆长;robs、rlink分别为障碍物和杆件的包络盒半径;dmin为障碍物到机械臂连杆的最小距离. 当障碍物靠近连杆L1时,由于此杆件固连于基座,关节的转动对于杆障关系没有影响,故此情况条件忽略不予探究. 同时可得到连杆i上与障碍物最近点Pn的坐标.
2.2 单杆件避障
在确定与障碍物最接近的连杆后,根据杆障的几何位置关系,对此连杆进行避障规划.
如图6(a)所示,E-W-末端为机械臂在达点运动过程中的当前位形,Et-Wt-目标位形的末端为从自运动解集中优选出的目标位形,Pobs为障碍物. 此时杆件已无法由当前位形直接运动到目标位形,本文在最近点处引入2个避障向量vavo与vatt,两者共同作用引导此杆件避开障碍物,如图6(b)所示. 图中Pn为连杆上与障碍物最近点,Pt,n为在目标位形上的对应相同点,Pi,1与Pi,2分别为连杆i靠近基座和机械臂末端的2个端点,vavo为垂直躲避分量,其方向垂直于最近点Pn与障碍物Pobs的连线,vatt为吸引分量,沿Pn指向Pt,n,两者表示为
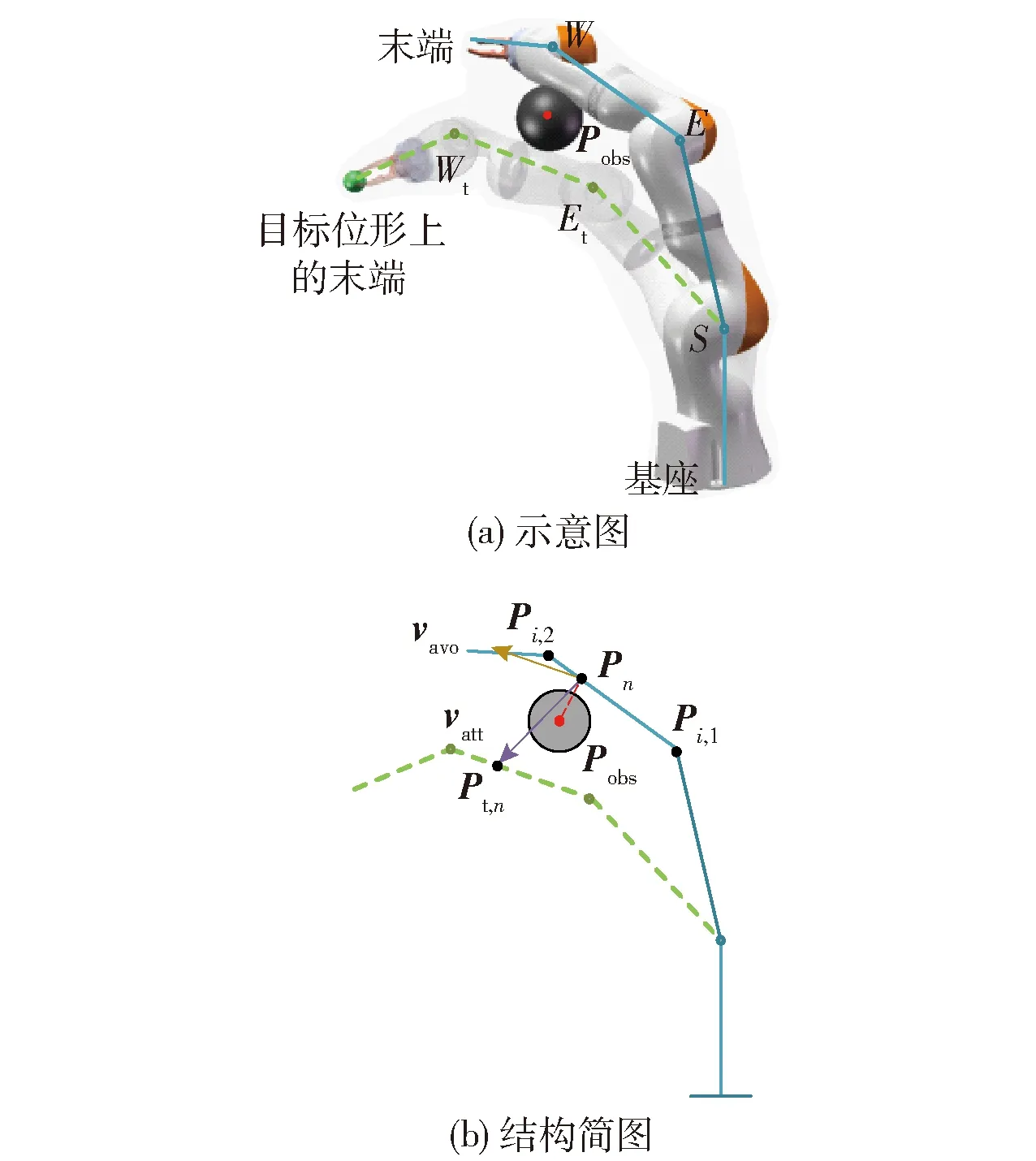
图6 机械臂与障碍物碰撞图Fig.6 Collision diagram of robot arm and obstacle
(5)
式中vavo的默认方向为由点E、W、Pobs三点构成的平面的法线方向,而本文需要其方向为指向远离障碍物的一侧,即在平面的两侧中与点Pt,n相同的一侧,以达到快速避障并达点的效果. 因此,对vavo的方向进行判别并优化,若其方向与点Pt,n在平面不同侧,则避障分量vavo的方向取反,若相同则不变.

(6)
式(6)得到的是标准单位大小的避障引导分量,还需要根据当前位形、障碍物、目标位形三者的位置关系,实时调节两分量的大小.
vs=kθvavo+(1-kθ)vattkθ=(tanh (kθ,1+kθ,2θ)+1)/kθ,3θ=arccos (vPn,Pobsvatt/(‖vPn,Pobs‖‖vatt‖))
(7)
式中:θ为向量vPn,Pobs与vatt的夹角;vs为垂直躲避分量和吸引分量的合向量;kθ为与θ相关的曲线调节权重;kθ,1、kθ,2、kθ,3为相关调节参数.
如图7所示,当θ<π/2时,障碍物位于当前位形和目标位形中间,k趋近于1,垂直躲避分量vavo起主要引导作用,引导机械臂快速避开障碍物;当θ逐渐增大至π时,k由1单调减小至0,分量vatt起主要引导作用,引导机械臂快速脱离障碍物.

图7 等效的机械臂与障碍物Fig.7 Equivalent manipulator and obstacle
机械臂的连杆可视为刚体,杆件上每一点处的运动方向都相同,故最近点Pn处的避障向量可以等效为在杆端Pi,2处的方向相同的避障引导向量. 基于式(5)~(9)得到的避障引导总向量vs为单位向量,还需要引入与杆障最小距离dmin相关的动态调节步长,即
vLi=kdvskd=(1-tanh (kd,1(dmin-dsafe)+kd,2))/kd,3
(8)
式中:vLi为等效的连杆i末端处的避障引导速度;kd为与杆障距离相关的动态调节步长;kd,1、kd,2、kd,3为相关调节参数;dsafe为杆障距离的安全阈值,当dmin>dsafe时,kd=0;当dmin逐渐由dsafe减小至0时,kd由0单调增大至1,避免了在达点运动和避障运动两者间切换时产生的关节速度突变,如图8所示.

图8 避障速度权重的变化趋势Fig.8 Change trend of weight for avoidance speed
根据杆件与关节的构型关系分析,杆件i末端的运动控制可简化为上一连杆i-1的2个关节驱动,这种简化关系可将单根杆件的运动控制视为定长半径的球坐标系控制,如图9所示.
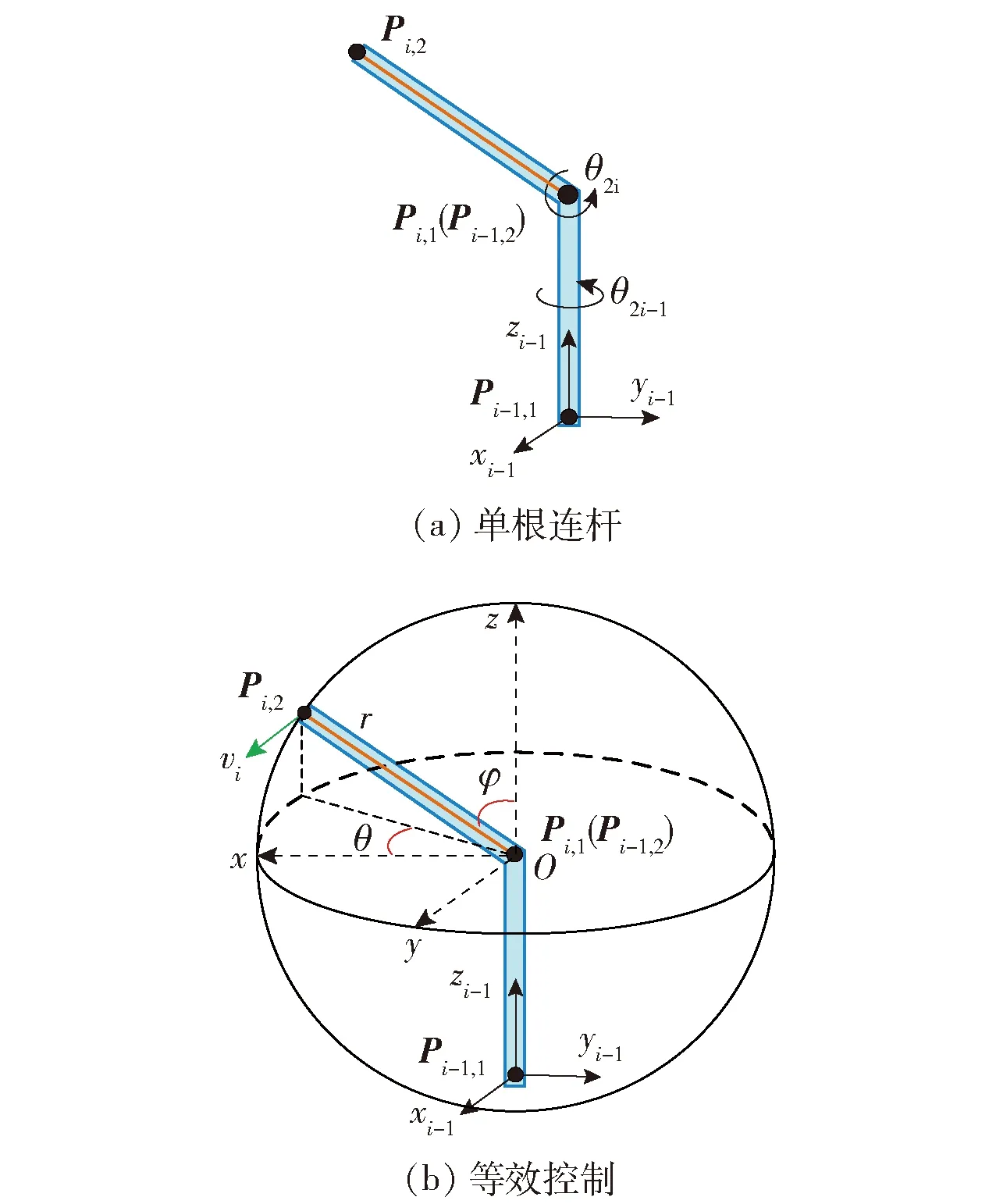
图9 单根连杆的等效控制Fig.9 Equivalent control of single link
连杆i的杆长可视为球坐标系的半径r,上一连杆i-1的2个关节θ2i-1、θ2i可视为球坐标系的两坐标分轴θ、φ.在得到连杆i末端处的引导速度后,可求得对应的关节角变化
i-1PLi,2=(0Ti-1)-1(0Pi,2+vi)
(9)
θ2i=arccos (i-1Pi,2(z)/Li)θ2i-1=arccos (i-1Pi,1(x)/(Lisinθ2i))
(10)
式中i-1Pi,2为连杆i末端在上一连杆i-1的局部坐标系下的位置投影.
2.3 多杆联合避障
仅依靠对单根连杆进行避障控制在某些杆障位置下有一定的局限性,如图10所示.
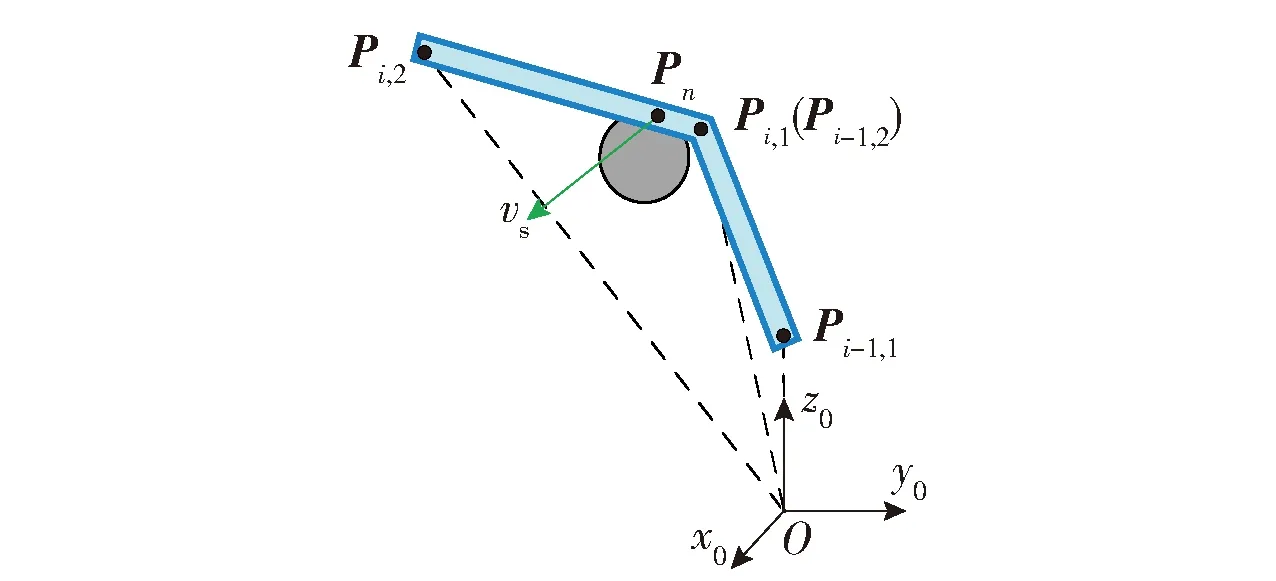
图10 单根连杆规划的局限情况Fig.10 Limitations of single link planning
随着障碍物的位置变化和机械臂的运动,障碍物最近点Pn在连杆i上的位置也不断变化,当其较接近连杆的杆端Pi,1时,尽管避障引导向量vs仍然起效,但连杆需要很大行程的角度才能躲避绕开障碍物,这在实际的运动控制中是不合理的. 因此面对上述情况,根据所确定的主要危险连杆和次要连杆进行联合避障规划.
当最近点Pn接近连杆的杆端Pi,1时,在保留对连杆i规划的同时,将避障引导向量vs退化至上一连杆i-1,对其进行避障引导,并引入改进的Sigmod函数作为权重,平滑最近点Pn在Pi,1与Pi,2两连杆之间运动切换时的抖动,表示为
wd=k1/(1+exp (-k2dPn,Pi,1))-k3
(11)
(12)
式中d为最近点到其所在杆件上一端点的距离,距离越小则当前杆件的关节避障角度变化的权重越小,上一杆件的权重越大. 当d大于一半杆长Li/2时,wd趋近于1,此时对主要危险杆i进行规划引导;当d小于Li/2并大于0时,wd由1单调递减至0,此时同时对主次危险杆i和i-1进行避障规划;当d接近0时,wd=0,此时最近危险杆件已由连杆i转变为i-1,则算法将对连杆i-1和i-2进行规划引导.
2.4 最优解选择
在避开障碍物后,继续向目标关节位形进行达点运动,若此时继续以靠近障碍物之前的目标位形进行达点,可能会出现陷入局部振荡的现象,原因是障碍物与之前选定的目标位形发生了干涉,即上一步规划引导避开了障碍物,下一步进行达点运动时又重复接近障碍物. 因此,在对机械臂避障引导规划完成后,根据此时障碍物与机械臂连杆之间的位置关系,重新在自运动解集Q中选择最优目标解.
参考势场原理,以与当前关节的行程差值最小和到达目标时与障碍物距离最大为优化目的,建立势场函数为
(13)
Ure=kre/(Pφ,E-Pobs)2
(14)
(15)
式中:θnow为当前时刻的关节角位形;Ujoi为当前位形距自运动解集中的不同目标位形的关节行程势能函数;kjoi为相关引力增益参数;Q(φ)n为自运动解集中自运动角为φ所对应的关节位形解;Ure为解集中不同目标位形下与肘关节点E和障碍物之间的距离成反比的排斥势场函数;kre为相关斥力增益调节参数;Pφ,E为自运动角变量为φ时的肘关节端点E在基座标系下的位置. 可计算得到与当前关节位形相距较近,同时又远离障碍物的新的最优目标解θtar.
算法整体流程图如图11所示.
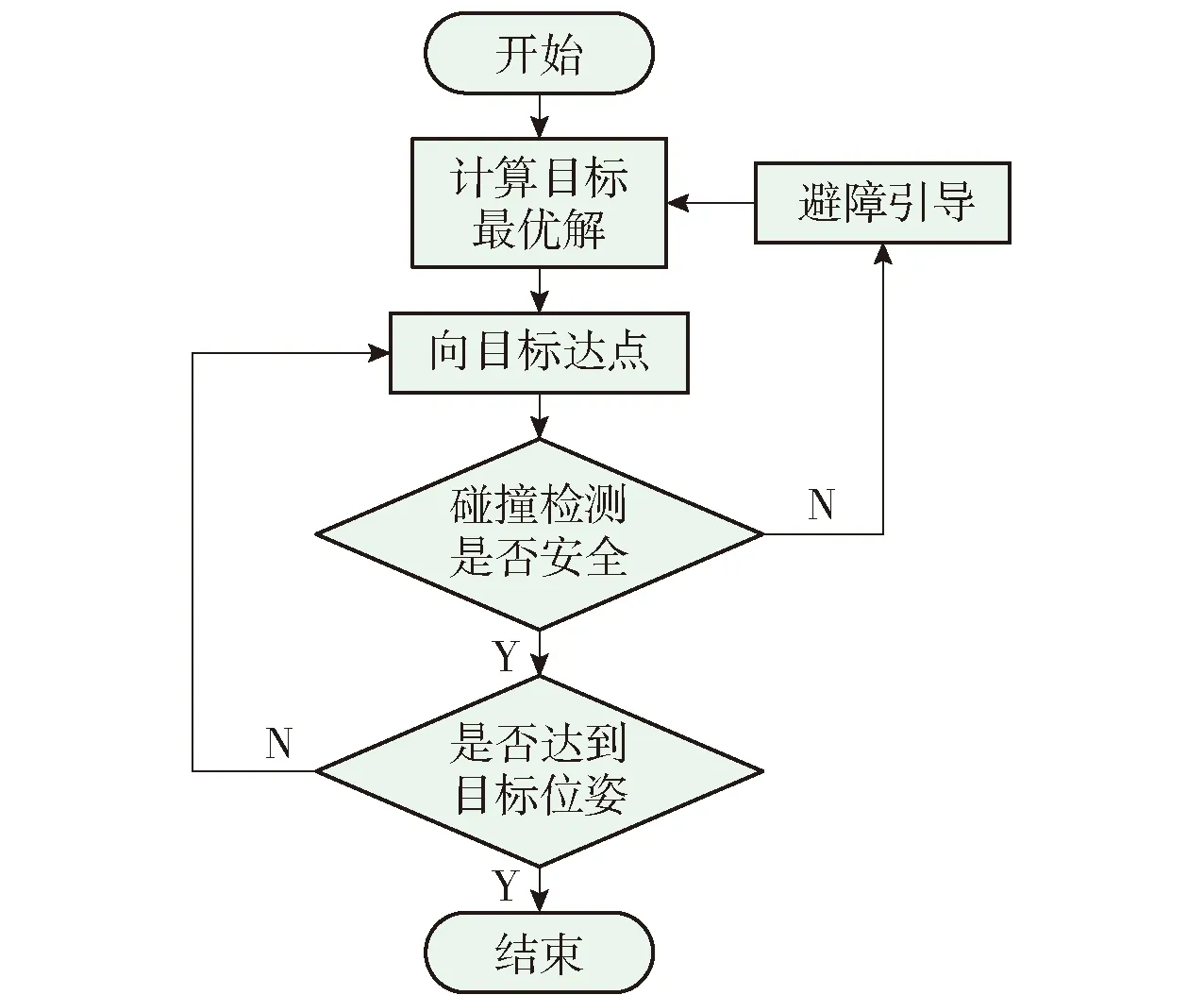
图11 算法流程Fig.11 Algorithm flowchart
3 避障仿真
为验证本文所提出的避障方法的有效性,本文以KUKA iiwa 14 R820机械臂模型对算法进行了仿真,机械臂的具体尺寸参数如表1所示.
仿真实验采用CoppeliaSim4.0(CS)与Matlab(M)的跨平台联合仿真,算法单次迭代时由CS提供实时的目标点、障碍物位置以及机械臂关节角信息,将其传输给M进行实时计算避障规划,同时将规划结果回传给CS进行仿真验证,为检验算法的有效性,仿真在静态和动态2种障碍物环境下分别进行.
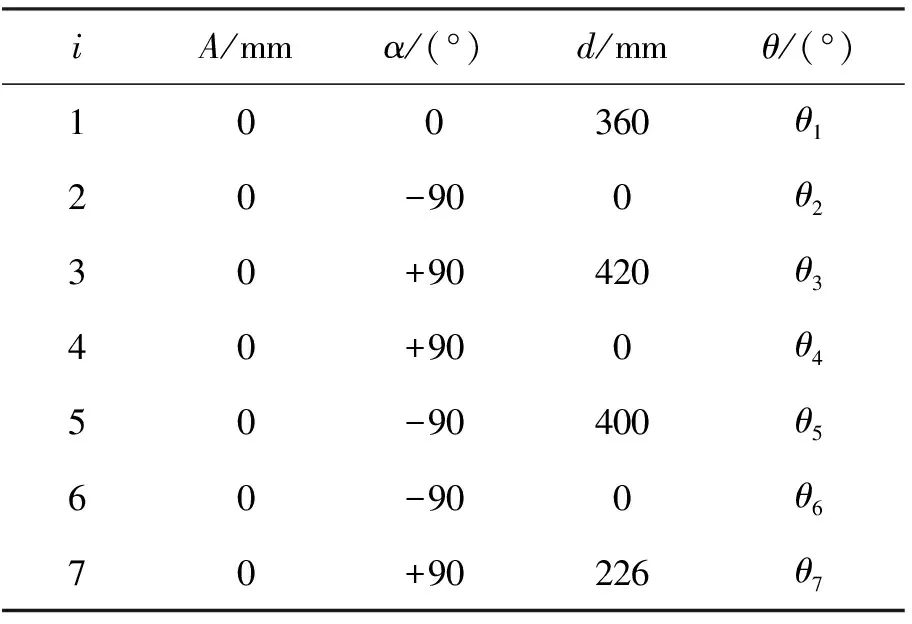
表1 7R机械臂DH参数
3.1 静态障碍物的避障
设定机械臂初始为零位形,待达点的末端目标位置和姿态欧拉角为
Pt,1=[-160 mm,850 mm,750 mm]TPt,2=[-115°,-10°,80°]T
连杆和障碍物的参数
dsafe=100 mm,robs=rL=50 mmPobs=[350 mm,400 mm,900 mm]T
避障算法相关参数
[kθ,1,kθ,2,kθ,3]=[6.5,-10/π,2]T[kd,1,kd,2,kd,3]=[30,3,100]T[kjoi,kre]=[150,10]T
仿真避障过程如图12所示,可以看出机械臂末端在运动到目标位姿的过程中,连杆有效地避开了障碍物. 末端的运动轨迹如图12(f)所示,图中绿色小球为目标点,红色小球为初始点,黑色小球及表面蓝色网格为障碍物以及触发避障规划的安全边界.
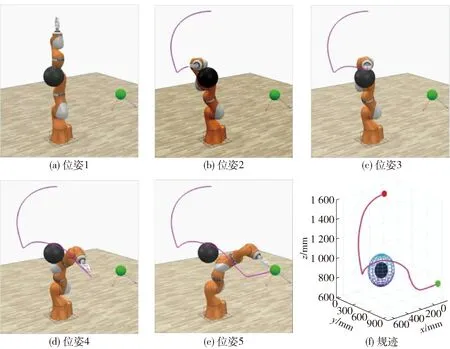
图12 机械臂静态避障的仿真过程Fig.12 Simulation process of static obstacle avoidance
仿真的数值结果如图13所示,从初始零位形开始达点运动,在1.21 s时刻检测到接近障碍物,开始避障引导规划,如图12(b)所示;在2.77 s时刻,完全避开障碍物,继续向目标达点运动,如图12(d)所示. 机械臂的连杆L1为基座-E杆,由于此连杆固连于基座,关节的转动对于杆障关系没有影响,故忽略对于此连杆的距离检测. 从图13(a)可看出在机械臂的运动过程中,各连杆始终与障碍物保持在安全距离之外,结果表明了本文算法在静态障碍物环境中的有效性.

图13 静态避障仿真结果Fig.13 Results of static obstacle avoidance simulation
3.2 正弦动态障碍物的避障
保持其他参数条件不变,将障碍物由静态改为动态正弦运动,设定初始位置和运动速度为
Pobs=[500 mm,400 mm,700 mm]Tvobs=[150 mm/s,100 mm/s,150sin (5t) mm/s]T
障碍物将以正弦波的形式在机械臂达点轨迹上运动,随机性地多次靠近又远离机械臂,如图14所示为在动态障碍物下的仿真过程.
在每次障碍物靠近机械臂时,本文算法都有效地使机械臂避开了障碍物,同时在避障完成后机械臂末端顺利地抵达了目标位姿,完成达点任务.
仿真的数值结果如图15所示,从初始零位形开始运动,在1.44 s时刻首次检测到接近障碍物,开始避障引导规划,在2.11 s时刻,障碍物远离,机械臂继续向目标达点运动,在2.64、3.97、5.22 s时刻,多次与障碍物靠近并在之后及时远离, 每时刻机械臂连杆与障碍物都未发生碰撞,且始终与障碍物保持安全距离,最终实现了达点并避障的任务.

图14 机械臂动态避障的仿真过程Fig.14 Simulation process of dynamic obstacle avoidance
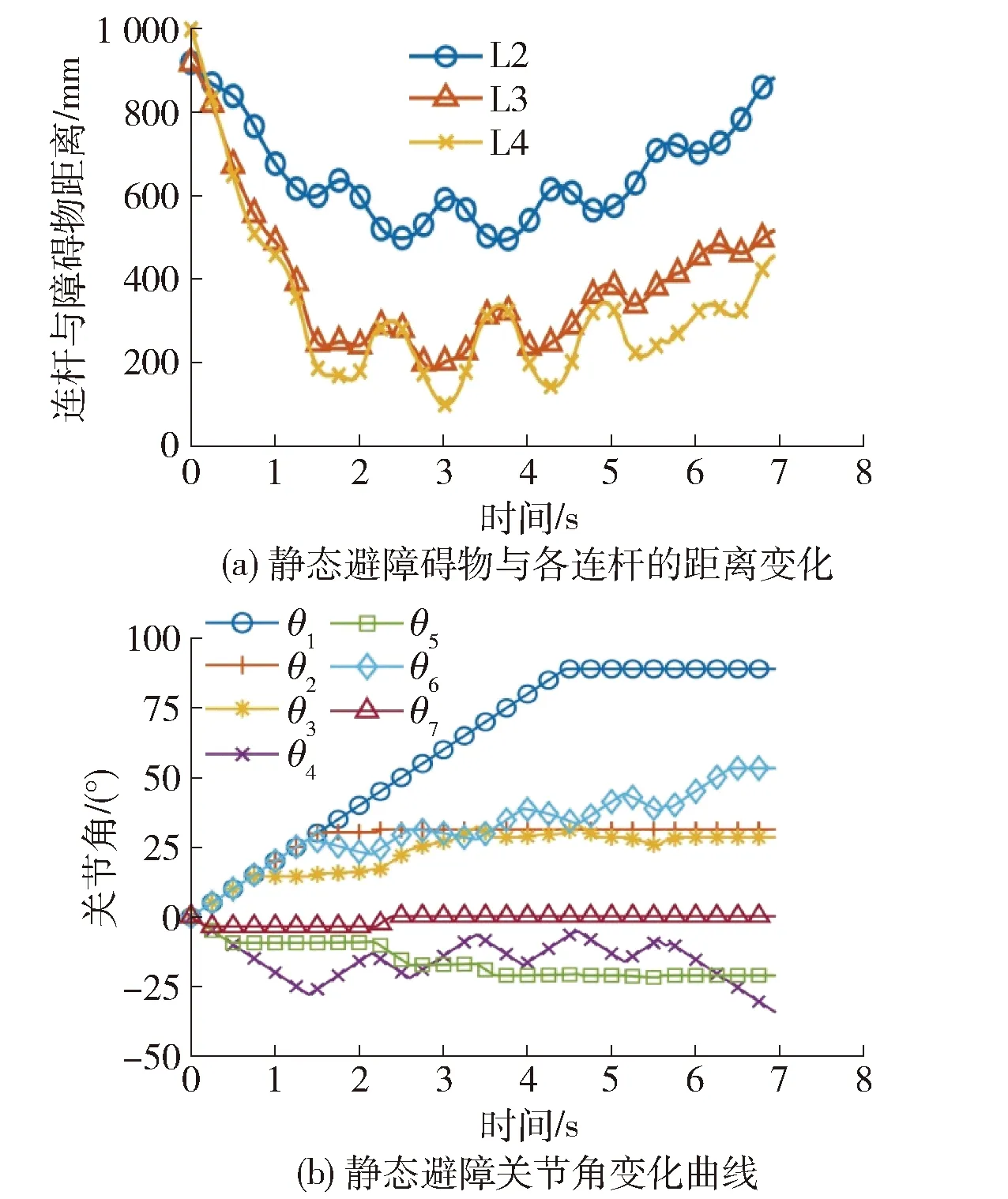
图15 动态避障仿真结果Fig.15 Simulation results of dynamic obstacle avoidance
根据式(2)~(4)计算,在整个运动过程中杆障最小距离为82.27 mm,较好地满足了机械臂在达点运动过程中的避障要求,能及时高效地对机械臂进行实时避障规划,提高在动态环境中的交互安全性. 为进一步验证本文算法的高效性,将本文所提出的实时避障方法与传统人工势场法,在相同的仿真环境和参数条件下进行计算性能对比,实验操作系统为Win10平台,硬件主要参数为CPU:AMD Ryzen1600 3.2 GHz, GPU:GTX1060, RAM:32G,实验结果求取多次计算平均值,如表2所示.
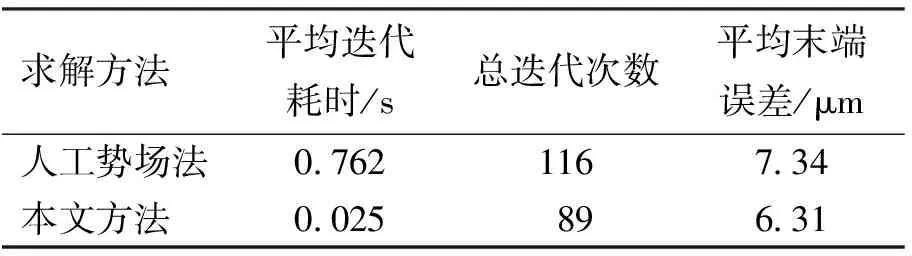
表2 算法性能比较
从表2中可看出,本文避障规划方法的平均单步迭代时间远远小于传统算法,主要由于本文算法将整体的避障规划转化为仅对2根主次危险杆的引导规划,避免了传统算法随着机械臂自由度增多而计算量成倍增加的问题. 因此本文方法能够有效地在动态障碍物环境下实现快速避障的任务.
4 结论
1) 根据杆障的位置关系,确定主次危险杆件,同时对2根连杆进行避障规划,并引入改进的Sigmod函数平滑危险杆件切换时的抖动问题,具有明确的解析形式.
2) 在求解出自运动解集的基础上,构建了关节行程的引力势场和杆障安全距离的斥力势场,在避障完成后从解集中再次选择最优位形解,进行达点运动,避免了陷入局部最小解振荡的问题.
3) 通过仿真证明了本文方法的有效性和实时性,能较好地实现了机械臂在动态障碍物环境下的避障问题,后续将基于本文算法,研究在有关节约束及多障碍物下的避障问题.

