超声波在混凝土中的能量损耗规律

卢青

华南理工大学 广州510640

引言

混凝土是世界上用量最大的建筑材料之一，其在现代化建设中发挥着不可或缺的作用［1］。超声波法［2］是混凝土检测中较为常用的方法，能够快速、无损伤地检测混凝土状况。但混凝土是由水泥、细骨料、粗骨料以及水等物质复合硬化而形成的非均匀多相材料，骨料以及孔隙分布的不均匀性必然会影响混凝土超声波的传播，导致超声波接收信号波形复杂、信噪比低以及能量严重衰减［3，4］。要提高超声波无损检测在混凝土中的应用，首先得了解和认识超声波在混凝土中的传播和能量损失规律。虽然国内外许多学者都认识到超声波在混凝土中传播时骨料、孔隙会造成超声波能量严重衰减，但很少定量计算超声波能量随传播距离的衰减以及骨料、孔隙对超声波能量衰减的影响。Aziz等［5］将混凝土中的骨料分别设置为椭球体和立方体，模拟了20kHz ～150kHz频率范围内超声波在混凝土中的传播，结果表明骨料形状对超声波衰减影响轻微。密士文等［6］研究不同骨料体积分数对超声波能量衰减的影响，认为骨料含量的变化对超声波能量衰减的影响不大。Aboqudais等［7］浇筑不同骨料粒径（最大粒径分别为9.5mm、19.34mm、25mm 和37.5mm）的混凝土，得出骨料粒径越大超声波传播速度越高的结论。Nakahata 等［8，9］研究了超声波能量衰减与频率的对应关系，并且认为骨料的散射是超声波能量衰减的主要因素。目前研究混凝土骨料、孔隙对超声波传播的损耗规律较少，因此，本文根据富勒［10］级配曲线和瓦拉文［11］平面转换公式，用MATLAB编程实现椭圆形骨料的生成和投放，最后将生成的二维数值混凝土模型导入到有限元软件COMSOL Multiphysics 5.6 中进行数值模拟，计算超声波能量随传播距离的衰减以及骨料、孔隙对超声波能量损耗规律的影响，为超声波无损检测提供一定的参考。

1 混凝土中超声波传播的模拟

虽然研究超声波在混凝土中的传播和能量损耗规律可以通过模型试验总结归纳，但需要考虑的影响因素较多且受试验条件以及实验方法的限制，部分试验很难或根本无法进行［12］。而数值模拟可以真实且重复地计算超声波在混凝土中的传播过程，分析不同因素对超声波振幅、频率、波形和能量等参数的影响，不仅大大节省了人力和物力，而且各种因素更加可控。严格来说，混凝土骨料的形状一般是不规则的多面体，而工程实践中也常用卵石作为混凝土骨料，卵石骨料形状与椭圆较为接近且已有学者研究发现骨料形状对超声波能量衰减影响轻微［5］，故本文采用的模型都是基于椭圆形骨料。

1.1 弹性介质中的超声波

相关研究表明［3］超声波在固体中是以应力波进行传播的，并且在内部又会发生反射、折射以及波形转换等现象。本文基于弹性介质模型，利用弹性介质声波方程并结合低反射完美匹配层（PML）［13］吸收边界来模拟超声波在混凝土中的传播过程。

假设不存在体力时，弹性介质的波动方程可分解为纵波和横波，其波动方程为：

式中：φ、ψ分别为介质的纵波和横波的矢量位移势函数；∇2为Laplace 算符；cp和cs分别为纵波和横波波速。

1.2 数值混凝土模型生成方法

混凝土骨料在混凝土中起骨架和支撑作用，是其重要组成部分。因此，数值混凝土模型中骨料的生成和投放是整个过程中的重点。目前最理想的级配曲线是富勒［10］提出的最大密实度曲线，采用该曲线可以使混凝土达到最优的密实度与强度。而后，瓦拉文［11］根据体视学原理将密实度曲线推导成为二维截面内任意骨料粒径D ＜D0出现的概率Pc（D ＜D0），其表达式为：

式中：D0为筛孔直径；Dmax为骨料最大粒径；Pk为骨料体积占混凝土总体积的百分比。

整个生成和投放步骤如下：（1）根据骨料体积分数、混凝土区域面积、骨料最大最小粒径以及级配按照上述公式计算出各级配骨料面积；（2）用蒙特卡罗方法［14］随机生成椭圆长轴、短轴、形心坐标等参数，同时要满足边界条件；（3）判断新产生的骨料是否与已产生的骨料干涉［15］，若产生干涉则重新回到第二步；（4）输出骨料参数。按照上述步骤生成满足级配条件且骨料不发生干涉的数值混凝土模型，将生成的数值混凝土模型保存为mph 文件导入COMSOL 中进行模拟。

2 超声波的损耗规律

超声波在混凝土中传播时会发生复杂的反射、散射和波形转换，造成波形畸变，同时也造成能量损耗，特别是高频成分的能量衰减较大。混凝土内骨料含量、粒径、强度等级以及孔隙等都是影响超声波波形及衰减程度的因素，本文主要研究混凝土骨料含量、骨料粒径以及孔隙对超声波能量衰减的影响，以便为实际检测中合理设置发射探头频率和能量等提供理论支持。

2.1 模型验证

按照1.2节所述方法生成二维数值混凝土模型，模型宽度W ＝600mm，高度H ＝600mm，骨料体积分数Pk＝0.3，骨料最大粒径Dmax＝16mm、最小粒径Dmin＝2mm，骨料设为三级配，各粒级范围为2mm ～7mm、7mm ～12mm、12mm ～16mm。为了验证模拟结果，将模拟结果与混凝土试块（试块宽度和高度与数值混凝土模型一致，长度为250mm）进行对比分析。模拟时发射、接收探头布置在模型上下表面的中点，其中激励信号采用频率为100kHz 的正弦脉冲波。表1 为模拟时所用的材料参数，图1 为发射探头、接收探头实测数据和模拟数据波形对比，为了便于对比将幅值进行归一化处理。

表1 数值模拟所用材料参数［16］Tab.1 Material parameters used in numerical simulation

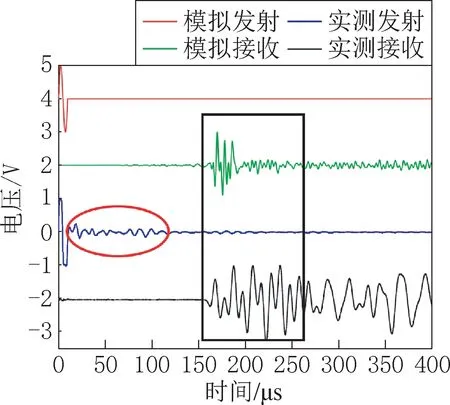
图1 实测和模拟波形Fig.1 Measured and simulated waveforms

从图1 中可知，模拟数据和实测数据趋势大体一致，超声波还未传递到模型下表面时接收信号基本上无波动；接收到信号的起始时间有一定差异，这是由于模拟时材料参数与实际试块有一定误差，即表现为超声波波速差异，从而导致起始时间存在差异；实测数据接收信号持续时间大约为模拟的3 倍（图1 中黑框处），这是由于实测发射信号不可能做到像模拟那样立即停止（图1中红圈处），会有一定程度的滞后，这与发射探头的性能有关。从上述实测波形与模拟波形对比可以验证该模拟方法的正确性。

2.2 孔隙对超声波能量衰减的影响

为研究混凝土中微小孔隙对超声波能量衰减的影响，建立一组有孔隙和无孔隙的数值混凝土模型。无孔隙数值混凝土模型，模型宽度W ＝600mm，高度H ＝400mm，其余参数设置与2.1节相同；有孔隙数值混凝土模型是在无孔隙数值混凝土模型的基础上增加直径1mm、占整个模型比例0.5%的孔隙。为了突出骨料与孔隙的影响同时模拟均匀介质模型，材料参数设置同上。

模拟时发射、接收探头布置在模型上下表面的中点，其中激励信号采用频率为100kHz 的汉宁窗调制正弦脉冲波，模型两侧设置低反射边界。图2 为模拟过程中位移云图，图3 为模型中点处时间-位移曲线，图4 为接收探头接收信号波形及频谱。

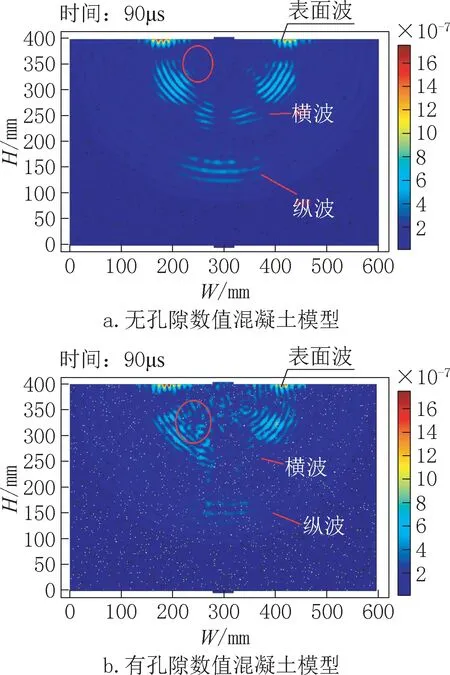
图2 数值混凝土模型位移云图（单位： mm）Fig.2 Displacement nephogram of numerical concrete model（unit：mm）

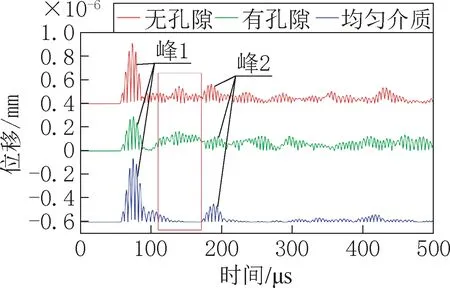
图3 时间-位移曲线（模型中点）Fig.3 Time-displacement curve

图4 接收信号Fig.4 Received signal

从图2 可知，超声波在混凝土中传播时符合弹性波传播理论，表面波波速略小于横波波速，纵波波速最快，但超声波经过骨料和孔隙处时会产生残余振动，且孔隙造成的残余振动明显比骨料更为杂乱，这是因为骨料和砂浆之间的阻抗差小于孔隙和砂浆之间的阻抗差。从图3 可知，超声波第一次和第二次经过模型中点的时间、位移趋势基本一致，但两个峰值之间应是超声波在骨料、孔隙这些界面处来回反射引起（图3 中红框处），降低信噪比；从位移的峰值看出孔隙对超声波能量的影响大于骨料对超声波能量的影响。

从图4a 可知，超声波第一次和第二次经过模型底面反弹后被接收探头接收到的时间、电压趋势基本一致（图4a 中黑框处），但两次有效信号之间应是超声波在骨料、孔隙这些界面处来回反射引起（图4a 中红框处）。将接收到的离散电信号的电压值平方和当作接收信号的能量，则均匀介质、无孔隙和有孔隙混凝土模型的能量值分别为2.667、1.525、0.973，若以均匀介质能量作为基准，则骨料引起有效信号32.6%的能量衰减，孔隙引起有效信号67.4%的能量衰减，孔隙引起的能量衰减占主导地位，这是由于空气与混凝土物质的声阻抗差异非常大，较小的孔隙就能引起较强烈的散射现象，造成有效信号极大地衰减。从图4b 可知，接收信号的回波主要集中在100kHz附近，骨料和孔隙会对高于100kHz 的信号产生较为明显的衰减，对低于100kHz 的信号几乎没影响。

2.3 不同频率超声波在混凝土中的能量损失

建立数值混凝土模型，其中模型宽度W ＝600mm，高度H从50mm 开始按步长50mm 依次增加到600mm，发射信号频率分别采用100kHz、150kHz、200kHz 进行模拟，超声波能量随传播距离变化曲线见图5。

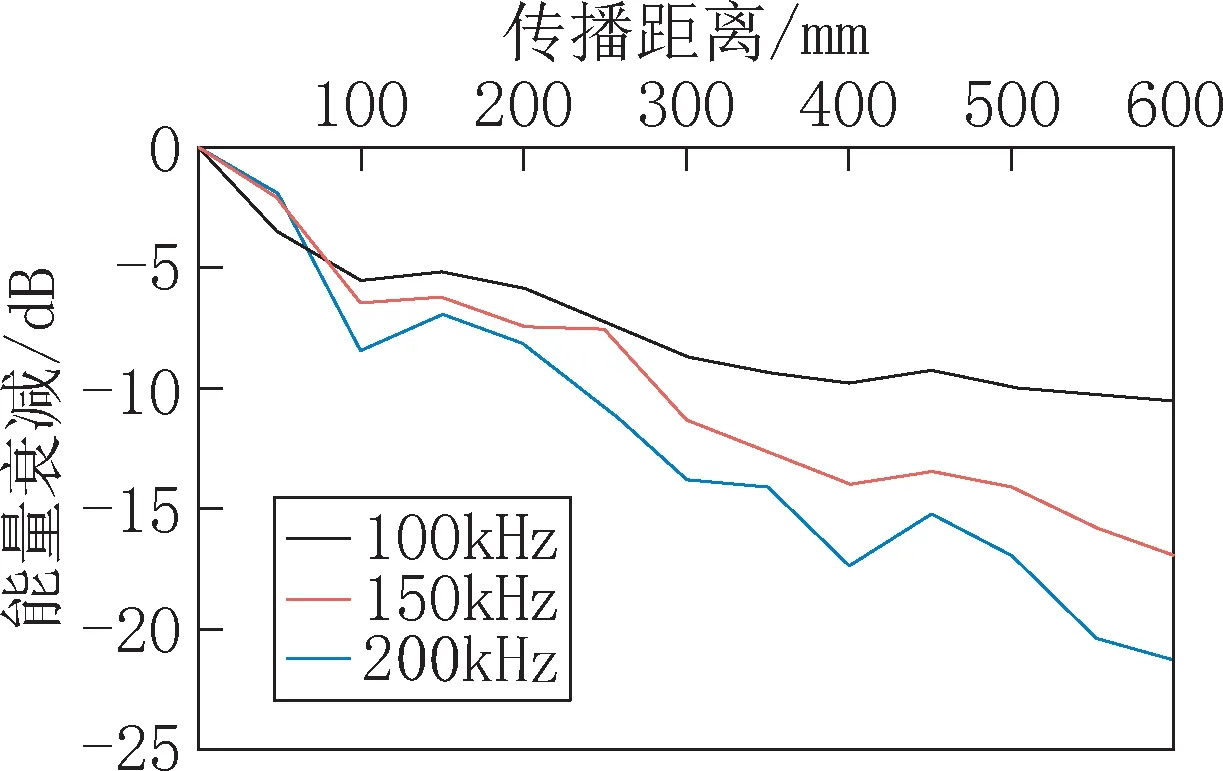
图5 不同频率下超声波能量衰减曲线Fig.5 Ultrasonic energy attenuation curve at different frequencies

从图5 可知，超声波接收信号的能量随传播距离的增大呈指数衰减；传播距离较短时发射信号频率对能量的衰减影响不大，距离更大时发射信号频率越高衰减越快；发射信号频率为200kHz时超声波能量衰减明显快于100kHz，因为频率越高时超声波波长越短，超声波在骨料表面绕射的能力越弱，因此，超声波能量衰减也更大。在实际检测工作中，100kHz 的超声波在分辨率和传播深度方面基本满足要求。

2.4 骨料含量对超声波能量的影响

为研究混凝土中骨料含量对超声波传播的影响，分别对体积分数Pk为0.3、0.5、0.7 的数值混凝土模型进行模拟，除频率采用100kHz 以外，其余设置同前。超声波能量随传播距离的变化曲线如图6 所示。

由图6 可知，在传播距离相同时骨料体积分数越大超声波能量衰减越大，但这种差异非常微小。这是因为骨料数量越多，虽然对超声波的反射、散射越大造成能量衰减越大，但超声波在骨料中的传播速度比在砂浆中传播速度要快，而超声波在高速介质中的衰减程度比低速介质的衰减程度低。综合以上2 个因素得出骨料的体积分数对超声波的能量损耗影响不大。

图6 不同体积分数下超声波能量衰减曲线Fig.6 Ultrasonic energy attenuation curve under different volume fraction

图7 所示为深度400mm 处接收到的超声波形以及频谱对比结果，波形图为了便于对比取接收到信号中波形变化那一段。由图7 可见，骨料体积分数越大，超声波到达的时间越早且引起超声波波形的畸变更复杂，这是因为骨料含量越高混凝土整体波速越大，同时较多骨料也会引起更多反射和散射。

图7 不同骨料体积分数时接收信号Fig.7 Received signal at different aggregate volume fraction

从以上模拟结果可知：混凝土骨料含量对超声波能量损耗差异不明显，说明骨料并不是造成超声波能量损耗的主要因素，但超声波波形随骨料含量的增大变得更加复杂，这会对混凝土内部缺陷的识别造成干扰。

3 结论

1.混凝土是多相非均匀材料，超声波在混凝土中传播时能量随着传播距离呈指数衰减，且发射频率越高能量衰减越快。因此，在利用超声波进行混凝土无损探测时，在满足分辨率前提下应选择主频低的超声发射换能器。

2.超声波的衰减主要由混凝土孔隙引起，受骨料含量的影响较小。虽然不同混凝土中骨料含量、粒径会存在一定的差别，但它们对混凝土中超声波能量及频率的影响趋势是一致的，只是具体数值存在一定差别。

3.利用超声回波法（反射波）进行混凝土无损检测时，发射频率的选择应根据探测深度和骨料大小进行综合选择。超声波频率越高，随探测深度衰减越快，但波长越短、绕射能力越弱有利于提高探测精度。

4.超声波会在骨料之间来回反射，不仅会造成能量损失，还会引起波形发生畸变，增大孔洞等缺陷的识别难度。