大跨度人行桥人致振动研究及控制

宋磊 王虎军 贺小卫

西安市政设计研究院有限公司 710068

引言

城市化建设的加快进行，对市政道路通行能力提出了更高的要求，为保证车行通畅及行人安全过街，交通趋于立体化和分离化，人行天桥得到快速发展［1］。随着人居环境质量的提升，人行天桥不但承担过街通道的作用，而且需融入当地景观，更加注重对美观的追求，大跨、轻柔、纤细成为现代人行天桥的主要特点。弱刚度及低阻尼使得人行天桥的自振频率显著降低，人行荷载作用下结构会出现明显振动，引起行人不适，甚至难以忍受。

例如，英国伦敦千禧桥在开放当日发生大幅横向振动，其中中跨振幅达70mm，南跨振幅达50mm，桥上行人行走困难，甚至依靠栏杆才能保持平衡。事后现场调查和实验室研究表明，人行走时，重心在左右脚之间交替变化，引起横向振动激励，步频约为1Hz，而千禧桥中跨一阶侧向频率低于0.5Hz，二阶频率低于1Hz，南跨一阶侧向频率约为0.8Hz，正好处于行人步频范围之内［2］，同时人群密度较大时，大量行人会自动调整步伐以适应桥梁振动，产生“锁定”现象，又进一步加剧振动。

我国现行《城市人行天桥与人行地道技术规程》（CJJ69—95）仅要求上部结构竖向自振频率不应小于3Hz，而对横桥向动力特性及舒适度评价未做要求，如何合理计算人行天桥动力响应，对其进行舒适度评价，以及预先做好减振设计成为亟待解决的问题。

本文结合国内外相关规范，以一钢管拱式人行天桥为例，建立了人行天桥舒适度评价的人行荷载模型及评价指标，并基于电涡流TMD 进行了减振设计，为同类天桥设计提供参考。

1 人致振动理论

1.1 人行荷载模型

基于人行荷载稳定周期性的特点，单人荷载作用下的竖向及侧向力模型可采用傅立叶级数的形式表达为［3］：

式中：mg 为行人自重，一般采用700N；αv，i、αl，i为竖向及侧向力第i 阶动载因子；fp为步频；φv，i、φl，i为竖向及侧向力第i阶谐波相位角。

SUN＆YAN［4］等人研究成果表明，各阶动载因子受试验条件、试验仪器影响较大，结合英国BS5400规范［5］，单人竖向及侧向人行荷载可表示为：

由于人行荷载具有窄带随机过程的特点，其步长及步频均在一个很窄的范围内随机分布［2］，当桥上行人较多，如人群密度大于1.5人／m2时，部分行人步频接近，当该部分步行力频率与结构的固有频率一致时，激起桥梁振动，从而又进一步导致越来越多的人调整步伐与振动同步，产生更大的激励。ISO 10137 引入同步系数C（n）考虑人群荷载作用，表达式为：

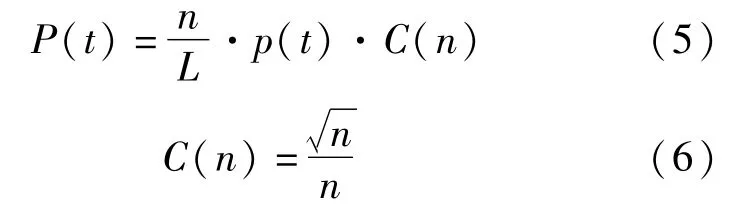
式中：n为桥面行人数；L 为桥长；p（t）为单人荷载；C（n）为同步系数。

1.2 舒适度指标

舒适度指标属于桥梁正常使用状态的评估，目前主要有两种设计思路：避开敏感频率法和限制动力响应值法。避开敏感频率法指结构自振频率偏离步行力步频范围，正常人步行力竖向步频约为1.6Hz ～2.4Hz，侧向步频约为竖向步频的二分之一，即0.8Hz ～1.2Hz［4］，对于大跨、轻柔的现代人行天桥，很难避开此敏感频率范围，而通过增大结构刚度提高频率既不经济又影响景观效果，因此对于此类天桥，该方法不太适用。限制动力响应值法指通过人行荷载作用下结构动力响应分析，限值结构加速度不超过某一容许值，参照德国及法国等人行桥规范［6］，将舒适度定义为：好、中等、差、不可接受四个等级，其分别对应的加速度限值如表1 所示。

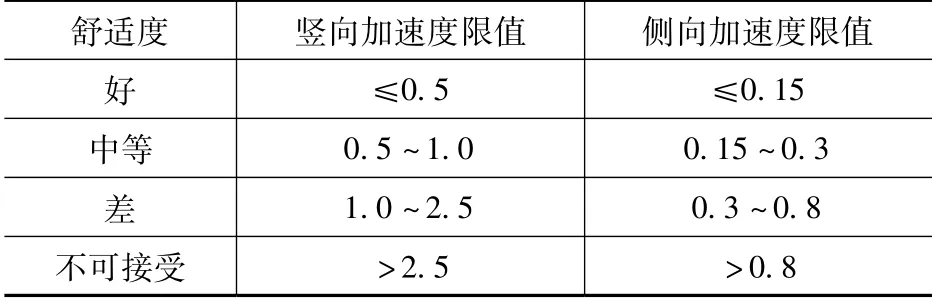
表1 人行天桥加速度限值（单位：m／s2）Tab.1 Acceleration limit index of pedestrian bridge（unit：m／s2）

1.3 人致振动控制

当天桥振动加速度不满足舒适度指标限值时，需进行减振预案设计。TMD（调谐质量阻尼器）为一种广泛采用的被动阻尼减振控制系统，主要由质量块、阻尼器、弹簧构件三部分组成，结构振动时，TMD以不同的相位参与振动，通过增加阻尼，减小动力响应。安装TMD装置后，单自由度结构体系在作用力p（t）下的动力学方程为：

TMD设计时，需考虑三个主要参数：TMD装置与天桥结构的质量比μ、频率比fopt和阻尼比ξopt。考虑舒适度评价采用加速度指标控制，TMD最优频率比和阻尼比采用下式求解［7］：

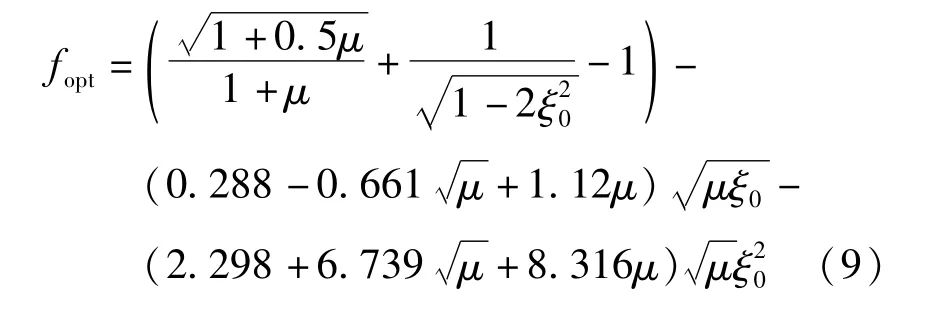
式中：ξ0为天桥主结构阻尼比。

2 工程实例

2.1 工程概况

某钢管桁架无铰拱人行桥，净跨径84m，标准段桥面宽4m，桥两侧各设置2m 宽观景平台，桥面总宽6m。拱肋采用空间钢桁架结构，断面为三角形，主结构桁架宽4.5m。主拱圈直径为1.2m，副拱圈直径为0.5m，联杆为直径0.2m钢管，横向间距2m。拱圈拱轴线为抛物线，方程为：y ＝5／（40 ×40）x2（-42≤x≤42）。该人行桥立面、平面及断面布置如图1 所示。

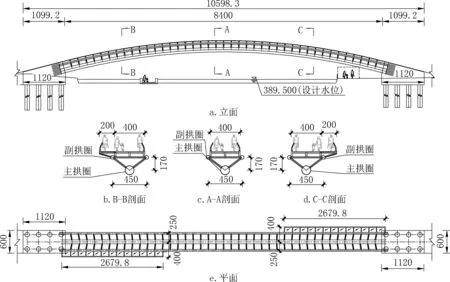
图1 实桥立面、 平面及断面布置（单位： cm）Fig.1 Elevation，plane and section layout of real bridge（unit：cm）

2.2 振动分析及舒适度评价

采用midas. civil建立全桥有限元模型，对其进行模态分析，计算结果如表2 所示。

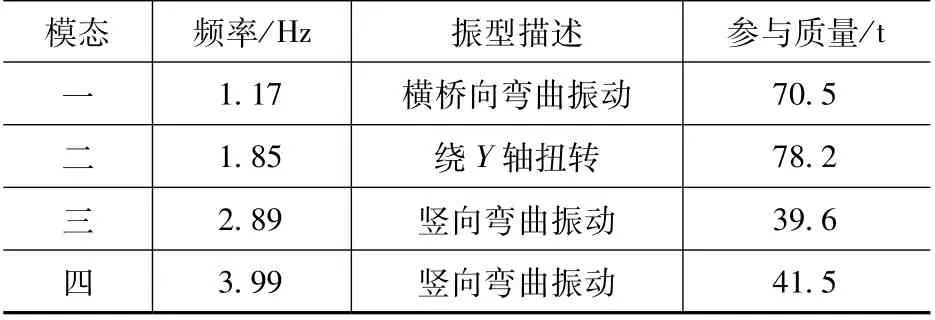
表2 前4 阶自振频率及振型Tab.2 Four natural frequencies and vibration modes of engineering examples

由表2 可见，一阶横向弯曲振动频率为1.17Hz，处于步行力侧向步频0.8Hz ～1.2Hz 范围内；二阶绕Y 轴扭转振动频率为1.85Hz，处于步行力竖向步频1.6Hz ～2.4Hz 范围内；三阶及四阶竖向弯曲振动频率超出步行力竖向步频范围，但第三阶频率不满足我国《城市人行天桥与人行地道技术规范》（CJJ 69—95）关于天桥上部结构竖向自振频率不应小于3Hz 的要求，因此，需对一、二、三阶振动进行动力响应分析，判断其最大加速度是否满足舒适度要求。

建立该人行桥动力响应分析模型，采用时程分析法计算人行荷载作用下上部结构振动加速度，见图2。由图2 可知，一、二、三阶模态最大加速度响应值分别为0.27m／s2、2.01m／s2、2.51m／s2。根据舒适度评价关于加速度指标的限值，各阶模态舒适度评价如表3 所示。由表3 可知，模态一横向振动舒适度评价为中等，可不做处理；模态二及模态三竖向振动舒适度评价分别为差和不可接受，需进行减振设计。

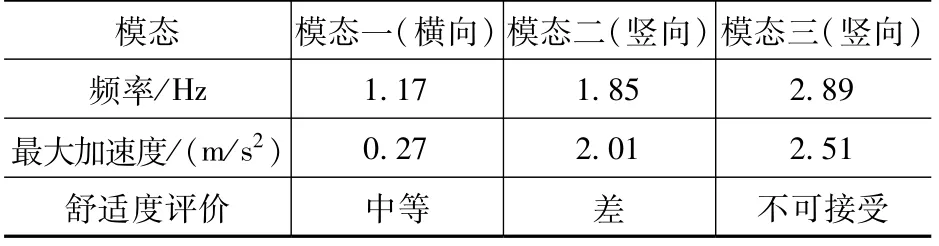
表3 各阶模态舒适度评价Tab.3 Comfort evaluation of each mode

图2 振动加速度响应Fig.2 Vibration acceleration response

2.3 电涡流TMD振动控制

为减小行人不安全感，本工程采用电涡流调谐质量阻尼器进行振动控制。电涡流TMD 克服了传统TMD 易损耗、后期调节难、需要较多维护的特点，同时具有理想的线性粘滞阻尼特性、阻尼系数简单可调、耐久性高。针对该桥动力响应分析结果，建立电涡流TMD 振动控制预案，技术参数见表4。

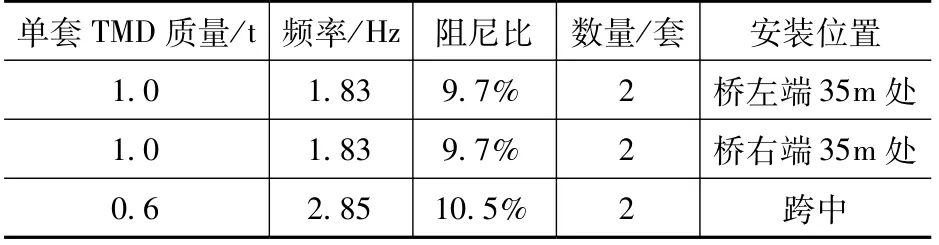
表4 电涡流TMD技术参数Tab.4 Technical parameters of eddy current TMD

在该人行桥动力响应分析模型中考虑TMD技术参数，得到安装TMD 装置后结构加速度响应曲线，如图3 所示。

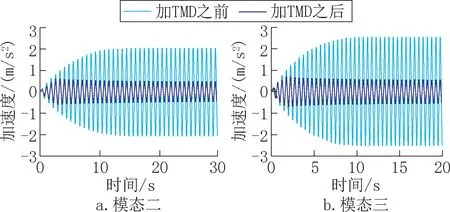
图3 振动加速度响应对比Fig.3 Comparison of vibration acceleration response

由图3 可见，安装电涡流TMD 后，模态二加速度响应由2.01m／s2降至0.49m／s2，舒适度指标为好；模态三加速度响应由2.51m／s2降至0.51m／s2，舒适度指标为中等。

3 结语

本文综合国内外研究成果及相关规范，建立了人行天桥舒适度评价的人行荷载模型及评价指标，基于结构振动理论，通过电涡流调谐质量阻尼器实现结构振动控制，并以一大跨度钢管拱人行桥为例，对其进行动力响应分析及舒适度评价。针对不满足舒适度要求的二、三阶模态，采用电涡流TMD 进行减振控制，取得了很好的减振效果，为同类人行桥设计提供参考。