狭长基槽圆弧滑动抗隆起稳定计算方法探讨

周晨

南京市市政设计研究院有限责任公司 210008

引言

我国行业标准《建筑基坑支护技术规程》（JGJ 120—2012）［1］（以下简称《行标》）、上海市工程建设规范《基坑工程技术标准》（DG／TJ 08-61—2018）［2］（以下简称《沪标》）均规定：锚拉式支挡结构和支撑式支挡结构，当坑底以下为软土时，需要以最下层支点为转动轴心的圆弧滑动模式，验算抗隆起稳定性。此外，国家标准《建筑地基基础设计规范》（GB 50007—2011）［3］也涉及该类抗隆起验算，但计算模型与《行标》和《沪标》略有不同。

以最下层支点为转动轴心的圆弧滑动模式抗隆起验算，假定破坏面为通过桩、墙底的圆弧形，以力矩平衡条件进行分析。一般给水排水管道工程基槽呈狭长型，基槽两侧支挡结构有可能相互限制破坏面的形成，而上述3 个标准都没有针对性规定，如果不进行拓展，其圆弧滑动模式的抗隆起验算规定均不适用于狭长基槽。文献［4］中有限元强度折减法计算结果显示：狭长基槽稳定安全系数随着基坑宽度的减小而增加。有碍于土的本构模型的复杂性等因素，普通工程设计难以完全依赖有限元计算，而在软弱地基区域，圆弧滑动模式抗隆起稳定验算往往控制支挡结构的嵌固深度，因此，有必要针对狭长基槽，对现有的圆弧破坏模式抗隆起计算方法进行拓展，以满足优化管道基槽支护设计的需要。

计算方法的拓展首先要求反映实际破坏情况，同时应与拓展之前有着相同的假定、连续的结果，以及合理的变化趋势。本文从《行标》和《沪标》规定出发，从计算模型一致性及结果合理性角度，讨论圆弧滑动模式抗隆起稳定性验算在狭窄基槽条件下的拓展。讨论时默认支挡结构同时垂直于地面与基槽底面，忽略基槽端部空间效应影响。

1 现行规范基槽抗隆起稳定验算的规定

1.1 行业标准规定

《行标》规定：锚拉式支挡结构和支撑式支挡结构，当坑底以下为软土时，其嵌固深度应符合式（1），以最下层支点为轴心的圆弧滑动稳定性要求。

式中：Kr为以最下层支点为轴心的圆弧滑动稳定安全系数；安全等级为一级、二级、三级的支挡式结构，分别不应小于2.2、1.9、1.7；cj为第j土条在滑弧面处土的黏聚力（kPa）；φj为第j 土条在滑弧面处土的内摩擦角（°）；lj为第j土条的滑弧段长度（m），取lj＝bj／cosθj；qj为第j 土条顶面上的竖向压力标准值（kPa）；bj为第j 土条的宽度（m）；θj为第j 土条滑弧面中点处的法线与垂直面的夹角（°）；ΔGj为第j 土条的自重（kN），按天然重度计算。

《行标》假定圆弧破坏面通过支挡结构底端，以最下层支点为转动轴心，以力矩平衡条件进行分析。图1 中OA 面以上土层只考虑荷载，不计其抗力。计算公式为条分法比值形式，分子部分代表抗隆起力矩，分母部分代表隆起力矩，公式中略去半径，安全系数表现为剪力之比。计算抗隆起力矩时，忽略支挡结构的作用，抗剪强度计算时以竖向荷载垂直于破坏面的法向分力作为正应力。隆起剪力是竖向荷载沿滑动面的切向分力，在基槽内侧为负值。

图1 最下层支点为轴心的圆弧滑动稳定验算Fig.1 Checking calculation of circular arc sliding stability with the lowest fulcrum as the axis center

该方法是我国软土地区习惯采用的方法。实际工程中常常以这种方法作为支挡构件嵌固深度的控制条件［1］。

1.2 上海市地方标准规定

《沪标》与《行标》计算简图相同。计算公式为积分形式［2］，安全系数为力矩之比。

《沪标》隆起力矩与式（1）左侧分母部分乘以破坏面半径R等价。

《沪标》抗隆起力矩计算中，确定抗剪强度时，采用正应力，由竖向荷载垂直于破坏面的分力和竖向荷载引起的水平力垂直于破坏面的分力两部分组成。等价于式（1）左侧分子中“［］”内加上式（2）后，与破坏面半径R的乘积。《沪标》计算竖向荷载侧压力系数时，忽略黏聚力的影响，见式（3）。显然按《沪标》计算所得抗隆起作用比《行标》的更大。

式中：Ka为土的主动土压力系数。

《行标》和《沪标》都没有针对滑动面出土位置受限情况的规定。

2 考虑狭长基槽对抗隆起稳定验算影响的方法

2.1 现有抗隆起计算方法不适用的基槽宽度

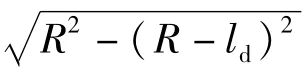
抗隆起计算方法拓展方案的基本要求之一就是安全系数计算结果在基槽宽度等于临界宽度处连续，当基槽宽度小于临界宽度时安全系数将随着基槽宽度变化而变化。

2.2 方法1：以折算荷载考虑狭长基槽影响

如图2 所示，当基槽宽度小于临界宽度时，如果维持《行标》计算简图不变，破坏面ABCD会在图2 中C 点穿过支护结构，同时DE 面以上土荷载qk的作用，会使CD段破坏面隆起与抗隆起力矩同时增加，而由于支挡结构内侧隆起力矩为负值，DE面以上土荷载会降低总隆起力矩，因此，计算中纳入这部分荷载必然会增加安全系数。按《行标》原则不考虑支挡结构本身的作用，再把DE以上土的作用折算成荷载，按原计算模型与公式计算可以认为是一种考虑狭长基槽的拓展方案。

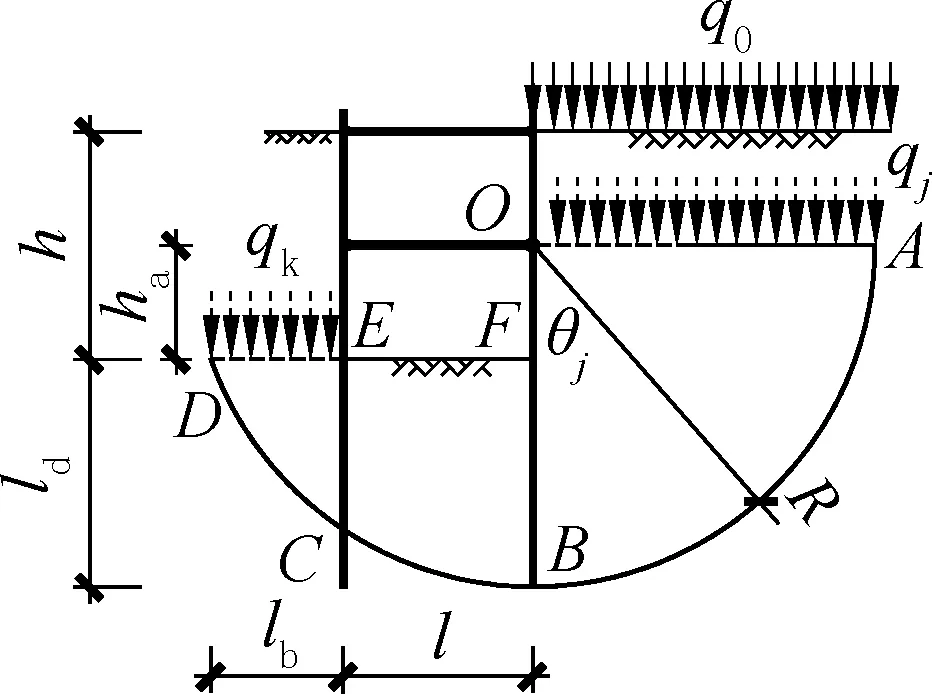
图2 以荷载考虑狭长基槽作用Fig.2 Considering the action of long and narrow foundation pit with load

在维持原有的破坏模式与形态不变的前提下，折算荷载方法足够保守，但实际上不可能发生破坏面穿过基槽另一侧支挡结构的破坏形式。

2.3 方法2：按轴心垂直移动考虑狭长基槽影响

文献［5］基于《沪标》提出了一种破坏面圆弧轴心沿支挡结构垂直向下移动的狭长基槽抗隆起验算方法，见图3。该方案假定：当基槽宽度小于支挡结构嵌入深度时，轴心O位置满足轴心到支挡结构底端的距离等于基槽宽度，此时，破坏面圆弧部分的半径等于基槽宽度。

如图3 所示，该方案破坏面为ABCDE，其中BCD部分为圆弧，其隆起与抗隆起力矩计算与《沪标》一致；AB、DE 两段为直线段，计算时，采用土体竖向荷载产生的侧压力作为正应力，其中AB段破坏面在土中，内摩擦角为φk，DE段破坏面在土体和支挡结构之间，摩擦角δk为（2／3 ～3／4）φj。AB、DE两段抗隆起力矩计算见式（4）、式（5）［5］。

图3 以轴心垂直移动考虑狭长基槽作用Fig.3 Considering the action of long and narrow foundation pit with the vertical movement of axis center

式中：MRLKx为基槽外开挖面以下圆弧破坏面轴心以上抗隆起力矩标准值（kN·m）；MRLKy为基槽内开挖面以下圆弧破坏面轴心以上抗隆起力矩标准值（kN·m）；hb为开挖面至圆弧破坏面轴心距离（m）；h为微分段距离开挖面的距离（m）；γ 为与h对应土层的比重（kN／m3）；φk为与h对应土层的内摩擦角标准值（°）；δk为与h 对应土层与支挡结构之间摩擦角标准值（°）。

从破坏模式角度，轴心垂直移动方法比折算荷载方法更合理，但垂直移动轴心方法破坏面存在直线段，而直线段正压力对轴心产生的力矩不为0，不符合力矩平衡条件。

当基槽宽度介于临界宽度和支挡结构嵌固深度之间时，垂直移动轴心方法基槽内侧的破坏面不存在直线段。

2.4 方法3：按轴心水平移动考虑狭长基槽影响

方案3 如图4 所示，当基槽宽度小于临界宽度时，把圆弧破坏面轴心O水平移动，使其满足如下两个条件：一是O点高程不变，二是破坏面圆弧通过支挡结构的底端和狭长基槽的另一侧支挡结构入土点。

图4 以轴心水平移动考虑狭长基槽作用Fig.4 Considering the action of long and narrow foundation pit with the horizontal movement of axis center

显然轴心水平移动方法可以保证破坏面不穿过支挡结构。同时圆弧破坏面ABCD 发生破坏时，块体OACDF 水平不动点位于最下一道支撑相同高程，最接近《行标》和《沪标》的基本计算简图。该模型中EF 段以上土体作为荷载参与计算，显然考虑该段土体荷载可以提高安全系数计算结果。

水平移动轴心方法O点位置和破坏面的半径R可以根据支挡结构嵌入深度、最下一道支撑位置和基槽宽度等尺寸之间的几何关系确定，见式（6）、式（7）。

式中：la为圆弧破坏面轴心水平偏移（m）；Rl为最下层支点至支挡结构底端距离（m）；ld为支挡结构嵌固深度（m）；l 为基槽宽度（m）；R 为圆弧破坏面半径（m）。

2.5 方法4：按轴心正交移动考虑狭长基槽影响

如果方法3 不考虑圆弧破坏面轴心高程等于最下一道支撑高程这一条件，会存在多个满足要求的轴心，这些轴心位于直线OO′上（见图5）。轴心点不能位于基槽内侧，否则基槽内不完全是隆起区域；轴心也不能位于开挖面以下，否则滑动面会与另一侧支挡结构相交。经试算比较，均匀土层时，当轴心位于直线OO′与支挡结构或槽底的延长线交点时，有最小的安全系数。因此，一般情况，圆弧破坏面轴心分别沿支挡结构和槽底延长线移动可以得到相对最小的安全系数。

方法4 具体做法如图5 所示：当槽宽介于特征宽度和支挡结构嵌固深度之间时，轴心位于支挡结构上，当基槽宽度小于支挡结构嵌固深度时，轴心位于槽底延长线上。该方法计算的结果，基本可以认为是符合破坏面为圆弧和力矩平衡条件所可能破坏面中安全系数最小的结果。轴心具体位置同样可以根据几何关系确定，见式（8）～式（10）。

图5 以轴心正交移动考虑狭长基槽作用Fig.5 Considering the action of long and narrow foundation pit with the orthogonal movement of axis center

式中：la为圆弧破坏面轴心水平偏移，坑外为正，la≥0（m）；hl为圆弧破坏面轴心到开挖面距离，上方为正，hl≥0（m）。

3 试算比较

3.1 试算条件

以一个管道工程常用的基槽支挡结构为例进行试算，参数如下：基槽深6m，支挡结构采用12m长板桩，板桩嵌固深度6m，内设2 道支撑，最下一道支撑距槽底3m。土的天然重度取18kN／m3，均匀土层，黏聚力标准值ck＝10kPa，内摩擦角标准值φk＝15°，地面超载取20kPa。分别按前述4 种方法针对不同基槽宽度进行试算。另外，取基槽深度分别为10m、20m 进行对比。

3.2 试算方法与原则

水平移动轴心、折算荷载和正交移动轴心方法，按《行标》条分法公式计算，截条宽度按槽外部分等分1000 条确定，槽内部分条宽与槽外部分相近。抗剪强度计算不考虑竖向力引起的侧压力作用。

竖向移动轴心方法参考《沪标》采用积分公式计算，其中，土与支挡结构之间摩擦角取2／3φk。与其他方案对比时，参考《行标》不考虑竖向力引起的侧压力作用，仍保留黏聚力作用。竖向移动轴心方法基槽宽度介于临界宽度与支挡结构嵌固深度之间时，轴心位于最下层支撑和槽底之间，此时破坏面假设为槽内外不等长的两段圆弧，这部分与正交移动轴心方法简图相同。

计算时，地面超载对结构有利时，不参与安全系数计算；土自重按实际情况考虑。

3.3 试算结果讨论

由图6a 和表1 可知：基槽深度6m 的算例中，当基槽宽度大于等于临界宽度时，按《行标》计算的抗隆起稳定安全系数为1.43，条分法和积分公式法结果略有差异；按《沪标》计算得到的最小安全系数为1.76。

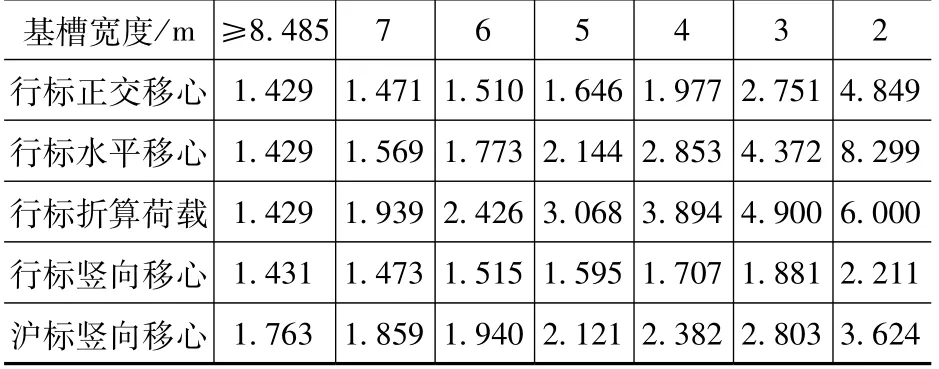
表1 不同基槽宽度安全系数（基槽深度6m）Tab.1 Safety factors of different foundation pit widths in various schemes（Foundation pit depth 6m）

由图6 可知：当基槽宽度小于临界宽度时，各种算法得到的安全系数均随着基槽宽度减小而增加。在基槽宽度略小于临界宽度时，按《行标》折算荷载法计算的安全系数增速度最快。在基槽宽度在临界宽度和支挡结构嵌固深度之间时，按《行标》调整后的竖向移动轴心法和正交移动轴心法计算的安全系数相同且增长最慢。当基槽宽度小于支挡结构嵌固深度时，采用正交移动轴心法安全系数高于竖向移动轴心法。当基槽宽度足够小时，水平移动轴心法计算出的安全系数最高。按《行标》调整后的竖向移动轴心法计算的安全系数始终增长缓慢。

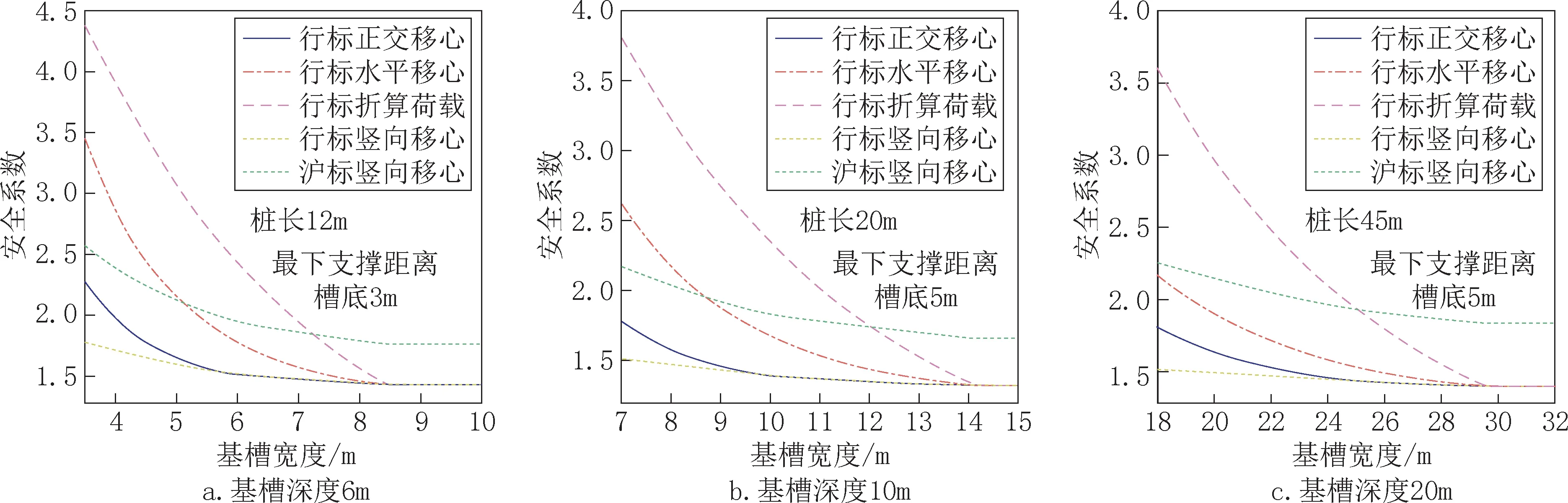
图6 不同计算方法下安全系数与基槽宽度关系Fig.6 Relationship between safety factor and foundation pit width under different calculation methods

按《行标》调整后的竖向移动轴心法计算所得结果最安全，但当基槽宽度较小，显然不可能发生圆弧模式破坏时，安全系数结果仍偏小，缺乏经济性；采用折算荷载法计算时，当基槽宽度略小于临界宽度时安全系数增长过快，不够安全；采用水平移动轴心方法当基槽宽度接近临界宽度时，随着基槽宽度减小，安全系数增长略高于垂直移动轴心法，当基槽宽度进一步减小时，水平移动轴心法的安全系数迅速增加。

正交移动轴心法所得结果，接近于同时满足破坏面为圆弧假定和力矩平衡条件的最小安全系数，在基槽宽度较小时安全系数增长变快，也符合预期。因此，正交移动轴心法可以兼顾安全性和经济性。

4 结语

维持弧形破坏面力矩平衡条件，对狭长基槽抗隆起稳定验算进行拓展，一般用于基槽宽度略小于临界宽度的情况。随着基槽进一步狭窄，基槽两边外侧的滑动力相互影响效应明显，将不会发生圆弧形态的隆起破坏，此时只能采用其他方法，如有限元强度折减法，来分析基槽支挡结构的抗隆起稳定性。

当基槽宽度略小于临界宽度时，采用水平移动圆弧破坏面轴心方法，对狭窄基槽圆弧滑动抗隆起验算进行拓展，是最接近现行规范假设的方法。如果不限制轴心的高度，按正交移动轴心方法有着更高的安全度，是合理且稳妥的推荐方法。

在给水排水管道基槽设计中，针对狭长基槽对圆弧滑动抗隆起稳定计算方法进行拓展是有必要的，今后需要进一步积累数据和验证。