分数阶非线性系统PDα型迭代学习控制收敛性分析
张克军, 彭国华, 杜永军
(1.徐州工程学院 数学与统计学院, 江苏 徐州 221018; 2.西北工业大学 数学与统计学院, 陕西 西安 710129; 3.兰州理工大学 经济管理学院, 甘肃 兰州 730050)
随着分数阶微积分理论和其他智能优化算法的发展,对于复杂度不断提高的控制系统,为了实现对其输出轨迹的精确跟踪,一些学者提出了分数阶迭代学习控制算法.2001年,陈阳泉等[1]首次提出了Dα型分数阶迭代学习控制算法,将迭代学习控制的应用从整数阶系统扩展到了分数阶系统.经过二十年的发展,针对不同类型的分数阶系统,Lazarevi、李岩、兰永红等[2-12]对分数阶迭代学习控制算法的收敛性和鲁棒性等学习性态进行了深入研究,并取得了一系列的成果.
与线性系统相比,分数阶非线性系统在自然界和工程技术领域里更具有普遍性,对其研究也更加复杂,相应的成果也不多.对于分数阶非线性系统,李岩等[13]利用上确界范数讨论了开环P型迭代学习算法的学习性态.针对一类单输入单输出的分数阶非线性系统,兰永红等[14]对高阶开环P型迭代学习算法的收敛性进行了探索性研究.进一步,针对单输入单输出的分数阶非线性时滞系统,兰永红等[15-16]分别分析了一阶、二阶P型迭代学习算法的收敛性问题.类似的研究还有文献[17,18].此外,对于任意初态的分数阶非线性系统,Lan[19]提出了基于初值学习的开环和闭环P 型迭代学习算法,获得了系统跟踪误差收敛的充分条件.
在上述研究分数阶非线性系统的迭代学习算法收敛性的文献中,主要研究了P型迭代学习算法的收敛性,而关于PDα型分数阶迭代学习算法收敛性的研究还很少.李蕾等[20]对一类单输入单输出(SISO)的分数阶非线性连续系统的PDα型分数阶迭代学习算法的收敛性进行了讨论.然而,上述研究只是针对分数阶仿射非线性连续系统的,限制了其应用的范围.
在现有的研究迭代学习控制的文献中,一般采用λ范数进行范数理论分析,然而,这种方法是有缺陷的.比如,当λ取值很大时,虽然可以在理论上保证控制算法是收敛的,但是在系统重复运行时,其瞬时跟踪误差的上确界值超出了工程实际应用的容许范围,由于误差的累积导致整个系统不能正常运行[21-22].与λ范数相比,Lebesgue-p(Lp)范数不仅考虑了函数f在每个运行时刻函数值p次方的积分,而且考虑了函数f在整个运行区间上的上确界值.因此,在量化和反映函数f的性态方面,Lp范数更有优势[23].
受上述问题的启发,对于一类更一般的SISO分数阶非线性连续系统,本文利用卷积的推广Young不等式和Lp范数,对开环、闭环以及开闭环PDα型分数阶迭代学习算法收敛的充分条件进行了讨论,并利用仿真实验验证了理论的正确性和可行性.
1 预备知识
定义1设f:[0,T]→Rn为一连续向量函数(f(t)=[f1(t),f2(t),…,fn(t)]T),其上确界范数与Lp范数分别为

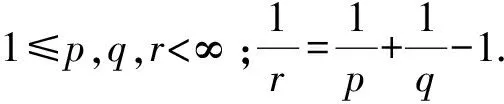
定义2[24]函数f(t)在[t0,t]上的α阶分数阶积分与Caputo型α阶导数分别为
其中:α∈R+;[α]为α的整数部分;Γ(·)为Gamma函数.
引理2[25]设f(x(t),t)是一连续函数,则初值问题
的解等价的Volterra型非线性积分方程为
2 问题描述及分析
针对一类SISO的分数阶仿射非线性连续系统:
(1)
李蕾[20]讨论了PDα型分数阶迭代学习控制算法的收敛性问题.下面,本文考虑一类更一般的SISO分数阶非线性连续系统,具体描述如下:
(2)
其中:t∈[0,T],α∈(0,1);f(·)是结构和参数未知的非线性向量函数;xk(0)∈Rn为系统的初态;xk(t)∈Rn、uk(t)∈R、yk(t)∈R分别为系统的状态向量、控制输入和系统输出;C∈R1×n为常数矩阵.
为了证明方便,给出文中算法的合理假设:
假设1分数阶非线性系统(2)在固定区间[0,T]上重复运行时,系统的初态等于期望初态,即对于∀k∈N+,有xk(0)=xd(0).
假设2分数阶非线性系统(2)的期望输出yd(t)在[0,T]上α阶微分存在;对于给定的yd(t),存在唯一期望控制输入ud(t)和理想状态xd(t),使得
(3)
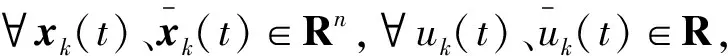
其中:kf为大于零的常数.
假设4函数f关于uk(t)的导数存在,关于xk(t)的每个分量的偏导数都存在,且满足下列条件:
其中:γ1、γ2和M2均为大于零的常数.
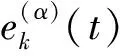
(4)
其中:u1(t)为首次控制输入,可取任意值;ΓP1、ΓD1分别为比例和微分学习增益;ΓP2、ΓD2分别为比例和微分反馈增益.
定理1设分数阶非线性系统(2)满足假设1~4,当开闭环PDα型控制算法(4)被应用于系统(2)时,若满足条件:
2)ρ2ρ1<1,其中:
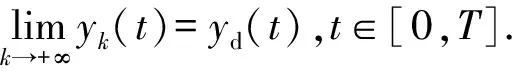
证明设
由系统(2)可知:
ek(t)=yd(t)-yk(t)=CΔxk(t)
(7)
(8)
由式(4),可得
(9)
将式(7,8)代入式(9),得
Δuk+1(t)=Δuk(t)-
ΓP1CΔxk(t)-ΓP2CΔxk+1(t)-
ΓD1(Cfu(xd(t),ξu,k(t),t)Δuk(t)+
Cfx(ζx,k(t),uk(t),t)Δxk(t))-
ΓD2(Cfu(xd(t),ξu,k+1(t),t)Δuk+1(t)+
Cfx(ζx,k+1(t),uk+1(t),t)Δxk+1(t))=
(1-ΓD1Cfu(xd(t),ξu,k(t),t))Δuk(t)-
ΓP1CΔxk(t)-ΓP2CΔxk+1(t)-
ΓD2Cfu(xd(t),ξu,k+1(t),t)Δuk+1(t)-
ΓD1Cfx(ζx,k(t),uk(t),t)Δxk(t)-
ΓD2Cfx(ζx,k+1(t),uk+1(t),t)Δxk+1(t)
(10)
所以
(1+ΓD2Cfu(xd(t),ξu,k+1(t),t))Δuk+1(t)=
(1-ΓD1Cfu(xd(t),ξu,k(t),t))Δuk(t)-
ΓP1CΔxk(t)-ΓP2CΔxk+1(t)-
ΓD1Cfx(ζx,k(t),uk(t),t)Δxk(t)-
ΓD2Cfx(ζx,k+1(t),uk+1(t),t)Δxk+1(t)
(11)
式(11)两边同时取范数,可得
(12)
因此
t|Δuk+1(t)|≤s|Δuk(t)|+
(13)
其中:
式(13)两边同时取Lp范数,可得
(14)
根据引理2和系统(2),可得
(15)
所以
Δxk(t)=
(16)
式(16)两边同时取范数,可得
(17)
进一步,式(17)两边同时取Lp范数,可得
(18)
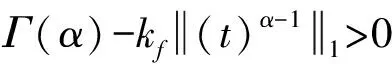
(19)
将式(19)代入式(14),得
(20)
因此
即
(21)
根据条件2),可得
(22)
由式(19,22),可得
(23)
对式(7)两边同时取Lp范数,可得
(24)
进一步,由式(23,24),可得
所以
定理证毕.
当ΓP2=ΓD2=0时,开闭环PDα型算法(4)退化为典型的一阶开环PDα型算法:
(25)
当开环PDα型算法(25)被应用于系统(2)时,有如下结论:
定理2当一阶开环PDα型算法(25)被应用于满足假设1~4的分数阶非线性系统(2)时,若满足条件:
2)0<ρ1<1,其中:
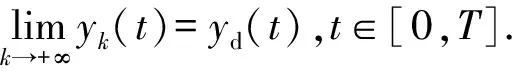
当ΓP1=ΓD1=0时,开闭环PDα型算法(4)退化为一阶闭环PDα型算法:
(26)
当闭环PDα型算法(26)被应用于系统(2)时,获得以下结论:
定理3当一阶闭环PDα型控制算法(26)被应用于满足假设1~4的分数阶非线性系统(2)时,若满足条件:
2)0<ρ2<1,其中:
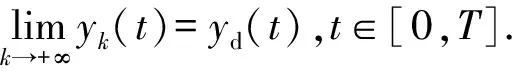
注1与λ范数意义下的收敛条件ρ*=s·t-1<1(s=max{|1-ΓD1γ1|,|1-ΓD1γ2|},t=min{|1+ΓD2γ1|,|1+ΓD2γ2|})相比,对于SISO的分数阶非线性连续系统,在Lp范数意义下,开闭环PDα型控制算法的收敛条件比较保守,但控制算法的收敛性分析和跟踪误差的度量不依赖参数λ的取值,只要满足算法收敛的充分条件,随着迭代次数的增加,就可保证系统输出对期望输出的精确跟踪,无需调整系统运行区间或修改控制算法.
注2由定理1和定理2的收敛条件可知,当ρ2ρ1<ρ1<1时,开闭环PDα型控制算法(4)的收敛速度比一阶开环PDα型控制算法(25)的收敛速度快.
注3定理1的收敛条件ρ2ρ1<1不要求必须满足ρ1<1或ρ2<1.因此,对于控制算法(4)中的增益,这里有更多的选择.
3 仿真实验
为验证理论分析的结果,考虑如下一类SISO的分数阶非线性系统:
(27)
其中,系统的运行区间为[0,1].
由于
因此,kf=0.3,M2=0.3,γ1=γ2=0.42.
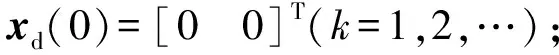
在一阶开环PDα型控制算法(25)中,设置相关参数为:α=0.9,ΓP1=0.2,ΓD1=0.65,计算可得ρ1=0.977 3<1,满足定理2的收敛条件.
当开环PDα型算法(25)被应用于分数阶非线性系统(27)时,图1表示系统第6次、第15次运行时的系统输出曲线,图2为系统跟踪误差曲线在上确界范数和L2范数意义下的变化趋势图.

图1 一阶PDα型算法在第6和第15次迭代的输出
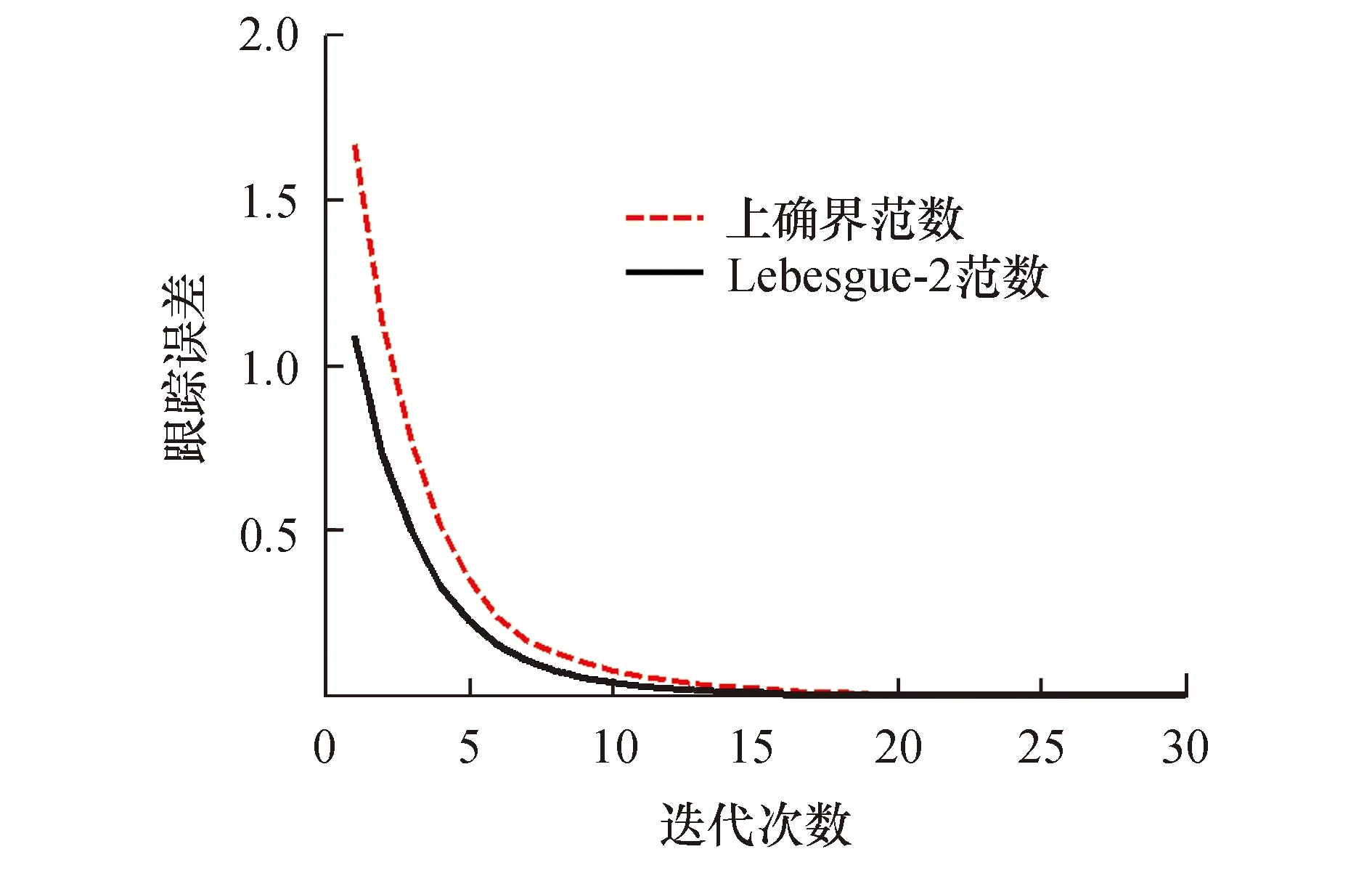
图2 一阶PDα型算法的跟踪误差变化趋势
由图1和图2可知,系统的实际输出随着迭代次数的递增,实现了对期望输出的完全跟踪,且跟踪误差在两种范数意义下均收敛到零.上述结果表明,对于分数阶非线性系统(27),PDα型算法(25)是可行的和有效的.
在开闭环PDα型控制算法(4)中,设置相关参数为:α=0.9,ΓP1=0.2,ΓD1=0.65,ΓP2=0.1,ΓD2=0.8.可以算出ρ1=0.977 3<1,ρ2=0.892 4<1,且ρ2ρ1<ρ1<1,满足定理1和定理2的收敛条件.
在上述条件下,图3给出了一阶开环PDα型控制算法(25)、开闭环PDα型控制算法(4)分别被应用于分数阶非线性系统(27)时,系统的跟踪误差变化曲线.

图3 一阶开环、开闭环PDα型算法的跟踪误差对比
由图3可知,在L2范数意义下,随着迭代次数的递增,上述两种情况下的跟踪误差均是收敛到零的.当ρ2ρ1<ρ1<1时,系统在算法(4)作用下,只需要迭代9次,跟踪误差就能够达到误差范围(0.001),而在传统的一阶开环PDα型算法(25)作用下,系统需要13次迭代,跟踪误差才能达到上述效果.可见,如果选取适当的增益,开闭环PDα型控制算法(4)拥有比开环PDα型控制算法(25)更快的收敛速度.这一结果与注2的结论是相符的.
4 结论
针对一类SISO分数阶非线性系统,本文以PDα型分数阶迭代学习算法为例,利用卷积的推广Young不等式,研究了开环、闭环以及开闭环PDα型算法在Lp范数意义下收敛的充分条件,发现:PDα型算法的收敛条件主要取决于算法的增益以及系统的自身属性,且在选取适当增益的情况下,开闭环PDα型算法拥有比开环算法更快的收敛速度.这些结论与分数阶线性系统的相关结论是一样的.
本文只分析了SISO的分数阶非线性连续系统一阶PDα型控制算法的收敛条件,类似地,可以继续讨论高阶PDα型控制算法的收敛性和鲁棒性问题.

