滚珠丝杠进给系统轴向动态特性参数识别

吴 沁, 谌国章

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

滚珠丝杠进给系统具有传动精度高、寿命长和高性价比等优点，已成为数控机床进给系统的主要传动方式[1].该系统由丝杠、丝杠螺母副、工作台、伺服电机、导轨、联轴器和左、右轴承副等零部件通过不同的结合部组成，其刚度和阻尼参数对机床的加工性能、振动特性和结构优化有重要影响.因此，正确、高效地识别滚珠丝杠进给系统动态特性参数备受关注.

滚珠丝杠进给系统主要有2种类型的结合部，即固定结合部和滚动结合部.目前，识别结合部参数的方法有理论计算法、实验测试法及理论计算和实验测试结合法[2].对于固定结合部参数的识别，赵宏林等[3]从基本动力学方程出发推导出刚度和阻尼理论计算公式，汪振华等[4]通过实验测试获得了固定结合部的动态特性参数，王立华等[5]通过理论计算和实验测试相结合的方法对铣床结合部的特性参数进行识别.对于滚动结合部参数的识别，Dong等[6]通过子结构间耦合关系建立机床结合部动力学模型，运用最小二乘法识别出了等效动刚度，理论结果与实验结果相吻合.陈勇将等[7]通过滚道上所受的力和力矩平衡方程，根据刚度定义得到滚珠丝杠副的刚度矩阵，并对影响滚珠丝杠副刚度的因素进行研究.以上研究所用的理论计算法过程复杂且可靠性低，仅适用于单个滚珠丝杠副、轴承结合部的研究，不适用于进给系统滚动结合部的刚度计算.Zhang等[8]通过混合单元法建立滚珠丝杠进给系统等效动力学模型，在考虑进给速度的影响下，推导出单个部件的等效轴向刚度和系统总传动刚度.Zhu等[9]建立滚珠丝杠进给系统轴向参数识别模型，通过遗传算法优化识别出滚动结合部刚度和阻尼参数，理论计算值与实验测试值误差较小.以上研究所用的实验测试法准确有效，但需要定制的实验台，有时难以满足实验条件.Chen等[10]通过准静态分析方法推导出接触刚度矩阵，进一步描述滚珠丝杠的动态特性.Jiang[11]根据赫兹接触理论，计算了滚珠丝杠副导轨的刚度，并研究了载荷对结合部刚度的影响规律，比有限元法和参数识别法简单、有效.以上研究所用的理论计算和实验测试相结合的方法需要获取结合部的频响函数，但在实际进给系统中不便对轴承、导轨等零部件进行实验测试，故不适用于进给系统滚动结合部参数的识别.

本文针对目前存在的问题，首先，建立简谐激振力作用下丝杠和工作台的轴向振动方程和参数辨识模型;然后，根据激振力幅值、频率、各支撑点间距离和测量处的振幅等参数建立优化目标函数;最后，采用粒子群遗传混合算法识别出刚度和阻尼参数.

1 滚珠丝杠进给系统动力学建模

1.1 滚珠丝杠进给系统结构

滚珠丝杠进给系统是复杂的弹性系统，如图1所示，主要包括伺服电机、联轴器、左轴承副、右轴承副、丝杠螺母副、导轨和工作台.伺服电机通过联轴器和丝杠螺母副将丝杠的旋转运动转化为工作台的直线运动.本文丝杠采用两端固定的支撑方式，固定端由一对背靠背的角接触球轴承支撑，左、右轴承座由螺栓紧固于底座.

图1 滚珠丝杠进给系统

1.2 轴向刚度和阻尼辨识模型

在建立滚珠丝杠进给系统轴向辨识模型时，主要考虑左、右轴承副和丝杠螺母副的轴向刚度和阻尼，忽略固定结合部的切向刚度和阻尼及伺服进给系统的扭转刚度和阻尼，将丝杠简化为弹性杆件.根据简化条件建立进给系统轴向力学模型，如图2所示.其中，k1和c1分别为左端轴承副的轴向刚度和阻尼；k2和c2分别为丝杠螺母副的轴向刚度和阻尼；k3和c3分别为右端轴承副的轴向刚度和阻尼；M为工作台的质量；丝杠左端为A点，丝杠右端为C点，丝杠螺母副中点位置为B点.

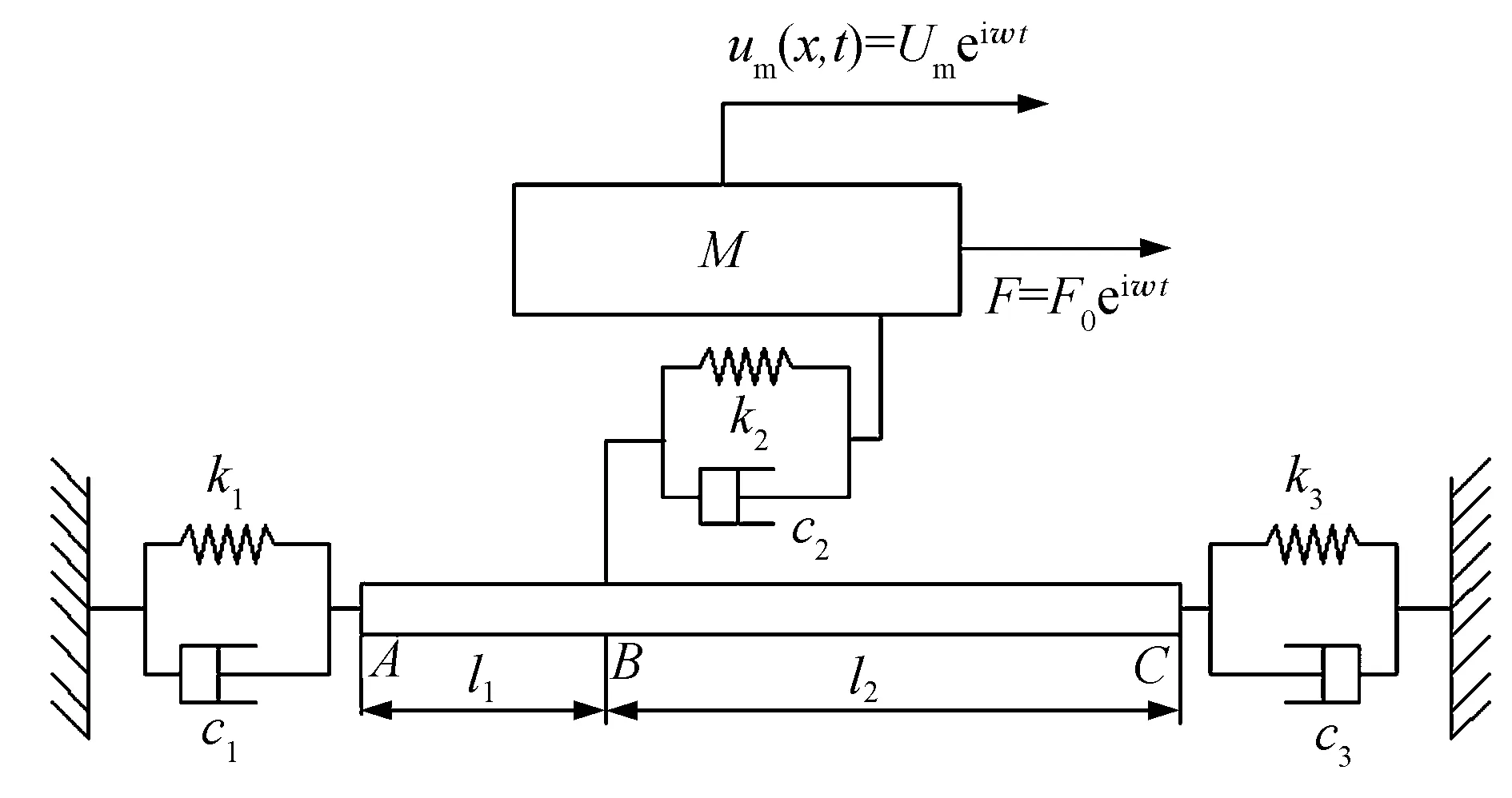
图2 进给系统轴向等效物理模型

给工作台施加激振力F=F0eiωt，其中，F0为幅值，ω为角频率，t为时间；则工作台发生简谐振动um=Umeiωt，其中，um为工作台的轴向振动位移，Um为um的幅值.假设丝杠上任意一点到A点的距离为x，则A点到B点的轴向振动方程为

(1)

式中:u(x,t)为丝杠在x处轴向振动位移；ES为抗压刚度；ρ为丝杠的线密度.

丝杠在简谐力作用下发生振动，故u(x,t)可表示为

u(x,t)=U(x)eiωt

(2)

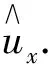
将式(2)带入式(1)可得：

(3)

式(3)的解可表示为

U(x)=C1sin(λx)+C2cos(λx)

(4)

式(4)也可表示为[12]

(5)

式中：UA为丝杠上A点轴向振动位移幅值;NA为A点轴向力幅值.

A点边界条件为

(6)

由式(3～6)可得:

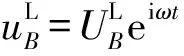
(9)

(10)

式(9)和式(10)可表示为

(11)

其中，

式(11)简记为

(14)

式中：

丝杠B点左、右两侧轴向受力模型如图3所示.

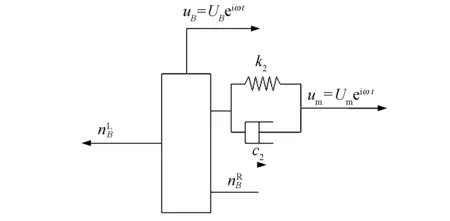
图3 B点左、右两侧受力分析

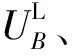
(15)

工作台的轴向受力模型如图4所示.工作台的轴向振动方程为

图4 工作台受力分析

(16)

由式(16)可得：

(17)

故式(15)可写为

(18)

式(18)简记为

(19)

式中：

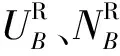
(20)

式(20)简记为

(21)

式中：

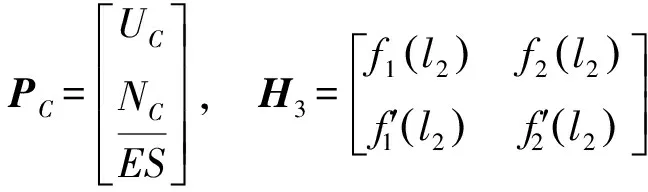
由式(14)、式(19)和式(21)可得：

PC=H1H2H3PA-H2Pf

(22)

(23)

则式(20)为

(24)

A点的边界条件为

(25)

C点的边界条件为

(26)

由式(24～26)可得：

由式(26)和式(27)可得：

UA=α/β

(29)

其中，

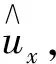
由于六元一次方程组求解较为困难，测量刚度、阻尼参数的次数一般大于6次，且为了减少测量误差对辨识结果的影响，所以采用优化算法求解方程组.设目标函数为

miny(φ),φ={k1,k2,k3,c1,c2,c3}

(32)

其中，

(33)

2 粒子群遗传混合算法

2.1 粒子群算法和遗传算法

粒子群算法是模拟鸟类觅食行为的群智能优化算法.在迭代过程中，粒子更新速度和位置分别为

vi,j(t+1)=ψvi,j(t)+φ1r1[pi,j-xi,j(t)]+

φ2r2[pi,j-xi,j(t)]

(34)

xi,j(t+1)=xi,j(t)+vi,j(t+1)

(35)

式中：i为当前粒子；j为当前维空间；ψ为速度的惯性权重；r1和r2为在[0,1]的两个随机数；φ1和φ2为学习因子；v为粒子的速度；p为粒子的最优位置.

粒子群算法流程如图5所示.

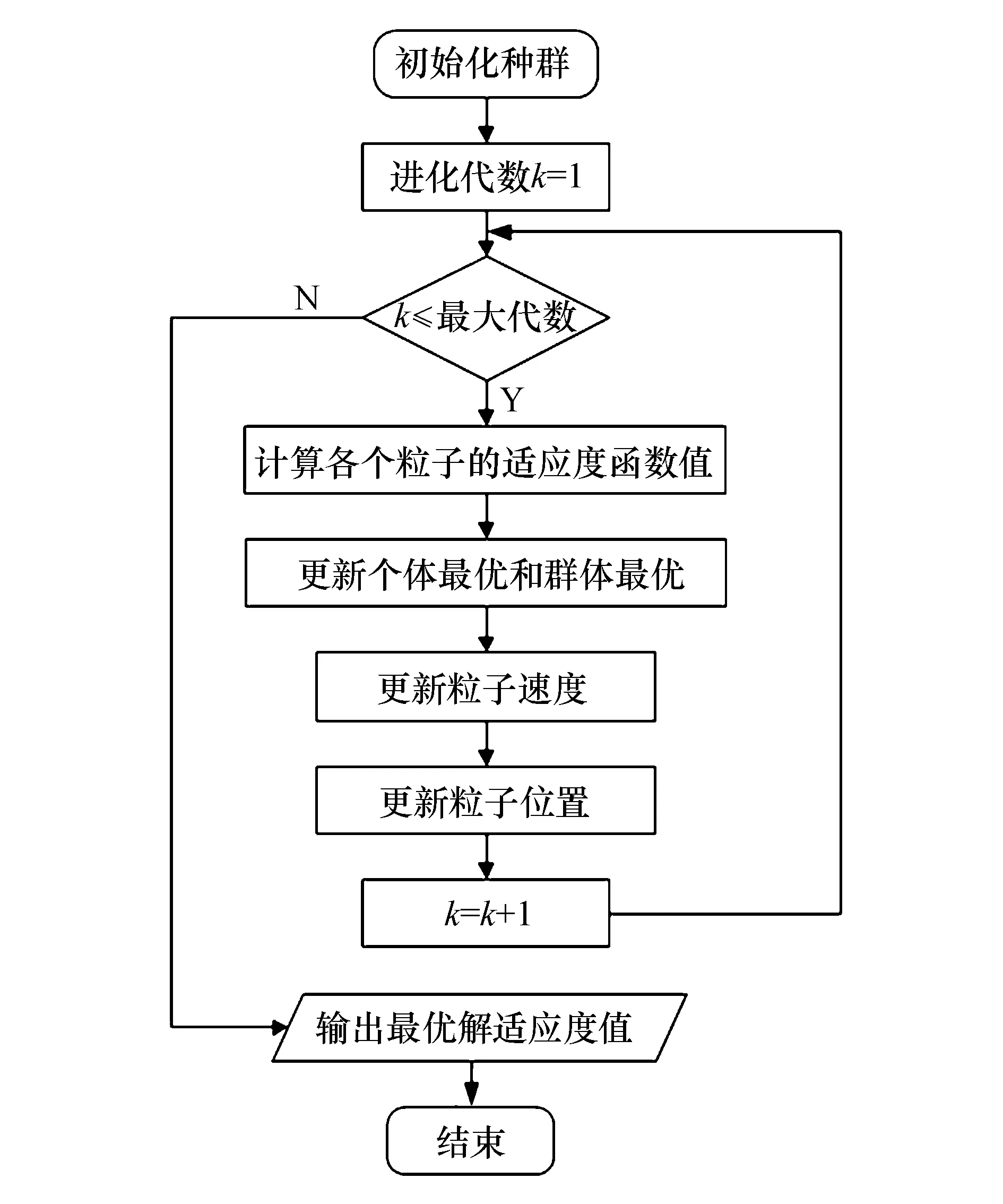
图5 粒子群算法流程图

遗传算法通过对染色体的选择、交叉和变异，仿效生物遗传过程中基因的重组、突变和变异3种方式.遗传算法流程如图6所示.

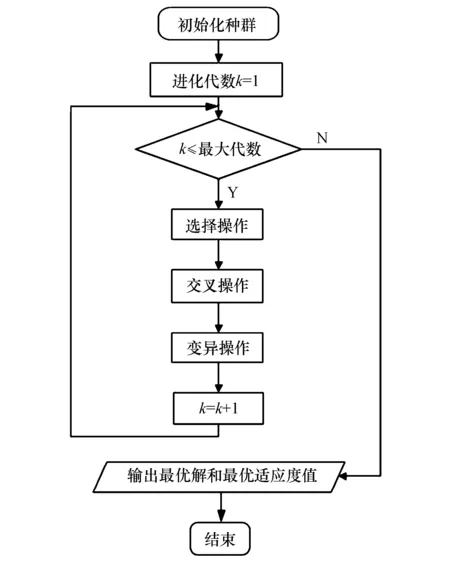
图6 遗传算法流程图

2.2 粒子群遗传混合算法

本文提出新的粒子群与遗传算法相结合的混合算法，原理如图7所示.该混合算法在初始化种群后，种群规模为N，将粒子群算法进化到T代.根据适应度函数值，将种群中适应度函数值优于种群平均值的个体Uk提取出来进入下一代，此时种群中剩余(N-Uk)个体.以剩余的(N-Uk)个体为基础，进行遗传算法进化，产生(N-Uk)个体.将剩余的(N-Uk)个体和遗传算法进化的(N-Uk)个体结合在一起后提取出前一半的(N-Uk)个体，再将粒子群进化得出的Uk个体和遗传算法进化得到的(N-Uk)个体结合形成新的粒子群种群N，之后进行下一步进化迭代.

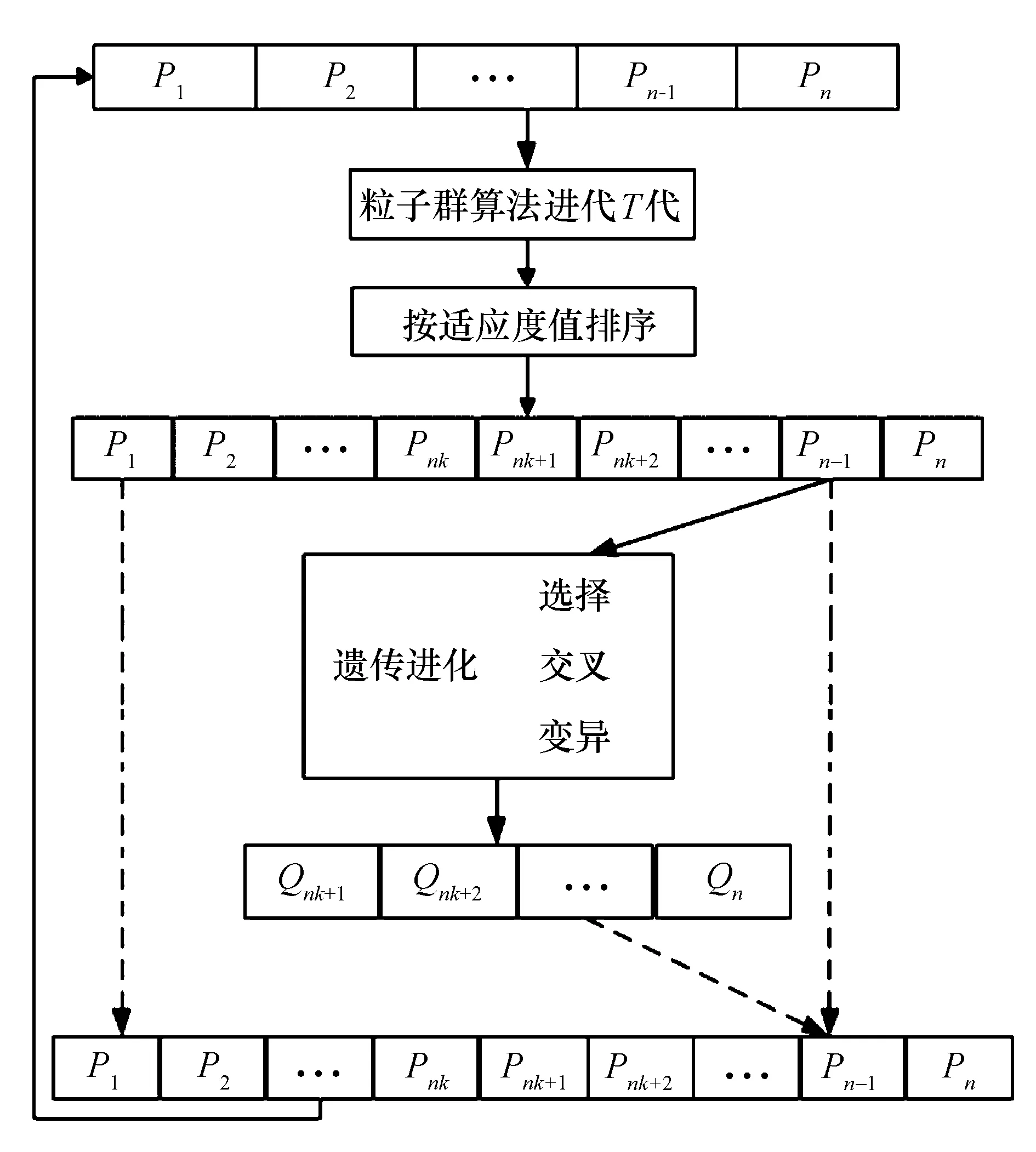
图7 粒子群遗传混合算法原理图

3 分析和讨论

本文为了准确获得滚珠丝杠进给系统结构参数，采用文献[13]的12组测量数据.当激振力的频率f确定为40.2 Hz时，工作台和滚珠丝杠基本参数如表1所列，粒子群遗传混合算法参数如表2所列,12组实验数据如表3所列.若无特殊说明，以下各算法均采用表2中的数值进行仿真分析.

表1 丝杠、工作台基本参数

将表3中的数据分别导入3种算法的MATLAB程序中，进行滚动结合部刚度和阻尼的辨识.分别运用遗传算法、粒子群算法、粒子群遗传混合算法对优化目标函数进行求解，确保各算法比较的有效性.各参数均采用表2中的数值，3种算法的迭代曲线如图8所示.从图8a可以看出，粒子群算法在迭代至第74代后几乎收敛，对应的种群目标函数最优值为0.721，且粒子数越大，种群越容易收敛到最优值.从图8b可以看出，遗传算法在迭代至第142代后收敛，对应的目标函数值为0.907.从图8c可以看出，混合算法在第1、22、46次迭代中种群最优值对应的目标函数值分别为83.420、1.324、0.570，该算法从第1次迭代到第22次迭代的收敛速度非常快，在第46次迭代中几乎收敛，对应的目标函数最小值为0.570.因此，混合算法的迭代次数相对较小，收敛速度较快，证明了本文混合算法的可行性.

图8 3种算法的迭代曲线

表2 粒子群遗传混合算法参数

表3 进给系统实验台的测量参数

刚度参数在第1、22、46次迭代中空间分布如图9所示，阻尼参数的分布类似于图9.从图9可以看出，第1次迭代的种群个体是随机分布的，在第46次迭代中种群个体收敛到最佳解，剩余的个体是由算法的不稳定性所造成.

图9 刚度参数散点分布图

经过多次运行求解程序，目标函数值为0.570对应的所识别参数如表4所列.可以看出，左轴承副的刚度参数与右轴承副的基本相同，但阻尼参数有所不同，主要在于左、右轴承副的预紧力、轴承间隙、润滑状态和外界温度等因素.

将表4中识别出的结合部轴向动态特性参数代入辨识模型，计算轴向振动幅值，并与文献[13]的实验结果相比较，如表5所列.可以看出，运用辨识模型计算所得理论振幅与实验所得振幅非常接近，最大误差为2.56%.从而验证了本文理论结果和辨识方法正确、有效，达到了较高的辨识精度.

表4 轴向刚度参数、阻尼参数辨识结果

表5 实验结果和理论计算结果比较

本文将3种算法重复20次实验后取平均值进行对比,如表6所列.可以看出，粒子群遗传混合算法除了运行时间较长之外，其他各方面均表现出明显优势.因为该混合算法保证了搜索的充分随机性，尽可能地遍历未知的解空间，逃离局部最优解的陷进，向最优解有序、有效地收敛，避免非最优解对收敛过程的扰动，从而解决了另外2种算法的缺陷，为辨识滚珠丝杠进给系统动态特性参数提供有效、准确的新方法.

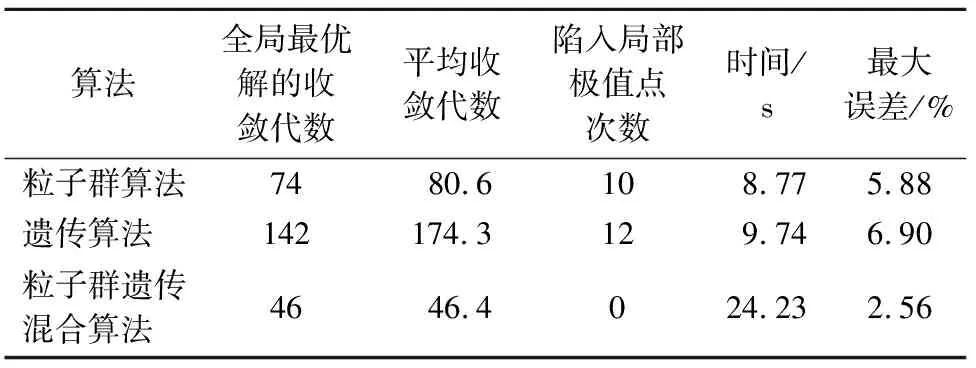
表6 3种算法性能比较

4 结论

1)本文提出了在装配状态下滚珠丝杠进给系统轴向动态特性参数的识别方法，将丝杠简化为弹性杆件，建立简谐激振力下丝杠和工作台的轴向振动方程，运用粒子群遗传混合算法识别出刚度参数和阻尼参数，结果表明该方法有较高的识别精度.

2)与遗传算法和粒子群算法进行了比较分析，仿真结果表明，粒子群遗传混合算法克服了易陷入局部最优的缺点，并且在收敛速度和陷入局部极值点次数两方面都有显著提高，为参数识别提供了新的方法.