矿用自卸车轮边减速器传动系统动态可靠性研究
尹煜鑫, 魏永峭*, 刘永平, 剡昌锋, 谢和平
(1.兰州理工大学 机电工程学院, 甘肃 兰州 730050; 2.徐州徐工矿山机械有限公司, 江苏 徐州 221004)
矿用自卸车轮毂驱动系统作为矿用自卸车的重要组成部分,其品质直接决定着整车的性能和可靠性;作为矿用自卸车轮毂驱动系统的核心部件,轮边减速器传动系统的可靠性亦成为制约矿用自卸车发展的重要因素,对其开展系统性的研究具有重要意义.矿用自卸车的工作环境恶劣、工况复杂多变,在低速重载的不断作用下,轮边减速器传动系统中齿轮易出现胶合、齿面折断等失效形式,导致系统可靠性偏低,难以实现系统的可靠性和寿命预测,致使目前我国工程机械大扭矩轮毂驱动系统完全依赖进口.因此,轮边减速器传动系统的可靠性研究成为亟待解决的问题.
针对齿轮箱传动系统可靠性分析,国内外许多学者进行了大量研究.吕媛波等[1]推导了基于疲劳损伤累积强度和总疲劳损伤量的齿轮接触可靠性公式,得到齿轮接触疲劳失效的极限状态方程,建立齿轮接触的疲劳可靠性计算模型.李铭等[2]利用最小次序统计量的概念建立齿轮的概率寿命预测模型,利用截尾误差对模型进行了验证.秦大同等[3]应用概率疲劳累计损伤理论,在考虑载荷参数随机的情况下建立了齿轮箱动力可靠度数学模型.林小燕等[4]在应力-强度干涉模型的基础上,推导出了齿轮传动动态可靠度函数.苏明明等[5]应用双参数Weibull分布描述随机载荷,依据Minner线性累积损伤理论对行星轮系进行疲劳寿命估算.Davide等[6]根据新型S-N曲线应用极大似然法对疲劳试验数据进行拟合,并将拟合数据与随机疲劳极限模型和双线性随机疲劳极限模型进行对比,验证曲线的可靠性.Popovic等[7]应用失效形式与影响分析方法(FMEA)对齿轮箱系统及其子系统的可靠性进行了分析.谢里阳[8]从可靠性角度出发,分析了齿轮传动系统载荷传递和失效的特点,以单级齿轮传动为例,建立不同系统结构参数、不同服役条件下的系统可靠性模型,展示系统可靠性变化规律.目前针对轮边减速器传动系统的可靠性研究还比较少,且研究只考虑单一因素对齿轮箱可靠性的影响.轮边减速器不断受到低速重载的作用,需要从材料强度退化与零部件失效相关性的角度考虑,对齿轮箱传动系统的动态可靠性进行分析.
齿轮材料的强度在载荷作用下总随着时间的推移发生不同程度退化.本文以电动轮矿用自卸车轮边减速器为研究对象,在考虑齿轮材料强度退化的基础上,从同一齿轮不同失效形式之间的相关性入手,采用Gamma随机过程对零件强度退化的随机性进行描述,建立零部件应力-强度干涉动态可靠度模型,利用Copula函数对系统疲劳寿命与各零部件疲劳寿命的关系进行研究,为轮边减速器传动系统的动态可靠性评估提供理论依据.
1 矿用自卸车受载状况分析
轮边减速器是矿用自卸车传动系统中唯一的减速增扭装置,其主要由齿轮、轴承和轴等基础件组成.由于行星轮系具有结构紧凑、承载能力大、传动比大、适用于低速大扭矩的传动装置等优点,所以矿用自卸车轮边减速器多采用行星轮系[9].齿轮箱可靠性分析中,轴、行星架、轴承等零部件可靠性较高.大量实际数据表明,在低速重载工况下矿用自卸车齿轮箱失效90%来源于齿轮失效.因此,齿轮作为减速器中易发生失效的零部件,其可靠性对传动系统的可靠性具有决定性影响.轮边减速器传动系统可简化为由各齿轮组成的串联系统,系统中任一单元发生失效都会导致整个系统失效.
本文矿用电动轮自卸车轮边减速器采用三级NGW行星轮系.其中,前两级为差动轮系,最后一级为行星轮系,结构简图如图1所示.轮边减速器在受到外部激励时三级行星轮系所受到的转矩相对于一、二级更大,可靠度最低.太阳轮在啮合过程中参与啮合频次最高,同等服役时间下太阳轮承受的载荷次数最多.因此,三级太阳轮最易发生失效[10].本文针对三级太阳轮失效过程进行研究,提出轮边减速器中齿轮可靠性研究的一般方法,进而对轮边减速器传动系统的可靠性展开研究.

r.输入轴;A1.一级太阳轮;A2.二级太阳轮;A3.三级太阳轮;B1.一级内齿圈;B2.二级内齿圈;B3.三级内齿圈;H1.一级行星架;H2.二级行星架;H3.三级行星架
矿用自卸车主要是将矿石从地势相对较低的矿坑运到地势相对较高处,矿车频繁上、下坡作业,最大坡度可达20°.在实际运行过程中,上坡时处于满载状况,且上坡工况在所有工况时长中占比最大[11].电动轮矿用自卸车在坡道上行驶时,作用于矿车上的阻力与驱动力保持平衡.车辆驱动力-阻力平衡方程为
Ft=Ff+Fw+Fi+Fj
(1)
式中:Ft为矿车驱动力;Ff为行驶时的滚动阻力;Fw为空气阻力;Fi为坡度阻力;Fj为加速阻力.
Weibull分布是描述机械系统及其零部件寿命分布规律最常用的分布形式之一.本文采用双参数Weibull分布来描述上坡工况时驱动力的规律[12],其概率密度函数为
(2)

2 考虑强度退化的可靠度计算方法
2.1 基于P-S-N曲线的强度退化随机模型
考虑到不同材料具有不同的性能,本文从P-S-N曲线入手研究特定工况下的材料性能,并结合Gamma过程建立强度退化随机模型.
Gamma分布的概率密度函数为
(3)

工程实践表明,材料的强度退化量随载荷加载次数的增加呈现上升趋势,但不会出现较大幅度的波动.因此,可以将Gamma过程看作稳定增长的过程.随着时间的增加,Gamma过程增量的数学期望和方差可视作线性增长,即
式中:E(t)为增量随时间变化的数学期望;Var(t)为增量随时间变化的方差;a为常系数.
P-S-N曲线能够反映材料的疲劳信息,在可靠性计算中用来描述不同存活率下的疲劳寿命.Gamma过程是随时间变化的随机过程,可将应力循环次数N看做时间t的函数,即
N=f(t)
(6)
通过对齿轮齿面接触疲劳强度进行修正,得到基于实际工况的齿面接触疲劳强度,即
(7)
式中:SH为齿面接触疲劳强度;ZN为接触强度寿命系数;ZL为润滑剂系数;ZV为速度系数;ZR为粗糙度系数;ZW为工作硬化系数;ZX为尺寸系数;C为材料实验常数.
通过对齿轮齿根弯曲疲劳强度进行修正,得到基于实际工况的齿根弯曲疲劳强度,即
(8)
式中:SF为齿根弯曲疲劳强度;YST为应力修正系数;YNT为弯曲强度寿命系数;YδrelT为相对齿根圆角的敏感系数;YRrelT为相对齿根表面的状况系数;YX为尺寸系数.
基于修正的疲劳强度计算公式,结合P-S-T曲线反映出的疲劳寿命信息,得到不同存活率下相同时间间隔[ti,ti+1]不同存活率的强度退化量Δrti.


2.2 齿轮动态可靠度计算
齿轮在疲劳载荷作用下通常具有齿面接触疲劳破坏和齿根弯曲疲劳破坏2种失效形式,并且分别对应2种失效形式下的强度初始值.
齿面接触疲劳强度初始值为
δH0=σHlimZNZLZVZRZWZX
(11)
式中:σHlim为齿面接触疲劳极限应力.
齿根弯曲疲劳强度初始值为
δF0=σFlimYSTYNTYδrelTYRrelTYX
(12)
式中:σFlim为齿根弯曲疲劳极限应力.
根据GB3480-1997轮边减速器太阳轮的切向载荷为
(13)
式中:nw为行星轮个数;ds为太阳轮分度圆直径;Ts为太阳轮转矩.
齿轮齿面接触疲劳随机应力σH和齿根弯曲疲劳随机应力σF分别为
式中:ZE为弹性系数;ZH为节点区域系数;Zε为重合度系数;Zβ为螺旋角系数;KA为使用系数;KV为动载荷系数;KHβ为接触应力计算齿向载荷分布系数;KHα为接触应力计算齿间载荷分布系数;d1为小齿轮分度圆直径;b为齿宽;KFβ为弯曲应力计算中齿向载荷分布系数;KFα为弯曲应力计算中齿间载荷分布系数系数;Yfα为齿形系数;Ysα为应力修正系数;Yε为弯曲应力计算中重合度系数;Yβ为弯曲应力计算中螺旋角系数;m为齿轮模数.
Monte Carlo模拟方法计算的收敛速度和误差大小与模型的复杂程度无关,被广泛应用在数值计算中,且模拟次数越多计算精度越高[14].根据应力-强度干涉模型,单一轮齿在随机载荷作用下考虑强度退化的应力-强度干涉动态可靠度模型为
R(t)=Pr[σ(t)<σ0-D(t)]
(16)
式中:R(t)为可靠度;σ(t)为应力;σ0为强度初始值;D(t)为强度退化量;Pr为可靠度运算符号.
3 基于失效相关性的可靠性分析方法
基于Monte Carlo模拟方法计算得到零件动态可靠度函数,再由零件可靠度函数与寿命分布函数之间的关系得到零件寿命分布函数[15].
假设齿面接触疲劳分布函数和齿根弯曲疲劳分布函数均服从于双参数Weibull分布,应用最小二乘法对寿命分布函数中的参数进行估计检验.为方便计算将双参数Weibull分布表达为
F(t)=1-exp[-tβ/θβ]
(17)
其中,θβ=φ,对两边取两次对数可得:
(18)
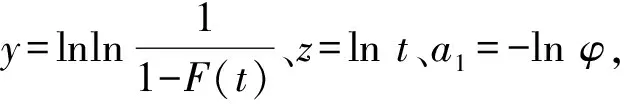
Copula函数本质上就是将联合分布函数和与其对应的边缘分布函数连接起来的函数,它能简洁明了地表达各个随机变量之间的函数关系[17].
Gumbel Copula函数属于3种常见的二元阿基米德Copula函数之一,其分布函数和概率密度函数分别为
(19)
(20)
式中:α为相关系数,且α∈(0,1],当α=1时随机变量独立,当α→0时随机变量趋近于完全相关.
Sklar通过定理的形式将多元分布函数与其低维边缘分布函数连接起来,避免了复杂的求解过程,为研究系统层面的可靠性提供了理论依据.
假设函数G(·,…,·)是具有边缘分布函数F1(·)、…、FN(·)的联合分布函数,则存在Copula函数满足:
(21)
轮边减速器由三级行星轮系组成,在求出各齿轮联合分布函数的基础上应用Sklar定理便可得到电动轮矿用自卸车轮边减速器传动系统的动态可靠度模型.
4 轮边减速器系统动态可靠性分析
本文矿用自卸车轮边减速器最大输出转矩为1.6×106N·m,减速比为62.43,齿轮材料均采用20CrMnTi渗氮淬火处理.减速器齿轮基本参数如表1所列.

表1 减速器齿轮基本参数
针对三级太阳轮,根据式(7)、式(8)分别计算相同时间间隔(10 000 h)内的齿面接触强度退化量及均值和方差的估计值,如表2、表3所列.

表2 不同存活率下相同时间间隔内齿面接触疲劳强度退化量

表3 相同时间间隔内齿面接触疲劳强度退化量均值与方差
基于表中数据,并根据式(9)、式(10)得到太阳轮齿面接触疲劳强度退化过程服从形状参数u=0.814 6、尺度参数v=0.001 3t的Gamma过程.同理可得,太阳轮齿根弯曲疲劳强度退化过程服从形状参数u=0.363 7、尺度参数v=0.001 3t的Gamma过程.
随着载荷加载时间的增加,太阳轮的强度退化量可以用相对应的Gamma过程来表示.应用统计学中的3σ原则,得到2种不同失效形式下强度退化量随时间变化的关系,如图2、图3所示,图中ΦD为强度退化量曲线.
根据图2、图3可知,太阳轮的强度退化量随着载荷作用时间的增加具有单调增长的趋势,其强度退化量在某一固定时间具有随机性,这也反映出材料的强度退化具有随机性和不可逆性两大基本特性.
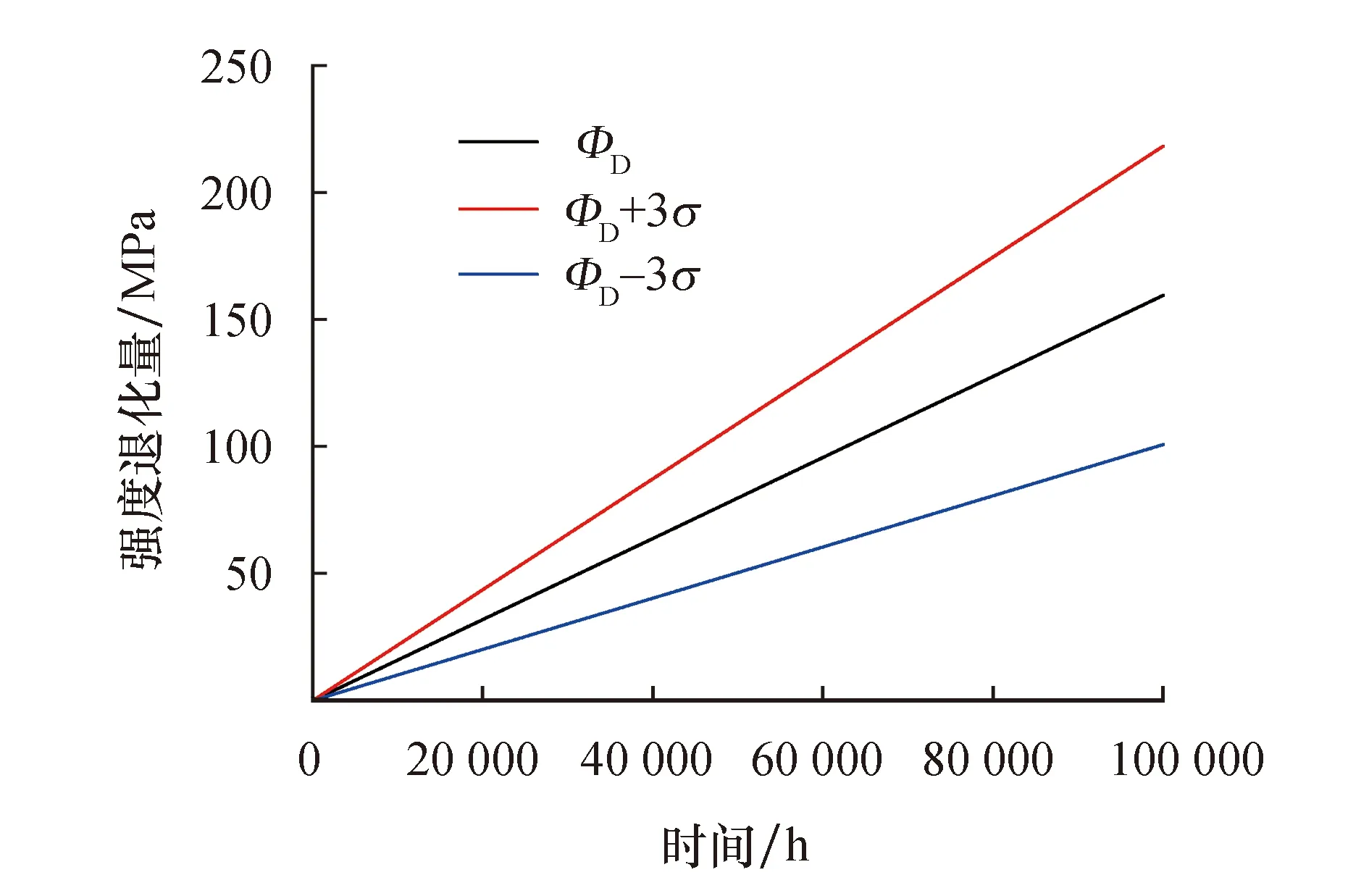
图2 齿面接触疲劳强度退化量
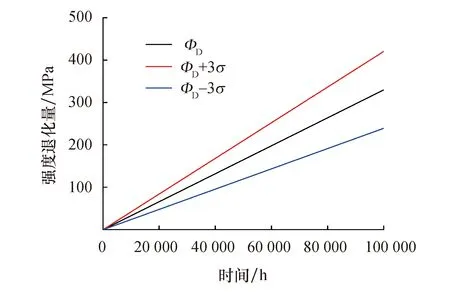
图3 齿根弯曲疲劳强度退化量
齿面接触疲劳强度初始值和齿根弯曲疲劳强度初始值的计算公式中各参数被认为服从正态分布[18],各参数的均值和方差如表4、表5所列.

表4 齿面接触强度计算式中各随机变量均值和方差

表5 齿根弯曲强度计算式中各随机变量均值和方差
根据已知参数的均值和方差可以确定太阳轮的初始强度值,进而确定三级太阳轮初始强度的变化曲线,如图4、图5所示.
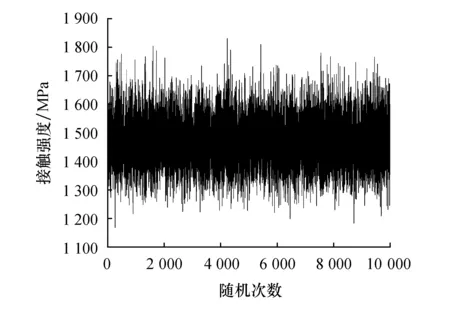
图4 齿面接触强度初始值

图5 齿根弯曲强度初始值
齿面接触疲劳强度初始值服从N(1 471,86.272)的正态分布,齿根弯曲疲劳强度初始值服从N(893.8,62.142)的正态分布.

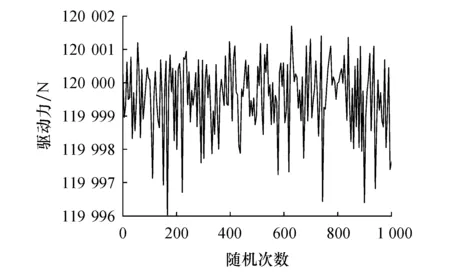
图6 驱动力时间历程

图7 转矩时间历程
驱动力时间历程服从β=36 988、θ=12 000的双参数Weibull分布,转矩时间历程服从β=113 791、θ=97 320的双参数Weibull分布.
三级太阳轮随机应力如图8、图9所示.齿面接触疲劳随机应力值服从N(1 169,50.032)的正态分布,齿根弯曲疲劳随机应力值服从N(229.7,16.262)的正态分布.

图8 齿面接触疲劳随机应力
在已知材料初始强度以及2种不同失效形式所对应的应力值和强度退化量的基础上,应用Monte Carlo方法计算得到齿轮2种不同失效形式下的动态可靠度曲线,如图10、图11所示.
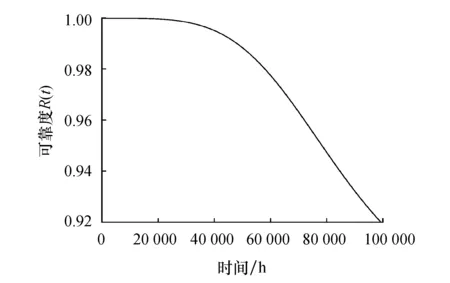
图10 齿面接触疲劳动态可靠度

图11 齿根弯曲疲劳动态可靠度
根据三级太阳轮齿轮不同失效形式下的动态可靠度曲线可知,行星轮系中太阳轮的弯曲疲劳可靠度相比接触疲劳可靠度要高得多,这说明行星轮系中太阳轮更加容易发生接触疲劳失效.但是无论何种失效形式下可靠度总随着时间的增加呈现稳定下降的趋势,且可靠度的下降具有不可逆性.
在已知可靠度曲线的前提下可以得到寿命分布函数随时间变化的曲线,如图12、图13所示.

图12 齿面接触疲劳分布函数

图13 齿根弯曲疲劳分布函数
从齿面接触疲劳分布函数曲线中抽取10个点,确定所对应10组ti和F(ti)的值,计算结果如表6所列.

表6 双参数Weibull分布的最小二乘法计算
根据表6的数据,应用最小二乘法计算得到参数a1=-28.827 5,a0=2.268 9,则φ1=3.304 8×1012,β1=2.268 9,相关系数γ1=0.994 6,相关系数趋近于1表明齿面接触疲劳分布函数服从双参数Weibull分布.齿根弯曲疲劳分布函数待估计参数φ2=1×1018,β2=2.967 9、相关系数γ2=0.997 5,同理齿根弯曲疲劳分布函数也服从双参数Weibull分布.
齿面接触疲劳分布函数和齿根弯曲疲劳分布函数分别为
应用最小二乘法对双参数Weibull分布的参数进行估计,并利用相关系数对估计结果进行检验,从而确定2种失效形式下的寿命分布函数均服从双参数Weibull分布.
在确定寿命分布函数服从双参数Weibull分布的基础上生成所对应的随机数,根据所生成的随机数绘制出联合寿命分布函数的二元频率直方图,如图14所示.

图14 不同失效形式下齿轮二元频率直方图
二元频率直方图反映出联合分布函数呈非对称性,其上尾部较高而下尾部较低.通过对比二元频率直方图与常见的Copula函数密度图,选择Gumbel Copula函数作为连接联合分布与边缘分布的工具函数.
在已知边缘分布函数和所选Gumbel Copula函数的基础上,对Copula函数中的未知参数α进行估计,得到三级太阳轮考虑失效相关性的Copula函数为
(24)
在确定动态模型的基础上得到三级太阳轮的动态可靠度曲线,如图15所示.

图15 三级太阳轮动态可靠度曲线
根据图15可知,随着载荷作用时间的增加三级太阳轮可靠度呈现降低的趋势,且在齿轮服役初期可靠度降低的趋势较为缓慢,但随着服役周期的增加可靠度迅速降低.这种趋势恰好反映了在考虑强度退化的前提下,齿轮材料的强度退化不断积累,导致三级太阳轮的可靠度下降趋势越来越快.
轮边减速器由三级行星轮系组成,在求出各齿轮联合分布函数的基础上,应用Sklar定理便可得到矿用自卸车轮边减速器传动系统的Copula函数,即
(25)
根据动态模型绘制出轮边减速器传动系统的动态可靠度曲线,如图16所示.
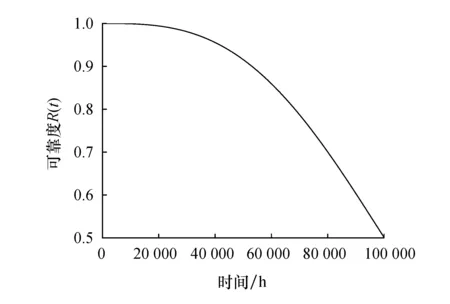
图16 轮边减速器动态可靠度曲线
根据图16可知,轮边减速器传动系统属于串联系统,其可靠度受到系统内各零件可靠度的影响,但总体变化趋势相对于单个零件的可靠度曲线不会出现太大变化.系统的动态可靠度曲线随着工作时间的增加同样也会出现稳定下降的趋势,且具有更快的下降趋势,可靠度数值相对于单个齿轮也有大幅减少.
在工程实践中,轮边减速器系统可靠度随着载荷作用时间的增加会呈现逐步下降的趋势.根据轮边减速器动态可靠度曲线所反映出的强度退化信息,在服役前期(40 000 h内)系统具有较高的可靠度,且系统可靠度下降的趋势较慢.随着服役周期的进一步延长,系统可靠度大幅度下降,此时应对系统进行妥善的维修与养护,确保轮边减速器能够高效、长时间地工作,提高系统运行可靠度.
5 结论
1)在考虑齿轮材料强度退化的前提下,根据Gamma函数和P-S-N曲线建立了不同失效形式下的强度退化随机模型,并且应用Monte Carlo模拟方法计算得到了考虑强度退化的单个齿轮齿面接触疲劳可靠度曲线和齿根弯曲疲劳可靠度曲线.
2)根据齿轮可靠度曲线,基于Weibull分布应用最小二乘法得到齿轮不同失效形式下的寿命分布函数.对比不同失效形式下的二元频率直方图,选择合适的Copula函数建立了考虑失效形式相关性的单一齿轮可靠度数学模型.
3)综合考虑系统零件失效形式的相关性,在构建各零件寿命的边缘分布函数基础上,引入Copula理论和Sklar定理对零件失效过程的相关性进行描述,揭示系统疲劳寿命与各零部件疲劳寿命之间的关系,建立了基于失效相关的系统疲劳寿命预测模型.掌握轮边减速器传动系统的动态可靠性评估和寿命预测技术可以提高系统寿命和可靠性,为轮边减速器传动系统的可靠性评估提供理论依据.

