液环真空泵吸排气段壳体型线耦合优化分析
张人会, 刘桂洪, 魏笑笑, 孟凡瑞
(1.兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2.兰州理工大学 甘肃省流体机械及系统重点实验室, 甘肃 兰州 730050; 3.淄博水环真空泵有限公司, 山东 淄博 255200)
液环泵属于抽送气体的流体机械,其工作原理类似于容积式泵,内部液环充当柔性活塞对气体进行抽吸和压缩.液环泵具备运行温度恒定、抽气量大等优点,因而被广泛应用于石化、电力、医疗等领域.但由于泵内具有复杂的气液两相流动,导致能量损失较大,性能提升困难.其中,壳体作为液环泵的重要组成部分,直接影响泵内工作介质的运动,对液环的形状起着限制作用.因此,合理设计壳体能够改善液环泵的水力性能.
国内外学者针对液环泵内部复杂的流动结构和性能优化分析已经做了大量的研究.在液环泵内部流动机理方面的研究包括:Raizmam等[1]通过探针测量的实验方法,对液环真空泵内部液环的速度场和不同径向截面的压力分布进行了研究;黄思等[2]和黄苗苗等[3]采用数值模拟对液环泵内部流场进行分析,得到了泵内两相流体的分界线、压力场、速度矢量等分布规律;张人会等[4,5]运用实验与数值模拟相结合的方法,分析了造成液环真空泵内部流动结构复杂的原因,并采用本征正交分解(POD)方法对泵内气液两相流场进行特征分解.在结构参数优化方面的研究包括:Teteryukov等[6]对液环泵壳体进行非圆柱形设计,并通过实验测试得到了适用于提高吸气量和真空度的壳体形状;任德高[7]、钟红华等[8]通过实验验证了液环泵的叶顶径向间隙对其性能的影响不可忽略;魏笑笑等[9]对叶片轴端开设射流孔,通过引入微射流来抑制液环泵轴端间隙泄漏流动对其水力性能的影响;张人会等[10]运用数值模拟分析了叶片型线和壳体与叶轮间的径向间隙对液环泵性能的影响;梁孟等[11]采用直接自由曲面变形参数化方法对液环真空泵吸气段壳体型线进行控制并优化;蒋利杰等[12]研究了液环压缩机排气口前端单向阀的开启对其性能的影响机理;赵万勇等[13]采用正交试验分析了液环真空泵叶轮各个参数对其性能的影响程度,并对叶轮进行优化设计.
目前关于液环泵非圆柱形壳体的设计理论和运用较少,且壳体型线对液环泵内部流动结构和性能的影响机理尚不清楚.因此,本研究综合考虑壳体型线的吸气段和排气段,运用响应面分析法结合NSGA-Ⅱ多目标优化方法实现壳体型线的优化,并对比分析优化模型与初始模型的内流场和外特性,为液环真空泵壳体型线的设计提供参考.
1 几何模型和壳体型线的参数化
1.1 几何模型
以2BEA-202型液环泵作为研究对象,将原有的双吸式改造成单吸式,其结构如图1所示,泵的主要几何参数如表1所列.

图1 液环泵的结构图

表1 液环泵的基本参数
1.2 液环泵壳体型线的参数化
直接自由曲面变形(DFFD)方法[14]是自由曲面变形(FFD)方法[15]的改进形式.DFFD方法具有算法稳定、局部变形能力强等优点,能够对需变形物体上点的位置进行直接控制,从而实现更精确、细致的参数化,在翼型的气动优化设计[16]中已得到广泛应用.
根据控制晶格点阵将需变形的壳体型线参数化表示为
(1)
式中:s、t、u分别为壳体型线上各点在控制晶格点阵中的相对坐标;Pi,j,k为控制晶格点坐标;Bil(s)、Bjm(t)、Bkn(u)为Bernstein基函数.
令Gf为目标点,Qf为壳体型线上原始点,其局部坐标为(sf,tf,uf).为使Qf变形得到Gf,控制晶格点阵需由Pi,j,k位移δi,j,k,因此Gf与Qf之间的关系可表示为

(2)
采用最小二乘法求解线性方程组,得到控制晶格点阵位移量δi,j,k,其表达式为

(3)
其中,
式中:hf为点Qf的局部坐标(sf,tf,uf).
为验证DFFD方法对壳体型线控制的可行性,选取壳体上4个点A、B、C、D作为直接控制点,如图2所示.首先将待变形的壳体嵌入控制框架中,构建方格网局部坐标系,获得壳体表面上各点在控制体中的局部坐标s、t、u;然后给定控制点B、D的径向位移量δ1、δ2,保持控制点A、C的位置不变,通过式(2)和式(3)可更新各控制晶格点的位置;最后由式(1)计算可得变形后的壳体型线.由图2可以看出,DFFD方法能够精确地控制壳体型线的变形量,且具有较好的局部变形和光滑特性.

图2 采用DFFD方法壳体型线变形前后对比
2 数值模拟和实验验证
2.1 三维建模和网格划分
整个计算域包括叶轮、壳体、吸气口和排气口4个部分,均采用Creo软件进行三维建模,如图3所示.对于不同的壳体型线,利用DFFD方法将变形后的壳体数据直接导入Creo中建模,有效缩短了建模时间.运用ICEM软件对计算域进行结构化网格划分,经过网格无关性检验,考虑到计算精度和成本,选取网格数约为170万.

图3 计算域网格划分
2.2 数值计算方法
采用Fluent对液环真空泵内部流动进行数值计算.由于泵内气液两相流动呈现分离状态,所以选取VOF两相流模型对泵内气液分界面进行追踪.采用RNGk-ε湍流模型,运用滑移网格处理壳体与叶轮之间的数据传递,边界条件选取质量流量进口和压力出口.按照理想条件下等厚度液环内表面近似与叶轮轮毂相切来计算初始液相区域面积,通过Patch命令给定泵内液相的初始区域.由于取样时间较短,暂不考虑由补液系统引起的泵内液量变化,所以液环泵进口为纯气相.时间步长取2×10-5s,当计算迭代步数为9 500步时,泵内流场数据基本稳定.为减小计算误差,总迭代步数取12 000步,采用最后1圈数据的平均值作为计算结果,即
(4)
式中:η为效率;P1为吸气口压力,Pa;P2为排气口压力,即大气压力,Pa;QV为进口气体体积流量,m3/h;M为扭矩,N·m;ω为角速度,rad/s.
2.3 实验验证
液环泵的性能测试系统如图4所示,主要由电动机、模型液环泵、进口管路、出口管路及补液管路组成.动力控制柜用于测量泵的输入功率.进口管路安装有调节阀、孔板流量计、真空表等,用于调节和测量进口气体流量和真空度.排气管路安装有出口单向阀、气液分离罐、压力表等.补液管路由调节阀和流量计等组成.

图4 实验测试系统
图5为液环真空泵实验与模拟结果的外特性曲线对比.可以看出,实验与数值模拟结果具有相同的变化趋势.由于未考虑系统泄漏和叶轮轴端间隙对液环真空泵性能的影响,所以模拟值的吸气压力(绝对压力)小于实验值,且随着流量增大和泄漏量增加,模拟值与实验值差距越加明显.理论上来说,数值计算具有较好的参考价值.
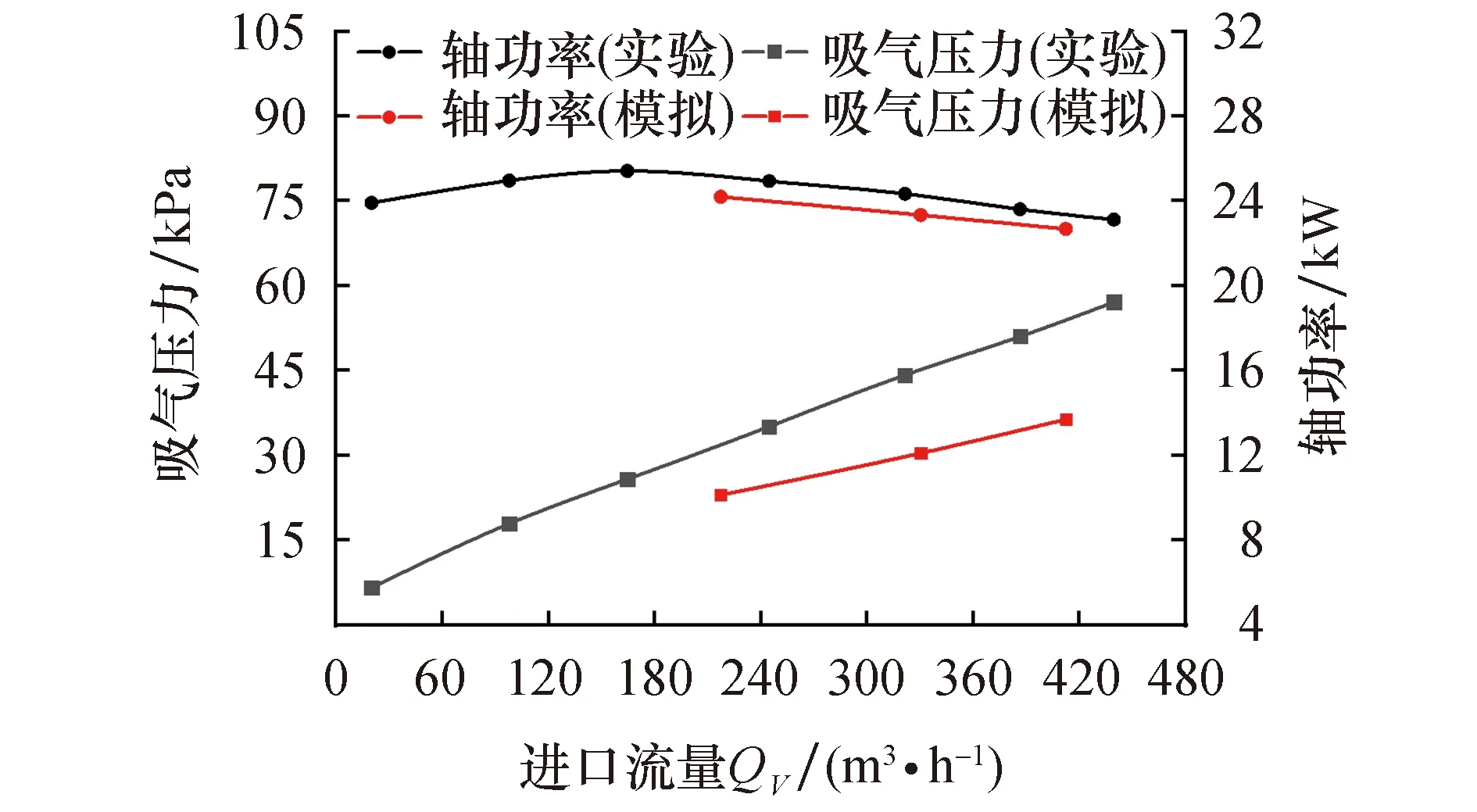
图5 液环泵数值模拟与实验结果对比
3 响应面优化实验和结果分析
3.1 壳体型线参数化变量
采用响应面方法(response surface methodology,RSM)[17]对液环真空泵吸气段和排气段壳体型线进行优化分析.通过DFFD方法对整个壳体型线进行参数化控制,将6个直接控制点A、B、C、D、P、N沿圆周方向均匀分布在壳体表面上,其角度位置如图6所示.由4个控制点A、B、C、D径向位置的变化计算各控制晶格点的新位置,从而更改壳体型线.点P、N在进行DFFD方法时作为固定点,以保证叶轮顶部与壳体的间隙和叶轮底部在液环中的淹没深度不变.
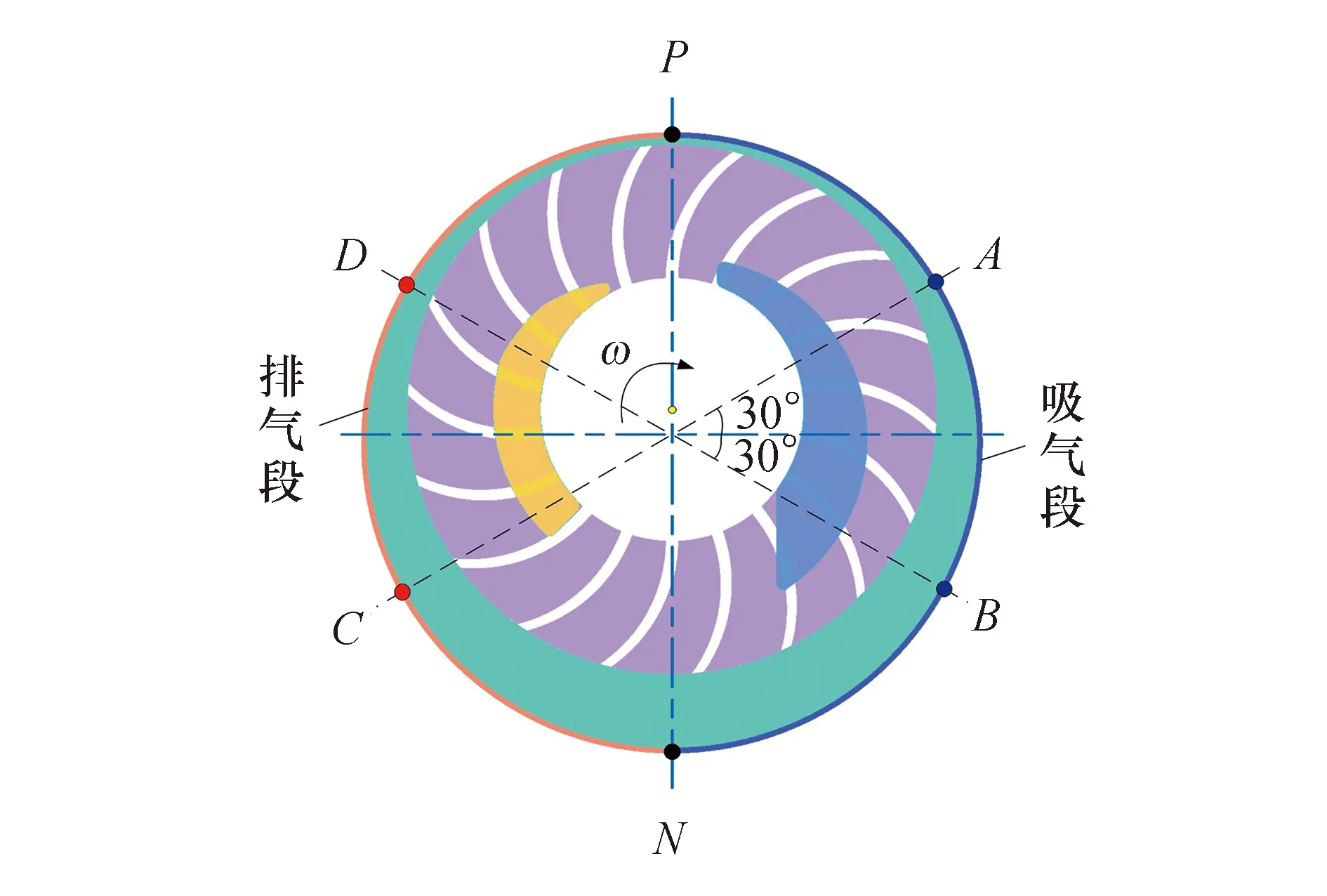
图6 壳体型线控制区域的划分
3.2 响应面实验设计
在响应面分析法中,常采用BBD(box-behnken design)和CCD(central composite design)2种实验设计方法.当因素相同时,BBD设计所需实验次数较少,且没有同时将所有因素安排为高水平的实验组合,适用于本研究中对吸、排气段壳体型线的优化分析.对筛选出的4个控制变量进行编码,如表2所列.根据BBD设计方法共进行26次测试,其中2个实验点为区域中心点.各个样本点的分布如图7所示.

表2 响应面因素水平

图7 各实验样本的分布
3.3 实验结果
在上述样本设计的基础上,由二阶多项式拟合可得液环泵进口真空度和效率关于壳体型线参数的响应面模型,如表3所列.其中,二阶多项式为
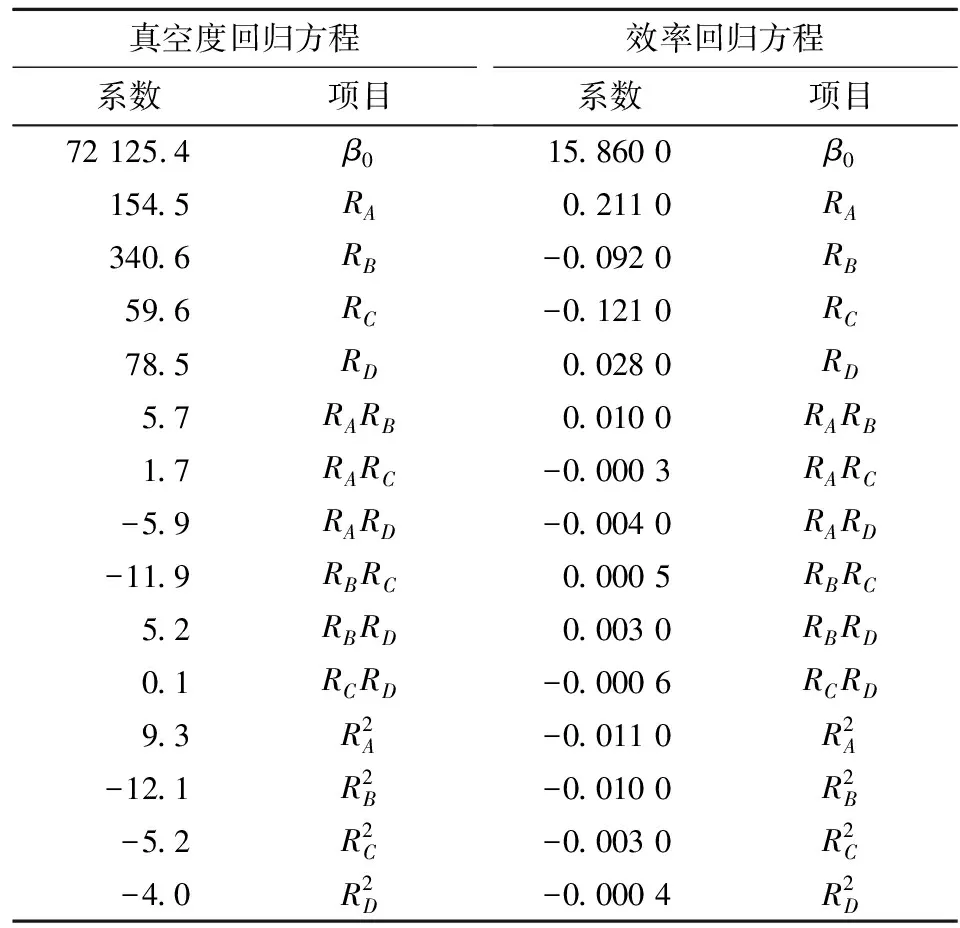
表3 真空度和效率的回归方程
(5)
式中:y(x)为响应目标;xi、xj为第i、j个实验因素;β0为常数项;βi、βii、βij为各项系数;m为因素个数.

3.4 目标函数的单因素响应
分析液环真空泵的性能随单个控制变量的变化规律,如图8所示.可以看出:泵的进口真空度随各个变量径向尺寸的增大而增大,其中RC、RD对真空度的影响较小,RB对真空度的影响最大;效率随着RA、RD的增大而增大,随着RB、RC的增大而减小,其中,RA对效率的影响最大,RD对效率的影响最小.

图8 目标函数随控制变量变化
3.5 控制变量的交互作用
为研究壳体型线的吸气段和排气段对液环真空泵性能的影响,采用交互作用分析,如图9所示.由图9a和图9b可以看出,液环泵的进口真空度随着吸气段(RA、RB)和排气段(RC、RD)径向尺寸的增大而增大,但吸气段对真空度的影响明显大于排气段,在排气段的等高线具有较大曲率,说明RC、RD交互作用显著;由图9c可以看出,效率随着吸气段RA的增大而增大,随着RB的增大而先增大后减小,交互作用显著;由图9d可以看出,效率随着排气段RC的减小而明显增大,随着RD的增大而缓慢增大.整体而言,吸气段壳体型线对液环真空泵性能的影响较排气段壳体型线更为显著,在进行壳体优化设计时,需对吸气段和排气段壳体型线进行耦合分析.

图9 控制变量的交互作用分析
4 液环真空泵壳体型线的优化
4.1 壳体型线的NSGA-Ⅱ多目标优化
采用NSGA-Ⅱ多目标优化方法[18]进行液环真空泵壳体型线的优化分析.选取效率和真空度作为优化目标,以上述构建的液环泵效率和真空度响应模型作为多目标优化过程中子代样本适应度的预测模型,交叉遗传概率设置为0.9,变异概率设置为0.1.经过300代的演化,得到真空度和效率的Pareto前沿,如图10所示.
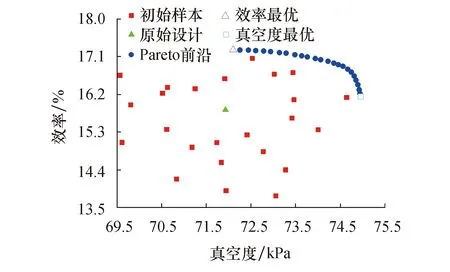
图10 液环泵壳体的NSGA-Ⅱ多目标优化结果
在Pareto前沿解中选取真空度最优点J和效率最优点K进行模拟验证,如表4所列,预测值与模拟值误差较小.将优化模型与初始模型进行性能对比,可以看出,优化模型的性能整体大于初始模型,如图11所示.优化模型J的真空度在各流量下分别较初始模型提高了2.9%、4.5%、3.9%.优化模型K的效率在各流量下分别较初始模型提高了0.9%、1.3%、0.9%.
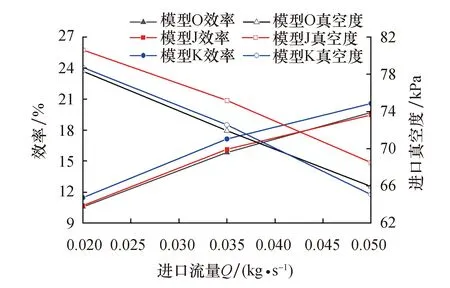
图11 优化模型与初始模型性能对比
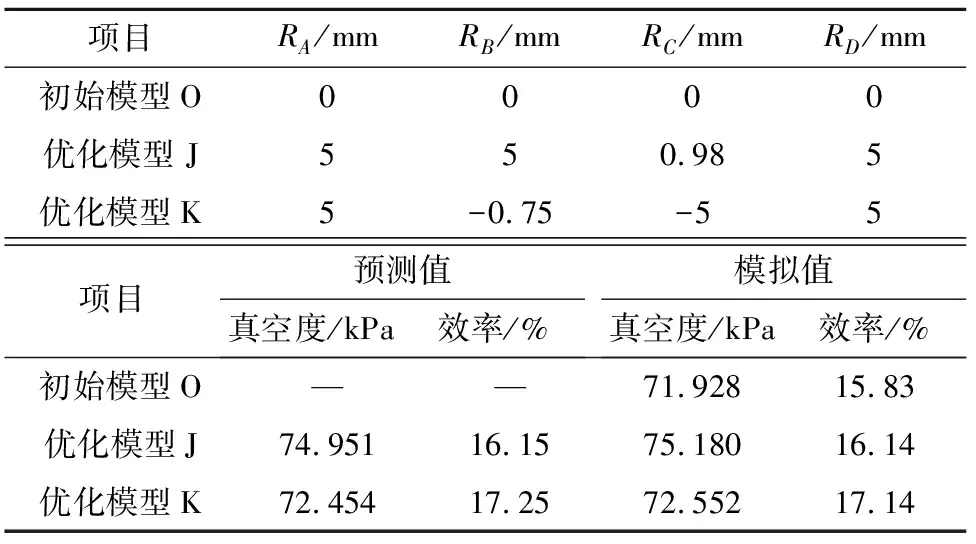
表4 NSGA-Ⅱ优化后的样本点
4.2 优化模型内流场分析
图12为优化模型与初始模型壳体型线对比.可以看出:真空度最优壳体型线较初始壳体型线整体向外扩大,吸气段RA、RB的增大有助于液环与叶轮间的小空间容积增加,液环泵的进口真空度随着吸气区流道面积比的增大而增大,与其工作原理一致;效率最优壳体型线的吸气段RA取高水平,RB与零水平接近,这样不仅保证了进口真空度,还有利于降低吸气区流道面积的扩散比,减少气体的扩散损失;效率最优壳体型线的排气段RC取低水平,RD取高水平,降低了排气区流道面积的收缩率,且能够提前压缩气体,使气体在排气口时达到排气压力,提高排气效率.
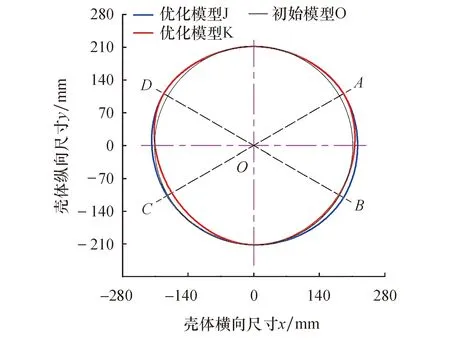
图12 优化模型与初始模型壳体型线对比
对比分析不同壳体模型叶轮内的压力分布如图13所示.由图13a可以看出,排气口始端位置的气体压力略低于出口压力(相对压力0 Pa),随着叶轮的旋转,气体进一步被压缩,直至达到排气压力条件;由图13b可以看出,吸气区气体压力在3个模型中最低;由图13c可以看出,排气段压缩区(RC)的壳体型线半径较小,因而排气口始端位置气体已经达到排气压力,有利于气体充分排出,进口真空度也稍高于原始模型,但低于优化模型J.
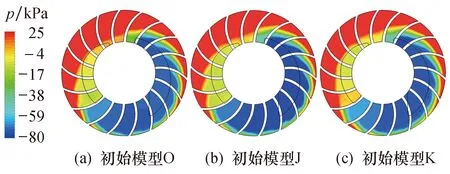
图13 不同模型叶轮内的压力分布
为研究壳体型线的变化对液环真空泵排气口回流的影响,取半径r=100 mm处的排气口区域圆柱面进行分析,如图14所示.其中,右边为排气口始端,左边为排气口末端.由图14a可以看出,初始模型泵出口的压力大于排气口始端,导致在排气口始端位置产生较大的回流;由图14b可以看出,优化模型J在排气口区域的回流有所降低;由图14c可以看出,因为优化模型K在排气口始端的气体压力已经达到排气压力条件,所以气体能够顺利排出泵外,极大地减小了回流,提高了排气效率.

图14 不同模型排气口的速度流线分布
5 结论
1)通过响应面分析法得到的多参数回归模型高度显著,能够反映壳体型线的控制变量与液环真空泵性能之间的客观关系.采用单因素响应和交互作用分析,对比研究了壳体型线的吸气段与排气段.结果表明,壳体的各个区域对液环真空泵的进口真空度和效率都有显著影响,但吸气段壳体型线对性能的影响明显大于排气段.
2)通过NSGA-Ⅱ算法对液环泵壳体型线进行多目标优化分析,在Pareto前沿中选取真空度最优和效率最优的壳体几何参数进行模拟验证.结果显示,预测值与模拟值误差较小,真空度最优模型的真空度提高了4.5%,效率最优模型的效率提高了1.3%.
3)对优化模型的内流场进行分析,结果发现:具有较大径向尺寸的吸气段壳体型线有助于提高液环泵的进口真空度;吸气区流道面积扩散比和排气区流道面积收缩率越小,泵内水力损失越低,效率越高;排气段压缩区的壳体型线对排气口回流的影响较大,具有较小压缩区径向尺寸的壳体型线能够提升排气口压力,减少排气口回流,从而提升泵的效率.

