带有薛定谔项的分数阶基尔霍夫方程解的存在性研究

韩志玲，桑彦彬，于 雪

(中北大学 数学学院， 太原 030051)

0 引言

考虑如下分数阶基尔霍夫型问题：

(1)

(2)

通过使用变分方法，得到解的存在性和多重性。2021年，文献[2]利用不同的方法研究了基尔霍夫问题：

通过将其转化为一个关于(u,λ)的等价方程组来得到原方程解的存在性。

另一方面，关于带有临界指数的分数阶基尔霍夫问题，已有大量结论。文献[3]通过Nehari流形和纤维映射研究了下列方程，得到了该问题非平凡解的存在性和不存在性：

文献[4]证明了由非局部积分微分算子诱导的基尔霍夫问题非负解的存在性。文献[5]研究了具有临界指数的分数阶基尔霍夫方程，利用变分方法得到了正基态解的存在性。更多关于带有临界指数的分数阶薛定谔型问题的结果，可参见文献[6-10]。

受上述文献的启发，把文献[2]的整数阶基尔霍夫问题推广到带有薛定谔项的分数阶基尔霍夫问题中。目的是将基尔霍夫的非局部项和带u的薛定谔项分离，从而转化为等价的方程组，其中非线性项满足次临界增长、超线性条件，同时通过下控制函数的次数q的分类，最终建立方程(1)具有一个和2个非平凡解的存在性和不存在性。

证明方程(1)和方程组(2)等价性的方法与文献[11]类似，通过3步获得方程组(2)解的存在性。

首先，根据山路引理求解下列方程：

(3)

然后，当确定了u，立即可解出：

(4)

最后，借助于等价结果得出方程(1)解的存在性。

1 主要命题及定理

命题1方程(1)至少有一个非平凡解v∈Hs(RN)当且仅当方程组(2)至少有一个非平凡解(u,λ)∈Hs(RN)×R+。

假设f满足如下条件：

(H3) 当t→0时，f(t)=ο(t)。

应用命题1，可以证明下面的定理。

定理1若f满足条件(H1)—(H4)，则下面结论成立：

2 预备知识

在证明主要结果之前，给出一些有用的定义。分数阶Sobolev空间Ds,2(RN)定义如下：

定义范数：

引理1存在正常数α>0，ρ>0，对任意的u∈∂Bρ(0)，有I(u)≥α。

证明对任意的C∈R，利用Hölder不等式，有：

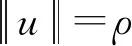
引理2存在e∈E，有I(e)<0。

φ′(t)=-qt-q-1F(tu)+t-quf(tu)=t-q-1(-qF(tu)+tuf(tu))≥0

因此，对任意的t≥1，有F(tu)≥tqF(u)。则：

因为q>2，所以当t→∞时，I(tu)→-∞，取e=tu，得到结论，引理2成立。

通过引理1和2，知道I具有山路几何结构，则定义I的山路水平集c为：

且Γ={τ∈C([0,1],E):τ(0)=0,I(τ(1))<0}。通过文献[12]中的定理3知道，I有一个(C)c序列。

为了得到方程(3)的非平凡解，在这一部分估计山路水平集c。

从文献[13]得到，在RN上，SN,s可由下列函数达到：

且

通过文献[14]中命题21和22，可得到：

(5)

(6)

(7)

(8)

上式表明2)成立。

因此完成证明。

3 (C)c序列

引理4令c∈R，{un}是I的(C)c序列，则{un}是有界的。

这表明在Hs(RN)中，{un}是有界的。

通过条件(H2)，有：

4 主要结果的证明

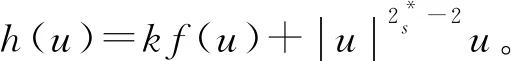
一方面，若方程(1)有解v∈Hs(RN)，则:

令

则：

h(v(y))=h(u(x))

因此，(u,λ)∈Hs(RN)×R+是方程组(2)的解。

另一方面，若方程组(2)有解(u,λ)∈Hs(RN)×R+,有：

(-Δ)su+u=h(u),x∈RN

和

(-Δ)su(y)+u(y)=h(u(y))=h(v(x))

因此，v∈Hs(RN)是方程(1)的解，证毕。

定理1的证明由命题1和文献[13]中的定理2.1和2.5，得到结论，证毕。

5 结论

对于带有薛定谔项的分数阶基尔霍夫型问题，即方程(1)，通过对N、q、a和b进行不同的限制，并使用山路引理，最终分别得到原方程有一个非平凡解、两个非平凡解和无解。