α-螺旋蛋白质中耦合非线性薛定谔方程高阶孤立波的动力学特性

商慧晶，宋 妮，张毅菲

(中北大学 数学学院， 太原 030051)

0 引言

1 耦合四阶非线性薛定谔方程

主要研究耦合非线性薛定谔(NLS)方程[14],该方程可以用来描述α-螺旋蛋白质的能量传递：

(1)

式中：qα(x，t)表示第α个脊柱激发的振幅；x表示距离；t表示延迟时间；*表示复共轭；γ表示高阶线性和非线性效应的强度。

基于方程(1),Sun等[15]通过符号计算和二元Bell多项式方法构造出该方程的双线性形式并研究了多孤子解；Du等[14,16]构造了广义Darboux变换,推导出该方程的一阶和二阶半有理解,并通过这些解对孤子、呼吸子和怪波进行分析,随后,又利用Darboux-dressing变换得到该方程的矢量怪波。

目前,对方程(1)四孤子相互作用的动力学特性的研究较少,因此,利用广义Darboux变换求得方程(1)的孤子解,通过数值模拟,进一步丰富了α-螺旋蛋白质中四孤子的动力学特性。

2 广义Darboux变换

方程(1)所对应的线性谱问题或Lax方程为：

Φx=UΦ

(2)

Φt=VΦ

(3)

其中：

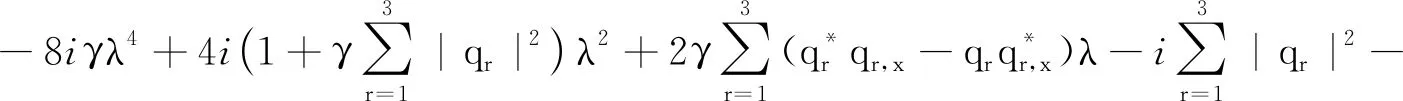
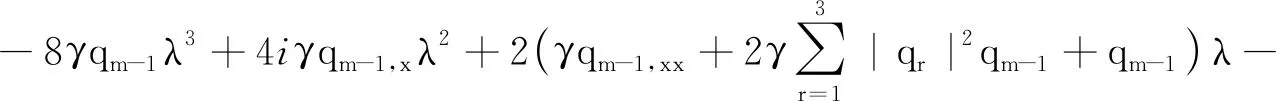
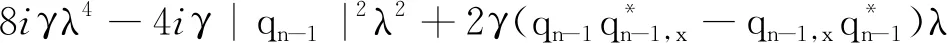
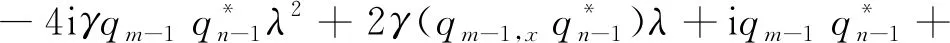
方程(1)可由相容性条件Ut-Vx+[U,V]=0得到,Φ=(φ,φ,χ,ψ)T是方程(2)和(3)的本征函数,λ是谱参数。

构造Darboux矩阵：

T[k]=λk+1I-H[k-1]Λ[k]H-1[k-1]

(4)

其中：

I为4×4的单位矩阵,Φk=(φk,φk,χk,ψk)T是方程(2)和(3)对应于谱参数λ=λk和种子解q1=q1[0]、q2=q2[0]和q3=q3[0]的本征函数。由Darboux矩阵T[k]得到方程(1)的Darboux变换：

ΦN[N-1]=T[N-1]T[N-2]…T[1]ΦN

(5)

(6)

(7)

(8)

基于上述经典Darboux变换,构造方程(1)的广义Darboux变换。假设Ψk=Φk[k-1]|λ=λk+η是方程(2)和(3)对应于谱参数λ=λk+η的一个特解,η=0是一个小参数,在η=0处对Ψk进行泰勒展开,得到：

(9)

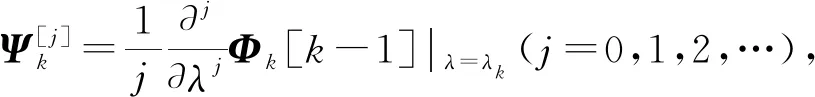
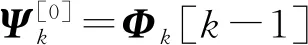
(10)

(11)

(12)

(13)

其中：

δk[N-1]=|φk[N-1]|2+|φk[N-1]|2+|χk[N-1]|2+|ψk[N-1]|2

Φk[N-1]=(φk[N-1],φk[N-1],χk[N-1],ψk[N-1])T

T[1]=I,T[k+N-2]=λkI-H[k+N-3]Λ[k]H-1[k+N-3]

3 四孤子的动力学特性

假设方程(1)的种子解为q1[0]=q2[0]=q3[0]=0,并将其代入方程(2)和(3)中,此时得到2个不同的基解矩阵：

其中Φa[0]、Φb[0]分别是方程(2)和(3)在λ=λ1、λ=λ2处的矢量解,sj1、sj2(j=1,2，…,4)是任意复参数,将Φa[0]和种子解q1[0]、q2[0]、q3[0]代入方程(5)—(8)中,得到方程(1)的一阶孤子解为：

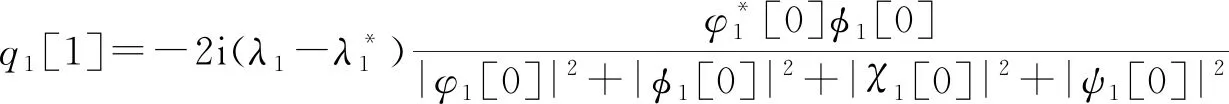
(14)

(15)

(16)

Φb[1]=T1[1]Φb[0]=Φb[0]

(17)

当Ψ2=Φb[1]|λ=λ2+η在η=0处对其进行泰勒展开时,可得：

(18)

由方程(10)—(13)分别得到方程(1)的二阶孤子解、三阶孤子解、四阶孤子解：

(19)

(20)

(21)

对于方程(1)的一阶、二阶、三阶孤子的动力学行为，Sun等[15]已研究过,这里不再赘述。接下来,通过选取合适的自由参数,分情况讨论四阶孤子的动力学特性。

1) 当Re(λ1)≠Re(λ2), Lm(λ1)=Lm(λ2)时,分量q1[4]、q2[4]和q3[4]中的四孤子相互作用，发生弹性碰撞,q3[4]中的孤子振幅最大,q1[4]中的孤子振幅次之,q2[4]中的孤子振幅最小,如图1所示。若其他参数不变,取s21=0,则各分量中的四孤子之间存在非弹性碰撞,q1[4]中的孤子相互作用后,其部分孤子发生退化,如图2所示。

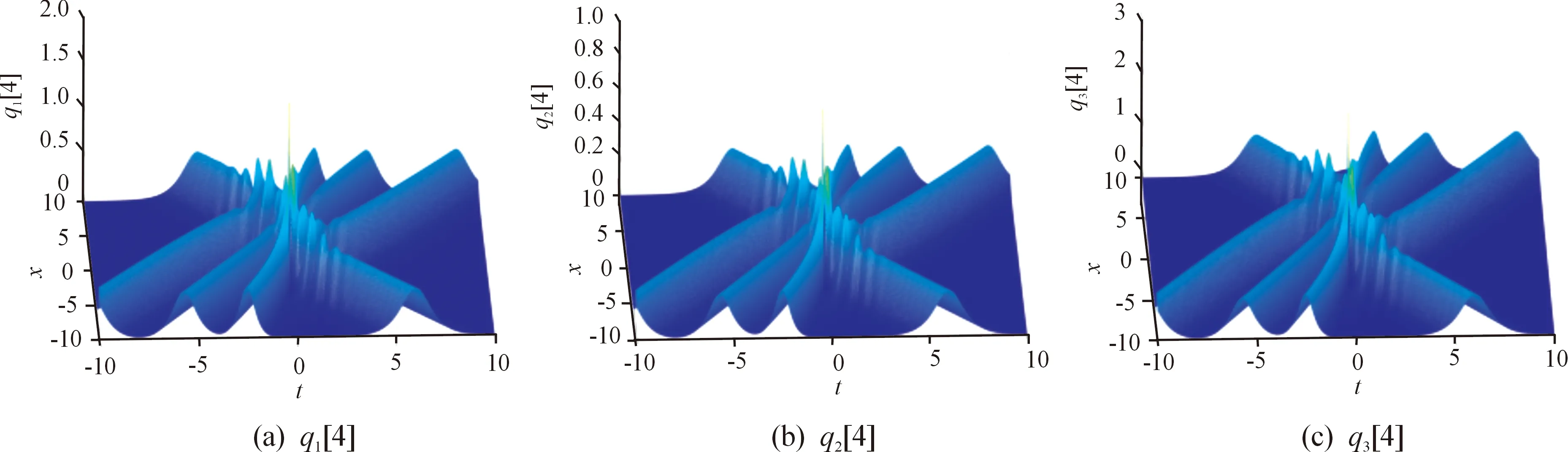
图1 当时,四阶孤子的动力学演化图

图2 当s21=0,其余参数与图1中的参数相同时,四阶孤子的动力学演化图

2) 当Re(λ1)=Re(λ2),Lm(λ1)≠Lm(λ2)时,又分为以下2种情况

若Re(λ1)=Re(λ2)≠0,q1[4]、q2[4]、q3[4]在相互作用的过程中发生了弹性碰撞,q1[4]、q2[4]、q3[4]的动力学特性基本保持一致,如图3所示。

图3 当时,四阶孤子的动力学演化图

若Re(λ1)=Re(λ2)=0,在相互作用的过程中,3个分量形成了一种束缚态,沿t轴方向在x=0处出现周期性的相互吸引与排斥,如图4所示。若其他参数不变,取s11=10,得到了不同形状的四孤子,其中q1[4]与q3[4]中孤子的振幅相同,q2[4]中孤子的振幅较大,如图5所示。若其他参数不变,取γ=2,与图4不同的是其束缚态的周期变小,峰数增加,如图6所示。

图4 当时,四阶孤子的动力学演化图

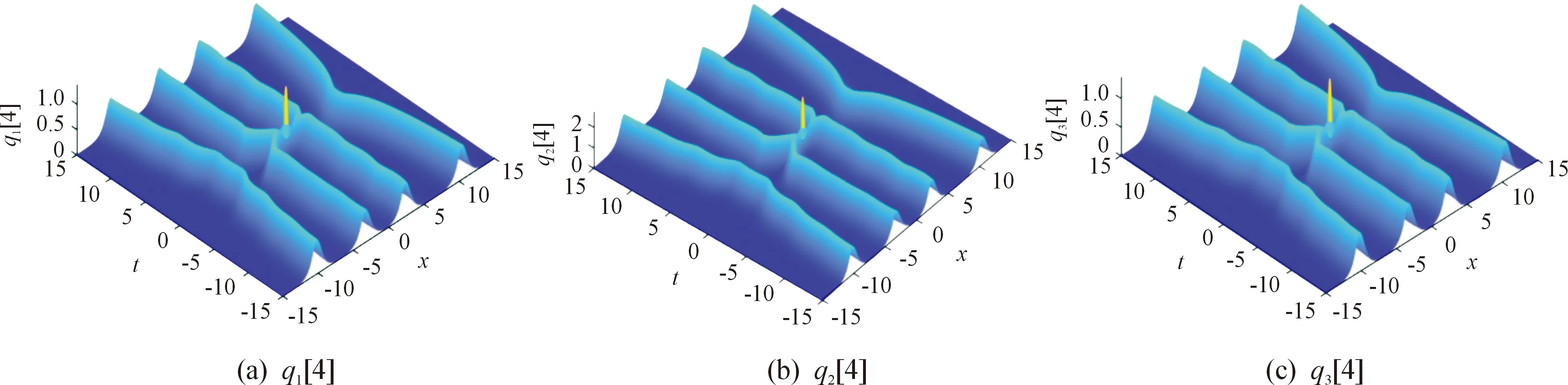
图5 当s11=10,其余参数与图4中的参数相同时,四阶孤子的动力学演化图

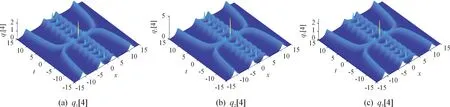
图6 当γ=2,其余参数与图4中的参数相同时,四阶孤子的动力学演化图

4 结论

利用广义Darboux变换,在零振幅背景下,对耦合非线性薛定谔方程进行求解,通过改变参数的取值,分析了孤子间相互作用的动力学特性,包括孤子的弹性碰撞、非弹性碰撞以及束缚态,所得结果在一定程度上有助于理解α-螺旋蛋白质中孤子的动力学特性。